铁路沿线地表条件与风沙流场的互馈规律研究

辛国伟，程建军，王　连，智凌岩，辛林桂

(石河子大学水利建筑工程学院，新疆石河子　832003)



铁路沿线地表条件与风沙流场的互馈规律研究

辛国伟，程建军，王连，智凌岩，辛林桂

(石河子大学水利建筑工程学院，新疆石河子832003)

为研究铁路沿线不同地表条件与挡沙墙周围风沙流场的互馈规律及挡沙墙挡风沙的功效，基于数值模拟及风洞实验，对不同地表粗糙度下的风沙流场进行数值分析，揭示地表粗糙度对流场表征量诸如风速、积沙形态的影响规律。结果表明：不同粗糙度下挡沙墙周围速度均形成减速区、涡流区与加速区，其中，加速区受粗糙度影响较大；粗糙度越大对近地表(1 m以下)速度削弱越大，但在1 m以上风速受其影响减弱；不同粗糙度下挡沙墙周围积沙分布不同，粗糙度越大，迎风侧积沙位移越长，风沙流饱和路径越小；随风速的增大，4类粗糙度下的积沙长度都表现为迎风侧减少，背风侧增多。

地表粗糙度；风沙两相流；挡沙墙；数值模拟；风洞实验

风沙运动是影响铁路运输安全的主要灾害之一。随着我国铁路运营速度的全面提升，风沙运动对列车安全运行的影响愈加突出，新建的兰新二线(百里风区)及青藏铁路(格拉段)面临的风沙灾害尤为严重。

为了保障列车的运输安全，目前国内对沙漠铁路沿线风沙灾害采取的防沙措施主要包括生物防沙及工程防沙。生物防沙可从根本上防治风沙灾害，但生物防沙体系的建立对当地水文地质条件有较高的要求，且需要一定的建设周期，而工程防沙体系的建立方便快捷，对自然环境要求较低，在大多数情况下是生物防沙不可或缺的辅助手段。工程防沙从其作用原理和功能划分，一般有固沙措施、阻沙措施、输沙措施及导沙措施。现阶段对上述两类防沙体系及防护效益的研究主要有现场勘测、风洞实验及数值模拟。现场勘测受场地局限、观测误差及风速不稳定等条件限制，不能准确摸清实际地形地貌条件下的风沙流特征，而风洞实验与数值模拟则主要集中在单风向定常风速、平坦地表等给定控制条件下沙粒输运、风场变化及其与挡沙墙相互作用的规律与特征，这使得现有的风沙运动理论、风洞实验及数值模型远未达到准确预测野外真实环境下挡沙墙周围风沙运动的程度[1-6]。实际环境中铁路沿线一般都是由沙丘、矮树丛及连绵山峦等地表障碍物组成的小尺度复杂地形，因此研究复杂地形下铁路沿线风沙流场的变化对预测野外真实环境下的风沙流运动具有重要的指导意义[7]。

为摸清铁路沿线地表条件对挡沙墙周围风沙流场变化规律的控制与影响，揭示地表条件与流场之间的映射关系，本文将现场实测、风洞实验及数值模拟相结合进行研究。其中，现场实测数据为入口风速条件，数值模拟为主要研究手段，风洞实验为验证手段。通过运用CFD计算程序设定平坦地表粗糙度，对挡沙墙周围的风沙流场特征进行数值分析，全面揭示地表条件控制下的风沙流规律，为后期沙害防治工程实践提供理论依据和参考。

1　实验设计

1.1风洞实验设计

风洞实验在中科院寒区旱区研究所风洞实验室进行。该风洞洞体全长38 m，实验段长21 m，风洞横断面为1.2 m×1.2 m；风洞由动力段、整流段、供沙装置、实验段和扩散段5部分组成。

实验模型为实体式挡沙墙，挡沙墙模型由PVC材料制作，模型高度H=20 cm，长度L=110 cm。对上述挡沙墙模型进行风洞实验：选取6、9、12、15 m/s 4组指示风速，使用皮托管分别测试挡沙墙迎风侧0.75H、1.5H、3H、5H及背风侧0.25H、0.5H、1H、2H、3H、5H、7H、10H处各高度的风速值。然后进行风沙流实验：在模型上风侧放置沙源，持续吹沙约1 min后，分别测试挡沙墙前、后的积沙范围以及积沙量。

因风洞实验装置因素，本实验只针对粗糙度为0.001(木板粗糙度约0.001)的下垫面进行实验。其实验布置示意如图1所示。

图1　风洞实验布置示意

1.2数值模拟设计

1.2.1模型建立

由AUTOCAD建立二维模型，CFD流体力学软件网格划分及数值模拟，TECPLOT进行后处理。计算区域长度120 m，高度30 m，挡沙墙高度2 m，宽度0.3 m。如图2所示。

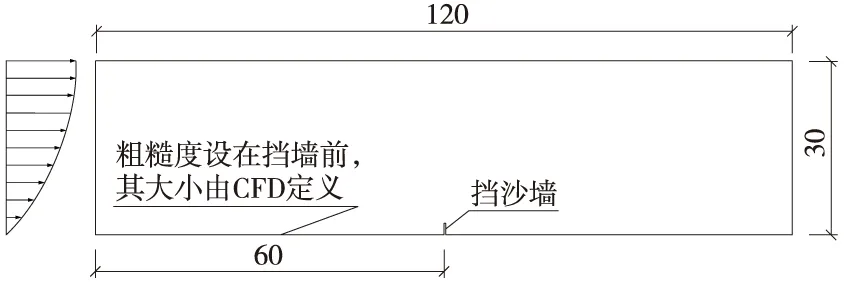
图2　计算区域示意(单位：m)

1.2.2网格划分

由于挡沙墙的存在，计算模型为不规则形状，故其网格划分类型采用Quad，即四边形网格形式，划分方法采用pave法(非结构化网格)，划分网格数约1.0×105个，并在挡沙墙周围进行网格加密，如图3所示。

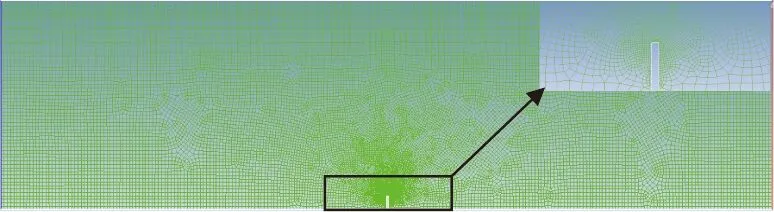
图3　网格划分示意

1.2.3边界条件

根据空气动力学原理，当马赫数小于0.3时空气流为不可压缩流，风沙两相流马赫数均小于0.3[8]，故计算模型入口条件为速度入口(VELOCITY-INLET)；自由出流必须在流态充分发展条件下才能采用，而此模型出口不能确保为自由出流，故模型出口条件为压力出口(PRESSURE-OUTLET)，其压差为零。挡沙墙前后壁面采用滑移壁面边界条件，其类型为WALL，粗糙度厚度值为Ks，其他壁面粗糙度默认为0。介质沙粒为连续相，其类型为FLUID。

1.2.4计算参数

风沙流携沙粒径一般在0.075～0.25 mm，本文风沙流携沙粒径ds=0.1 mm，沙粒密度ρs=2 600 kg·m-3，黏度μ=0.047 Pa·s，据统计风沙流密度的数量级在10-5(g·m-3)，且沙相为稀相，故初始沙相体积分数取为1%[9-11]。空气密度ρ=1.225 kg·m-3，黏度μ=1.789×10-5Pa·s，压力为常压；典型风速廓线为

式中，v为摩阻风速；k为冯卡门系数，取0.4；y0为粗糙长度；y为高度；v(y)为y高度处的风速值。

本文风速廓线通过实测数据进行拟合及推导，对比选取最优形式进行模拟。其实测数据在南疆铁路线吐鲁番至鱼儿沟段托克逊地区进行，设置数据测试点后用梯度风速仪测试测点各高度处的风速值，经处理后用Origin软件进行拟合[12]。推导通过测定任意两高度上风速获得摩阻风速并求取平均值，并由粗糙元平均高度H估算粗糙度长度y0=0.025，最终得出廓线方程[13]。不同高度风速拟合值、实测值及计算值对比显示拟合值更接近实测值，如图4所示，故选用拟合值作为本数值模拟入口的风速初始值。利用用户自定义函数(UDF)嵌入C语言自编函数，实现对数流入口边界条件的设定。

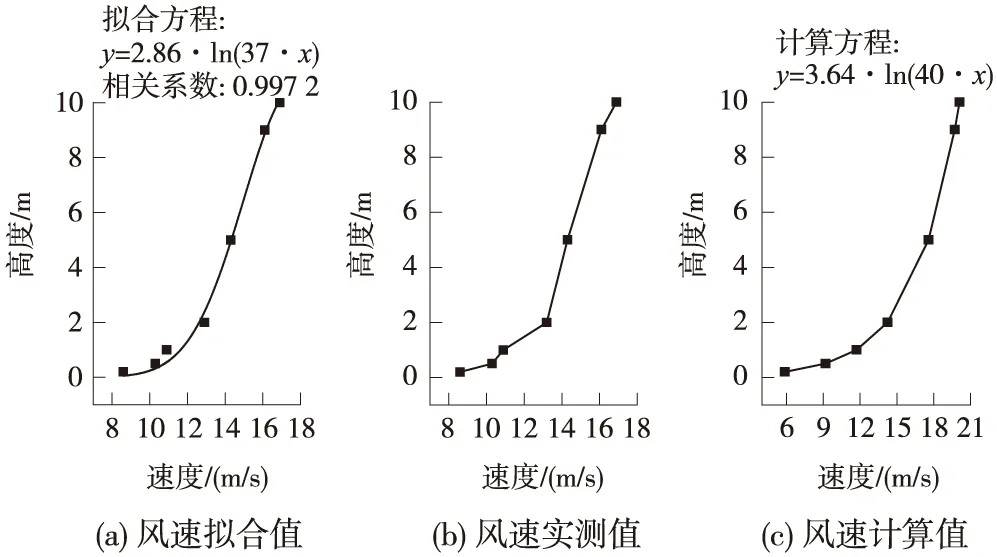
图4　不同高度风速拟合值、实测值及计算值对比

1.2.5求解模型

计算域求解模型采用欧拉双流体非定常模型，附加k-ε湍流模型，湍流强度I=0.05，湍流半径R=0.5，并选取Syamlal-O’Brien 曳力模型，两相流采用具有二阶截差的QUICK格式，以提高计算准确性。方程组求解计算方法采用SIMPLEC算法。

2　结果分析与讨论

2.1地表粗糙度对挡沙墙周围流场特征的影响

地表粗糙度(KS)是指近地表风速为零的高度，它是反映地表对风阻抗的重要参数[14]。防沙工程中常见的地表粗糙度如图5所示，不同地表粗糙度对风沙流的阻抗作用及挡沙墙防沙固沙效应不同，对挡沙墙前后积沙量及积沙长度的影响也不同。许多学者研究报道地表覆盖物或起伏地形能够增大地表粗糙度，以降低来流风速从而达到挡沙效果[15，16]。本文运用数值模拟的方式对4种固定规格的地表粗糙度(0.001，0.01，0.1，0.2 m)进行对比，以探究不同地表粗糙度对来流风速的减弱情况。其来流形式为对数流，初始速度大小为20 m/s(10 m高处)。

图5　不同类型地表粗糙度

地表粗糙度决定挡沙墙周围气流速度的大小，从而间接影响沙粒在挡沙墙周围的分布。以20 m/s为例模拟了4种粗糙度下的流场变化情况，其速度变化云图如图6所示。

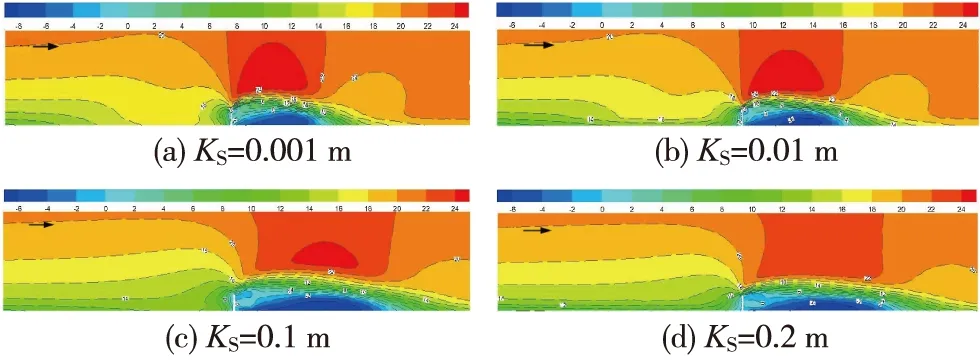
图6　不同粗糙度下挡沙墙周围流场速度分布云图

从图6可以发现，4种地表粗糙度下挡沙墙周围均形成速度分区：减速区、涡流区及加速区。速度分区的原因在于挡沙墙是一种带尖缘的钝体，风沙流经过时在其顶端部位受到了挤压从而产生了分离，形成一个强剪切层，剪切层两侧的压差使流线向下弯曲，而在气流接近地面时又返回了分离区，补偿了由于卷吸而带走的那部分气流，所以在挡沙墙背风侧形成一个很大的涡流区[17，18]。同时也可发现，不同地表粗糙度，对挡沙墙迎风侧速度削弱程度不同。粗糙度越大，对近地表风速的削弱越大(障前绿色部分)，风沙流到达沙障前速度变小，遇到挡沙墙后形成的速度分区也存在较明显的变化。从图6挡沙墙周围速度分区可以发现，4种粗糙度下，迎风侧减速区与背风侧涡流区(蓝色部分)变化大致一样，但斜上方形成的加速区范围却逐渐变小。说明地表粗糙度对减速区与涡流区影响较弱，但对加速区影响较大。产生此种变化的原因是远离近地表处速度较大，近地表风速较小且被削弱，在相同时间内上层气流运动路程比下层长，在遇到挡沙墙后近地表速度又急剧减小，上层气流与下层气流的速度差增大。粗糙度越大，下层气流速度被削弱越大，速度差越大。所以，地表粗糙度通过影响近地表风速间接影响挡沙墙周围的流场变化。

风沙流在入障前有一个减速区，其范围大于障前4H(H为挡沙墙高)。由图6可知，挡沙墙对其迎风侧0～10 m内风速有阻碍作用，而10～60 m范围内气流速度主要受沙粒及地表粗糙度影响。由于所取沙粒体积分数一定，所以在此范围内气流速度主要受地表粗糙度影响。障前10 m位置处速度变化情况如表1所示。从表1可以看出：在1 m高度范围内，随着粗糙度的增大，挡沙墙前速度呈递减规律，且递减程度增大；而在1.5 m及2 m高度处，随着粗糙度的增大速度呈递增规律，但递增程度减弱。其原因是粗糙度越大，出露在地表的零速度高度越大，对气流紊动性的影响程度加剧，对风速的阻力变大。此外，风沙流在距地表1 m范围内携沙量集中，沙粒运动对气流也有阻碍作用；而1 m以上受粗糙度影响减弱，对风速的阻力减小，携沙量也变小，使得速度逐渐沿对数曲线递增。图7为背风侧5 m处风洞实验与数值模拟速度对比示意。当地表粗糙度为0.001 m时，两者差距较小，误差不超过0.15[19](数值模拟速度值大于风洞实验值)。

表1　挡沙墙前10 m不同高度处气流速度变化

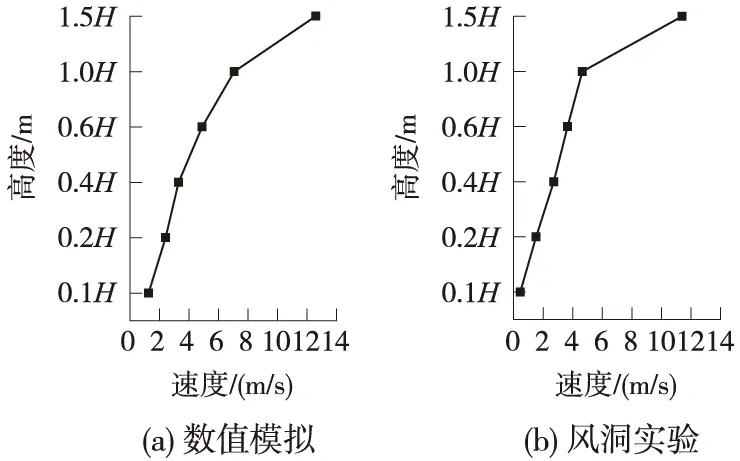
图7　数值模拟与风洞实验背风侧速度对比示意

2.2挡沙墙周围风速廓线的变化

风速廓线是表征近地表风速变化的基本方法，也是揭示风沙运动及风沙堆积的有效途径之一。一般情况下，风速廓线随高度的增加逐渐接近于某一固定值，但近地表由于受粗糙度影响速度递减，风速廓线会呈现出一定的变化。2 m高度范围内风速廓线变化如图8所示。由图8可知，风速廓线变化明显的区域主要在1 m以下，且越靠近挡沙墙，风速廓线转折段越明显；而在1 m以上范围内递增趋势逐渐变缓，有恢复至直线趋势。同时也可发现，随距挡沙墙距离的减小，风速廓线在近地表1 m以下位置递减幅度扩大，这与任春勇等人[20]的结论相一致。地表粗糙度对风速廓线的影响，实际上是下垫面状况对气流紊动性的影响，由于携沙气流的能量分布在垂直高度上变化很大，使得沙粒在风沙流活动层的高度分布受下垫面粗糙度的影响，最终导致近地表风沙流风速廓线的变化与净风条件下存在一定的区别。

2.3地表粗糙度对挡沙墙周围积沙分布的影响

风沙流运动过程中由于受地表粗糙度影响，运行速度减低，所携沙粒在遇到挡沙墙后大部分沉积挡沙墙周围。图9为15 m/s时不同地表粗糙度下的积沙分布图。从图中可以看出，粗糙度越大，对近地表气流速度的削弱越大，从而导致挡沙墙迎风侧积沙长度越长；同时还可发现，挡沙墙背风侧随粗糙度增大，其积沙量有减少趋势。其原因在于低风速(15 m/s)下，地表粗糙度较小时，迎风侧的速度虽有衰减，但仍大于起沙风速，风沙流仍处于欠饱和状态，部分沙粒仍可跃过挡沙墙在背风侧形成积沙；而地表粗糙度较大时，迎风侧速度被削弱较大，其风沙流可能处于饱和状态，在遇到挡沙墙后大部分沉落在迎风侧，仅有少部分沙粒可跃过挡沙墙在背风侧形成积沙。

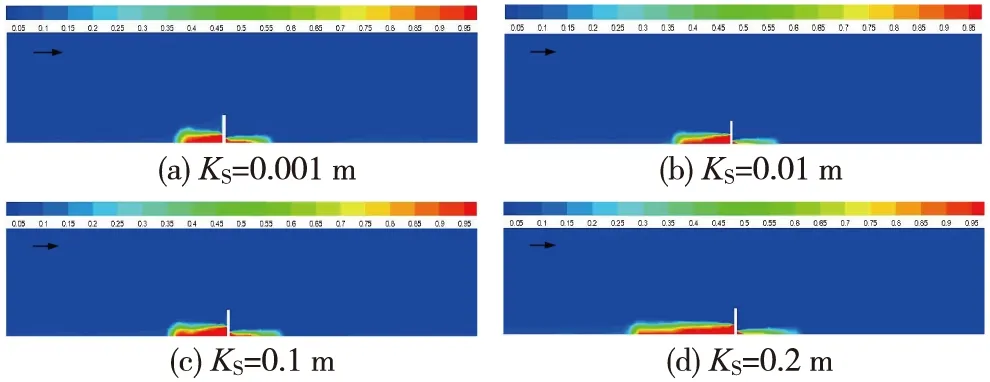
注：不同颜色代表积沙分布的多少，红色区域代表积沙最多，蓝色区域代表没有积沙，其他颜色代表沙粒还在运动。图9　不同地表粗糙度下的积沙分布

2.4风速对挡沙墙周围积沙分布的影响

风是沙粒运动的动力条件，当风速大于起沙风速时，沙粒开始移动；当风速不足以使沙粒移动时，大部分沙粒会在重力作用下沉积在地表面上。图10为不同风速(粗糙度0.001 m)下的积沙分布。从图中可发现，来流速度越大，挡沙墙迎风侧积沙减少，背风侧则表现出增大的趋势。这是由于挡沙墙聚风效应的影响，随着风速的增大，挡沙墙背风侧回流区范围变大，积沙区域也增大。图11为风洞实验积沙分布(风向从上到下)。从图可见，数值模拟与风洞实验结果基本吻合，由此说明模拟结果的准确性。

图10　不同风速时挡沙墙周围积沙分布

图11　风洞实验积沙分布

2.5地表粗糙度对风沙流饱和路径长度的影响

气流中的输沙量，从入口起点开始逐渐增加，当含沙量达到饱和时，就发生堆积。由入口起点到沙粒沉落堆积的一段距离称为饱和路径长度[21]。地表粗糙度对饱和路径长度有决定性影响，两者相关性如图12所示。由图12可知，随地表粗糙度增大，风沙流饱和路径长度逐渐减小，且其函数曲线呈指数规律。原因是地表粗糙度越大，气流运行速度受到的阻碍越大，附面层发生分离形成涡旋，降低近地面层的风速，从而削弱气流输沙的能量以及携沙的能力，使无力载运的沙粒跌落在挡沙墙附近，形成沙粒堆积。由此可见，在同一来流风速下，粗糙度越大，在挡沙墙前积沙的位移也越长。

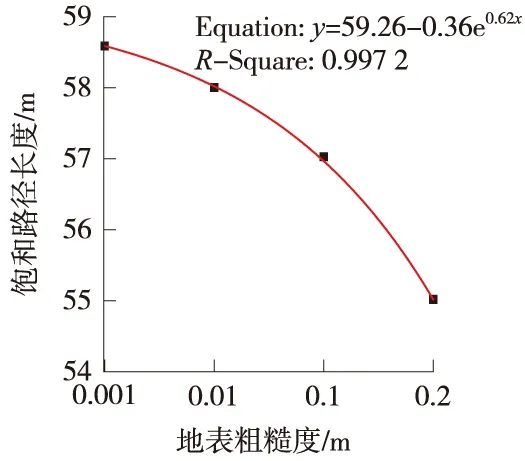
图12　不同地表粗糙度对饱和路径长度的影响

3　结论

本文基于欧拉双流体非定常模型，对不同地表粗糙度下的风沙两相流运动进行了数值模拟研究，得出以下结论。

(1)气流在挡沙墙周围均形成减速区、涡流区和加速区；减速区与涡流区受地表粗糙度的影响较弱，但加速区受其影响较大。

(2)不同地表粗糙度对近地表风速减弱程度不同。在1 m以下位置，粗糙度增大，对风速削弱程度加剧，离地表越近，削弱程度越大；而在1 m以上位置，粗糙度对风速影响减弱。

(3)4种地表粗糙度下积沙形态都表现为风速越大，挡沙墙迎风侧积沙越少，背风侧越多；不同地表粗糙度下，挡沙墙周围堆积沙的位移及形态随粗糙度增大表现出一定的递增性，但与风沙流饱和路径长度呈负相关。

[1]Cheng Jianjun， Xue Chunxiao. The sand-damage-prevention engineering system for the railway in the desert region of the Qinghai-Tibet plateau[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2014(125):30-37.

[2]Li Bailiang， Douglas J, Sherman. Aerodynamics and morphodynamics of sand fences: A review[J]. Aeolian Research， 2015(17):33-48.

[3]庞巧东，程建军，蒋富强，等.戈壁铁路挡风墙背风侧流场特征与挡风功效研究[J].铁道标准设计，2011(2):1-5.

[4]朱文智，程建军，张云鹏，等.土堤式挡风墙加高挡板稳定性分析及研究[J].铁道标准设计，2015，59(1):16-20.

[5]李凯崇，蒋富强，薛春晓，等.兰新铁路十三间房段的戈壁风沙流特征分析[J].铁道工程学报，2010(3):15-18.

[6]程建军，蒋富强，杨印海，等.戈壁铁路沿线风沙灾害特征与挡风沙措施及功效研究[J].中国铁道科学，2010(5):15-20.

[7]史锋，刘奇伟，黄宁.复杂地形下的近地层风沙运动模拟[J].计算力学学报，2008，25(S1):52-57.

[8]程建军，庞巧东.戈壁强风区挡风构筑物限制下列车气动力学特性分析[J].铁道标准设计，2013(1):1-4.

[9]程宏，邹学勇，张春来.摩阻风速与平均风速的转化关系研究[J].水土保持研究，2007，14(2):133-138.

[10]Zingg A W. Wind tunnel studies of the movement of sedimentary materials[C]∥Kansas America: Proceedings of the 5th Hydraulic Conference Bulleti， 1953:111-135.

[11]岳天祥，王薇，于强，等.中性条件下垂直风速廓线及其参数模拟分析[J].资源科学，2006，28(1):136-144.

[12]景文宏，程建军，蒋富强.轨枕式挡沙墙挡风沙功效的数值模拟及实验研究[J].铁道科学与工程学报，2016，13(1):181-189.

[13]Grimmond C S B， Oke T R. Aerodynamic properties of urban areas derived from analysis of surface form[J]. Journal of Applied Meteorology， 1999，38(9):1262-1292.

[14]周娜，张春来，邹学勇，等.地形对包兰铁路沙坡头段防护体系的影响[J].地理科学，2014，34(7):889-896.

[15]石雪峰.北方半干旱区风沙活动与植被条件的耦合关系[D].北京:中央民族大学，2005.

[16]李霞.农田带状间作留茬抗风蚀效应风洞模拟研究[D].呼和浩特:内蒙古农业大学，2006.

[17]庞巧东，刘建军，程建军，等.戈壁铁路挡风墙背风侧涡流长度及积沙的研究[J].石河子大学学报：自然科学版，2011，29(5):629-632.

[18]高永平，钱伟平.浅析兰新铁路防风工程[J].资源环境与工程，2009，23(9):48-51.

[19]张默.基于FLUENT的建筑物风沙两相流场 数值模拟[D].哈尔滨:哈尔滨工业大学，2008.

[20]任春勇.基于欧拉模型的风沙流运动模拟[D].兰州:兰州大学，2011.

[21]马高生.定常和非定常来流下的风沙流数值模拟[D].兰州:兰州大学，2011.

Research on the Law of Mutual Feedback between Ground Surface Condition and Wind-sand Field along the Railway

XIN Guo-wei， CHENG Jian-jun， WANG Lian， ZHI Ling-yan， XIN Lin-gui

(College of Water Resources and Architectural Engineering， Shihezi University， Shihezi 832003， China)

To understand the law of interaction between different ground surface conditions and the wind-sand field around the sand retaining wall and the effect of the sand retaining wall， different surface roughness of the wind-sand is analyzed based on numerical simulation and wind tunnel experiments to reveal the effect of ground surface roughness on such wind-sand field token states as wind speed and sand form. The results show that different surface roughness degrees all result in deceleration zone， vortex area and accelerating zone around the retaining wall， and the acceleration zone is much influenced by the roughness; the greater the roughness， the bigger the near surface (less than 1 m) deceleration， but the wind speed is less influenced above 1 m; the sand distribution is different around the retaining walls of different roughness; the greater the roughness， the longer the sand displacement on the windward side and the smaller the sand saturation and the flow path; with the increase of wind speed， the length of the sand deposition on the windward side decreases and that on the leeward side increases for all the four kinds of roughness．

Ground surface roughness; Wind-blown sand flow; Sand-retaining wall; Numerical simulation; Wind tunnel test

2016-01-09；

2016-03-13

国家自然科学基金项目(51568057；51268050；50908152)

辛国伟(1990—)，男，硕士研究生，E-mail:942974011@qq.com。

程建军(1979—)，男，教授，工学博士，从事铁路风沙防治研究，E-mail:chengdesign@163.com。

1004-2954(2016)09-0022-06

U216.41+3

ADOI:10.13238/j.issn.1004-2954.2016.09.005