有趣的海盗博弈难题

王天琦

【摘要】在学习博弈论的过程中，笔者发现与其他经济学理论一样，博弈论也越来越依赖于数学模型，但对高等数学的应用又不够严谨。本文将通过探讨一个有趣的博弈模型：海盗博弈，向大家展示一个小参数的变动，也可能使模型结果产生颠覆性的改变。盲目的应用数学，即使大师的结论也不一定准确。模型的变动集中在投票比例的优化上，我们仅将海盗博弈模型的投票比例调整为“三分之二多数”，得出的结果就与权威结论相反了。本文希望借此提醒读者：面对以往的结论不要盲目轻信，对待自己即将提出的理论也要深思熟虑在发表出来。开阔思路，不断创新才是社会发展的动力源泉。

【关键词】博弈论 海盗博弈 数学模型 投票模型

在博弈论和数学领域，一直流传着一个经典的海盗博弈难题：5名海盗找到了100块金子，需要分配。这些理性的海盗按下面的方式分配：最强的海盗提出分配方案，所有的海盗投票决定是否接受（包括提出方案者本人）。如果50%以上的海盗赞同此方案，那么提议通过。在只有一半人同意的情况下，提议者拥有决定权。如果没有通过，那么提议人将被扔出船外，然后下一名最强的海盗提出新方案。海盗们基于三个因素来做决定：第一，自己活下来。第二，得到的金子最多。第三，在其他条件相同的情况下，优先把别人扔出船外。那么最强的海盗最多能得到多少金块？

研究这个模型的人很多，题本身也有不少版本，最重要的是华威大学的史都华教授。他将海盗博弈模型推广至无穷，发表在《科学美国人》上，并得出了有趣的结论：“由于这些海盗所实行的那种民主制度，他们的事情就成了最强的一批海盗多半都是下海喂鱼……只有最弱的200名海盗有可能分得一份脏物，而他们之中又只有一半的人能真正得到一块金子，的确是若者继承财富。”我们简单介绍一下他的思路：

首先我们把海盗按照实力逆序编号（1号最弱），然后从只有两名海盗的情况逆推（这是解题关键）。只有两个人时，2号的任何提议自己都会同意，这时他就有了一半的票数，而且又有决定权（即使按照实力来讲，他也足以仗势欺人），所以任何议案都会通过。他的选择显然是独得黄金。

三个参与人时，两人时的结论变成了已知条件。 3号需要一票就能超过半数，他知道无论如何，2号都会为了独得100块金子而反对，讨好2号没有意义。但1号只要得到微弱的好处就会支持3号。所以分配方案是99：0：1。

依此类推，4号的方案是：99：0：1：0。5号的是：98：0：1：0：1。而这之后发展到无穷参与人的结论都是在此基础上推导的。

其他对海盗博弈的引用或研究则常见于趣味数学题中。[3]篇幅所限，我们不多做论述。 然而，笔者见到这个博弈问题后，感觉原始投票比例的设定不符合现实社会规则，并尝试改进（事实证明，投票比例变动与结果息息相关）。我们现在看一种经典的投票比例：三分之二多数。

现在题目变成了“只有达到三分之二多数的海盗支持的方案才能通过，并且在同等效力的方案中，提议者会优先讨好实力强的海盗（这样会简化计算）。”同时需要改变的另一题设是：“海盗们将按实力顺序排序，由最弱的海盗先提出分配方案，并依此类推。”因为只剩两名海盗時，2号提出任何方案时，1号都不会同意，这样1号可以把2号扔出船外，自己独得100块金子。我们只有让方案的顺序发生变化来实现弱肉强食的自然法则！

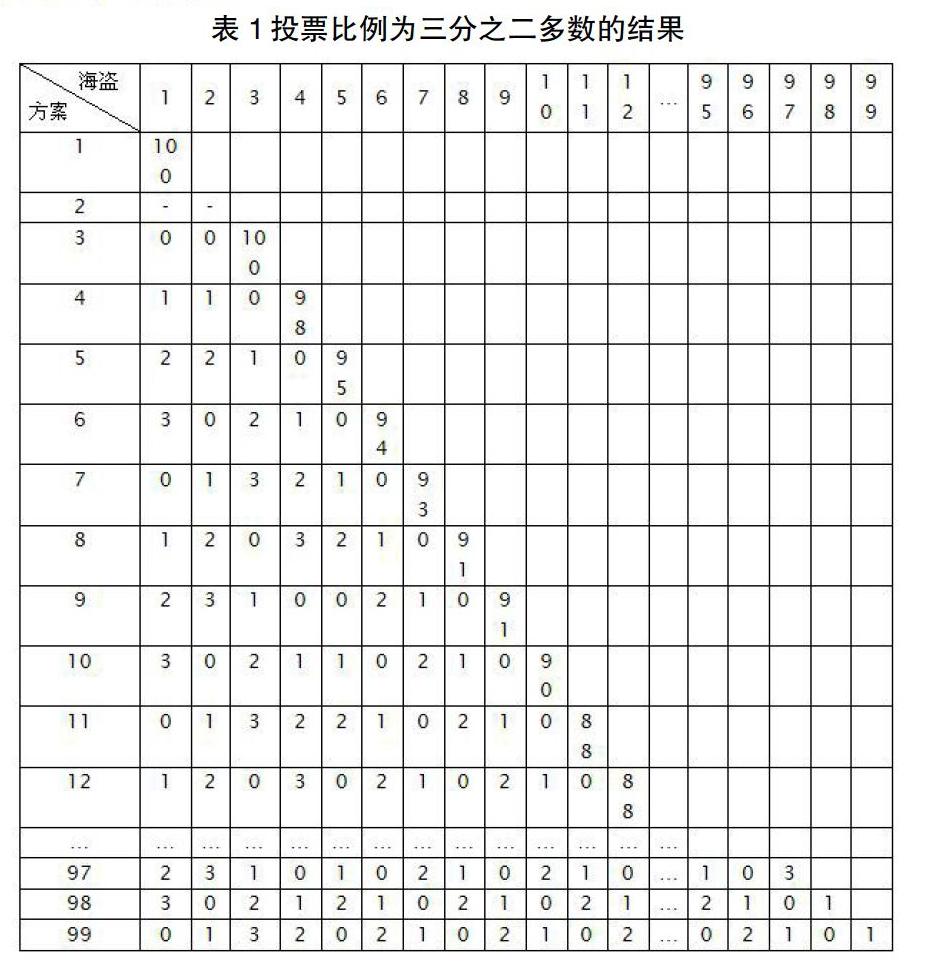
接下来3号依然会独吞黄金。具备基本的分析思路以后，类推时我们采用表格法：

推导进行到12号时，我们发现了规律：从6号的方案开始，实力位居前四的海盗们将稳得6块金子。其中编号能被4整除的方案，按顺序表示为：1：2：0：3。编号被4除余1的方案，按顺序表示为：2：3：1：0。编号被4除余2的方案，按顺序表示为：3：0：2：1。编号被4除余3的方案，按顺序表示为：0：1：3：2。编号大于6的方案从5号之后则进入另一规律，制定方案的海盗会按0：1：2的顺序，循环往复的给比自己编号靠前的海盗逆序分配金子，直至分配到5号。剩余的金块则留给自己。

99号是最后一个能自己留下一块金子的海盗。他总共得到66票支持，刚好达到三分之二。100号虽然一无所有，但他买通了66名海盗，加自己共67票刚好保住一命。101号就没那么好的运气了，但他用实际行动挽救了102号。

由于题设原因，不能被3整除的解远比能被3整除的解苛刻，得出的能被3整除的解要比不能被3整除的解小，考虑到实际意义，我们将舍掉所有不能被3整除的解。整理一下得到结论，99号之后的幸存者编号为N=99+3n（n=0，1，2，…）

现在我们看到，只要将投票比例稍作改变，我们结果与史都华教授的结论就刚好相反了：是强者获得了财富而不是弱者。在学习和工作中，我们总能看到前人总结的很多“真理”。但真理与谬误之间往往只差了一点，只要开阔思路，不断创新，我们就可能颠覆权威。这同时也提醒我们，自己在得出结论时，也应反复论证模型的合理性，尽量多角度的考虑问题。