小电流接地系统单相接地故障测距方法探讨

张月光

国网上海奉贤供电公司

小电流接地系统单相接地故障测距方法探讨

张月光

国网上海奉贤供电公司

以小电流接地系统中的中性点不接地系统为例，进行单相接地故障分析，在Matlab/Simulink平台上搭建中性点不接地系统模型，针对中性点不接地系统单相接地故障测距问题，引入回归型支持向量机理论进行有意义的尝试，并给出了测距仿真分析结果，结果表明该方法具有一定的可行性。

小电流接地系统；故障测距；回归型支持向量机；单相接地

在我国，6 kV以上、110 kV以下的配电网多采用小电流接地方式。在电力系统常见的故障中，单相接地故障的发生率最高且占有相当大的比例。单相接地故障发生时，由于非故障相对地电压升高（完全接地时升至线电压值），系统中的绝缘薄弱点可能击穿，造成短路故障。故障点所产生的电弧，会烧坏设备并可能发展成相间短路故障［1］。因此，当小电流接地系统发生单相接地故障时，尽快选出故障线路，找出故障点，对配电网的稳定运行有着重要的现实意义。但是，小电流接地系统故障选线与测距技术是多年来一直未能很好解决的一个难题［2］，针对小电流接地系统单相接地故障测距问题，引入回归型支持向量机理论和损失函数概念，在Matlab/Simulink平台下搭建小电流接地线系统模型，运用支持向量机原理对该系统进行了单相接地故障测距的研究，并进行仿真分析，验证该方法的正确性和可行性。

1　小电流接地系统故障分析及仿真模型搭建

1.1小电流接地系统单相接地故障分析

以正常运行的单条线路为例，当系统某一相发生单相接地故障（如A相）时，如图1（a）所示，由于接地故障相相对地的电压降低为零，故障点处会出现明显的不对称，主要表现为：

（1）故障相对地电压为零，非故障相对地电压升高为线电压

（2）中性点对地电压大小升高为相电压值（方向与故障相电压相反）

（3）系统中出现零序电压，其大小等于系统正常运行时的相电压

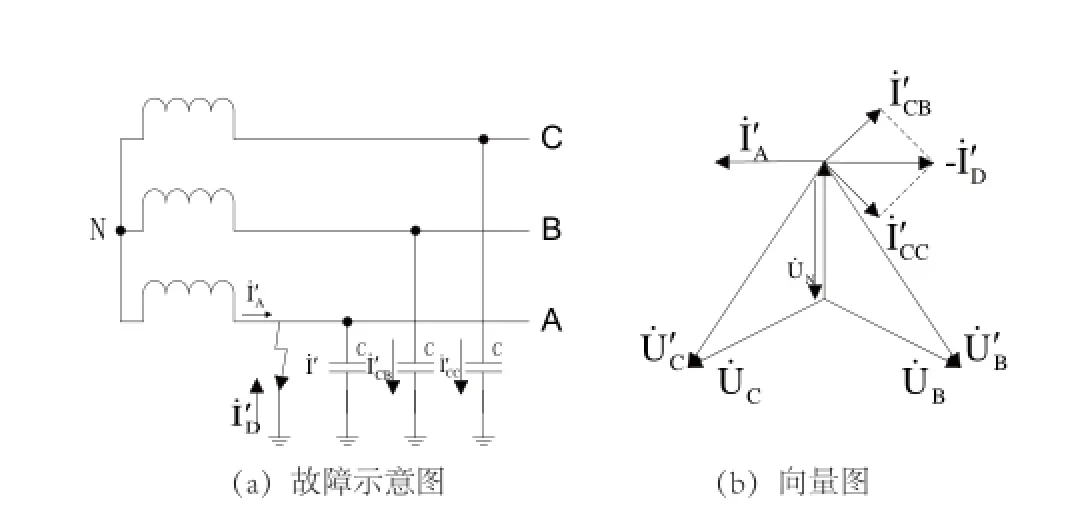
图1　中性点不接地系统的单相接地故障示意图和相量图

（4）接地故障点处的电流大小等于全部线路对地电容电流的总和，其相位超前于零序电压90°

中性点不接地系统发生单相接地故障时的示意图和相量图如图1所示。由上述分析可知，当系统发生单相接地时，系统中各点电压如式（1）所示。

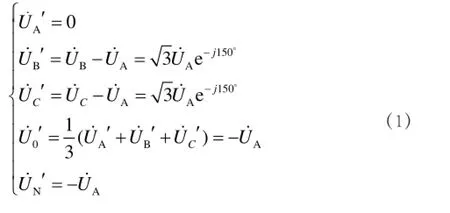
同理可知，系统中各点电流如式2所示：

由此可见，对于单条线路而言，当线路发生单相接地故障时，故障线路始端零序电流为零。同理可知，对于运行中的多条线路，当系统发生单相接地故障时，非故障线路的零序电流为其本身的电容电流，电容性无功功率的方向为由母线指向线路，故障线路的零序电流则等于所有非故障线路零序电流的向量和，其电容性无功功率的方向为线路流向母线，与非故障线路上的相反。

1.2小电流接地系统仿真模型搭建

针对中性点不接地系统，使用Matlab/Simulink仿真平台搭建其仿真模型，通过仿真结果更直观地观测系统的稳态、暂态特性。在仿真模型中，电源连接方式采用Y形接线，输出电压取10.5 kV。输电线路3条，线路长度分别为10 km、20 km、15 km，线路负荷分别为1 MW、0.2MV、2 MV。设置系统中第3条出线A相在0.04 s时发生单相接地故障，故障线路的三相电压波形如图2所示。

由图2可知，系统在0.04s A相发生单相接地故障后，A相对地电压变为零，B相C相相对地电压升高倍，但线电压仍然保持对称，从而验证了中性点不接地系统单相接地故障电压分析理论的正确性。

2　回归型支持向量机理论

支持向量机（Support Vector Machine，SVM）是一种比较好的实现了统计学习理论VC维和结构风险最小化思想的方法，其重点思想在于最优超平面的构造及非线性问题的处理。支持向量机最初是用来解决非线性分类的问题，为了能把其推广到回归估计中去，通过引入一个损失函数（ 不敏感损失函数）来实现，从而得到了支持向量回归算法（Support Vector Regression，SVR）［3］。

给定训练集：

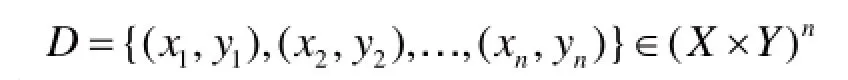
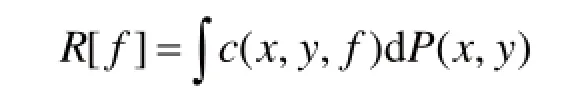
达到最小。这里，我们只知道训练集D，而概率分布P（x，y）是未知的。

在分类算法中，只有间隔区域内的点才对决策函数提供信息，解的稀疏性对在高维空间中处理大量数据非常重要。这里引入一种新型损失函数，即ε不敏感损失函数［4］，它不仅使回归型支持向量机具有鲁棒性，同时也具有稀疏性。

ε不敏感损失函数的形式为

ε不敏感损失函数的含义是，如果在x点的预测值f （x，a）和实际值y的差值不超过ε，就认为预测值f （x，a）是无损失的，尽管此时这两个值并不一定完全相等。所以，在ε区域之内的点对损失函数没起到作用，这是其他类型的损失函数所不具备的，因此 不敏感损失函数有着较好的稀疏性［5］。

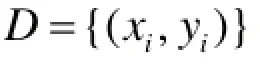
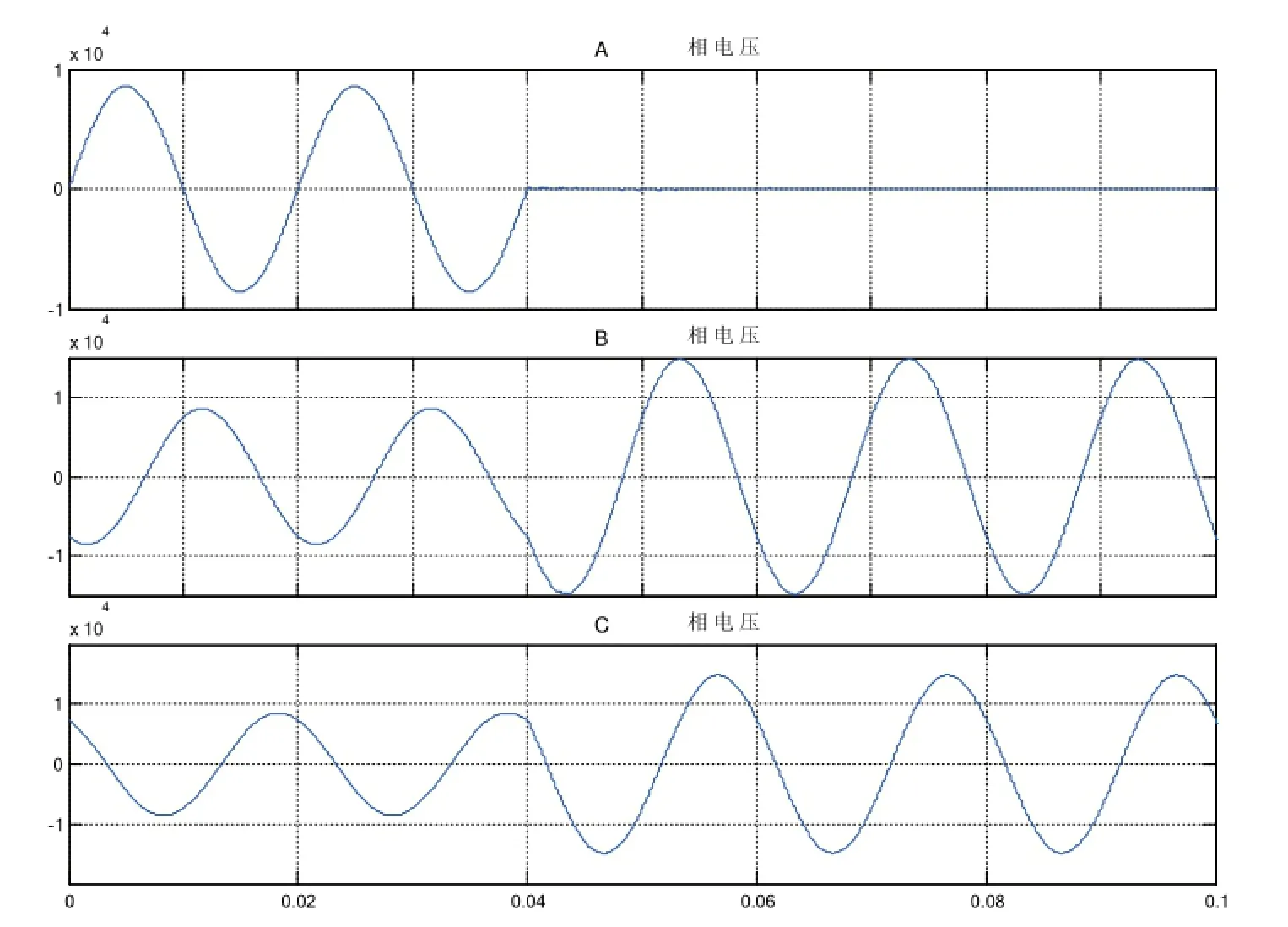
图2　故障线路三相电压波形

采用线性ε不敏感损失函数，假设所有训练数据在精度ε下无误差地用线性函数拟合，即

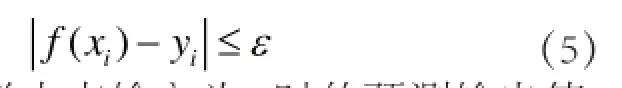
其中，f（xi）是在样本点输入为xi时的预测输出值，yi为真实输出值。

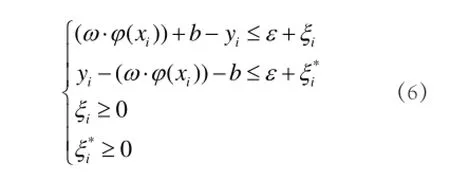
优化目标函数为

构造拉格朗日函数来求解上述的凸二次规划问题，即

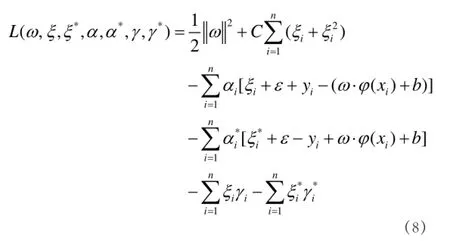
将式（9）代入式（8），有

因此，式（7）的凸二次规划问题可以转化为下面的对偶二次规划问题求解。

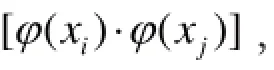
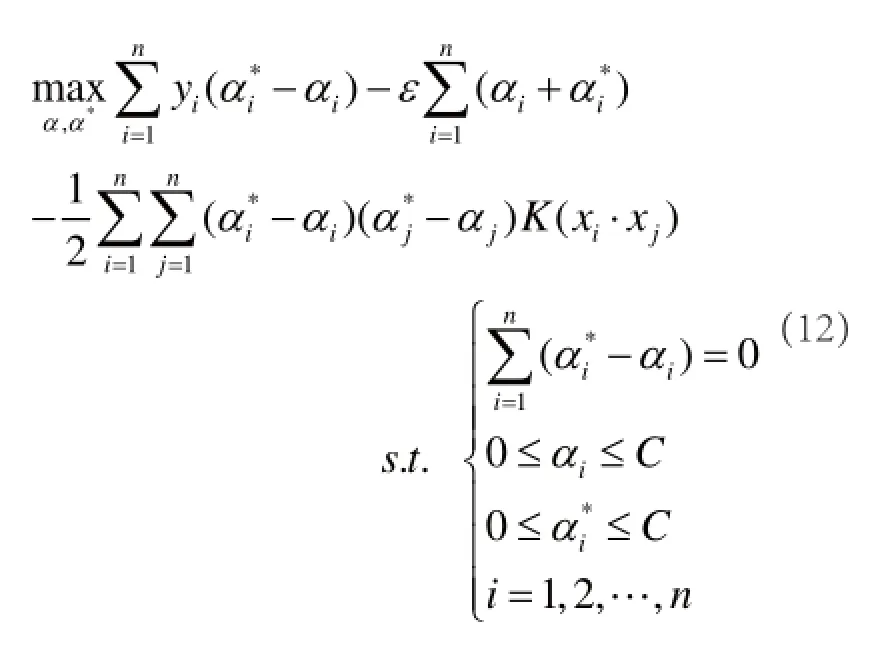
将式（9）代入式（4）得到的非线性SVR的回归函数为

综上所述，非线性SVR的基本思想是通过核特征空间的非线性映射算法把样本点变换到一个高维Hilbert空间中的训练点，然后再在这个空间中对映射后的训练集进行线性回归［6］。

通过上述分析可知，采用支持向量机解决回归函数估计问题，必须首先确定3个自由参数：不敏感度、规则化参数和核函数参数，然后再采用支持向量机进行回归估计［7］。

3　支持向量机回归仿真及测距结果

3.1训练样本和测试样本的选取

以长度为10 km的线路1发生单相接地故障为例，在接地电阻分别取0.01Ω，1Ω和100Ω， 故障初始相角分别取0°，60°和90°时，进行故障距离步长为1km的生成样本，共计3×3×10=90组样本。

在样本中通过自变量来找到其所对应的因变量，即分类问题中的标签，在回归问题中被称作因变量或目标变量。如在10%处的自变量对应的因变量设为1，在20%处的自变量对应的因变量设为2，依此类推，共计10个。随机抽取其中的80组作为训练样本，其余10组作为测试样本。线路2和线路3故障时，也是这样处理。这里给出部分训练样本的数据，如表1所示。

仿真选择Gauss径向基核函数即RBF径向基核函数，其中分别选择c参数为128，最g参数为0.003 906 3，CVmse为0.642 16。

3.2样本训练

将训练样本数据、训练样本标签、训练参数，通过libsvm工具箱进行支持向量机样本的训练，使用以下句柄格式：

model=svmtrain（train_labels，train_data，option）；

其中，model为所得的训练模型，svmtrain为支持向量机训练函数，train_labels为训练样本标签，train为训练样本数据，option为训练样本时所选定的参数。

训练样本的拟合效果，如图3所示。

图3中，蓝色圆圈表示实际值，红色三角表示拟合值。经过计算，训练样本的均方误差为0.43113，平方相关系数为0.95359，其中平方相关系数越接近于1越好。

3.3测距结果

在simulink平台下，将训练模型、测试样本目标变量和测试样本数据输入测试样本进行支持向量机的测距测试。使用以下句柄：

［predict，mse］= svmpredict（test，test_ data，model）；

其中，predict为支持向量机回归轨迹测距的结果，svmpredict为拟合预测函数，test为测试样本目标变量，test_data为测试样本自变量数据，model为上一步得到的训练模型。下面给出支持向量机回归估计的测距结果，如图4所示。

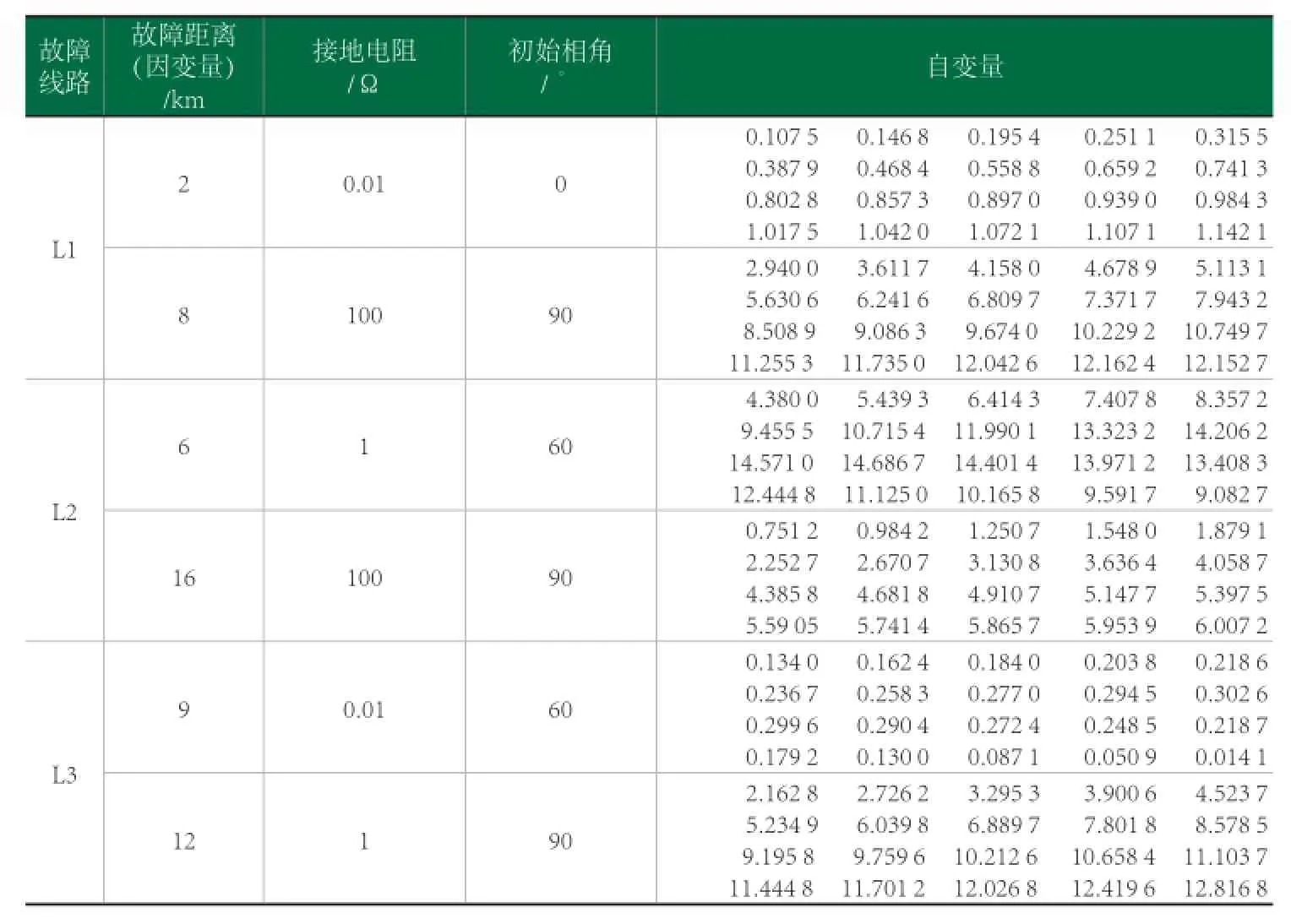
表1　部分测距训练样本

图3　训练样本的拟合效果

图4　支持向量机回归故障测距结果

从图4可以看出，测距的效果良好。经过计算，测试样本的均方误差为0.048476，平方相关系数为0.99417。可见，使用支持向量机作为故障测距的工具也有一定的可行性。在matlab/simulink平台上搭建中性点不接地系统模型，针对中性点不接地系统单相接地故障测距问题，引入回归型支持向量机理论进行有意义的尝试，并给出了测距仿真分析结果，结果表明该方法具有一定的可行性。

4　结 语

本文以小电流接地系统中的中性点不接地系统为例，进行单相接地故障分析，回归型支持向量机（SVR）的工作原理，并将其应用到中性点不接地系统单相接地故障测距中。对故障测距的样本进行提取，进行回归型支持向量机的训练，给出了训练样本的拟合效果，最后对测试样本进行拟合，给出了测距的结果，从结果中看，整体的拟合效果良好，说明回归型支持向量机在智能故障测距中的应用中具有一定的可行性和参考价值。

［1］ 要焕年，城市电网中性点接地方式［J］.电网技术，1991，15（3）：15-18.

［2］ 李润先.中压电网系统接地实用技术［M］.北京：中国电力出版社，2000.

［3］ 胡良谋，曹克强，徐浩军，等.支持向量机故障诊断及控制技术［M］.北京：国防工业出版社，2011.

［4］ 杨俊燕，张优云，朱永生.ε不敏感损失函数支持向量机分类性能研究［J］.西安交通大学学报，2007，41（11）：1315-1320.

［5］ 陈勇，徐建敏.ε-不敏感的光滑支持向量回归机的收敛性［J］.计算机工程，2010，36（15）：185-190.

［6］ 杨金芳.支持向量回归在预测控制中的应用研究［D］.华北电力大学，2007.

［7］ 何学文.基于支持向量机的故障智能诊断理论与方法研究［D］.中南大学，2004.

Low Current Grounding System Single Phase Grounding Fault Distance Measurement Method

Zhang Yueguang
State Grid Shanghai Fengxian Power Supply Company

The article takes neutral ungrounded system among low current grounding system as example and analyzes single phase grounding fault. It sets up neutral ungrounded system model at Matlab/Simulink platform to focus on neutral ungrounded system single phase grounding fault distance measurement problem. It applies regression type support vector machine theory as meaningful trial and provides distance measurement simulation analysis results， which shows that this method is feasible.

Low Current Grounding System， Fault Distance Measurement， Regression Type Support Vector Machine， Single Phase Grounding

10.13770/j.cnki.issn2095-705x.2016.08.005

张月光：（1987-），男，硕士，从事电网调度工作。