问题驱动教学在线性代数教学中的应用

王剑

（天津职业技术师范大学理学院，天津300222）

问题驱动教学在线性代数教学中的应用

王剑

（天津职业技术师范大学理学院，天津300222）

以线性代数教学中的实施过程为载体，针对传统数学教学中出现的理论与实际联系不够紧密的问题，探讨了问题驱动原则的教学问题设计、知识架构以及数学建模思想。

问题驱动；数学建模；探究式教学

问题驱动教学是激发学生学习主动性和积极性，培养加强学生实践能力和综合素质的应用性教学模式。问题驱动原则是在教师的启发引导下，结合教学内容和实际问题，不断发现问题、提出问题、分析问题及解决问题的过程。美国教育家布鲁巴克认为：“最精湛的教学艺术，遵循的最高准则，就是学生自己提出问题”。高校线性代数教育的一个重要目的是培养学生的创新意识与应用能力，主要贯穿在“理解理论知识—理论联系实际—解决实际问题”3个层面［1］。问题是数学发展的原始驱动力，也是增强数学趣味性及提升教学效果有效性的源泉。本文以问题驱动教学模式下的线性代数课程设计为例，结合学生实际情况，探讨问题驱动教学的实践和效果。

1　问题驱动教学模式知识框架的构建

传统数学教学模式中，学生在学习过程中基本是被动接受知识，缺少主动思考和参与，这不仅不能深刻理解知识的内涵，同时也削弱了自身的学习兴趣。对于高职院校学生来说，如何将所学知识更好地应用到实际中是核心理念［2］。如果能有效结合实际问题，通过自主学习形成对数学知识的接受和应用，那么学生的学习积极性及创新能力都会有较大提高［3］。因此，问题驱动教学模式的关键是根据课程内容合理设置实际问题，在学生的新旧知识互动过程中搭建知识桥梁。

1.1利用本源问题引入数学原理

在讲解线性代数矩阵运算知识点之前，尝试先让学生思考如下实际问题，通过分析和解决问题体会数学知识的运用，逐步在典型实例对比中提取问题的共性，归纳和总结新的数学概念和方法。

例1某班学期末甲、乙、丙三人高等数学总评成绩的测算。

分析按照教学考核标准，学校每学期学生高等数学成绩分为3部分，其中平时、期中与期末分别占20%、30%和50%，3部分成绩的总和为学期末总成绩，即

平时期中期末

806070甲0.2平时

708086乙0.3期中

908094丙0.5期末则甲、乙、丙3人总成绩分别为：

80×0.2+60×0.3+70×0.5=69

70×0.2+80×0.3+86×0.5=81

90×0.2+80×0.3+94×0.5=89

记上述数表为矩阵形式，得到

为使学生体会矩阵乘法运算的本质特征，思考解题过程中蕴含的矩阵运算知识，下面从多方面给出关联矩阵运算的实例。

例2某家电公司向3个商店发送4种产品的数量如表1所示，4种产品的售价及重量如表2所示。问：该公司向每个商店出售产品的总售价及总重量分别是多少？

表1　某家电公司向3个商店发送4种产品的数量台

表2　4种产品的售价及数量

分析：记录4种产品数量矩阵为A，售价和重量矩阵为B，则

例3某个城镇中，每年有30%的已婚女性离婚，20%的单身女性结婚，城镇中有8 000位已婚女性和2 000位单身女性。假设所有女性的总数为一常数，1年后有多少已婚女性和单身女性？

分析：可按照如下原则构造矩阵A（第1行元素分别为1年后仍处于婚姻状态的已婚女性和结婚的单身女性的百分比，第2行元素分别为1年后离婚的已婚女性和未婚的单身女性的百分比）。因此

1年后已婚女性和单身女性人数可表示为：

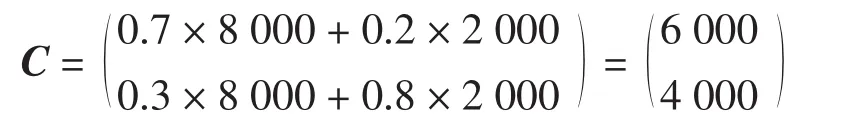
结论：1年后将有6 000位已婚女性和4 000位单身女性。

通过上述例题，让学生结合实例体会矩阵的乘法运算。这里着重强调数学教学不局限于知识点本身，而是将数学与学生生活实际联系起来，让学生能够在案例分析的基础上把数学知识的基本原理和基本方法掌握好，从而逐步提高运用理论知识分析实际问题的能力。

1.2多角度探究数学原理，构建知识框架

在数学知识传授过程中，要重视引导学生多个角度探究问题的数学原理。从教学基本内容出发，总结典型问题和实例，让学生通过练习和思考归纳出相关数学知识的基本性质和常用方法［4］。当然，相关问题的选取不仅要与教学内容和教学目标相吻合，而且要具有一定的导向性，使学生经过自主探究，形成新的认知，体验发现的乐趣。

前面例1中初步应用了3×3阶与3×1阶矩阵乘法运算知识，为进一步让学生深刻体会矩阵的乘法运算原理，下面给出包含矩阵可乘原则、乘积阶数及乘积元素3个要素的相关例子。

注意：例6结论AC=BC，但A≠B。即一般来说，由AC=BC，且C≠0不能推出A=B。

2　结合数学建模思想的创新思维培养

教师教学是一种有目的、有计划的创造性活动，学生学习知识最看重的就是知识的应用，学以致用本身也是所有学科的价值所在。切实让学生体会数学与现实生活之间的联系，是培养学生数学素养和应用能力的一个重要教学目标［5］。简而言之，用数学语言抽象概括实际问题，从数学角度来刻画或近似地反映实际问题，得到关于实际问题的数学描述，恰是数学建模的思想［6］。下面结合稍复杂的应用题，介绍数学建模的思想和解题过程，让学生体会用数学知识解决实际问题的方法和步骤［7］。

例7常染色体遗传的规律问题：动植物都会将本身的特征遗传给后代，后代从每个亲体的基因对中各继承一个基因，形成自己的基因对，即基因型，基因对就确定了后代所表现的特征。试考察第n代基因型分布在初始条件下的表现形式。

（1）问题分析

a.模型准备

如果考虑的遗传特征是由2个基因A、a控制，那就有3种基因对，记为AA、Aa和aa。这里AA、Aa表示同一外部特征，认为基因A支配基因a，即基因a对A来说是隐性的。

双亲体结合形成后代的基因型概率矩阵为：

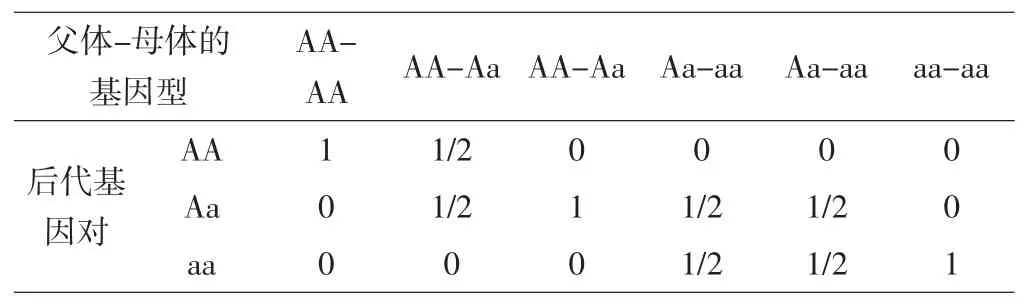
父体-母体的基因型AAAAAA-AaAA-AaAa-aaAa-aaaa-aa后代基因对AA11/20000 Aa01/211/21/20 aa0001/21/21

b.模型假设

设an、bn、cn（n≥2）分别表示第n代基因型为AA、Aa、aa的样本占总数的百分比，且an+bn+cn=1。记第

c.模型建立

为简化问题，设定初始条件。控制结合：显性患者aa不能生育后代，正常人AA与隐性患Aa都必须与正常人AA结合生育后代，则aa所占的比例Cn=0，设第n代基因型分布为：

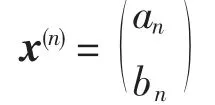
初始条件下，双亲体结合形成后代的基因型概率矩阵为：

父体-母体的基因型AA-AAAA-Aa后代基因对AA11/2 Aa01/2

引导学生逆向思维，逐步建立双亲体结合形成后代的基因型数学模型为：

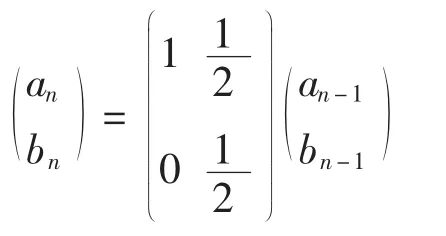
其中an+bn=1。

第n代基因型分布与第1代基因型分布之间的关系为：

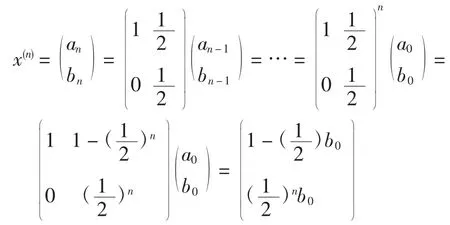
d.模型分析

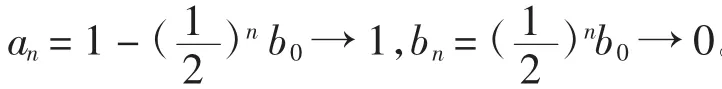
（2）结果分析

通过构建数学模型，可用第1代基因型表示出第n代基因型分布，再结合极限思想，得出当n充分大时，第n代基因型分布趋于一个定值，表明经过足够长的时间，隐性患者消失。

3　提升综合应用能力的教学问题设计

数学教学的深化和发展是通过进行发现问题并解决问题的大量训练来完成的。数学学习往往要历经“发现问题—分析问题--解决问题”，然后转变为“数学理念”的认知过程［8］。问题驱动教学不仅可以培养学生利用数学知识解决实际问题的综合能力，而且有利于培养学生数学思维的灵活性［9］。教学中要善于设计一系列具有针对性、层次性和挑战性的开放式问题，具有多种实际背景和多种解题方案，以问题为目标，激励和引导学生辩证思考，促使学生在理解和掌握数学知识的同时，能将其与其他学科相结合，实现知识的综合应用。

4　结束语

学生通过多层次多角度理论联系实际的实践训练，有利于深刻理解矩阵乘法的量化定义，提升数学应用意识。实践证明，在线性代数教学中坚持问题驱动教学原则，有助于培养学生的主体意识和主动精神，提高学生的创新思维能力，使他们不局限于数学基本理论的思考，而是广泛联系社会实际，逐步提高自己的实践能力和创新能力，从而达到从数学学习到个人综合素质的提升和发展。

［1］杨宪立，赵自强.问题驱动原则在高等数学教学中的运用［J］.河南教育学院学报，2014，23（1）：49-52.

［2］郑君文，张恩华.数学学习论［M］.南宁：广西教育出版社，1996.

［3］袁勇.问题驱动式教学模式在理工类高等数学中的应用探索［J］.教育与教学研究，2015，29（9）：82-85.

［4］李以渝.高等数学探究式教学案例设计及类型分析［J］.四川工程职业技术学院学报，2013，24（1）：76-77.

［5］徐志科.数学建模：高职数学教改的突破口［J］.职业教育研究，2007（8）：100-101.

［6］郭景石.高职数学教育改革中的数学建模［J］.教育与职业，2011（26）：97-98.

［7］姜启源.数学模型［M］.北京：高等教育出版社，2011.

［8］孙咏梅.谈高职数学教学中学生创新能力的培养［J］.教书育人：高教论坛，2014（4）：20-21.

［9］张艳霞.对话理论视角下高职数学教学创新探究［J］.教育与职业，2015（13）：101-103.

Application of problem driven teaching in linear algebra

WANG Jian
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

To deal with Theory Contact Practice in traditional mathematical teaching theory research，which is the carrier of linear algebra curriculum，this paper analyzes the problem driven principle for research-style teaching，knowledge structure and mathematical modeling thought in it.

problem driven principle；mathematical modeling thought；research-style teaching

G712；O151.2

A

2095－0926（2016）02－0053－04

2016-01-19

天津市教育科学“十二五”规划课题（VE2016）.

王剑（1980—），男，讲师，博士，研究方向为非交换几何.