一种多信号时差估计的子空间方法

丁学科，周志平，胡泽鹏，汤四龙，万　群

(1.同方电子科技有限公司，江西 九江　332007； 2.电子科技大学 电子工程学院，成都　611731)



【信息科学与控制工程】

一种多信号时差估计的子空间方法

丁学科1，周志平1，胡泽鹏2，汤四龙1，万群2

(1.同方电子科技有限公司，江西 九江332007； 2.电子科技大学 电子工程学院，成都611731)

针对在同一时段、同一频带上多目标发射信号的情况下常用的测定信号到达时差的时域测定方法和频域测定方法性能恶化甚至失效的问题，提出了一种测定多个时频混叠信号到达时差的方法；利用3个或3个以上的无线电接收机接收信号、测定时频混叠的多个信号到达各接收机之间的时差，可在一定程度上满足抗干扰、多目标同时无线电定位的应用需求。仿真实验结果表明，提出的子空间时差估计方法可较准确的估计多信号时差。

多信号；时差估计；子空间

1　概述

在通信、雷达、声纳、遥测等领域，利用两个无线电接收机接收同一个辐射源发射的信号，以测定该辐射源发射的信号到达这两部无线电接收机的时间之差(简称信号到达时差或时延)，是对发射信号的辐射源进行无线电定位的关键技术之一，有着广泛而重要的应用价值[1-2]。

常用的测定信号到达时差的时域测定方法[3-4]和频域测定方法[5-6]都是假设一个无线接收机接收的信号与另一个接收机接收的信号之间存在一定的时差关系，可通过时域采样序列的时间对齐或频域序列的线性相位对齐测定同一目标发射信号到达这两部接收机的时差。在实际应用中，由于信号的转发、中继、空间复用以及存在干扰信号的场合等原因，经常发生在同一时间段内、同一段频谱上多目标发射信号的情况，由于各目标发射的信号到达两个接收机之间时差一般是不同的，使得一个接收机接收的信号经过一定的时差平移后与另一个接收机接收到的信号的形状不一致，导致常用的测定信号到达时差的时域测定方法和频域测定方法性能恶化，甚至失效[7-8]。

为此，本文提出了一种测定多个时频混叠信号到达时差的方法，该方法利用3个或3个以上的无线电接收机接收信号、测定时频混叠的多个信号到达各接收机之间的时差，可在一定程度上满足抗干扰、多目标同时无线电定位的应用需求。

2　多信号时差估计模型

假设K是接收机的个数，各接收机接收信号的频域序列为

(1)

其中k为接收机的序号，k=1,2,…,K，yk(j,t)表示在第t个采样时刻第k个接收机接收信号的时域采样序列的快速离散傅里叶变换的第j个值(即:第k个接收机接收信号在第t个采样时刻的频域序列的第j个值)，t=1,2,…,P，P为采样时刻的个数，j=1,2,…,J,J是快速离散傅里叶变换的长度，xk(m,t)是第k个接收机接收信号在第t个采样时刻的时域采样序列的第m个采样值，m=1,2,…,M，M是接收机接收信号的时域采样序列的长度。

可直接将第t个采样时刻所有接收机接收信号的频域序列写成向量的形式：

(2)

其中

(3)

是在第t个采样时刻第k个接收机接收信号的频域序列对应的向量。

所有接收机接收信号的样本自相关矩阵为

(4)

其中yH(t)表示向量y(t)的共轭转置。

对样本自相关矩阵进行奇异值分解：

(5)

下面先介绍时频重叠的多信号时差估计方法，再利用仿真实验验证其有效性，最后给出结论。

3　多信号时差估计算法

当一个辐射源发射信号时，式(2)可写成：

其中IJ表示J阶单位矩阵，αk1和τk1分别表示第k个接收机接收的目标信号的幅度和时差(不是一般性，假设第1个接收机为参考接收机，即α11=1，τ11=0)，s1(t)表示目标信号的J阶频域向量，vk表示第k个接收机的J阶频域噪声向量，Φ(τk1)是J阶对角矩阵，由下式表示：

fΔ表示频率间隔，diag( )表示以向量元素为对角元素的对角矩阵，t=1,2,…,P，k=1,2,…,K。

当位于不同位置的N个辐射源发射信号时，则对应式(2)，有：

(6)

其中

αkn和τkn分别表示第k个接收机接收的第n个目标信号的幅度和时差(同理，α1n=1，τ1n=0)，sn(t)表示第n个目标信号的J阶频域向量，Φ(τkn)是J阶对角矩阵，由下式表示：

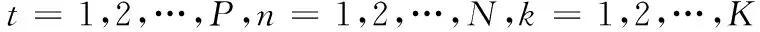
因此，由式(5)可得噪声子空间矩阵U为

(7)

式(7)中wNJ+1,wNJ+2,…,wKJ为样本自相关矩阵R的奇异向量。

定义时差矩阵为：

(8)

其中G(β2,β3,…,βK)为时差矩阵，βk分别表示第k个接收机接收的信号相对于参考的第1号接收机接收的信号时差值：

分别表示第k个接收机接收信号相对于参考接收机(即第1号接收机)接收信号的时差对齐矩阵，i表示满足i2=-1的纯虚数，T是时域采样周期，J是快速离散傅里叶变换的长度，k=2,3,…,K。

由噪声子空间矩阵确定时差谱：

(9)

其中‖ ‖表示向量范数，βk=qkα，qk=-Q,-Q+1,…,Q-1,Q，qk为搜索的时差值的序号，k=2,3,…,K，α为搜索的时差间隔，搜索的时差个数为2Q+1，UH为噪声子空间矩阵U的共轭转置矩阵。

搜索时差谱的峰值，由峰值所在的位置即可得第k个(k=2,3,…,K)接收机接收的信号中这N个辐射源发射的信号相对于第1个接收机接收的这N个辐射源发射的信号的时差。

4　仿真验证

记M是接收机接收信号的频域序列的长度，则k个接收机接收N个信号的频域复值测量的实数个数为2kM，未知实数的个数为N个信号的2NM个频域值加上N(k-1)个时差值，因此，多信号时差估计问题可解的必要条件是

2KM>2NM+N(k-1)

由于一般有M≥1，因此，当信号个数为2时，至少需要3个接收机。

假设接收信号的有3个接收机，其序号分别为1、2、3，并默认序号为1为参考接收机。辐射源为2个时频重叠的、码速率为40 kbps、基带频率为100 kHz的BPSK信号，信噪比都是20 dB。相对于第1个接收机接收的信号，第2、3个接收机接收的信号中的第1个目标发射的信号到达时差分别为-973 ns和17 106 ns，第2个目标发射的信号到达时差分别为-7 270 ns和-2 042 ns。接收机时域采样频率应大于基带频率，此处设置为200 kHz(对应采样周期为5 μs)，共采样216个值。

仿真实验的目的就是利用这3个接收机接收这2个辐射源发射的时频重叠信号，实现准确测定第2、3个接收机接收的信号中这2个辐射源发射的信号相对于第1个接收机接收的这2个辐射源发射的信号的到达时差的目的。

图1～图3分别给出了第1～3号接收机接收的信号幅度谱，可见，由于在同一时间段内、同一段频谱上不只一个目标发射信号，而各目标发射的信号到达两个接收机之间的时差不同，使得一个接收机接收的信号经过一定的时差平移后与另一个接收机接收的信号的形状不一致，导致常用的测定信号到达时差的时域测定方法和频域测定方法性能恶化，甚至失效。

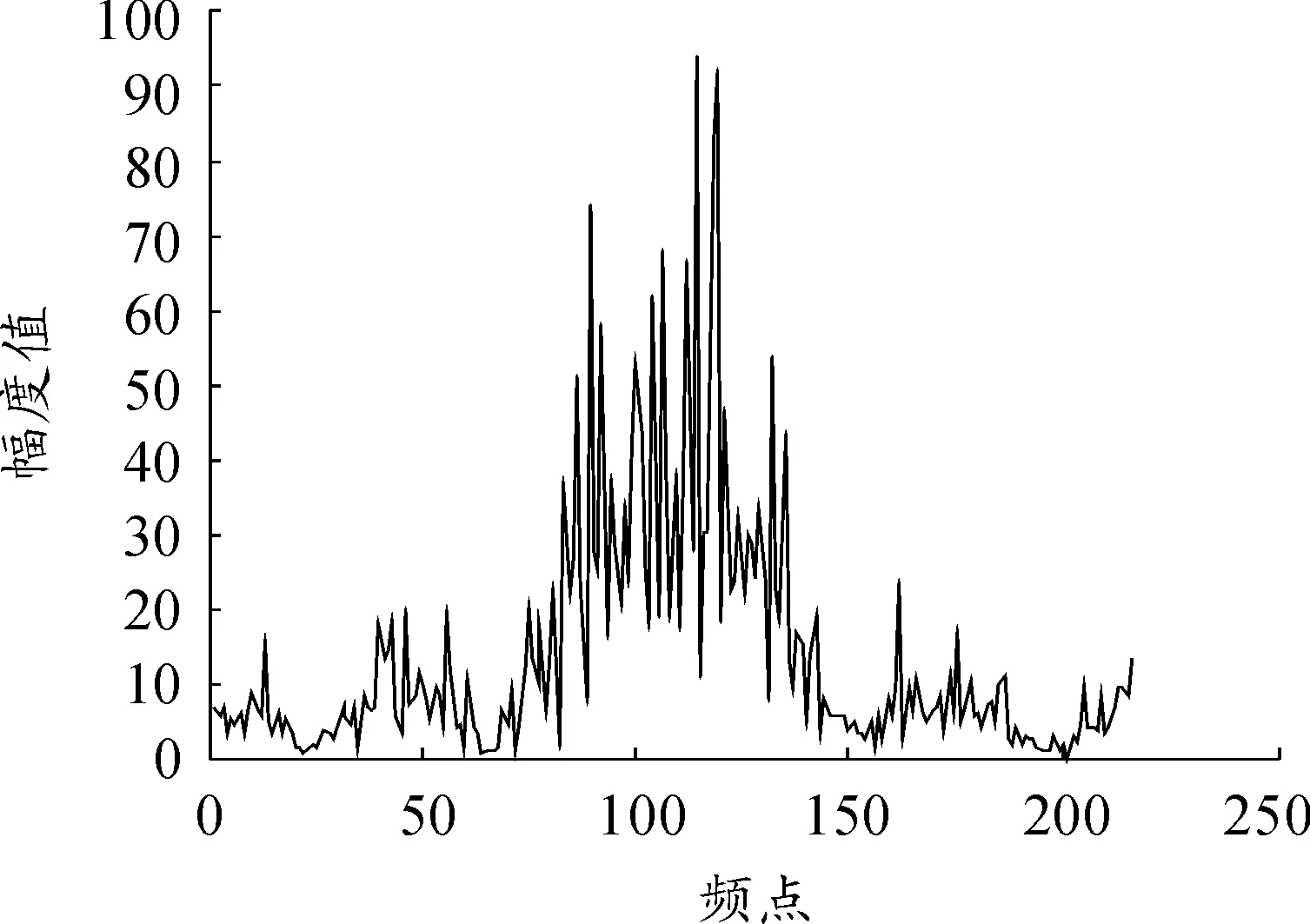
图1　第1号接收机接收信号的幅度谱

图2　第2号接收机接收信号的幅度谱

以测定信号到达时差的时域方法为例，该方法只能测定1个信号的到达时差。图4给出了第2、3号接收机接收的信号与第1号接收机接收的信号的互相关曲线。由互相关的峰值位置可见，相对于第1个接收机接收的信号，测定的第2、3个接收机接收的信号到达时差分别为-4 400 ns和5 800 ns，与这2个辐射源发射的信号到达时差的真实值都不吻合。

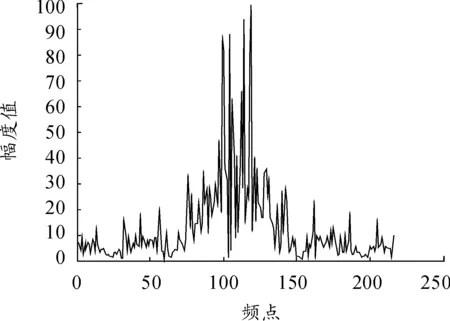
图3　第3号接收机接收信号的幅度谱

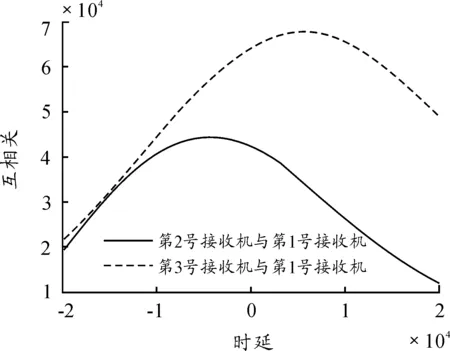
图4　第2、3号接收机接收的信号与第1号接收机接收的信号的互相关曲线

每个接收机只取频点从80～140的61个频点组成频域序列，因此3个接收机接收信号的样本自相关矩阵维数等于183。图5给出的是样本自相关矩阵的奇异值，可见，大奇异值的个数为122(等于信号个数2乘以频点个数61)。因此，可利用第123～183个奇异向量构成噪声子空间。

图6给出本文采用子空间方法得到的时差谱的等高线，由峰值位置测定的第2、3个接收机接收的信号中的第1个目标发射的信号到达时差分别为-1 000 ns(误差27 ns)和17 000 ns(误差106 ns)，第2个目标发射的信号到达时差分别为-7 200 ns(误差70 ns)和-1 800 ns(误差242 ns)。

图5　接收信号样本自相关矩阵的奇异值

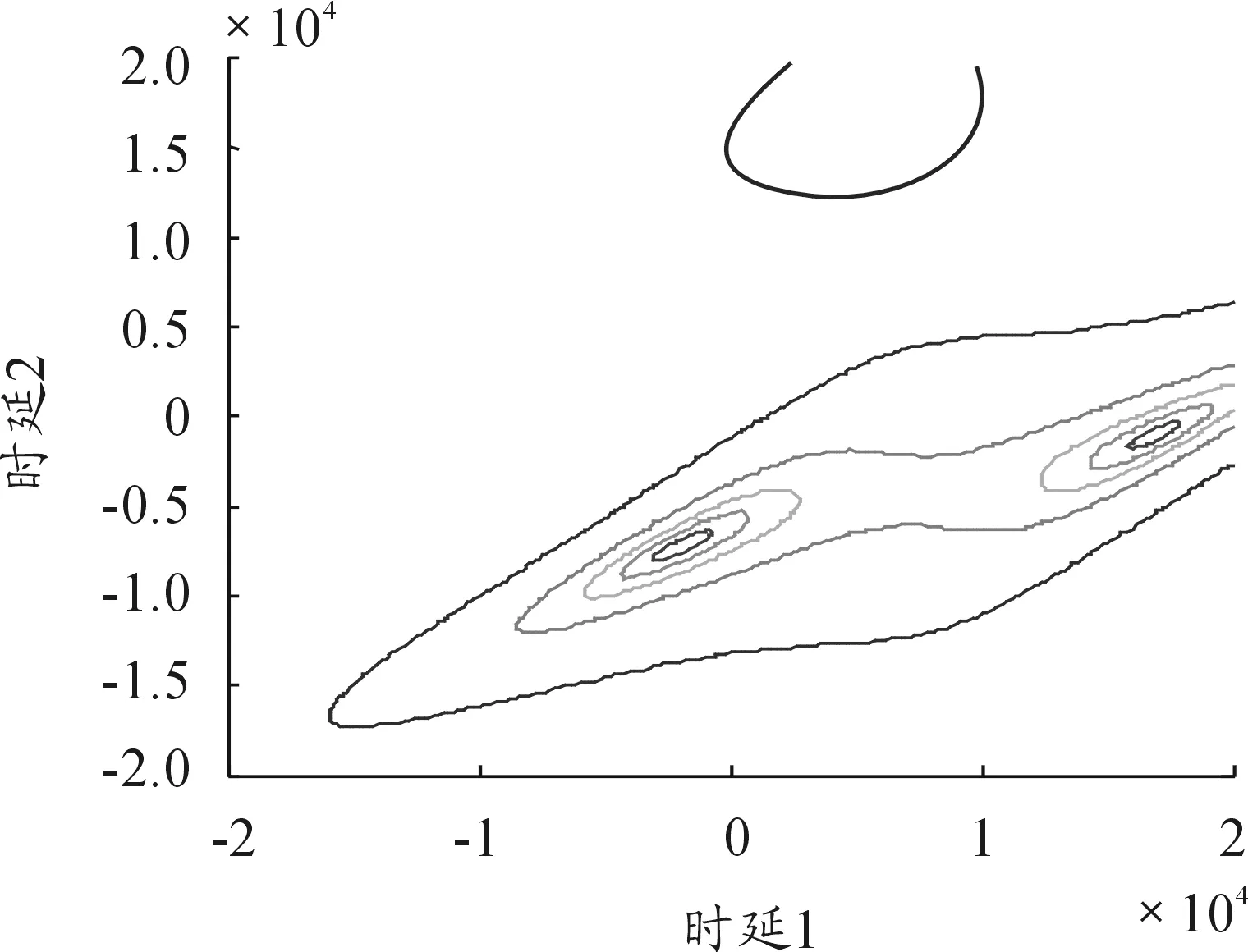
图6　时差谱的等高线

5　结论

时域、频域混叠的多个辐射源发射信号时，使用本文方法可测定多个信号的到达时差，误差小于245 ns，对带宽更宽的信号或增加接收站的个数还可进一步提高时差估计精度。不仅使利用无线电接收机接收信号测定信号到达时差的技术适用于存在时频混叠的干扰信号的场合，还可对不同目标发射的信号的到达时差进行自动配对，为多目标时差定位提供可靠的时差参数估计。

[1]WEN F,WAN Q,LUO L Y.Time-difference-of-arrival Estimation for Noncircular Signals Using Information Theory[J].International Journal of Electronics and Communications,Elsevier,2013,67(3):242-245.

[2]黎英云.微弱多径信号时延估计技术研究[D].武汉:华中科技大学,2009.

[3]钱剑勋.长基线时差定位中定位模糊问题[J].四川兵工学报，2010,31(5):138-140.

[4]王学青，时银水，朱岩.四元平面方阵对空声时延定位误差分析[J].电声技术，2005(11):4-6.

[5]徐保根，万义和，汤四龙，等.不同信道条件下的跳频信号时差估计方法[J].四川兵工学报，2012,33(11):86-88.

[6]徐长根，张飞猛.基于五元阵的炮兵声测数学模型研究[J].国外电子测量技术，2008,27(4):7-9.

[7]刘红宁，李志尊.基于移动机器人的声源定位系统[J].四川兵工学报，2009,30(4):77-79.

[8]何青益，高京晋.短波信号电离层反射时差定位可行性分析[J].电子对抗，2011,141(6):25-27.

(责任编辑杨继森)

A Subspace Method for Time Delay Estimation of Multiple Signals

DING Xue-ke1, ZHOU Zhi-ping1, HU Ze-peng2, TANG Si-long1, WAN Qun2

(1.Tongfang Electronic Science and Technology Co., Ltd., Jiujiang 332007, China;2.School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

Considering on the performance degradation and even failure of either the time domain methods or the frequency domain methods, a subspace based method was proposed to determine the time-difference-of-arrival of multiple signals with the same period of time and band of frequency, by using three or more than there radio receivers to receive the signals. To a certain extent, it meets the needs of the application of anti-interference for target localization and simultaneous radio positioning of multiple emitters. The simulation results show that the proposed method can estimate the time-difference-of-arrival between receivers for multiple signals.

multiple signal; time delay estimation; subspace method

2016-03-22；

2016-04-20

国家自然科学基金(U1533125)

丁学科(1980—)，男，工程师，主要从事阵列信号处理与无源定位研究。

10.11809/scbgxb2016.09.023

format:DING Xue-ke, ZHOU Zhi-ping, HU Ze-peng,et al.A Subspace Method for Time Delay Estimation of Multiple Signals[J].Journal of Ordnance Equipment Engineering,2016(9):96-99.

TN957

A

2096-2304(2016)09-0096-04

本文引用格式：丁学科，周志平，胡泽鹏，等.一种多信号时差估计的子空间方法[J].兵器装备工程学报，2016(9):96-99.