基于Z-number 改进挣值法的工程项目成本进度集成控制分析
2016-10-19赵程伟董雄报
赵程伟,董雄报,洪 青
(桂林电子科技大学 商学院,广西 桂林 541004,E-mail:zcwei817@163.com)
基于Z-number 改进挣值法的工程项目成本进度集成控制分析
赵程伟,董雄报,洪 青
(桂林电子科技大学 商学院,广西 桂林 541004,E-mail:zcwei817@163.com)
挣值技术是项目实施中对项目进度费用进行评价与控制的重要工具。为提高挣值技术在不确定性环境中的适用性,引入Z-number模糊数,运用α截集法量化模糊数,提出一种新的模糊挣值模型。该模型不仅综合考虑了环境的模糊性、度量数据产生过程的不确定性及度量数据的可靠性,且能依据项目不同施工阶段特点,通过调节α的取值控制环境的模糊性,从而更贴近工程项目不同施工阶段的实际情况。并从数据角度与传统模糊挣值模型进行对比,验明了模型在工程管理实践中具有更强的适应性和更精准的预测评价。
工程项目;模糊挣值;Z-number模糊数;α截集模糊排序
在现代项目管理方法中,挣值法(EVM)既是最重要的管理方法,也是一种集成的控制方法。作为项目进度与成本综合控制与集成管理的方法,挣值法允许项目经理、项目管理人员等项目干系人在项目的全生命周期内,追踪和了解各监测时点项目的实施状态。为使挣值法对项目的评价与预测更加准确有效,国内外学者进行了多方面的研究并取得一定的研究成果。国外学者Lipke[1]针对传统挣值法进度绩效指标SPI的局限性,引入了挣得进度(ES)技术。Anbri等[2]提议使用其他的度量指标以克服传统SPI的限制。国内学者李南等[3]针对挣值法无法测评成本与进度风险的不足,提出设定缓冲区监控项目成本进度风险的动态变化。长青等[4]和赵峰[5]针对挣值管理方法从项目的整体角度对项目的绩效进行评价和控制而忽略了各项工作间的逻辑关系与实施情况的不足,提出应区分已获挣值来自关键路径还是非关键路径,分清偏差来源。戚安邦[6]从多要素集成的角度出发,将质量因素引入挣值管理方法中,实现质量、成本和进度的集成管理。上述学者改进了挣值对项目绩效评价与预测的准确性。但都建立在数据确定的基础上度量挣值,而未考虑在实际的工程项目管理实践中由于工程活动的不确定性或执行数据的不健全,使得项目管理者所收集到的数据本身就具有模糊性,进而造成挣值管理方法无法客观地反映项目的实际执行状况。
为了提高挣值法在不确定环境下对项目评价预测的准确性,戴育雷等[7]和王佳敏等[8]将模糊理论引入挣值法中。模糊数学与挣值法的结合,一定程度上提高了挣值法在模糊环境下的适用性。在活动总量不确定的情况下,活动的完成量由技术人员依据经验做出主观估计。然而,由于受到知识、经验、偏好、客观环境的复杂性等诸多因素的影响,致使其对问题的认知深度受到一定的限制,即判断活动的完工百分比时,其决策结果可靠程度和所包含的犹豫不确定程度是不同的。如技术人员给出某项活动完工百分比为20%,但“20%”可能是判断者在十分有把握的情况下给出的,即可靠程度非常高,也有可能在极度犹豫中做出决策,即决策结果的可靠程度非常低。而度量数据的可靠与否关乎挣值评价的准确性,因而在利用挣值技术评价项目时,考虑所获度量数据的可靠性是十分重要且必要的。但现有文献中少有将所获度量信息的可靠性考虑到模型中,Mostafa[9]虽然考虑了度量数据的可靠性,但不是专门针对工程项目,未依据工程项目的特点,考虑其在不同施工阶段本身所具有的模糊不确定性的差异。且其计算指标值(EAC等)及结果对比分析均以模糊数的形式表示,而不是以数值表示,结果不简单直观,造成实际使用中的不便。
鉴于上述分析,本文在前人研究的基础上,针对项目所获数据不健全或活动工作总量不确定的情况下,引入Z-number模糊数构建模糊挣值模型。该模型不仅考虑了不确定环境下,进度度量数据产生过程中的模糊性,而且还考虑了进度度量语言的可靠性程度,在此基础上,考虑到工程项目不同施工阶段模糊不确定性不同的特点,将环境的不确定性整合到模型中,运用α截集对模糊指标值进行量化,通过调节α截集的取值,可灵活地调控环境的模糊性,以更切合工程项目在不同施工阶段的实际情况,提出一种在工程项目管理实践中预测评价更准确的改进模糊挣值法。并通过与普通模糊挣值模型的对比分析,验证度量数据的可靠性对挣值评价结果的重要影响,进而体现模型更切合实际,更准确有效。
1 Z-number模糊模型分析
工程项目中,由于受到客观环境及技术条件等因素的影响,其实际的施工过程中,很多工程项目活动的工作量是未知的,或者说难以准确计量的。如桩基础工程中的人工挖孔灌注桩、钻(冲)孔灌注桩、预制桩的打桩,以及深基础的开挖等工程活动,由于其施工过程中对客观环境因素的敏感性较大,其整个工程活动工作量的多少高度依赖地质条件的好坏。对于这类工程活动,活动的完工百分比只能依据人的主观判断给出,而无法以数值的形式准确度量,因此在不确定性环境下普通挣值法失效。能否在不确定性较大的工程活动中有效使用挣值法控制项目的成本与进度,关键在于如何妥善处理度量数据所具有的模糊不确定性。
经文献查阅可知,目前处理不确定性的理论方法主要有概率与数理统计、灰色理论和模糊理论。3种方法各有其特点与适用范围,如概率论与数量统计适合解决数据多,样本大但规律不是特别明显的问题(即,大样本的不确定性问题)。灰色理论则适合处理数据少且无经验的小样本不确定性问题。而模糊理论则适合处理由人为引起的模糊不确定性问题(即,人认知过程的不确定性)。在不确定性较强的工程活动中,活动的完工百分比只能依据人的经验判断给出,因而所获度量数据带有人为认知的主观不确定性。为减少度量数据主观不确定性对挣值评价预测的影响,现有许多研究[7,8]引入模糊数对挣值法进行改造。但普通的模糊数(三角模糊数,梯形模糊数)只考虑了度量数据产生过程中的不确定性,忽略了度量数据本身的可靠程度,而度量数据的可靠与否直接影响挣值使用的准确性,因此在实际的使用过程中往往达不到令人满意的控制效果。受经验知识等因素的影响,人在对活动的完工百分比做出判断时,不仅仅是认知的过程存在不确定性,其认知的结果同样存在着不确定性。因此为加强不确定性环境下工程活动的进度与费用控制,必须将度量数据产生过程中的不确定性(认知过程不确定性)及数据自身的可靠程度(认知结果不确定性)考虑到挣值模型中。
基于 Z-number模糊数是以语言变量的形式度量活动的完工百分比,既符合实际操作习惯,又能充分利用专家的经验知识,且考虑了度量数据产生过程中的不确定性及数据自身的可靠程度,并将度量数据的模糊不确定性程度降至最低,因此本文引入 Z-number模糊数处理进度度量数据,对挣值法加以改进。
1.1Z-number模糊数
经典模糊集理论自从被Zadeh教授首次提出以来,就受到诸多学者的青睐,广泛应用于各个行业领域。在处理模糊不确定性方面经典模糊集具有较强的优势,但其忽略了信息的可靠性程度,为弥补其不足,模糊集的创始人Zadeh教授在经典模糊集的基础上,提出了 Z-number模糊集,与经典模糊集理论相比,Z-number模糊集考虑了信息的可靠性程度,因而能更好地表达现实环境中的不确定性[10]。Z-number模糊数[11]是一对有序的模糊数(Ã,B%)。其中第一部分Ã =(a1,a2,a3,a4),为一个梯形模糊数,在Z-number中起着模糊限制的作用,其隶属函数如下:

第二部分B%=(b1,b2,b3),为一个三角模糊数,在Z-number模糊数中用来说明第一部分(即Ã)的可靠程度,其隶属函数如下:
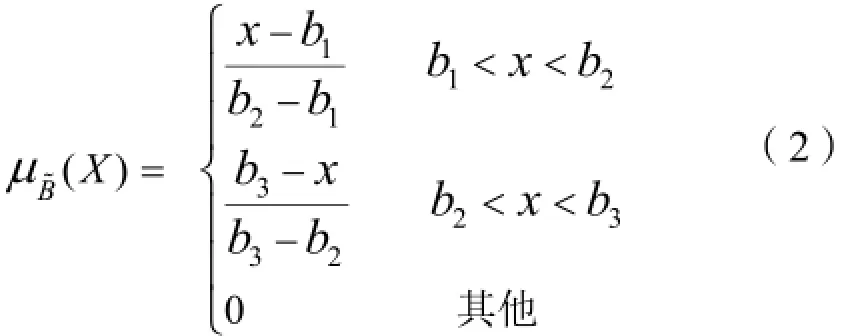
一个简单的Z-number模糊数如图1所示。
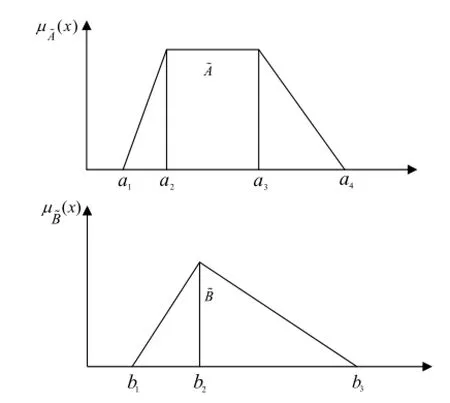
图1 一个简单的Z-number模糊数
1.2Z-number模糊数向经典模糊数的转化过程
Z-number模糊数不便直接用于量化计算,须将其转化成经典的模糊数。一个 Z-number模糊数可以写成Z=(Ã,B%),其中(Ã)起着模糊限制的作用,(B%)是模糊限制的可靠程度。定义
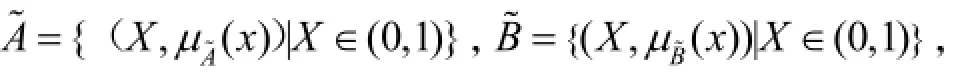
其中 μA为梯形模糊数,μB为三角模糊数。将Z-number模糊数转化为经典模糊数的方法较多,经对比选择,大多数方法计算过于复杂,考虑到方法的计算方便及可靠,本文采用 Bingyi Kang[12]提出的将 Z-number模糊数转化为经典模糊数的方法。具体操作步骤如下:
(1)将Z-number模糊数中表示可靠程度的部分(B%)转化成明确的数值,转化公式如下:
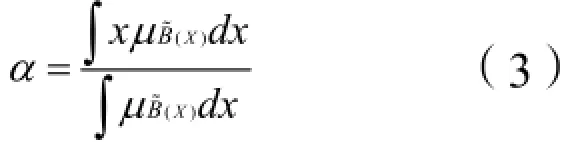
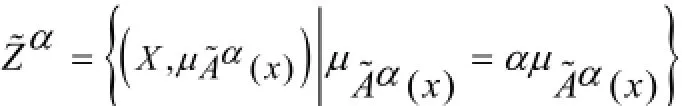
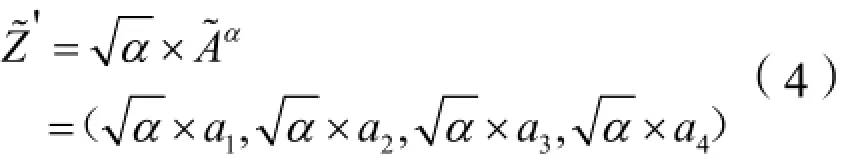
1.3模糊语言
模糊语言变量[7,12]由一个五元体表示为(X,T(x),L,G,M),其中X为语言变量名称,T(x)为语言集合,L是论域,G是语法规则,而M为语意规则。例如,一项不确定性活动的完成程度度量语言集T(x)为(非常低,低,不到一半,一半,高于一半,高,非常高),论域L取(0,1),语意规则M由论域上模糊集的隶属函数表示,采用梯形模糊数表示活动的进度度量值,如表1所示[9]。
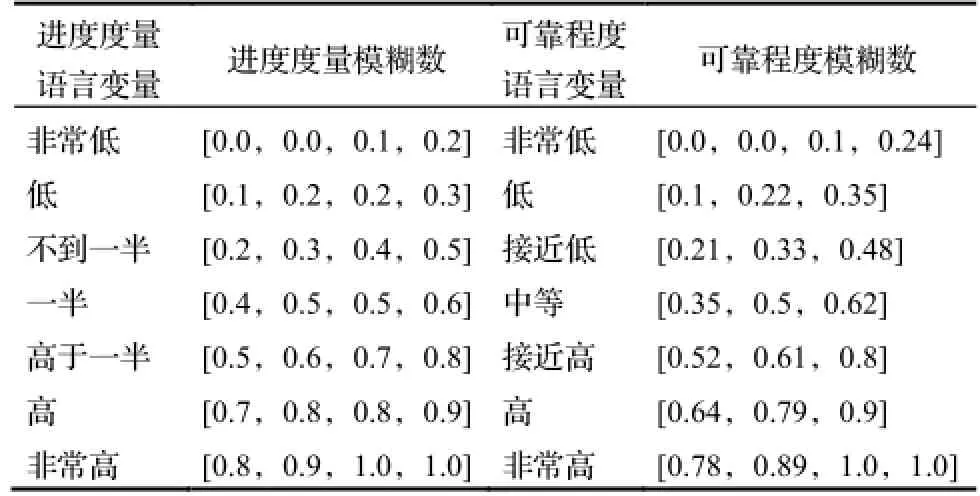
表1 模糊语言及对应的模糊数
表1描述了活动完工百分比的进度度量语言和度量语言的可靠程度及各自对应的模糊数。例如,一项活动的进度度量语言描述为非常高,活动进度度量语言的可靠程度为高,则根据表1,用Z-number模糊数表示为((0.8,0.9,1.0,1.0),(0.64,0.79,0.9))。
2 基于Z-number模糊数的改进挣值模型
2.1挣值指标的模糊化
挣值管理方法使用计划成本(PV)、项目实际成本(AC)和挣得值(EV)3个变量度量项目的进度与费用,从而达到对项目进度费用集成控制的目的。工程项目活动i的模糊挣值可表述为:
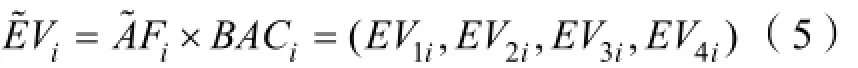
式中,ÃFi为活动i的实际完工百分比,且ÃFi为一个梯形模糊数;BACi为活动i的计划成本。整个项目的挣值EV由各项活动的挣值累加得到。其表达式为:
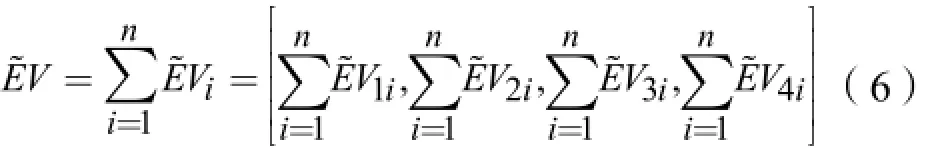
项目的成本进度绩效指标CPI和SPI,在模糊挣值法中用梯形模糊数可表示为:
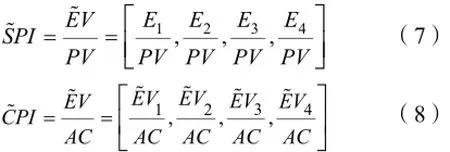
完工预测成本(EAC)表示检查时点后期的费用绩效按当前的费用绩效指标CPI进行,完工时所需的总成本。模糊成本预测指标可表示为:
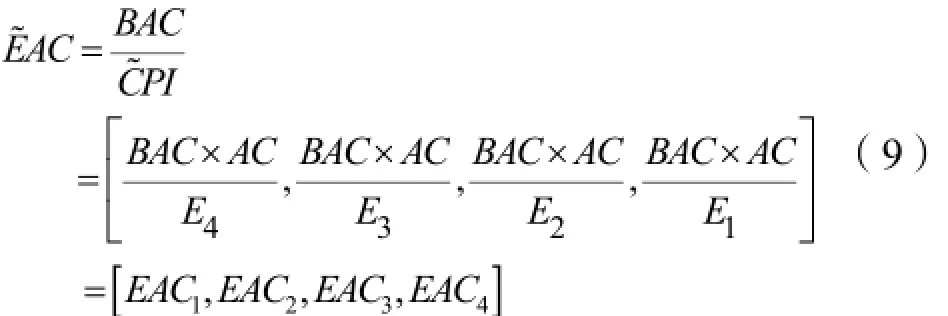
2.2基于模糊挣值的进度费用控制分析
由于模糊挣值指标值以模糊数表示,不便于直观的对比分析。为使项目经理等其他项目干系人直观便捷地通过相关挣值指标了解项目的实际进展情况,应选择恰当的方法量化模糊指标值。考虑到工程项目随着施工进度的推进,项目本身所具有的模糊不确定性是逐步递减的,为了充分反映这一特性,使本研究更贴近实际,本文应用α截集排序法量化模糊指标值。通过调节α的取值,模拟工程项目在不同施工阶段的模糊不确定性。
在α截集排序中,首先需要确定α值,且其值的确定需要综合分析项目所处施工阶段的主客观环境的复杂多变性。一般情况下,利用公司以往所收集的类似项目数据结合项目决策者对当前项目情况的综合分析确定α的具体值。也可采用层次分析法、模糊综合评价法、专家评价法等确定α的取值。在确知α值的基础上,对模糊挣值指标进行量化。梯形模糊数的α截集为:,则相对应的模糊进度绩效指数CPI% 和费用绩效指数SPI% 的α截集为:
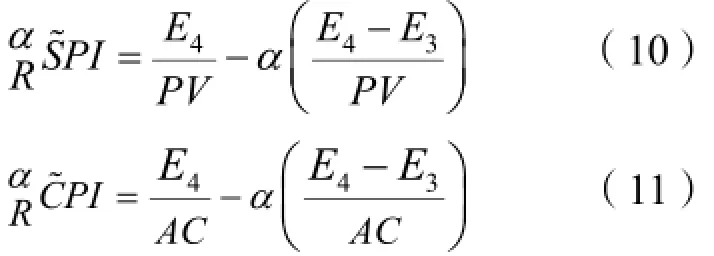
表2解释了用α截集法量化后的进度和费用指标及对应的项目实施状态。

表2 模糊CPI和SPI解释表
传统的挣值法中,完工预算(BAC)是指常规情况下完成项目所需的估算费用,并没有考虑风险事件发生时所需耗费的额外费用。由于工程项目具有复杂多变等特性,为应对由于工程变更或工程外部环境(材料价格或恶劣极端天气)变化等因素造成的工程费增加,国家规定必须为项目预留一定的风险费用,既预备费(RF)。留设预备费一定程度上降低了项目费用超支的风险。预备费RF与完工预算BAC之和为总预算费用TB。将完工估算(EAC)与 BAC和 TB进行比较获知项目完工时的费用情况。如表3所示。

表3 模糊成本预测指标解释表
综上,基于 Z-number模糊数的改进挣值模型的应用步骤如下:
步骤 1:依据先前制定的计划成本基线确定检查时点上的PV值,以及相关财务记录确定到检查时点各项工程活动的实际花费成本AC值。
步骤2:度量检查时点各项活动的完工百分比。由于工程活动具有模糊不确定性,难以用数值直接度量出活动完工百分比,因此首先由经验丰富的专家用语言变量表达出各项活动的完工百分比及所用语言变量的可靠程度。
步骤 3:依据表 1,将语言变量转化为相应的模糊数,获得 Z-number形式的进度度量数据。再用式(3)和式(4)将 Z-number形式的度量数据转化为普通模糊数。
步骤 5:根据工程所处施工阶段及客观环境因素综合地确定本检查时点工程项目外部环境的不确定性α的取值,并依据式(10)和式(11)量化模糊挣值指标值。
步骤6:将量化后的挣值指标值与表2和表3相对照,分析工程项目的实际执行情况。
3 示例分析
某工程项目计划在一年内完成,计划投资5000万元。在4月份检查时点,已经开工的工程活动主要有4项工序(工序1~4),项目各月份的累积计划成本及实际成本如表4所示。

表4 各月份累积计划成本和实际成本(单位:万元)
3.1模型的应用
应用基于 Z-number改进挣法评价项目的具体实施步骤如下:
(1)依据表4可知,在4月份检查时点PV= 1200万元,AC=1500万元。
(2)度量检查时点各项活动的完工百分比。各项工序的完工百分比如表5所示。

表5 检查时点各工序的进展情况
(3)依据表1,将表5中进度度量语言变量及可靠程度语言变量转化为相应的模糊数,获得Z-number形式的进度度量数据。再利用式(3)和式(4)将Z-number形式的度量数据转化为普通的模糊数,如表6所示。
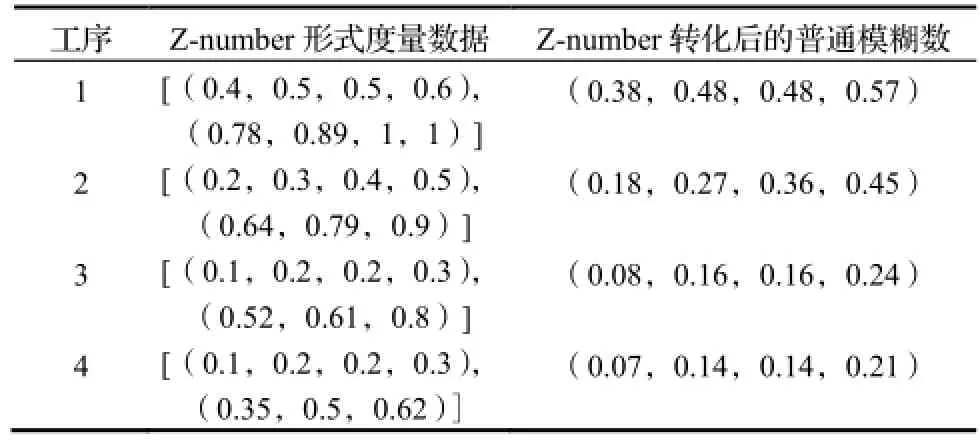
表6 工序的Z-number模糊数及转化后的普通模糊
检查时点各工序的挣得值为:

汇总各工序的挣值,获得项目的总挣的值为:
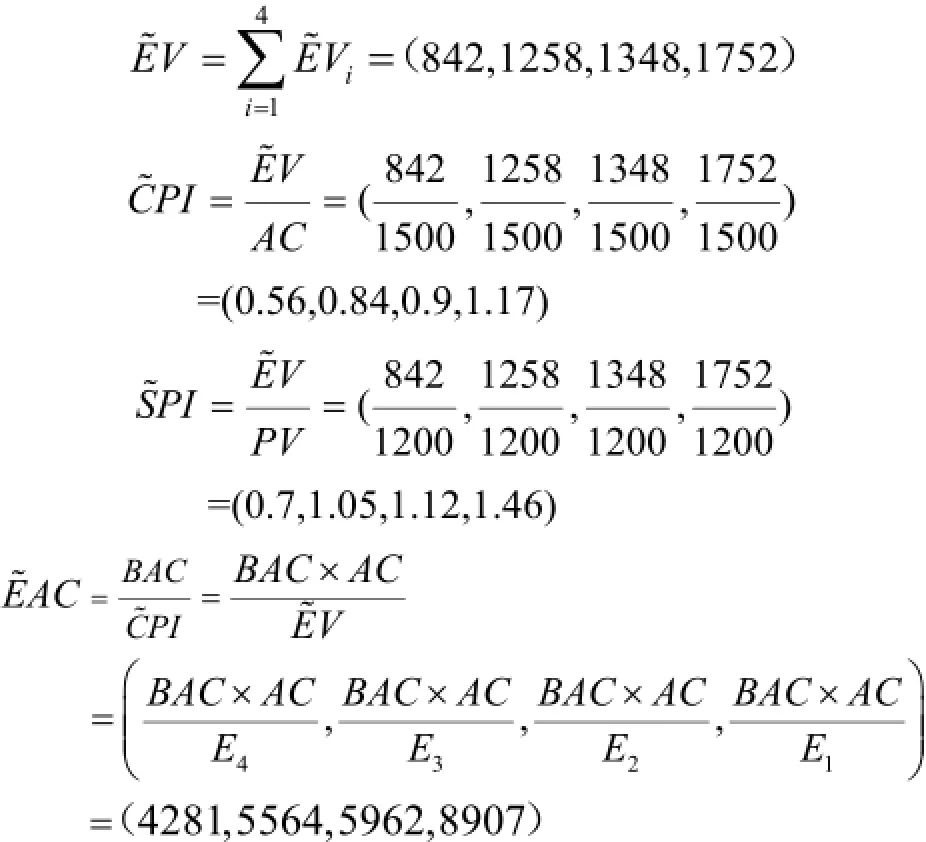
(5)结合工程的实际情况取 α=0.8,依据式(10)和式(11)量化模糊后的挣值指标值为:
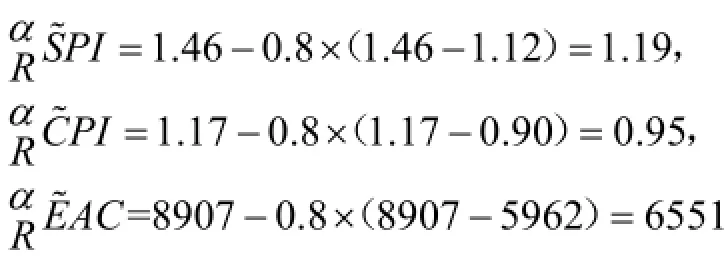
(6)确定检查时点工程项目的实际实施状态。若本案例中风险预备费为 1000万,则该项目可动用的总费用为:TB=BAC+RF=5000+1000= 6000。依据表 2,由于,因此在检查时点项目的进度提前可知在检查时点项目的费用超支。其费用的超支有可能是进度的提前引起的,项目管理人员应该仔细分析相关的原因,加以改正,以确保进度与费用均处于预定计划内。如按目前的实施状况发展下去,预计项目结束时所需的费用为 6551万,而依据表 3,因此项目完工时的实际费用将超出预算551万元。
3.2对比分析
为进一步验证度量语言自身的可靠程度对挣值法评价项目状态的重要影响,本文采用王佳敏[8]提出的方法计算本文案例中的各挣值指标值。计算结果分别为:由于均大于1,说明项目的进度提前且费用节约,项目处于较为理想的状态。同时由表3可知项目将在合同经费内完成,但需要动用672万的风险预备费。
进度度量语言的准确性将影响挣值指标对项目预测与评价的准确性。考虑进度度量语言可靠程度的不确定性后,项目的实际费用绩效指标项目的实际费用为超支,对比=1.11可知,由于进度度量语言可靠程度的不确定性引起了项目14.4%费用增长。1.38均大于1说明项目进度提前。但两者间的差异说明项目进度度量语言可靠度的不确定性造成了13.8%的项目进度延后。同时说明项目最终完工费用将超出项目总预算费用TB,度量语言可靠度的不确定性造成879万元的完工费用增加。上述数据分析可知,进度度量语言自身的可靠程度对挣值法评价及预测结果有着重大的影响,而从决策角度看,人在信息缺乏,模糊不确定的环境下,极有可能是在犹豫不决中给出决策结果,决策时的犹豫就造成了决策结果可靠性程度的不确定性,因此度量数据可靠性程度的不确定性是客观存在的。既然其客观存在,又从数据角度证明对挣值法评价及预测结果有着重大的影响,因此验证了本文提议模型更贴近工程项目的实际,从而所获预测评价结果更加准确可靠。
4 结语
在挣值法中,进度度量数据的可靠性将影响挣值量的大少,而挣值量的准确与否将影响挣值法对项目预测与评价的准确性。通过本文案例分析可知,由于进度度量语言可靠程度的不确定性引起了项目14.4%的费用增长,13.8%的进度延后。到项目完工时总费用超支14.6%。这些数据足以说明在不确定环境中,进度度量语言自身的可靠程度对项目进度费用的影响不容忽视。本文在现有模糊挣值模型的基础上,引入 Z-number模糊数对进度度量语言的可靠程度进行量化,结合α截集模糊量化排序,有效改善了不确定环境下挣值度量项目进度费用时,由于进度度量数据可靠程度的不确定性对挣值法评价与预测的影响,提高了挣值法在模糊环境中的实用性及对项目实施情况评价预测方面的准确性。同时改进后的模糊挣值法综合考虑并量化环境模糊性,度量数据产生过程中的模糊性及度量数据的可靠性,相比已有的模糊挣值模型而言,提议模型在不确定环境下,对实施中的工程项目进度费用等评价与预测更准确可靠。虽然模型在计算上相对复杂,但在实际应用中可通过计算机编程迅速得出计算结果,因此具有较强的可操作性和实用性。
[1] Lipke,W.Schedule is different[J].the Measurable News,2003,Summer:31-34.
[2] Anbari..Earned Value Method and Extensions[J].Project Management Journal,2003,34(4).
[3] 李 南,戴育雷,杨 莉.基于缓冲区和挣值分析的项目成本与进度风险预警[J].工程管理学报,2015(4):123-127.
[4] 长 青,吉格迪,李长青.项目绩效评价中挣值分析方法的优化研究[J].中国管理科学,2006,14(2):65-70.
[5] 赵 峰.基于关键路径的挣值分析法的优化研究[J].工业技术经济,2007,26(6):59-63.
[6] 戚安邦.多要素项目集成管理方法研究[J].南开管理评论,2002(6):70-75.
[7] 戴育雷,李 南,杨 莉.基于模糊理论的挣值管理方法[J]. 计算机仿真,2013(3):213-216.
[8] 王佳敏,陈永洲.不确定环境下工程项目改进模糊挣值法研究[J].工程管理学报,2012(6):57-61.
[9] Mostafa Salari.A novel earned value management model using Z-number[J].Applied Decision Sciences,2014,7(1).
[10] Bingyi Kang.A Method of Converting Z-number to Classical Fuzzy Number[J].Journal of Information & Computational Science,9(3):703-709.
[11] Zadeh,L.A.A note on Z-numbers[J].Information Sciences,2011(14):2923–2932.
[12] 胡宝清.模糊理论基础[M].武汉:武汉大学出版社,2004.
The Integrated Control of Cost and Progress of Construction Project Based on the Improved Earned Value of the Z-number Theory
ZHAO Cheng-wei,DONG Xiong-bao,HONG Qing
(School of Business,Guilin University of Electronic Technology,Guilin 541004,China,E-mail:zcwei817@163.com)
Earned value technology is an important tool for the evaluation and control of project schedule cost. In order to improve the applicability of the earned value technology in the uncertainty environment,the paper introduces the Z-number fuzzy number,and uses the method of the cut set method to quantify the fuzzy number,and proposes a new fuzzy earned value model. The proposed model not only considers the fuzziness of the environment,the uncertainty of the data generating process,and the reliability of the measurement data,but also can according to the characteristics of different stages of the project,control the vagueness of the environment by adjusting the α value,thus closer to actual situation in different stages of construction projects. Finally,from the perspective of data compared with traditional earned value model,and verify the proposed model in the practice of project management is more adaptable and more accurate evaluation.
construction project;fuzzy earned value;fuzzy numbers of Z-number;α-cut fuzzy ranking
TU723.3
A
1674-8859(2016)02-125-06 DOI:10.13991/j.cnki.jem.2016.02.024
赵程伟(1990-),男,硕士研究生,研究方向:工程项目管理;
董雄报(1954-),男,教授,硕士生导师,研究方向:项目管理,信息管理与信息系统,工业工程;
洪 青(1987-),女,硕士研究生,研究方向:工程项目管理。
2015-11-13.
