关于Hamilton原理*

梅凤翔李彦敏

（1.北京理工大学宇航学院，北京 100081）（2.商丘师范学院物理与电气信息学院，商丘 476000）

关于Hamilton原理*

梅凤翔1李彦敏2

（1.北京理工大学宇航学院，北京 100081）（2.商丘师范学院物理与电气信息学院，商丘 476000）

Hamilton发展了Lagrange分析力学，他对分析力学的主要贡献是一个原理—Hamilton原理和一个方程-Hamilton方程.本文给出Hamilton原理的经过史，包括Hamilton原著的表述，以及后人对这个原理的理解和发展.

分析力学，Hamilton原理，史料

引言

学科史研究是科学技术史研究的一个重要领域.分析力学史是力学史的一部分.国内外大多力学史中的分析力学部分内容较少，较粗，较旧，且有遗误，需要将分析力学史研究得较全，较细，较新，较准确.目前，国内外还没有人专门研究分析力学的学科史.本文作者期望对Lagrange力学，Hamilton力学，非完整力学，以及Birkhoff力学等的发生和发展给出历史的、客观的梳理与评价.

英国著名数学力学家Hamilton W R发展了Lagrange分析力学，他基于积分变分原理在分析力学发展中做出了非常重大的贡献，主要体现在给出了Hamilton原理和Hamilton正则方程.本文在第一手资料的基础上，给出Hamilton原理的经过史，包括Hamilton原著的表述，以及后人对这个原理的理解，并进一步阐述了Hamilton原理的意义与发展.

1 Hamilton原理

1.1 Hamilton的贡献

Hamilton W R（1805—1865），汉译哈密顿，英国数学家，物理学家，力学家.他在分析力学方面的贡献是两篇长文：《论动力学中的一个普遍方法》（On a generalmethod in dynamics，1834）和《再论动力学中的普遍方法》（Second essay on a general method in dynamics，1835）其中给出正则方程和Hamilton原理.

1.2 Hamilton的原著

Hamilton在第二篇长文中写道［1］：

“这个函数S已在第一个工作中表述为形式

其中公式中的符号T和U有通常意义.必须注意，当S用这个定积分表示时，为消去它的变分条件（如果给定初始和终了位置和时间）恰好是由Lagrange给出的运动微分方程.因此，这个定积分S的变分具有双重性质：当端点位置当作固定的，它给出对任何变换坐标的运动微分方程；当端点位置当作变动的，它给出这些微分方程的积分.”

［注］以上文字就是Hamilton对他的原理的表述，未明显指出δS=0.

1.3 对Hamilton原著的理解和表述

1）Полак对上述双重性质给出如下表达［2］

2）Jacobi的表述

Jacobi C G J（1804—1851）在其《动力学讲义》第八讲“Hamilton积分与动力学方程的第二La-grange形式”中写道［3］：

“代替最小作用量原理，可提出另一原理，也是使某一积分的一次变分为零，由此可比最小作用量原理更简单地得到运动微分方程.……Hamilton是第一个由这个原理出发的.我们利用这个原理建立Lagrange在分析力学中给出的运动方程形式.首先设Xi，Yi，Zi是函数U的偏导数；进而设T为活力之半

此时新原理表示为方程

这个新原理比最小作用量原理更普遍，因为这里U可显含t，而最小作用量原理不含t.…”

“完全表示的新原理这样表述：

如果给定系统在初时刻t0和给定末时刻t1位置，那么为确定真实发生的运动就有方程这里积分从t0至t1，U是力函数，可包含时间t，而T是活力之半…”

［注］Jacobi将Hamilton原理表述清楚了，而且U可含时间t，是一进步.

3）Moiseev的评介

Moiseev N D（1902—1955）为苏联力学史著名专家，他在《力学发展史》中有如下段落［4］：

“…Hamilton基于积分变分原理在分析力学发展中做出了非常重大的贡献，这个原理称为Hamilton-Ostrogradsky原理，稍晚一些，Ostrogradsky独立于Hamilton，在其工作中找到并研究了这个原理，并指出这个原理有可能应用于比Hamilton更多更广一类力学问题.”

“首先，Hamilton将Maupertuis最小作用量原理中研究作用量作为轨道始、末点坐标的函数.这个函数在光学研究中起重要作用，Hamilton称其为“特征函数”

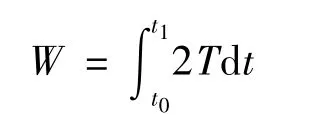
它不是别的，就是Lagrange作用量.Hamilton还引出一个重要函数

他称其为主函数.这个函数表示Hamilton作用量.Hamilton建立了函数W和S之间的关系，并借助它建立起基于作用量S稳定的原理的完整动力学系统.”

“在这些表达式中T表示系统的动能，而U为系统的力函数.Hamilton仅研究带不依赖于时间的约束的保守系统.”

“在两个工作中建立的一般原理表述如下.

对系统的任何轨道段，作用量（主函数S）取稳定值（驻值），如果作为比较的临近曲线在同样时间有同样的端点A和B.因此，Hamilton假设系统的总能在相邻轨道上可以不同，而在最小作用量原理中对所有比较轨道这个量是一样的.”

“因此，Hamilton稳定作用量原理的解析表达如下

进而，Hamilton证明他的函数W和H满足某个微分方程组，方程组的解与下述偏微分方程

的解相关，其中所谓“Hamilton函数”H是广义坐标q1，q2，…，qn和广义动量p1，p2，…，pn的下述函数

Hamilton建立了方程（3）的解与正则形式运动常微分方程组的解的联系，其中n为系统的自由度数.

现时以Hamilton名字命名的这个原理和运动的正则方程（4），不仅是许多力学现象，而且是许多物理过程研究的工具.”

“Jacobi对这个理论有兴趣，于1837年继续发展了Hamilton原理，以及由此原理导出的运动微分方程.但是，Jacobi给出这个复杂理论具体应用的两个例子：他研究了质点在受到两个中心牛顿引力作用下的运动问题，以及质点在光滑椭球面上无外力作用条件下的运动问题.至于第一个问题早在100年前已由Euler解决，而后不止一次地由其他人借助运动的常微分方程解决了.第二个问题，Jacobi借助Hamilton-Jacobi偏微分方程的复杂工具由他首先解决，但没有原则上困难.”

［注］1）以上段落提到Ostrogradsky和Jacobi 在Hamilton原理方面的工作.2）关于对Jacobi定理工作的评价与Arnold的评价相距甚远.Arnold指出“Jacobi定理将常微分方程组的求解化为求偏微分方程的完全积分.这样由简“化”繁却提供了解决问题的有效方法，这是令人惊奇的.然而这却是求精确解的最有力的方法，而Jacobi解出的许多问题用别的方法是解不出来的.”［5］

4）Appell的表述

Appell在其著作第二卷第484节“Hamilton原理”中有如下表述：［6］

“前一章已经看到，在系统无摩擦下，每一时刻t，对这一时刻为约束允许的可能位移δx，δy，δz有下述形式的方程

这个结果可表示为以下形式，由此可组建Hamilton原理.

给定系统在时刻t0和t1的位置P0和P1.在系统由位置P0到位置P1在给定力和约束力作用下的真实运动中，不同点的坐标x，y，z是时间的函数，这些函数在给定的时刻t0和t1满足约束方程.设x+ δx，y+δy，z+δz是时间的任意函数，它们无限接近相应真实运动的函数x，y，z.这些函数，如x，y，z也在时刻t0和t1满足约束方程.因此，δx，δy，δz是时间的无限小函数，在时刻t0和 t1变为零，由在这个间隔中为约束允许的位移所确定.用T=表示系统在真实运动中的动能，用δT表记当x，y，z得到上述变分δx，δy，δz时，这个能的变分.Hamilton原理在于，积分

在满足所指条件下对所有值δx，δy，δz，等于零.积分号中和号∑对约束反力外的所有给定力.为证明ΔS等于零，注意到

分部积分，上述积分写成形式

因δx在边界上为零，其中积分出来的部分为零.因此，变换积分的所有项，最终得到

由方程（5）知，δS等于零，因为δx，δy，δz是时刻t具有约束允许的位移.”

在第485节“由Hamilton原理导出Lagrange方程”中写道：

“上面的计算不能应用于非完整系统，因为对这类系统等式dδq=δd q不对.”

“特殊情形，当施加力沿坐标轴的分量等于依赖坐标和时间的函数U的偏导数.在此情形虚功之和

是函数U的全微分δU，取t为常数.此时有

而Hamilton原理表述如下.如果给定系统在时刻t0和t1的位置，那么积分

在由真实运动向为约束允许的无限接近的任何运动过渡时，它的变分为零.”

［注］1）Appell由动力学普遍方程（5）导出原理

它是一般完整系统的Hamilton原理.2）Appell指出原理的前提是无摩擦运动，无摩擦约束后来发展为理想约束.3）Appell指出这个原理不适合非完整系统.

5）Whittaker的表述

Whittaker在其著作第99节“完整保守系统的Hamilton原理”中写道［7］：

“研究任何完整保守动力学系统，其在任何瞬时的位形由n个独立坐标（q1，q2，…，qn）来确定，并令L是表征其运动的动势.令n维空间中一给定弧AB表示系统的部分轨道，而令CD为一邻近弧，它不一定是系统的轨道；然而，当然可能使CD是系统遵从附加约束的轨道.令t是代表点（q1，q2，…，qn）在AB上占据任何位置P的时间.假设CD上每个点与时间的某个值相关联，那么在CD（或者使CD是其部分的弧）上存在一点Q，它对应与P一样的同值t.……

用δ表示变分，用这个变分使AB上的一点到CD上的点，与时间同值相关，用t0，t1，t0+Δt0，t1+ Δt1分别表示对应端点A，B，C，D的t值，而用LR表示在两弧上任意点R的函数L的值.

如果构成积分

沿弧AB和CD上的差，就是但是

类似地有

而因此有

现在假设C与A，D与B重合，与C和D关联的时间分别是t0和t1，那么Δq1，Δq2，…，Δqn，Δt在A和B是零，而最后一个方程成为

这表明对真实轨道的任何部分AB，与和真实轨道有同样端点，时间同样端值的邻近路径CD相比较，积分有稳定值.这个结果称为Hamilton原理”.

6）Suslov的表述

Suslov在其著作第201节“Hamilton形式的稳定作用量原理”中写道［8］：

“取系统两个可能位置A0和A1，它们可用直路联结.设系统沿直路从A0到A1在时间间隔t1-t0内完成，其中t0和t1表示系统在A0和A1的时间.研究积分

比较这个积分在系统沿直路运动的值和系统沿旁路运动的值，这个旁路也由初始位置A0到终了位置A1，并设系统沿任何旁路由A0到A1与直路运动同时开始并同时终了.此时有，直路的积分值W与旁路的相比较是稳定的，换言之，对直路的积分（7）的一次变分为零.在变分时需要注意所有以上所指限制

（1）系统的约束不能破坏；

（2）所有旁路在时刻t0同时开始并在时刻t1同时结束；沿直路的运动也在这些时刻开始与结束；

（3）系统的起始和终了位置对所有路径是一样的.

…对函数W取变分，有

为变换第一项，注意到当时间不变分时，变分与对时间的微分是可交换的.实际上令是函数qσ的变分值，有

两端求导数，有

于是得到

按条件t=t0和t=t1坐标变分qσ等于零，因此有

据所指对函数W的变分表达式（8），可得到下述形式

因沿直路的运动满足方程（7），那么上式中积分号下函数等于零，这就证明了

积分（7）的所证性质导出了Hamilton原理.积分W本身通常称为Hamilton作用量而原理本身可表述为：Hamilton作用量沿直路由系统给定的初始位置到终了位置与在同样位置间发生的沿旁路的作用量相比较具有稳定值，如果系统沿所有路径在同样时间间隔t1-t0内完成…”.

［注］1）Suslov由Lagrange方程证明了Hamilton原理.2）Suslov给出例子证明Hamilton原理不适合非完整系统.

7）Lurie的表述

Lurie在其著作第十二章“力学的变分原理”中写道［9］：

是时间的函数，它们是受有完整理想约束的质点系在真实发生运动中的广义坐标.主动（给定）力有势.将说，函数（1）的总合确定的真实路径，而∞n个无限接近真实位形为约束允许的任何一个

确定邻近路径，其中变分δqs是时间的任何无限小可微函数.

用L表记动势，即动能与势能之差.在真实路径上

是时间的某个已知函数.在过渡到∞n邻近路径中的一个，动势的变分等于

这里已用法则《δd=dδ》.

［注］Lurie在式（13）之后利用 Lagrange方程导出了δS=0.

1.4 Hamilton原理的极值性质

1）Lurie的论述

Hamilton原理指出δS=0，那么这个极值是极大还是极小呢？Lurie证明，如果积分区间充分小，那么在定常约束下，Hamilton作用量具有极小值.

2）陈滨的论述

陈滨在其著作中给出Hamilton作用量有强极小值和弱极小值的充分条件［10］.

2 Hamilton原理的推广

2.1 对完整系统的推广

Appell给出原理对完整保守系统的推广

写成广义坐标形式，有

文献［11］给出一类新型积分变分原理.在m次速度空间中，如果力学系统受有完整理想约束，并且所有主动力有势，势函数为V=V (t，qs)，则系统的运动使泛函

在系统的真实运动轨道上取驻值，其中

当m=0时给出Hamilton原理.

2.2 对非完整系统的推广

1）Chetaev型非完整系统

将广义有势情形的d′Alembert-Lagrange原理

写成形式

将其对t由t0至t1积分，并注意到端点条件，得到

Hölder形式也叫Voronets形式.

［注］1）文献［12］称Hölder形式为Voronets形式.2）Suslov（1857-1935）是老师，Voronets（1871-1923）是学生，关于Hamilton原理应用于非完整系统，两人有过争议，而实际上他们两人都没有错.

2）Vacco动力学系统

Goldstein在其《经典力学》中指出，对受有约束

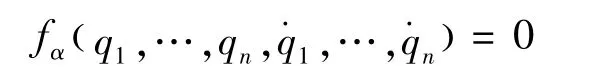
的系统，Hamilton原理可写成［14］：

由此导出方程

［注］1）所得方程为Vacco动力学方程.2）文献［15］指出，上述原理是数学变分问题，导出的方程在力学/物理上是不正确的.

3 Hamilton原理的意义与进一步发展

3.1 Hamilton原理的意义

Полак指出“很难指出物理-数学科学的其他领域，把抽象的数学研究与具体的物理内容如此深刻地结合起来.力学的变分原理不仅是自然和技术的最复杂、多方面问题的精美工具，而且运动规律的独特表达形式远远超出了经典力学的限制.”［2］Hamilton原理正是这样的.

Hamilton原理是力学的基本原理，并且它把原理归结为更一般的形式.同时它与坐标选择无关，因此，更具有普遍性并在多方面应用上更为方便.例如，应用Hamilton原理来推导Lagrange方程和正则方程更为简单更为自然.这不单是反映数学逻辑推理上的巧妙，主要是反映了原理更深刻地揭示了客观事物之间紧密的联系［16，17］.

对Hamilton原理在近似计算上的应用，文献［17，18］给出很好的例子.文献［10，19］将Hamilton原理应用于耦合RLC电路、柔性多体以及刚柔耦合系统动力学.

3.2 Hamilton原理的进一步发展

1927年Birkhoff在其著作《动力系统》中提出一类新型积分变分原理和一类新型运动微分方程.1983 年Santilli将这些结果推广到包含时间的情形［20］.那个原理可称为Pfaff-Birkhoff原理［20，21］，有形式

则给出Hamilton原理

文献［21，22］研究了Birkhoff系统动力学.文献［21］还由Pfaff-Birkhoff原理导出了Pfaff-Birkhoff-d′Alembert原理.

4 结语

⑴本文给出有关Hamilton原理的一些史料，包括Hamilton原著的表述，后人的理解与发展.

⑵Hamilton给出了Hamilton作用量S，但未明确地给出ΔS=0.Jacobi明确给出了原理ΔS=0.Ostrogradsky也研究了这个原理，因此，俄国人称原理为Hamilton-Ostrogradsky原理.

⑶Hamilton原理的前提是：约束是双面理想完整定常的，力是有势的且不含时间，可比较路径与真实路径有同样始、终点并在同样时间间隔内完成.这个原理可推广到完整非保守系统和非完整系统，但一般说已不再是稳定作用量原理.

⑷Hamilton原理推广到Pfaff-Birkhoff原理，经历了90多年，为Birkhoff系统动力学打下了理论基础.

⑸文献［2］指出，文献中大量出现的“原理的证明”无疑是不合理的，原理无需证明.当然，人们开始时总是希望用已有的知识来验证新知识的正确性，因此就有了Appell用动力学普遍方程，Whittaker 用Lagrange方程来验证Hamilton原理的经历.

1 Hamilton W R.Second essay on a general method in dynamics.Phil.Trans.Roy.Soc，1835，1：95～144

2 ПолакЛСВаРициοнныеПринципыМеханики.Москва：ГИΦМЛ，1959

3 Jacobi C.Vorlesungenüber Dynamik.Berlin：Clebsch，1866

4 МоисеевНД.ОчеркиΡазвитияМеханики.Москва：ΝМУ，1961

5 Arnold V I.MathematicalMethods of Classical Mechanics. New York：Spriger-Verlag，1978

6 Appell P.Traitéde Mécanigue Rationnelle，TⅡ.Sixème Édition，Paris：Gautnier-Villars，1953

7 Whittaker E T.A Treatise on the Analytical Dynamics of Particles and Rigid Bodies.Fourth Edition.Cambridge：Cambridge Unir.Press，1952

8 СуслοвГК.ТеοретическаяМеханика.Москва：Тοстехиздат，1946

9 ЛуръеА И.АналитиЧескаяМеханика.Москва：ГИФМЛ，1961

10 陈滨.分析动力学，第二版.北京：北京大学出版社，2012（Chen B.Analysis of dynamics，Second edition. Beijing：Peking University Press，2012（in Chinese））

11 赵跃宇.力学的新型积分变分原理.力学学报，1989，21（1）：101～106（Zhao Y Y.New integral variational principle ofmechanics.Acta Mechanica Sinica，1989，21 （1）：101～106（in Chinese））

12 НовосёловВС.ВариационныеМетдывМехлнике. ИЛУ，1966

13 梅凤翔.分析力学，下卷.北京：北京理工大学出版社，2013（Mei F X.Analysis ofmechanicsⅡ.Beijing：Beijing Institute of Technology Press，2013（in Chinese））

14 Golastein H.Poole G，Safko J.Classical Mechanics. Third Edition，Beijing：Higher Education Press，2005

15 Papastravridis JG.Anaiyticai Mechanics.New York：Oxford Unir.Press，2002

16 梅凤翔，刘桂林.分析力学基础.西安：西安交通大学出版社，1987（Mei FX，Liu G L.The foundation ofanalytical dynamics.Xi＇an：Xi＇an Jiaotong University Press，1987（in Chinese））

17 朱照宣，周起钊，殷全生.理论力学，下册.北京：北京大学出版社，1982（Zhu ZX，Zhou Q Z，Yin QS.TheoreticalmechanicsⅡ.Beijing：Peking University Press，1982 （in Chinese））

18 黄昭度，钟奉俄.工程系统分析力学.北京：北京高等教育出版社，1992（Huang ZD，Zhong F E.Analytical dynamics of engineering system.Beijing：Higher Education Press，1992（in Chinese））

19 丁光涛.三种耦合RLC电路的Lagrange函数和Hamilton函数.动力学与控制学报，2014，12（4）：304～308 （Ding G T.Lagrangians and Hamiltonians of three coupled RLC circuit.Journal of dynamicsand control，2014，12（4）：304～308（in Chinese））

20 Santilli RM.Foundations of Theoretical MechanicsⅡ. New York：Springer-Verlag，1983

21 梅凤翔，史荣昌，张永发等.Birhoff系统动力学.北京：北京理工大学出版社，1996（Mei F X，Shi R C，Zhang Y F etc.Dynamics of Birkhoff system.Beijing：Beijing Institute of Technology Press，1996（in Chinese））

22 ГалиуллинАС，ГаораровГГ，МалайшкаРП，Хван АМ.АналитическаяДинамикаСистемГельмгольца，Биркгоора，Намьу.Москва：УФН，1997

*The project supported by the National Natural Science Foundation of China（10932002，11272050，11372169）

E-mail：hnynmnl@163.com

ON HAM ILTON PRINCIPLE

Mei Fengxiang1Li Yanmin2

（1.School of Aerospace，Beijing Institute of Technology，Beijing 100081，China）（2.Department of Physics and Information Engineering，Shangqiu Normal University，Shangqiu 476000，China）

Hamilton WR developed Lagrange analyticalmechanics，and hismain contribution to analyticalmechanics is a principle of the Hamilton principle and an equation of the Hamilton equation.The developing history of the Hamilton principle is given in this paper，including the expression of the Hamiltonian original version，the understanding of other researchers on the principle aswell as its development.

analyticalmechanics，Hamilton principle，historicalmaterialsReceived 10 December 2014，revised 28 December 2014.

10.6052/1672-6553-2015-015

2014-12-10收到第1稿，2014-12-28收到修改稿.

*国家自然科学基金资助项目（10932002，11272050，11372169）

E-mail：hnynmnl@163.com