自适应扩散算法的误差性能分析*

郭　超，张政保，姚少林，刘广凯

(1.军械工程学院 信息工程系，石家庄 050003；2.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003)

YAO Shaolin,ZHANG Zhengbao,XU Xin,et al.Distributed cooperative spectrum detection algorithm based on diffusion strategy[J].Telecommunication Engineering,2015,55(12):1401-1406.(in Chinese)



自适应扩散算法的误差性能分析*

郭超1，张政保1，姚少林2，刘广凯1

(1.军械工程学院 信息工程系，石家庄 050003；2.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003)

为了分析分布式协作频谱感知认知网络中融合矩阵、步长等参数对自适应扩散算法的影响，对检测量估计误差性能进行了研究。给出了自适应扩散算法检测量的通用迭代公式，分析了检测算法的数据处理流程；推导了检测量估计误差向量的迭代表达式，利用网络瞬时均方偏差性能和各节点的稳态均方偏差性能评价融合矩阵参数对算法的影响。结果表明，不同的融合矩阵选取原则影响算法的检测性能，可以采用检测量误差估计的方法对算法参数进行研究。

认知无线电；协作频谱感知；分布式估计；扩散策略；共识策略；误差性能分析

1　引　言

认知无线电网络(Cognitive Radio Network,CRN)中，认知用户(Secondary User,SU)可以采用多节点协作的方式克服环境中干扰、衰落、阴影等影响，发现频谱空洞，避开对主用户(Primary User,PU)信号的干扰。频谱环境是时变的，分布式网络在线学习方法能够利用SU的观测信息学习得到PU信号统计信息，实现对频谱空洞的实时检测[1-3]。

文献[4]将基于共识的分布式协作频谱感知策略应用到有移动节点的认知无线电网络，提出认知网络中节点的最大自由度预测模型，利用共识协作策略平均各认知节点的能量值，较好地解决了节点移动对PU信号检测的影响。文献[5]提出基于加权平均共识的分布式协作频谱感知策略，信噪比更高的认知节点的检测值获得更大的融合权重，有效提高了检测性能。两篇文献的共同缺陷在于频谱感知过程被分为检测量获取和融合两个阶段，经过多次迭代过程达到检测量的一致，检测量的收敛过程会带来巨大的检测时延，协作检测实时性较差。文献[6]采用扩散策略解决自适应网络的分布式估计问题，网络节点通过与相邻节点通信，通过自适应更新过程和融合更新过程，能够有效估计出最优的状态量信息。文献[7]对自适应网络中基于共识策略和扩散策略的分布式估计性能进行了比较，扩散网络的收敛速度更快，节点的瞬态和稳态均方偏差更小，得出扩散策略优于共识策略的结论。

笔者在文献[8-9]中提出了基于扩散策略的分布式协作频谱检测算法和分布式实时频谱检测算法，对算法基本原理进行了推导，得出了检测量估计的递推表达式。本文在此基础上考虑基于扩散策略的分布式协作频谱检测算法的检测量误差性能，研究了融合矩阵对扩散算法性能的影响，以检测量估计误差的均方偏差作为衡量标准，仿真验证了4种不同融合矩阵的检测量误差性能。

2　网络模型及信号检测模型

考虑一个由K个SU构成的分布式CRN，它可以描述为无向图模型G=(V,ξ)，其中节点集合V={1,2,…,K}，边集ξ={(i,k)|i,k∈V,i≠k}为SU在单跳通信范围内的无序节点对，邻集Nk={l|(l,k)∈ξ}⊂V为节点k的单跳通信相邻节点集，集合Nk中元素的个数nk为节点k的度。

在CRN中，SU对PU信号的检测可以看作是二元检测模型：

(1)

式中：ti(n)表示认知节点i在第n个感知阶段的检测量；γ表示检测门限；H0表示检测量小于门限值，PU信号不存在；H1表示检测量大于门限值，PU信号存在。

3　基于扩散策略的分布式协作算法

扩散策略能用于解决分布式网络节点状态估计、优化等问题[10-14]。认知网络中，SU需要通过相邻节点的检测量信息交换达到分布式协作的目的。协作过程中，每个SU都必须根据一定的信息交换策略与相邻节点交换当前时刻检测量信息，然后按照交换策略估计出当前时刻的检测量估计值，最后各个节点独自根据该估计值做出最终的检测判决。

节点为了估计出各自检测量的最优值就必须使CRN的全局代价函数最小[8]:

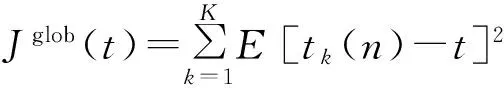
(2)

认知网络的目标就是SU采用分布式行为实时估计出检测量的最优值。ATC扩散算法和CTA扩散算法是解决方程(1)的两种不同算法。

引入非负系数{al,k,cl,k}满足

C1=1，AT1=1。

(3)

式中：C为右随机矩阵(矩阵元素的行和为1)；A为左随机矩阵(矩阵元素列和为1)。其等价形式为，对于所有k=1,2,…,K,满足

(4)

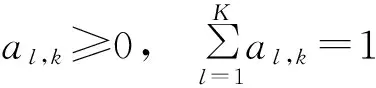
(5)

ATC扩散算法和CTA扩散算法的迭代表达式分别为

(6)

(7)

式中：μk为节点k的正的步长参数，步长参数固定能够赋予认知节点学习能力，检测量估计值可以跟随环境的变化而改变。矩阵A和C的选择原则影响认知网络各节点的检测性能。

3.1算法的数据处理过程

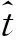
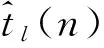
图1ATC扩散和CTA扩散算法

Fig.1 ATC diffusion algorithm and CTA diffusion algorithm

3.2融合矩阵

融合矩阵的选取原则决定了网络收敛速度和融合性能。在CRN拓扑结构未知的情况下，SU无法获得全局节点最大自由度以及节点数目的信息，而SU只能得到本节点以及相邻节点的自由度情况，因此融合矩阵的选取原则必须建立在单个节点能够获取的拓扑信息上。表1列出了融合矩阵的选取原则。

表1融合矩阵选择[9]

Tab.1 Selection off usion matrix

选取原则融合矩阵A的元素矩阵A的类型平均准则(Averagingrule)al,k=1/nk,ifl∈Nkorl=k0,otherwise{左随机拉普拉斯准则(Laplacianrule)al,k=1/nmax,ifl∈Nk1-(nk-1)/nmax,k=l0,otherwise{对称且双随机Metropolis准则al,k=1/max{nk,nl},ifl∈Nk1-∑l∈Nk{k}al,k,k=l0,otherwise{对称且双随机相对自由度准则(Relative-degreerule)al,k=nl/∑m∈Nknm(),ifl∈Nkork=l0,otherwise{左随机

可以看出，几种融合矩阵构造的方法很大程度上依赖于节点的自由度，与每个节点相通信的相邻节点的数目影响融合权重。由于没有考虑到网络中各节点噪声水平的不同，这几种权重选择方案在不同程度上降低了自适应网络中节点的检测性能。一些节点可能比其他节点噪声更大却有更多的邻居节点，因此融合矩阵的取值原则必须考虑认知节点的信噪比和自由度两种信息。

4　性能分析

本节分析扩散LMS算法的两种形式，即ATC扩散算法和CTA扩散算法。采用一种通用的算法形式表示扩散LMS算法(ATC和CTA算法是两种特例)：

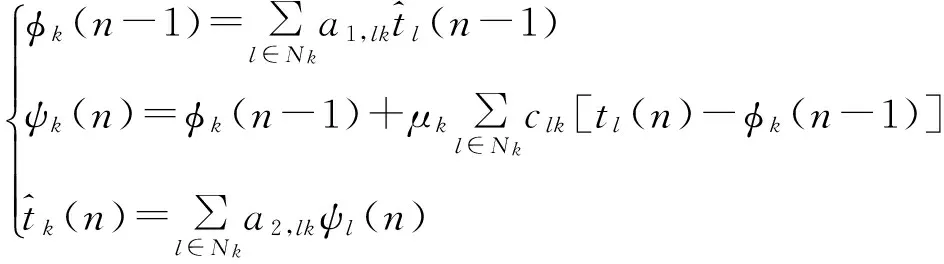
(8)

标量{a1,lk,clk,a2,lk}为非负实系数，是K×K融合矩阵{A1,C,A2}中(l,k)对应的元素，矩阵{A1,A2}为左随机矩阵，C为右随机矩阵。不同的矩阵选择，对应不同的合作模式。若A1=IN,A2=A，则对应自适应ATC实现；若A2=IN,A1=A，则对应自适应CTA实现。

4.1模型假设

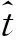
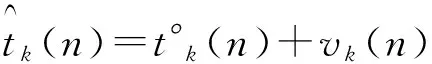
(9)

采用扩散算法的SU可以实时估计出各个节点的检测值，认知节点的环境适应能力决定了每一时刻所有节点的检测量估计值并非完全相同。为了衡量各个节点检测量的估计性能，定义节点k的检测量估计误差。利用式(8)，定义误差

(10)

认知网络在n时刻的误差向量为

(11)

引入矩阵

M=diag{μ1,…,μK}，

(12)

(13)

(14)

引入列向量

s(n)=col{v1(n),v2(n),…,vN(n)}，

(15)

(16)

由式(8)可以得出如下关系：

(17)

检测量估计误差向量的递归表达式为

(18)

4.2误差性能

为了衡量扩散算法估计得到的检测量的误差性能，定义本地节点的均方偏差MSDk和认知网络的均方偏差MSDnetwork。瞬时性能可以体现在不同时刻检测量估计值随检测环境的适应过程，稳态性能可以体现节点在所处认知网络中的性能表现。

定义节点k在n时刻的本地均方偏差MSDk(n)和认知网络的均方偏差MSDnetwork(n)：

(19)

(20)

认知节点检测量估计值达到稳定时的均方偏差MSDk为

(21)

5　仿真分析

本节采用Matlab仿真工具，利用蒙特卡洛仿真实验方法，对采用不同融合矩阵时，两种扩散算法得到的检测量的误差性能进行仿真实验。仿真采用10节点认知网络，其拓扑关系和信噪比信息如图2所示。仿真实验中，PU信号为高斯白噪声信道下的QPSK信号，其基带码元速率为2kb/s，载波信号为10kHz，数据采样速率为50kHz。SU采用最大最小特征值(Maximum-MinimumEigenvalue,MME)检测算法得到各个节点的检测统计量，并把该数据作为多认知节点的协作初始信息。

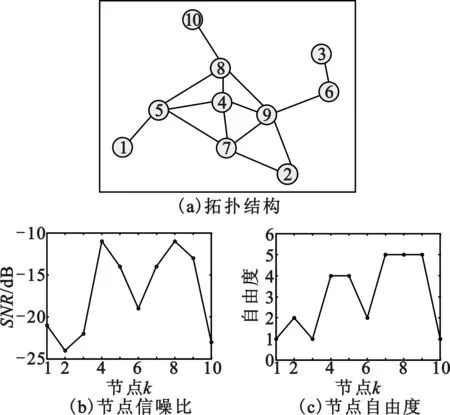
图210节点网络拓扑结构

Fig.2 10-nodenetworktopology

图3为ATC扩散算法和CTA扩散算法采用4种不同融合矩阵时网络的瞬时MSD性能曲线。仿真中步长μk=0.01，曲线为100次独立实验得到的平均值。由图可以看出，ATC扩散算法的检测量瞬时误差性能优于CTA扩散算法。两种算法中，采用不同的融合矩阵选取原则，算法的性能不同，可以看出，估计的检测量误差性能优劣顺序为相对自由度准则、平均准则、Metropolis准则、拉普拉斯准则。相对自由度准则依据认知节点相对与相邻节点自由度大小确定矩阵中的元素值，自由度越大的节点拥有更大的融合权重，信息交换速度和融合效果更好。其他3种准则所确定的权值都是依据相邻认知节点中拥有最大自由度的节点确定，这样就会使融合得到的检测量更加接近自由度更大的节点。

(a)ATC扩散

(b)CTA扩散

图3瞬时MSD性能

Fig.3TransientMSDperformance

图4为ATC扩散算法和CTA扩散算法采用4种不同融合矩阵时网络的稳态MSD性能曲线。可以看出:ATC扩散算法的检测量稳态误差性能优于CTA扩散算法;节点2和节点9是两个稳态性能最优的节点，而图2中两个节点的信噪比并不是最高。根据拓扑图可知，节点2有节点7、9两个相邻节点，这两个节点的信噪比较高和自由度较大，因此节点2融合得到的检测量性能更优，估计误差更小。节点9本身的信噪比较高，自由度较大，理应有较好的检测量估计性能。节点3的稳态性能最差，从拓扑结构也可以看出，该节点信噪比较低且自由度较小，唯一的相邻节点6的信噪比以及自由度也不高，因此造成了较大的检测量估计误差。由此可知，认知节点的检测量误差性能是与信噪比和自由度紧密相关的。

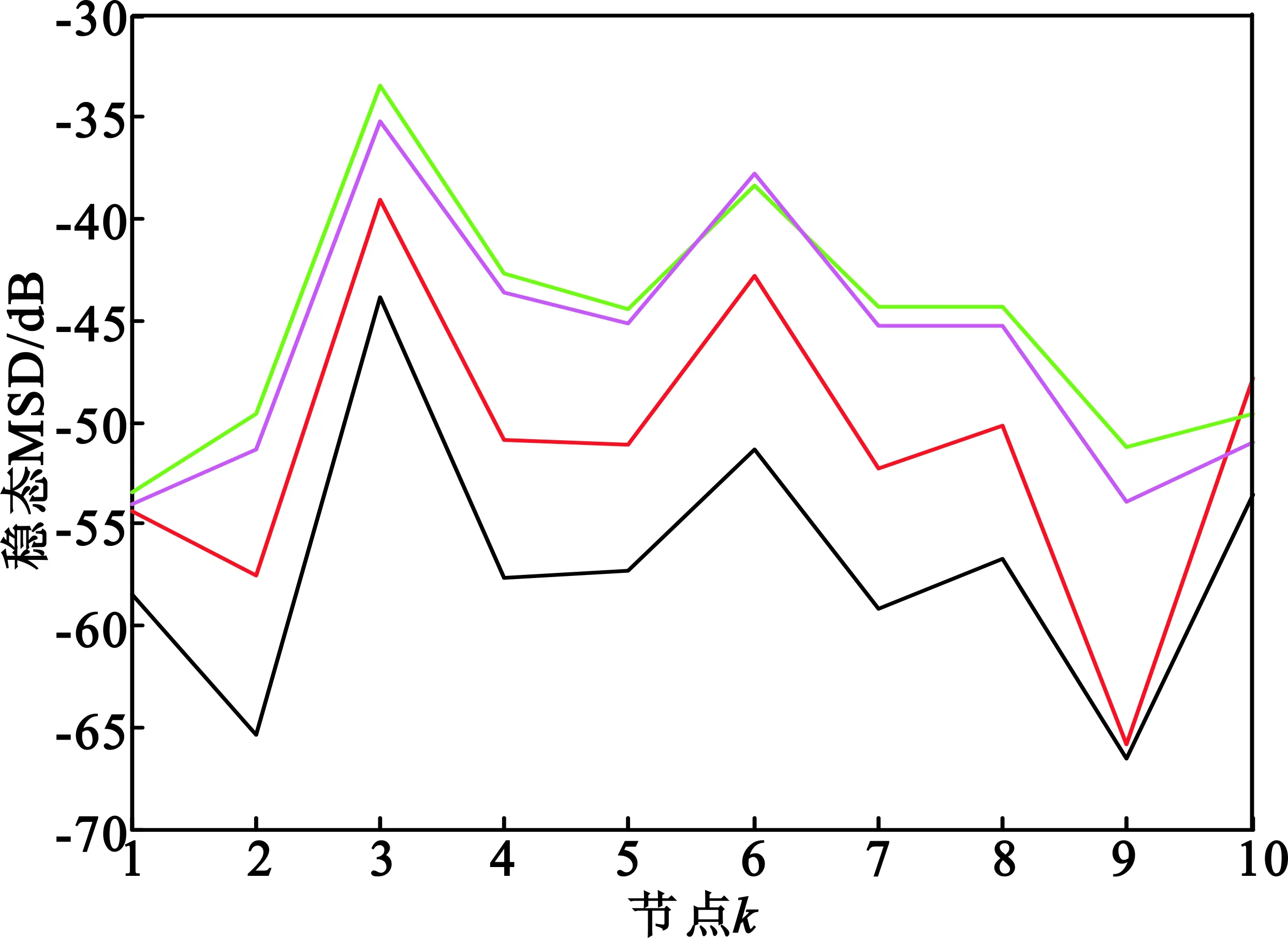
(a)ATC扩散

(b)CTA扩散

图4稳态MSD性能

Fig.4Steady-stateMSDperformance

我们可以得到如下结论：一是采用相同的融合矩阵ATC扩散算法优于CTA扩散算法；二是融合矩阵影响认知节点检测量的自适应过程和融合过程，采用不同融合矩阵选取原则，扩散算法的检测量误差性能不同；三是不同认知节点融合得到的检测量性能与节点所处网络的拓扑结构和信噪比条件有关，节点的信噪比越高、连通性越好，更容易得到好的估计性能。

6　结术语

本文研究了基于扩散策略的分布式CRN协作频谱感知算法的误差性能，给出了自适应扩散策略的协作检测算法，分析了算法的数据处理过程；建立了检测量误差估计模型，推导了检测量估计值的误差公式，并将估计误差的均方偏差性能作为衡量算法性能的标准；采用4种不同融合矩阵的选取原则，对检测量估计误差进行了仿真，验证了融合矩阵参数对协作检测算法的影响。结果表明，可以通过检测量估计误差来衡量参数对检测算法性能的影响。下一步工作中，将利用该方法研究步长等其他参数对算法的影响。

[1]TAKAHASHIN,YAMADAI,SAYEDAH.Diffusionleast-meansquareswithadaptivecombiners[C]//Proceedingsof2009IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing.Taipei:IEEE,2009:2845-2848.

[2]ZENGY,LIANGYC,HOANGAT,etal.Areviewonspectrumsensingforcognitiveradio:challengesandsolutions[J].EURASIPJournalonAdvancesinSignalProcessing,2010(5):1-15

[3]AINOMAEA,TRUMPT,BENGTSSONM.DistributeddiffusionLMSbasedenergydetection[C]//Proceedingsof2014 6thInternationalCongressonUltraModernTelecommunicationsandControlSystemsandWorkshops(ICUMT).St.Petersburg,Russia:IEEE,2014:176-183.

[4]RAZAA,EJAZW,AHMEDSS,etal.Consensus-baseddistributivecooperativespectrumsensingformobileadhoccognitiveradionetworks[J].InternationalJournalofDistributedSensorNetworks,2013(2)：1-10.

[5]ZHANGW,WANGZ,GUOY,etal.Distributedcooperativespectrumsensingbasedonweightedaverageconsensus[C]//Proceedingsof2011IEEEGlobalTelecommunicationsConference(GLOBECOM2011).Houston,Texas,USA：IEEE,2011:1-6.

[6]CATTIVELLIFS,SAYEDAH.DiffusionLMSstrategiesfordistributedestimation[J].IEEETransactionsonSignalProcessing,2010,58(3):1035-1048.

[7]TUSY,SAYEDAH.Diffusionstrategiesoutperformconsensusstrategiesfordistributedestimationoveradaptivenetworks[J].IEEETransactionsonSignalProcessing,2012,60(12):6217-6234.

[8]姚少林,张政保,许鑫,等.基于扩散策略的分布式协作频谱检测[J].电讯技术，2015，55(12)：1401-1406.

YAOShaolin,ZHANGZhengbao,XUXin,etal.Distributedcooperativespectrumdetectionalgorithmbasedondiffusionstrategy[J].TelecommunicationEngineering,2015,55(12):1401-1406.(inChinese)

[9]张政保,姚少林,许鑫,等.基于扩散策略的分布式实时频谱检测算法[J].电子与信息学报，2015，37(12)2858-2865.ZHANGZhengbao,YAOShaolin,XUXin,etal.Real-timedistributedcooperativespectrumdetectionalgorithmbasedondiffusionstrategy[J].JournalofElectronics&InformationTechnology,2015,37(12)：2858-2865.(inChinese)

[10]SAYEDAH.Diffusionadaptionovernetworks[M].Amsterdam,Netherlands:ElsevierAcademicPressLibraryinSignalProcessing,2013.

[11]CATTIVELLIFS,SAYEDAH.Distributeddetectionoveradaptivenetworksusingdiffusionadaptation[J].IEEETransactionsonSignalProcessing,2011,59(5):1917-1932.

[12]AL-SAYEDS,ZOUBIRAM,SAYEDAH.Robustdistributeddetectionoveradaptivediffusionnetworks[C]//Proceedingsof2014IEEEInternationalConferenceonAcousticsSpeechandSignalProcessing(ICASSP).Florence,Italy:IEEE,2014:7233-7237.

[13]BRACAP,MARANOS,MATTAV,etal.Asymptoticperformanceofadaptivedistributeddetectionovernetworks[EB/OL].[2016-01-18].http://arxiv.org/abs/1401.5742. 2014.

[14]TAKAHASHIN,YAMADAI,SAYEDAH.Diffusionleast-meansquareswithadaptivecombiners:formulationandperformanceanalysis[J].IEEETransactionsonSignalProcessing,2010,58(9):4795-4810.

郭超(1991—),男，湖北十堰人，2014年于西安科技大学获学士学位，现为军械工程学院硕士研究生，主要研究方向为认知无线电理论与技术；

GUOChaowasborninShiyan,HubeiProvince,in1991.HereceivedtheB.S.degreefromXi＇anUniversityofScienceandTechnologyin2014.Heisnowagraduatestudent.Hisresearchconcernscognitiveradiotheoryandtechnology.

Email:guochaojunxie@163.com

张政保(1965—)，男，河北石家庄人，2005年于军械工程学院获博士学位，现为军械工程学院教授、硕士生导师，主要研究领域为认知无线电、信息安全技术；

ZHANGZhengbaowasborninShijiazhuang,HebeiProvince,in1965.HereceivedthePh.D.degreefromOrdnanceEngineeringCollegein2005.Heisnowaprofessorandalsotheinstructorofgraduatestudents.Hisresearchconcernscognitiveradiotechnologyandinformationsecuritytechnology.

Email:zhengbaozhang@163.com

姚少林(1992—)，男，河南洛阳人，2015年于军械工程学院获硕士学位，现为助理工程师，主要从事复杂电磁环境综合效应研究；

YAOShaolinwasborninLuoyang,HenanProvince,in1992.HereceivedtheM.S.degreesfromOrdnanceEngineeringCollegein2015.Heisnowanassistantengineer.Hisresearchconcernscomprehensiveeffectsofcomplexelectromagneticenvironment.

Email:yaoshaolin72@gmail.com

刘广凯(1990—)，男，河北石家庄人，2015年于军械工程学院获硕士学位，现为博士研究生，主要研究方向为通信抗干扰技术。

LIUGuangkaiwasborninShijiazhuang,HebeiProvince,in1990.HereceivedtheM.S.degreesfromOrdnanceEngineeringCollegein2015.Heiscurrentlyworkingtowardtheph.D.degree.Hisresearchconcernscommunicationanti-jammingtechnology.

Error Performance Analysis of Adaptive Diffusion Algorithm

GUO Chao1，ZHANG Zhengbao1，YAO Shaolin2，LIU Guangkai1

(1.Department of Information Engineering,Ordnance Engineering College,Shijiazhuang 050003,China；2.State Key Laboratory of Complex Electromagnetic Environment Effects on Electronic and Information System,Luoyang 471003,China)

In order to analyze the influence of the parameters of the fusion matrix and the step size on the adaptive diffusion algorithm in distributed cooperative spectrum sensing cognitive radio networks(CRNs),the error performance of the estimator is studied.The general expression of the adaptive diffusion algorithm is given. The error formula of the measurement is deduced and the transient network mean square deviation(MSD) and steady state MSD of each node are used as the standard to measure the performance of the algorithm. The results show that the different fusion matrix selection rules can influence the detection performance of the diffusion algorithm and the algorithm parameters can be studied by using the error estimation of statistics.

cognitive radio；cooperative spectrum sensing；distributed estimation；diffusion strategy；consensus strategy；error performance analysis

10.3969/j.issn.1001-893x.2016.09.003

2016-02-28；

2016-05-11Received date:2016-02-28；Revised date：2016-05-11

TN911

A

1001-893X(2016)09-0963-06

Email: wuxc@shao.ac.cn

引用格式：郭超，张政保，姚少林，等.自适应扩散算法的误差性能分析[J].电讯技术，2016,56(9):963-968.[GUO Chao，ZHANG Zhengbao，YAO Shaolin,et al.Error performance analysis of adaptive diffusion algorithm[J].Telecommunication Engineering,2016,56(9):963-968.]

**通信作者：guochaojunxie@163.comCorresponding author：guochaojunxie@163.com