中国A股市场动量效应与“动量崩盘”现象研究
2016-10-19曾啸波
■曾啸波
中国A股市场动量效应与“动量崩盘”现象研究
■曾啸波
动量效应作为一种金融异象,广泛存在于各个市场。然而在丰厚收益的背后却存在着巨大的风险,学术界称之为“动量崩盘”。本文在确定中国A股证券市场动量效应的基础上,进一步研究了动量组合的风险性质。结果表明:A股市场存在周度的动量效应;且该周度效应无法被CAPM和Fama-French三因子模型所解释;A股的周度动量效应没有出现普遍存在于其他动量市场的“动量崩盘”现象,表明在A股市场实施动量策略,不仅收益比美国市场更丰厚,而且风险更小;而动量组合在牛熊市中不对称的收益表现,使得动量收益可以和股票期权一样被市场预计波动率所解释。
动量效应;动量崩盘;预计波动率
曾啸波(1984-),硕士研究生,上海杉达学院金融系,讲师。(上海201209)
一、引言
动量效应指的是资产价格按照原有的趋势继续运行的惯性,即过去一段时间表现良好的资产在将来一段时间内仍然表现良好,而过去表现较差的资产在将来一段时间内表现仍然较差。投资者通过购买过去表现良好的资产,同时卖出过去表现差的资产构建动量套利组合,利用动量效应进行获利。
关于动量效应的研究最早开始于Jegadeesh和Titman(1993),他们发现美国股票市场上存在着平均每月1%的动量利润,并且该动量利润无法用传统的金融理论进行解释。但是最近的研究也发现,美国市场上的动量效应存在着“动量崩盘”现象,即动量套利组合在大级别熊市的反弹中,会遭遇非常大的损失。本文的主要工作是考察中国A股市场上的动量效应,除了对动量的存在性和动量利润来源解释进行研究以外,更进一步考察“动量崩盘”现象是否同样也发生在中国市场上。
本文首先利用月度和周度数据检验了中国A股市场的动量存在性,使用与Jegadeesh和Titman(1993)相同的构造法发现在中国市场上不存在月度的动量效应,仅存在1~3周的短期周度动量效应,且在(1,1)①(J,K)策略是指动量效应的考察形成期为J,持有期为K。例如周度(1,1)策略指考察动量效应时,形成期为1周,持有期为1周;月度(6,3)策略指形成期为6个月,持有期为3个月。以此类推。和(2,1)的策略上,动量利润要高于美国市场。
接下来,本文使用CAPM模型和Fama-French三因子模型对周度动量收益进行解释,发现同美国市场的结果一致,两个传统的金融学模型都无法对动量收益作出解释,并且在控制了这些变量后,动量收益不减反增。这样的结果使得对动量效应这一金融异象的风险性质研究变得更重要。
本文第五部分检验了周度动量效应是否存在“动量崩盘”现象。发现当市场在熊市反弹时,动量组合的贝塔值同熊市时没有显著区别;当市场在牛市中反转时,动量组合的贝塔值比牛市中显著减少,相当于给组合提供了“保护”。因此中国A股市场的动量效应,不仅仅在利润上要高于美国市场,在风险上也小于美国市场,并不会出现“动量崩盘”现象。而鉴于动量组合在牛熊市的反转行情中表现出和期权类似的不对称收益形态,本文又使用市场预计波动率来解释动量组合,发现市场预计波动率能较好地解释动量收益,当预计波动率增加时,动量组合的收益将会减少;但在牛市中,当波动率增加时,动量组合的收益将会增加。
本文的创新之处在于:一是首次考察中国A股市场中周度动量效应的“动量崩盘”存在性,发现国内市场在动量效应上相对于国外市场除了收益更高以外,面临的风险更小;二是鉴于动量组合在牛熊市中反转时表现出不同的收益率,这种类同于期权的不对称收益率,可以像期权价格一样,被市场的预计波动率所解释,并且发现随着市场波动率的增加,动量组合收益减少,而当在牛市中波动率增大时,会改善动量组合的收益。
二、文献回顾
(一)动量效应的存在性
股票市场的动量效应最早由Jegadeesh和Titman(1993)发现,他们发现过去3~12个月收益高的股票在接下来3~12个月仍然表现较好,而过去3~12个月收益低的股票在接下来3~12个月仍然表现差,利用这一现象构造的套利组合能够获得持续显著的异常收益,大约为每月1%。此后,Rouwenhorst(1998)研究发现在欧洲十二个国家的股票市场存在与美国类似的动量效应,并且他还发现在其他新兴市场也存在动量效应。除了股票资产外,外汇和大宗商品市场也被发现存在类似的动量效应。
关于中国市场动量效应的存在性研究始于1990年代末期,研究结论并不一致,一部分学者发现在月度数据中存在反转效应;而一部分学者却在特定形成期和持有期或一定条件下发现了月度的动量效应;周度周期上,有较多的学者研究发现了在特定的形成期和持有期,存在着动量效应。比较这些研究,结论的不同主要由于研究区间、时间频率、样本选择、处理数据的方法不同导致。本文在明确以上规则的情况下,将再次验证中国市场的动量效应存在性。
(二)动量效应的解释
对于动量效应的解释,有从传统金融学领域,如Jegadeesh和Titman(1993)用CAPM模型对其进行解释,结果发现动量组合所承担的市场风险不足以解释其高额收益;有从行为金融学对动量效应进行解释,分为反应不足、过度反应以及正反馈交易等;此外,还有从交易成本、知情交易甚至文化差异等其他角度来解释动量效应的。由于市场缺乏统一一致的认定,本文继续使用传统的金融学理论来再次尝试解释国内的动量效应。
(三)“动量崩盘”现象
最早发现“动量崩盘”现象的是Daniel和Moskowitz(2013),他们发现在美国证券市场上,尽管存在着显著的月度动量效应,但在长期熊市后的反弹行情里,动量组合遭遇了巨大的损失,动量组合有着相当大的尾部风险,收益率呈现严重的负偏形态。不仅如此,他们还发现,除了美国股票市场,在其他股票市场包括英国、日本和欧洲大陆地区的股票市场,以及美国国债、大宗商品、外汇等其他资产市场都发现了“动量崩盘”现象。
学术界对“动量崩盘”现象的解释并不一致,Yan(2013)认为是拥挤交易造成的,拥挤交易会造成价格偏离基本面,特别是当卖空机制受限造成套利不便时,更加大了这种偏离,进而促发了这种“崩盘”。而Barroso和Santa-Clara(2015)认为是由动量因子本身的性质决定的,动量的风险是可以预测和控制的,而经过风险控制的动量策略可以使得动量组合的夏普比例提升一倍。
目前尚没有人对国内市场研究过“动量崩盘”现象的存在性,也没有研究过在熊市中反转是否会遭遇收益率的大幅回撤,因此本文在文后尝试研究动量组合在长期或短期趋势行情中反转时的组合性质和特点。
三、动量效应的存在性
(一)研究设定与数据样本
本文根据Jegadeesh和Titman(1993)对于动量效应的研究设计,采用重叠法来衡量中国A股市场的动量效应。由于国内文献分别考察过月度和周度上的动量效应,因此,本文也同时考察月度和周度周期上的动量效应,以便和前人的结果作比较。
动量效应的测度分为形成期(J)和持有期(K),对形成期内每只股票的收益率进行排名,选取表现最好的10%股票作为赢家组合,选取表现最差的10%股票作为输家组合,同时买进赢家组合,卖空输家组合组成套利组合,计算该套利组合在持有期内的收益率。如果组合的收益率显著为正,则说明存在动量效应,如果收益率显著为负,则说明不存在动量效应,而存在反转效应。
数据样本选择所有中国证券市场上交易的A股①包括已经退市的股票。,由于中国证券市场从1996年底开始实施涨跌停板制度,为保证研究数据的质量,因此研究样本的时间区间选择1997年至2014年底,其中月度收益率、周度收益率数据均来自国泰安的CSMAR数据库。
(二)实证结果与分析
基于样本数据,计算月度周期下不同(J,K)策略下的套利组合收益,得到的结果见表1。
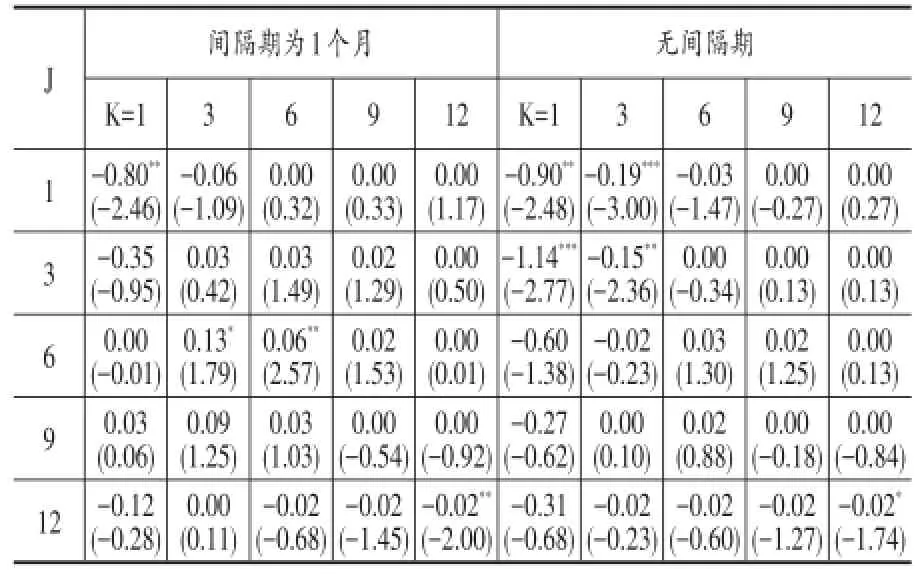
表1 基于月度数据的动量效应
根据表1,我们可以看出无论在形成期与持有期期间是否存在间隔,动量效应都不明显。仅有的显著的动量效应存在于(6,3)和(6,6)策略,但是平均一个月0.13%的动量收益远远低于同期无风险收益率。因此认为中国A股市场不存在国外市场普遍存在的动量效应。
进一步分析发现,A股市场上,在短期的形成期和持有期上,都存在着不同程度的反转效应,特别是无间隔期的(1,1)和(3,1)策略收益,达到了平均每月0.90%和1.14%,远高于同期的无风险收益率。
此外,无间隔期的动量收益普遍低于有间隔期的动量收益,原因可能是大量的动量交易会使得股价在短期内偏离正常范围,造成股价短期的回补,这一点与国外的情况类似,因此在研究动量效应时,通常都间隔一个时间周期以消除这种影响。
基于样本数据,计算周度周期下不同(J,K)策略下的套利组合收益,得到的结果见表2。
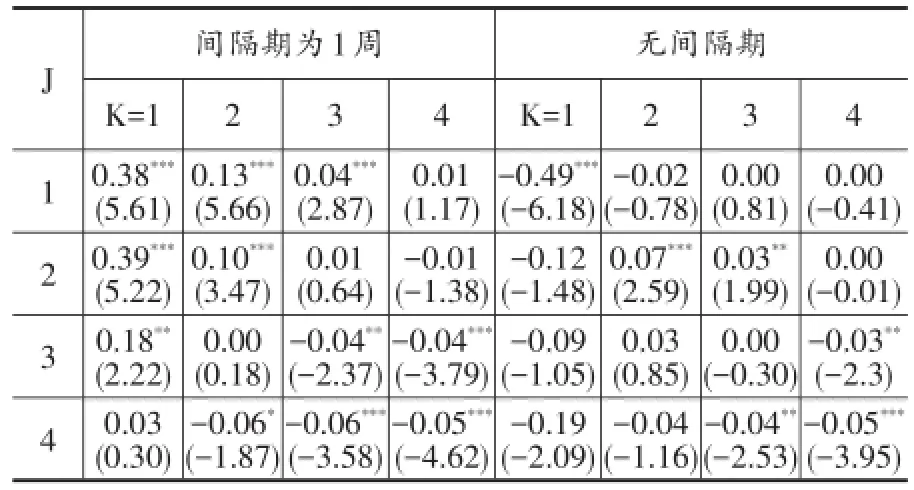
表2 基于周度数据的动量效应
根据表2,我们可以看出,在中国A股市场上,当间隔期为1周且形成期为1周或2周时,存在较为明显的动量效应,特别是(1,1)和(2,1)策略,动量收益达到平均每周0.38%和0.39%,远远高于当时的市场收益和无风险收益,也高于美国平均每月1%的动量收益。
此外还发现,当间隔期为1周时,随着持有期的增加,动量收益逐渐减少,甚至出现了反转效应。表明动量效应随持有期的增加而减少。并且当形成期和持有期为3周或4周时,组合呈现了明显的反转效应,表明动量效应随着形成期的增长而减少,说明国内动量效应普遍存在于较短周期上。而当不考虑间隔期时,套利组合在大多数情况下表现出了反转效应,特别是(1,1)策略,这和月度数据的结论类似,是市场短期内偏离正常价格范围所致。
四、动量效应与CAPM模型和Fama-French三因子模型
(一)研究设定与数据样本
既然表2中显示出了在周度周期上较为明显的动量效应,那么这显著的动量收益到底源自哪里?是市场异象还仅仅是对承担风险的一种补偿?我们利用CAPM和Fama-French的三因子模型,分别尝试去解释周度周期上的动量收益。首先利用套利组合收益对市场风险溢价进行回归:
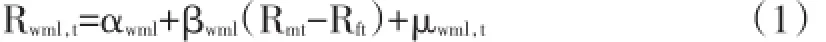
其中,Rwml,t=Rwt-Rlt,Rwt和Rlt分别为赢家组合和输家组合在t月的收益率,Rft为t月的无风险收益率,Rmt为t月的市场回报率。
进一步,控制市值因子与账面市值比因子,使用三因子模型尝试对动量收益进行解释:
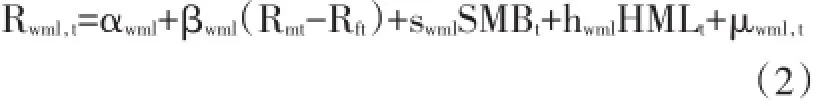
其中,SMBt是市值因子,HMLt是账面市值比因子。
数据仍然选用1997年至2014年年底的数据,只考虑周度套利组合收益率作为因变量,市场回报率选择上证A股指数的周度收益率。周度无风险收益率和周度三因子数据来源为锐思金融研究数据库。
(二)实证结果与分析
对模型(1)和(2)分别做回归,结果见表3。

表3 套利组合收益的CAPM与Fama-French三因子模型实证结果
在表3中可以发现,CAPM模型当控制了市场溢酬风险后,套利组合的收益率α非但没有减少,反而有所增加,例如(1,1)和(2,1)策略,分别增加了每周0.01%的收益率,表明动量效应的收益并非是由于套利组合承担了市场风险所要求的风险补偿。
而在三因子模型回归结果中发现,当进一步控制了市值因子和账面市值比因子后,动量效应的收益较CAPM模型更提高了一些,(1,1)和(2,1)策略分别提高了每周0.02%和0.01%,说明三因子模型也无法解释动量效应。这与刘博和皮天雷(2007),宁欣和王志强(2012)的结论类似。
套利组合的CAPM和Fama-French三因子模型的实证结果说明,从风险补偿的角度解释中国A股市场上存在的周度动量效应不太成功,因此我们观测到的动量效应极有可能是市场中的一种金融异象。而大量机构投资者的“正反馈交易”特性(陈卓思等,2008)也从某种程度上说明了这种异象的存在。因此研究该套利组合本身的风险性质将有助于提高市场中机构投资者的收益率进而提高市场中机构投资者的比例,优化市场参与者结构。
下面我们以周度动量效应显著的(1,1)策略为例,进一步研究该策略下,动量效应的风险问题。
五、“动量崩盘”现象的存在性与特点分析
(一)研究设定与数据样本
国外关于动量风险的研究发现,套利组合在某些情况下会遭受巨大的损失,并且“动量崩盘”现象往往发生在市场巨幅下跌之后的反弹时期,主要原因是,当市场处于熊市时,赢家组合往往包含的是那些低β的股票,而输家组合往往包含的是那些高β的股票,因此一旦反弹,赢家组合的收益会大幅度小于输家组合,使套利组合遭受损失。
为检验中国A股市场是否同样存在“动量崩盘”现象,参考Daniel和Moskowitz(2013)的模型,考虑如下三个回归:
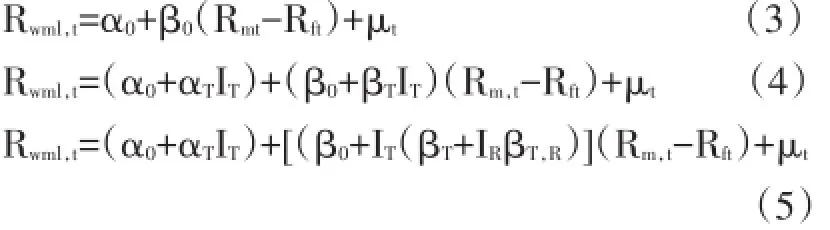
其中,Rwml,t,Rm,t和Rft定义同第四部分,IT和IR是虚拟变量,当市场经历了趋势行情,IT取值为1,否则取值为0。当市场在当前周期出现趋势反转时,则IR取值为1,否则取值为0。由于原始数据取自1997年至2014年,而在定义趋势时,需要用到50周的数据,因此第五部分回归的样本区间为1998年至2014年的周度数据。模型(3)是CAPM模型,记作回归1,作为基准。
模型(4)考察在牛熊市时以及趋势和波动市时套利组合的表现差异,参考Daniel and Moskowitz(2013)对于熊市的定义,选取长期的市场收益率作为参考,如果过去50周市场累积收益率为负,记IT= 1,记作回归2。考虑到中国A股市场趋势行情较少,波动行情较多,振幅较大,因此选取更短周期的市场收益率作为参考,并且不区分牛熊市,当过去市场8周的累积收益率低于-10%或者高于+10%时,IT=1,记作回归3。
模型(5)考察在市场反转时套利组合的情况。如果过去50周市场累积收益率为负/正,且当周的市场收益率为正/负,则IT=1,IR=1记作回归4/回归5。回归4和回归5试图发现当市场反转时,组合的β值的特征。进一步,考察市场短期趋势反转时组合的情况。如果过去8周市场累积收益率为-10%/+ 10%,且当周的市场收益率为正/负,则IT=1,IR=1。分别记作回归6和回归7。
(二)实证结果与分析
首先给出各10%组合的描述性统计量,见表4。
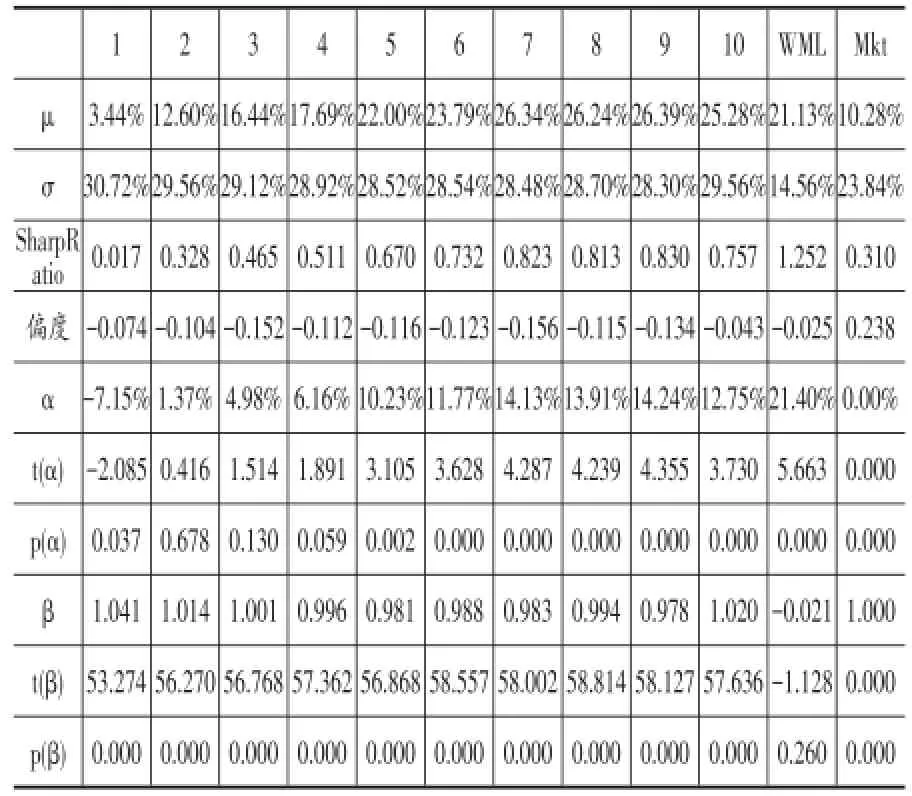
表4 各10%组合及套利组合和市场的描述性统计量
从表4可以看出,形成期收益越高的组合持有期收益一般也越高,说明动量效应明显,同时各个组合的波动率较为接近,因此形成期收益较高的组合往往夏普比率也越高。每个10%组合的偏度都为负,说明各个组合都面临着一定的尾部风险,同时套利组合表现出最高的夏普比例,且负偏程度优于所有10%组合。从描述性统计的结果来看,套利组合似乎不存在“动量崩盘”现象,且比各10%组合更稳健。
考察“动量崩盘”现象的回归结果见表5。
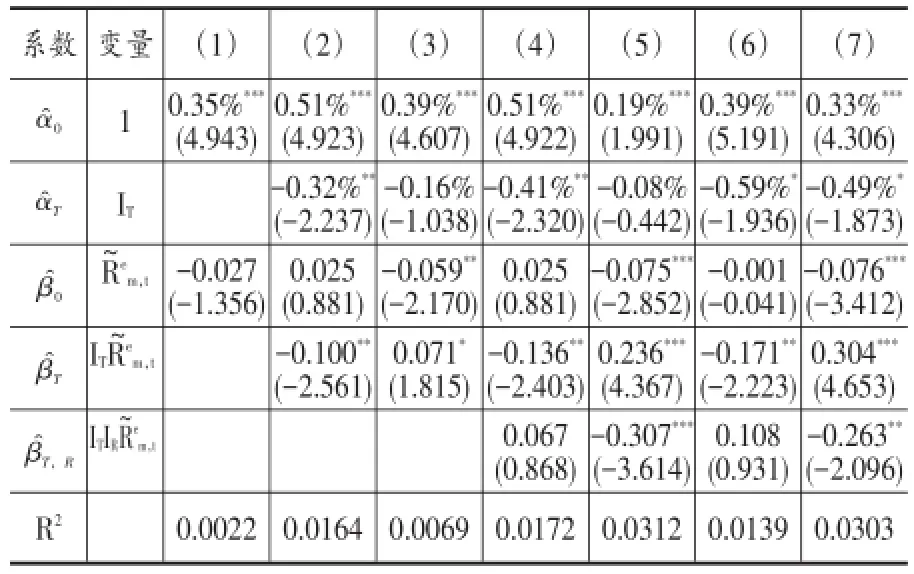
表5 “动量崩盘”现象实证结果
从表5可以看出,尽管使用了1998年至2014年的数据,回归1的结果和表3的(1,1)的CAPM模型的实证结果非常接近,这从一定程度上证明了(1,1)策略动量效应的鲁棒性。回归2的α^T显著,说明动量效应在牛熊市之间表现不同,在长期牛市中,动量收益达到了每周0.51%,而在熊市中,动量收益每周只有0.19%,这表明动量效应在牛熊市之间表现不同,且在牛市中动量效应更明显。这与贺学会和陈诤(2006)的结果类似。同时,回归2的β^T显著为负,表明在熊市中,套利组合的β值为负,而在牛市中β值为正,这和直观感受也是一样的,当市场下跌时,负β的组合得到正收益,而当市场上升时,正β的组合得到正收益。回归3的α^T不显著,表明如果市场存在短期趋势无论上升还是下降,动量效应在这些趋势中没有区别。
回归4的β^T,R不显著,表明在长期熊市下,反弹当周套利组合的β并没有和之前下降趋势时的β有明显的差异,这一点和Daniel和Moskowitz(2013)对于美国股市的发现不同。回归5的β^T,R显著为负,表明当市场在长期牛市中反转下跌时,套利组合的负β值使得套利组合在市场下跌时能增加收益,表明中国A股市场的动量效应,非但没有国外股市在熊市反转时的“动量崩盘”现象出现,甚至出现了在牛市反转下跌时的“保护”。回归6和7旨在考察套利组合在更短周期上的表现,结果回归6的β^T,R不显著,而回归7的β^T,R显著为负,同长周期的表现一致。
(三)动量套利组合收益与市场波动
动量组合在熊市中反弹时的表现和在熊市中的表现无异,而同时,在牛市中下跌时的表现却给组合提供了“保护”。动量组合在牛熊市中反转时显示出的收益不对称性,和股票期权的收益类似。因此,类同于用市场波动率来预测期权价格,此处考虑使用市场波动率来对动量套利组合进行预测。利用每日市场收益率计算每周市场波动率,然后利用该周波动率作为下周的波动率的估计值,对动量套利组合进行预测。
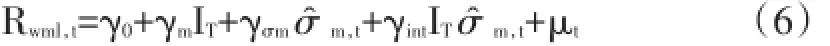
其中,IT的定义同表5的回归(5),σ^m,t=σm,t-1。实证结果见表6。
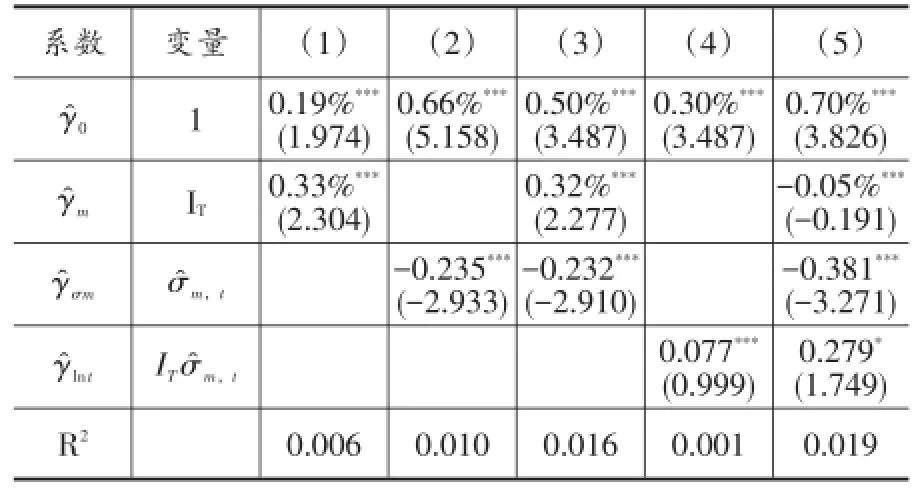
表6 动量收益与市场波动率
表6的回归(1)表明,牛市中套利组合的收益要显著高于熊市中套利组合,这和表5回归(1)的结论一致。回归(2)显示,当市场的预计波动增大时,会减少套利组合的收益。回归(3)的系数和回归(1)与回归(2)非常接近,表明牛熊市与市场波动率这两个因素,都能各自独立的预测动量套利组合。回归(4)的γ^lnt显著为正,说明在牛市中预计波动率越大,动量套利组合的收益越高。回归(5)的各项系数均显著,表明在牛市中动量收益要显著高于熊市收益,且市场预计波动率的提升会显著降低动量组合的收益率,但如果是在牛市中,则波动率的提高会增加动量套利组合的收益率,说明在中国A股市场上,动量套利组合在牛市中的波动中,有较强的“保护”作用,这与美国证券市场上的“动量崩盘”现象有很大的区别。
(四)稳健性检验
使用同样具有显著周度动量效应的(2,1)策略收益作模型(3)~(6),所得各项系数的符号与显著性都与(1,1)策略的结果类似,故认为以上结论对周度动量效应是稳健的。
六、结论
综上,本文的主要结论如下:
1.我国A股市场上不存在月度动量效应,但存在周度动量效应,特别是当间隔期为1周时,(1,1)、(1,2)、(2,1)、(2,2)与(3,1)策略表现出远超无风险利率的收益。
2.无论是CAPM模型还是Fama-French的三因子模型都无法解释中国A股市场上的周度动量效应,可以认为A股市场上的动量效应是一种无法用传统金融学解释的“金融异象”。
3.A股市场中牛市中的动量效应要大于熊市时。此外同美国股市及全球多项资产的动量组合具有“动量崩盘”的特点不同,A股市场的动量效应非常稳健,即在熊市中的反弹并没有使得动量组合的回报率降低,同时在牛市中的回调甚至还使得动量组合的回报率提升。表明在中国A股市场实施动量策略,能获得比在美国实施同样策略更为稳健的收益回报率。
4.由于动量组合在牛熊市中反转所表现出的收益不对称性和股票期权类似。因此动量组合的收益和期权类似,可以很好的被市场的预计波动率所解释,当市场波动率增大时,会显著地降低组合收益率。与此同时,牛市中的波动率增加会改善动量组合的回报率。
本文的研究结果有助于股票市场的参与者,特别是使用动量策略的投资者进一步了解中国股市的规律,在中国市场中使用动量策略的投资者应该比在国外同类市场中的投资者更有信心。
[1]Daniel K D,Moskowitz T J 2013.Momentum crashes.Swiss Finance Institute Research Paper[J].14~16.
[2]陈卓思,高峰,祁斌.机构投资者交易行为特征研究[J].金融研究,2008,(4):122~130.
[3]贺学会,陈诤.基于牛市和熊市不同周期的股票市场动量效应研究[J].财经理论与实践,2006,(27):40~44.
[4]宁欣,王志强.基于残差收益的动量或反转效应:来自中国A股市场的经验证据[J].投资研究,2012,(12):123~136.
F830.91
A
1006-169X(2016)09-0076-06
本文受上海市教育委员会和上海市教育发展基金会“晨光计划”(14CGB04),上海杉达学院校基金(2015hx03)资助。
