Thermal and tilt effects on bearing characteristics of hydrostatic oil pad in rotary table*
2016-10-18ZhifengLIU刘志峰ChengpengZHAN湛承鹏QiangCHENG程强
Zhi-feng LIU (刘志峰), Cheng-peng ZHAN (湛承鹏), Qiang CHENG (程强),2,
Yong-sheng ZHAO (赵永胜)1, Xiao-yan LI (李小燕)1, Yi-da WANG (王义达)1
1. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology,Beijing 100124, China, E-mail:lzf@bjut.edu.cn
2. State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China
Thermal and tilt effects on bearing characteristics of hydrostatic oil pad in rotary table*
Zhi-feng LIU (刘志峰)1, Cheng-peng ZHAN (湛承鹏)1, Qiang CHENG (程强)1,2,
Yong-sheng ZHAO (赵永胜)1, Xiao-yan LI (李小燕)1, Yi-da WANG (王义达)1
1. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology,Beijing 100124, China, E-mail:lzf@bjut.edu.cn
2. State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China
Hydrostatic pads are key components of a constant flow compensation hydrostatic rotary table. The tilt and thermal effects due to the partial load, the manufacturing errors and the friction must be considered. However, designers are more likely inclined to ignore these effects. In this work, the coupled characteristics of the tilt and thermal effects are studied. A coupled mathematical model to calculate the bearing properties of the pads is built. This model takes into consideration of tilt and thermal effects and is used to solve the flow problem by the finite difference method. The characteristics of the oil pad, including, the recess pressures, the load carrying capacity and the damping coefficients, are obtained and the tilt and thermal effects are analyzed. It is observed that the tilt has a tremendous impact on the bearing characteristics of the hydrostatic pad. The recess pressure, the load carrying capacity and the stiffness are reduced by 50% and the pressure distribution and the temperature distribution of the oil film also change significantly. When the pads work under a tilt operation, a larger land width is better for its bearing properties. It is also observed that the thermal effect is significant and cannot be ignored.
thermo-hydrodynamic lubricant, tilting, Reynolds equations, constant flow compensation
Introduction
Hydrostatic bearings are widely used in heavy machinery due to their advantageous characteristics of low viscous friction, high load-carrying capacity and high stiffness. Extensive and in-depth research has been carried out for the hydrostatic bearing technology,due to its widespread use and important role in the industry such as machine tools, telescopes, hydropower, and aircraft engines. The basic theory of the hydrostatic lubrication and the basic design of hydrostatic bearing systems can be found in Refs.[1-4]. These methods and theories are widely adopted by designers. However, some special factors should be considered, under various application conditions and manufacturing conditions.
Static and dynamic characteristics are the key properties of hydrostatic bearing systems and were widely studied. Zuo et al.[5]proposed a static loading experiment to determine the static and dynamic characteristics of conical hydrostatic bearings with different compensations. Guo et al.[6]used the finite element method to solve the flow of the fluid film in the conical bearing governed by the Reynolds equation. Using the pressure boundary condition, the bearing stiffness and the damping coefficients were calculated. The numerical results were compared with the experimental results. Gao et al.[7]analyzed the static and dynamic characteristics of hydrostatic guides with rectangle pockets and a PM flow controller.
As we all know, all mechanical parts have manufacturing errors, these errors can be divide in two parts: one is the surface roughness and the other is the geometric error. They both has some impact on the performance of the hydrostatic lubrication. Refs.[8-10] investigated the influence of the surface roughness on various performance characteristics of the hydrostatic thrust bearing based on Christensen roughness model. The roughness was found to have an important influence on the characteristics of the film. When the film thickness and roughness values have the same order of magnitude, the effects of the surface roughness cannot be ignored. Sharma et al.[11], theoretically investigated the influence of the dimple geometry on the fully textured hybrid thrust pad bearing operating with a non-Newtonian lubricant. The result is useful to optimize the sizes of the dimple diameter and depth for the bearing performance. Ramesh et al.[12]used experimental and numerical methods to study the friction characteristics of micro-textured surfaces. Their results indicate that the friction in the case of textured surfaces is 80% lower than that in the case of un-textured surfaces. In this work , the surface roughness effects can be ignored, since the surface roughness of the pad and the guide rail is lower than the thickness of the oil film (ra<8µ m, where the initial film thickness is 100 µm for 9.5 m hydrostatic rotary table).
The geometric error to some extent is equivalent to tilting due to its larger wavelength. The tilt effect was extensively studied. Liu et al.[13]developed a three-dimensional theoretical model to study the effect of disturbances on the dynamic performance of a wavy-tilt-dam (WTD) mechanical seal. Yadav et al.[14],numerically analyzed the influence of the tilt and the different recess shape on the static and dynamic performance characteristics of the hydrostatic thrust pad bearing system. The numerically simulated results indicate that the tilt significantly affects the dynamic and static characteristic parameters. De Pellegrin et al.[15]presented an isoviscous, isothermal model to investigate the influence of hydrostatic recesses on a spring-supported tilting pad thrust bearing. These studies mainly focused on the hydrostatic bearing with a constant supply pressure, which were not coupled with thermal effects.
The thermal effects also attracted many studies. Aksoy and Aksit[16]established a coupled thermoelastohydrodynamics model to predict 3-D thermal,structural and hydrodynamic performance of foil bearings. Dobrica and Fillon[17]proposed a complete thermo-hydrodynamic (THD) steady state model and applied the model to the slider pocket bearing. The constructed model was solved using the finite volume method. The pressure distribution and the velocity fields in the fluid, as well as the temperature distribution across the fluid and solid pad were obtained using this method. Laraqi et al.[18]proposed a 2-D analytical solution to determine the temperature distribution of a thin fluid film confined between two parallel planes on a relative motion. Deresse and Sinha[19]analyzed the thermal and roughness effects on the characteristics of finite rough tilted pad slider bearings. The modified equations for Reynolds number, momentum, continuity and energy were coupled and solved using the finite difference method. Wang and Lu[20]investigated the effect of viscosity on cavitation characteristics of a high speed sleeve bearing.
On the whole, the studies of the tilt effect left many problems unsolved. In fact, it is often difficult to maintain a parallel state between the guide and the supporting oil pad of the turntable due to the manufacturing error, the partial load and the local deformation. Thus, it is necessary for studies to focus on the impact of tilting. In this work, simplified equations of motion, continuity and energy are developed and solved using the finite difference method. Then, the pressure distribution and the temperature distribution of the hydrostatic oil film are obtained. In addition,the recess pressure, the load carrying capacity, the stiffness coefficients and the damping coefficients at different tilting angles are analyzed.
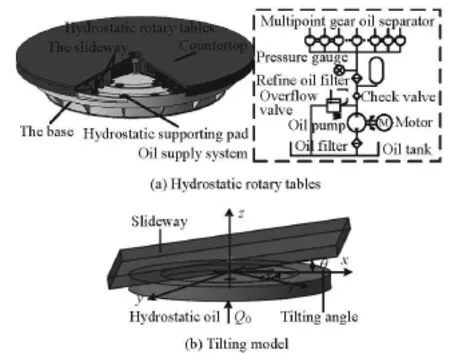
Fig.1 The schematic diagram of tilting model between guide and hydrostatic pad
1. Mathematic model
Hydrostatic rotary tables are widely used in heavy machine tools due to its excellent performance. The schematic diagram of a typical hydrostatic rotary table is shown in Fig.1(a). It mainly consists of the base, the countertop, the supporting system, and the driving system. The supporting system includes supporting oil pads, preloaded oil pads, the radial bearing and the oil supply system. The supporting oil pad is a circular step pad and the rotary table has many supporting pads. They are arranged under the countertop. The preloaded oil pad is the annular step recess pad and provides a pre-pressure to enhance the stiffness of the turntable. The radial bearing is mounted on the center of the turntable. These pads contain a constant flow oil, and in every pad the flow rate is almost the same and there is little interaction between the oil pads bythe use of the multi point gear oil separator. Because all gear pumps of the same shape are connected by one shaft, which forces them to rotate at the same speed and produce the same flow rate.
The hydrostatic supporting pad is a key component of the supporting system and usually is designed for the parallel operation. However, this is not always the case in engineering applications. There always exists a tilt state. Fig.1(b) illustrates the tilting mode between the guide and the hydrostatic pad. The flow rate for the pad is Q0.r,ϕ,zare the polar coordinates andθis the tilting angle.
1.1 Reynolds equation
In this study, it is assumed that thin film lubrication theory is applicable and the flow in the bearing is laminar. Also, the density and the viscosity are assumed to be temperature dependent. Thus, the continuity and Navier-Stokes equations can be simplified as:

where, Eq.(1) is the continuity equation, Eqs.(2)-(4)are the motion equations inr direction,ϕdirection andzdirection, respectively. Integrating both sides of Eq.(3) with boundary conditions:z =0,uϕ=0 and z=hT,uϕ=0at the surface of the pad, the circumferential velocity can be written as

Similarly, integrating both sides of Eq.(2) with boundary conditions:z =0,ur=0and z=hT,ur=0, the radial velocity can be written as

Substituting velocities urand uϕin the continuity equation Eq.(1) and integrating it along the film thickness, the Reynolds equation can be written as
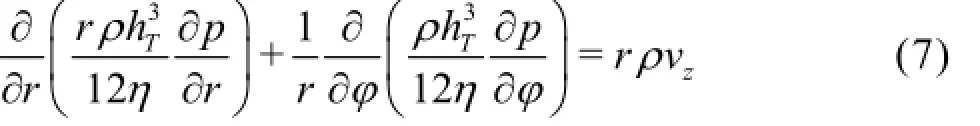
1.2 Energy equations
According to Refs.[15-19], the simplified energy equations can be written as follows

in which no great temperature change is assumed as well as that of the coefficientk , the fluid is considered to be incompressible and under steady-state conditions. The viscosity ηand the densityρ are related to the temperature with the following relationships:

where η0,ρ0and T0are the initial viscosity, density and temperature of the oil film, respectively.

Fig.2 The supporting oil pad
1.3 Hydrostatic supporting oil pad
The typical configuration of a circular step recess oil pad is illustrated in Fig.2.R1,R2are inner and outer radii of the pad,hsis the thickness of the lubricant film under no tilt conditions when the lubricant oil is supplied by a constant flow pump. For a slideway tilt, the tilting angle isθ, the film thickness distribution can be described as

To non-dimensionalize the governing equations,the following non-dimensional variables are defined.


where h0is the initial film thickness,p0is the recess pressure,vzis the squeezed-film velocity at the surface of the slideway,ρaand ηaare the mean density and the mean viscosity,θ0is the maximum tilting angle of the rotary table and θ0=h0/R2. Substituting these parameters into Eqs.(5)-(11), the dimensionless film thickness distribution equation, the Reynolds equation, the energy equation and so on can be rewritten as follows:

where, the dimensionless velocity is:

The fluid boundary conditions for the Reynolds equation and the energy equations are:


The flow rate out of the recess through bearing clearances can be obtained from the governing equation, which is given by

So the recess pressure can be expressed as

Also the load carrying capacity, the stiffness and the damping coefficients are expressed as:


Fig.3 solution scheme
2. Numerical calculation procedures
The system of equations is discretized and solved using the finite difference representations. The results are obtained to an accuracy of ζ<10-6,

whereAccording to Ref.[19], this accuracy is enough for the purpose of this work. Figure 3 shows the overall solution scheme used in the study, and the computation contains the following steps: Step 1: Initialize the input initial parameters and boundary conditions. Step 2: Calculate the film distributionusingandthrough Eq.(13). Step 3: Calculate the velocitiesand the recess pressure p0usingand Eq.(17). Step 4: Calculate the temperature distributionusing Eq. (14). Step 5: Calculate the new density and viscosityandusing Eqs.(15) and (16). Step 6: Calculate the average temperature, the average densityand the average viscosityStep 7: Test for convergence. Step 8: Repeat steps 2-7 till convergence is reached for all field variables. Step 9: Calculate the load carrying capacitywf, the stiffness Kzand the damping coefficients Czby Eqs.(20),(21) and (22).

Table 1 Initial parameters
3. Application and verification
The initial parameters are chosen in accordance with one hydrostatic rotary table and are listed in Table 1. The simulations are carried out according to the algorithm discussed in Section 2. Various bearing characteristics are calculated and analyzed. To ensure the grid independence of the results, the numerical simulations are carried out with different grid systems of nr×nϕ×nz, consisting of 80×80×80, 60×60×60,40×40×40 and 20×20×20 grid points. The load carrying capacities under different tilting angles are obtained with different grids. They are compared and presented in Fig.4. Little difference is found even at the maximum tilt angle and at last, the 60×60×60 grids system is chosen to have a real and effective solution.

Fig.4 Load carrying capacities with different grids systems
In this simulation, various bearing performances of hydrostatic circular step pads are calculated with consideration of the tilt and thermal effects. The bearing characteristics varying with the tilt angle will be analyzed. Finally, various parameters including the recess pressure, the load carrying capacity, the stiffness and the damping are compared to show the necessity of considering the thermal effects. In order to better analyze the results, some parameters like the load carrying capacity, the recess pressure, the temperature, the stiffness and the damping coefficients are normalized by division these parameters with those with no tilt angle or other parameters.


Fig.5 The recess pressure against tilt

Fig.6 Load carrying capacity against tilt
3.1 Bearing characteristics
Figure 5 and Fig.6 show the variations of the normalized recess pressure and the load carrying capacity agaisnt the tilt. It is found thatand wf∗decrease significantly with the increase of the tilting angle, almost by 50% and 48% atrespectively. It is also obvious that the influence of tilting onandwf∗is smaller at a smaller value of the inner radius, and the maximum reductions of the recess pressure and the load carrying capacity are even less than 20% and 6%respectively.
Figure 7 shows the variation of the normalized effective area of the pad against the tilting angle at different inner radii. According to Refs.[1-3], the effective area is calculated by the equation:The figure shows that a higher value of the tilting angle and a smaller value of the inner radius yield a higher value of the effective area. It is also shown that the tilt does not have a great impact on, as compared toandwf∗, the maximum increase is only 18% atand 2% at. Because of the compensation effect of the effective area, the total reduction of the load carrying capacity is smaller than the recess pressure.
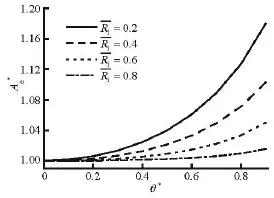
Fig.7 The variation of effective area

Fig.8 The variation of stiffness coefficients against tilt parameters

Fig.9 The variation of damping coefficients against tilt parameters
Figure 8 and Fig.9 show the variation of the stiffness and the damping coefficients against the parameter θ*at different inner radii. It is observed thatanddecrease with the increase of the tilting angle and the maximum reductions are 48% and 47% atθ∗=0.9, respectively. However, the reduction of the inner radius can reduce the reductions ofandwhen the pad is in operation with a tilt angle.
The variations of the average film temperatures against the tilt parameter at different inner radii are presented in Fig.10. It is found that the average temperatures decrease with the increase of the tilting angle. However, the total reduction is not great and the maximum decrease is only 0.7% atIt is also found that the variations of the mean film temperature see small changes at different inner radii and a smaller inner radius value will yield a higher mean film temperature value.

Fig.10 Average temperature vs. tilt parameter

Fig.11 Variations of bearing performance against inner radius

Fig.12 Pressure distribution at different locations of the pads while

Fig.13 2-D pressure contours at various tilting angles
The variations of the normalized bearing performance against the inner radius are shown in Fig.11. It is discovered that all bearing properties decrease with the increase of the inner radius in different curves.The recess pressure vs. the tilt is most sensitive to the inner radius (even a reduction of 90% at the maximum inner radius) and the mean film temperature vs. the tilt is most insensitive to the inner radius (only a reduction of 3.5% at the maximum inner radius). The variations ofare similar, the value ofis slightly larger thanand the value ofis slightly larger than wf#for the same inner radius. The maximum reductions of them are 64%, 60% and 57%, respectively.
From the above analyses, it is seen that the recess pressure is more sensitive to the tilt for constant flow compensation pads and the decrease of the recess pressure is the predominant reason for the decrease of other bearing properties. To some extent, the increase of the effective area against the tilting angle may compensate some reductions of the bearing properties. However, the compensation effect is small and limited. The inner radius has a great influence on the bearing properties of the oil pad and the reduction of the inner radius is good for the anti-tilt ability of the hydrostatic oil pad.
3.2 Pressure and temperatures distributions
The pressure profiles along the various circumferential positions are shown in Fig.12. 2-D pressure contours at various tilting angles are shown in Fig.13. This hydrostatic pad is tilted inx direction. It is observed that the fluid film pressure profiles change significantly with the tilt parameter, with one side increasing more than the other side. As shown in Fig.12, the pressure decreases slightly at ϕ=0 rad, increases greatly atϕ=πrad and almost has no change at)rad. It can also be observed that the increase of the fluid film pressure is greater than the decrease when the pad is in operation with a tilt. As a result,the load carrying capacity of the fluid film will increase with the increase of the tilting angle, if the recess pressure keeps constant (as shown in Fig.7).

Fig.14 Temperature distributions at different locations of the padswhile
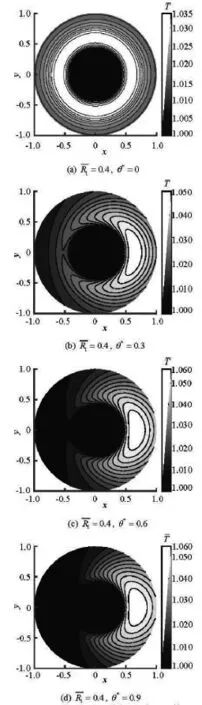
Fig.15 Temperature contours with various tilt parameters


Fig.16 The influence rate of the thermal effects on the performance of hydrostatic pad

Fig.17 Picture of the test site
3.3 Thermal effects
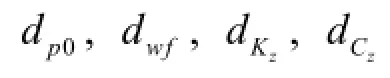
4. Experimental verification
Figure 17 shows the experimental setup of a hydrostatic rotary table developed to verify the proposed model. Here the radius of the table is 0.4 m, and there are eight circular step supporting pads, where the hydrostatic oil in them are all supplied by a constant flow pump. The flatness of the countertop is less than 4 µm, so its effect can be neglected. A force loader is mounted on the holder and it can move along the rail to change the offset of the external loads. The external load is measured by a force sensor and displayed on a digital display. Four eddy current sensors are installed around the table and an LMS Data Acquisition System is used to measure the film thickness of the supporting pads. Other parameters are listed in Table 2.

Table 2 Parameters of the experimental rotary table

Fig.18 Stiffness of rotary table (Ncsis sensor number,hcsis film thickness)
When the partial load is applied on the rotary table, all supporting pads are under a tilt state. While the partial load is 17.56 KN and the offset distance is 0.354 m, the obtained simulation values and the experimental values are shown in Fig.18. The experimentalresults agree well with the model predictions when the tilt is considered. The film thickness in four pads of the table is less than the simulation result when the tilt is not considered, so the proposed model can calculate the characteristics of the supporting pad in rotary tables. It also can be seen that the tilt has a significant impact on the bearing performance of the pad, which cannot be ignored in the design process especially for the heavy-duty hydrostatic rotary table.
5. Conclusions
In the present work, the dynamic and static performance characteristics of hydrostatic oil pads under tilt and thermal effects are studied. The coupled Reynolds equation and energy equation with tilt are solved by the finite difference method. Results can be summarized as follows:
(1) The dynamic and static performances of circular step hydrostatic oil pads change significantly due to the tilt and thermal effects.
(2) The recess pressure, the load carrying capacity, the stiffness coefficients and the damping coefficients decrease remarkably with the tilt and the maximum decrease is as high as 50%. However, the reduction of the inner radius is good for the anti-tilt ability enhancement of the hydrostatic oil pad.
(3) The pressure distribution and the temperature distribution also have a tremendous impact. The film pressure has a large increase in the rise parts of the guide rail and a small decrease in the fall parts of the guide rail, while the film temperature has a large increase in the rise parts of the guide rail and only a small rise in the fall parts of the guide rail.
(4) There is an obvious difference of the bearing performance, when the thermal effect is considered or not. The influence rate for the recess pressure and the load carrying capacity is between 2% and 3%, for the stiffness it is between 6.5% and 10.2%, and for the damping coefficients it is between 4.4% and 9.7%.
(5) Experiment of a hydrostatic rotary table is designed to verify the present model. The experimental result demonstrates that the tilt has an obvious influence on the bearing properties of hydrostatic pads. So to accurately calculate the bearing performance of hydrostatic pads, it is essential to consider the tilt and thermal effects.
Despite these progresses, it is important to note that there is limitations in the method used, which should be further studied in order to have a better understanding of the effects. In this work the deformation of the guide rail is not considered, and this deformation may play some role in the process. Therefore,integrating the hydro-thermodynamics characteristics into the optimization process of hydrostatic pads is another focus for future research.
Acknowledgments
This work was supported by the Jing-Hua Talents Project of Beijing University of Technology, Beijing Nova Program, Basic Research Foundation of Beijing University of Technology, Open Project of State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology.
References
[1] HAMROCK B. J., SCHMID S. R. and JACOBSON B. O. Fundamentals of fluid film lubrication[M]. Boca Raton,USA: CRC Press, 2004.
[2] SZERI A. Z. Fluid film lubrication: Theory and design[M]. New York, USA: Cambridge University Press,2005.
[3] GWIDON W. Stachowiak and Andrew W. Batchelor. Engineering tribology[M]. Fourth Edition, Amsterdam,The Netherlands: Elsevier, 2014.
[4] BART J. C. J.,GUCCIARDI E. and CAVALLAROS. Biolubricants science and technology[M]. London, UK: Woodhead Publishing Ltd, 2013
[5] ZUO X., WANG J. and YIN Z. et al. Comparative performance analysis of conical hydrostatic bearings compensated by variable slot and fixed slot[J]. Tribology International, 2013, 66: 83-92.
[6] GUO H., LAI X. and CEN S. Theoretical and experimental study on dynamic coefficients and stability for a hydrostatic/hydrodynamic conical bearing[J]. Tribology,2009, 131(4): 1701-1707.
[7] GAO Dian-rong, ZHENG Dan and ZHANG Zuo-chao. Theoretical analysis and numerical simulation of the static and dynamic characteristics of hydrostatic guides based on progressive Mengen flow controller[J]. Chinese Journal of Mechanical Engineering, 2010, 23(6): 709-716.
[8] SCHULTHEISS F., HÄGGLUND S. and BUSHLYA V. et al. Influence of the minimum chip thickness on the obtained surface roughness during turning operations[J]. Procedia CIRP, 2014, 13: 67-71.
[9] LIN J. R., HUNG T. C. and CHOU T. L. et al. Effects of surface roughness and non-Newtonian micropolar fluids on dynamic characteristics of wide plane slider bearings[J]. Tribology International, 2013, 66: 150-156.
[10] NADUVINAMANI N. B., HANUMAGOWDA B. N. and FATHIMA B. N. Combined effects of MHD and surface roughness on couple-stress squeeze film lubrication between porous circular stepped plates[J]. Tribology International, 2012, 56: 19-29.
[11] SHARMA S. C., YADAV S. K. Performance analysis of a fully textured hybrid circular thrust pad bearing system operating with non-Newtonian lubricant[J]. Tribology International, 2014, 77: 50-64.
[12] RAMESH A., AKRAM W. and MISHRA S. P. et al. Friction characteristics of microtextured surfaces under mixed and hydrodynamic lubrication[J]. Tribology International, 2013, 57: 170-176.
[13] LIU W., LIU Y. and HUANG W. et al. Effect of disturbances on the dynamic performance of a wavy-tilt-dam mechanical seal[J]. Tribology International, 2013, 64: 63-68.
[14] YADAV S. K., SHARMA S. C. Performance of hydrostatic tilted thrust pad bearings of various recess shapesoperating with non-Newtonian lubricant[J]. Finite Elements in Analysis and Design, 2014, 87: 43-55.
[15] De PELLEGRIN D. V., HARGREAVES D. J. An isoviscous, isothermal model investigating the influence of hydrostatic recesses on a spring-supported tilting pad thrust bearing[J]. Tribology International, 2012, 51: 25-35.
[16] AKSOY S., AKSIT M. F. A fully coupled 3D thermoelastohydrodynamics model for a bump-type compliant foil journal bearing[J]. Tribology International, 2015, 82: 110-122.
[17] DOBRICA M. B., FILLON M. Thermohydrodynamic behavior of a slider pocket bearing[J]. Journal of Tribology,2006, 128(2): 312-318.
[18] LARAQI N., RASHIDI M. M. and GARCIA De MARIA J. M. et al. Analytical model for the thermo-hydrodynamic behaviour of a thin lubricant film[J]. Tribology International, 2011, 44(9): 1083-1086.
[19] DERESSE G. A., SINHA P. THD analysis for finite slider bearing with roughness: Special reference to load generation in parallel sliders[J]. Actamechanica, 2011, 222(1-2): 1-15.
[20] WANG Li-li, LU Chang hou. The effect of viscosity on the cavitation characteristics of high speed sleeve bearing[J]. Journal of Hydrodynamics, 2015, 27(3): 367-372.
10.1016/S1001-6058(16)60662-5
September 27, 2014, Revised March 9, 2015)
* Project supported by the National Science and Technology Major Project of China (Grant No. 2013ZX04013-011).
Biography: Zhi-feng LIU (1975-), Male, Ph. D., Professor
Qiang CHENG,
E-mail: chengqiangbjut@sina.cn
2016,28(4):585-595
猜你喜欢
杂志排行
水动力学研究与进展 B辑的其它文章
- Numerical investigation of unsteady cavitating turbulent flows around twisted hydrofoil from the Lagrangian viewpoint*
- Motion and deformation of immiscible droplet in plane Poiseuille flow at low Reynolds number*
- Design and development of guide vane cascade for a low speed number Francis turbine*
- Effect of some parameters on the performance of anchor impellers for stirring shear-thinning fluids in a cylindrical vessel*
- Prediction of oil-water flow patterns, radial distribution of volume fraction,pressure and velocity during separated flows in horizontal pipe*
- A parameter analysis of a two-phase flow model for supersaturated total dissolved gas downstream spillways*
