岩质边坡与锚喷支护结构相互作用的数值分析

2016-10-18李铁容沈俊喆

低碳世界 2016年26期

关键词：侧压力岩质面层

李铁容，沈俊喆

（1.湖南省地质灾害防治学会，湖南长沙410000；2.中南大学，湖南长沙410083）

岩质边坡与锚喷支护结构相互作用的数值分析

李铁容1，沈俊喆2

（1.湖南省地质灾害防治学会，湖南长沙410000；2.中南大学，湖南长沙410083）

以三峡库区湖北省秭归县高切坡防护工程项目为背景，针对不同类型岩体结构，运用大型有限元分析软件ANSYS，分别建立了全长粘结型锚杆—喷层—岩体相互作用有限元模型和自由段无粘结型锚杆—喷层—岩体相互作用有限元模型。对比分析结果表明：全长粘结型锚杆的自由段注浆能分担相当一部分侧向岩土压力，减轻锚喷面层受力。建议引入折减系数“k”对按现行规计算的岩石侧压力予以修正，并以此作为锚喷面层的设计荷载。给出了全长粘结型锚杆外锚头锚固长度的计算公式。

岩质边坡；锚喷支护；数值分析；喷锚面层；外锚头；锚固长度

1　引言

近年来，在岩质高切坡支护工程实践中，锚喷加固法因其具有良好的整治效果、可实施性强、施工简便、相比其他加固措施经济合理等而得到广泛应用。但由于目前对锚喷加固在高切坡支护中的作用机理尚未完全弄清，而且研究的重点主要放在锚杆的工作机理上，对锚杆—喷层—岩体相互作用的研究尚且不够深入，对考虑相互作用后锚喷面层的受力及锚杆外锚头的合理设计长度等尚未取得统一的认识。同时，由于我国的岩质边坡锚喷加固设计和施工规范为未能够建立，而现行《锚杆喷射混凝土支护技术规范》（GB50086-2001）实施对象主要为硐室，与边坡有着较大差别等等。因此，岩质高切坡锚喷加固的设计和施工在很大程度上要凭工程设计和施工人员的工程经验，具有较大的随意性，难以做到规范化。同时，也引起广大工程技术和研究人员的极大关注。

2　锚杆工作阶段的受力分析

2.1自由段无粘结型锚杆工作阶段受力分析

当锚杆的自由段不注浆或采取隔离措施时，称为自由段无粘结型锚杆。此时，因为岩体变形所导致的侧向岩土压力，均由锚喷面层进行承担。

2.2全长粘结型锚杆工作阶段受力分析

岩土体未变形时期，全长粘结型锚杆的自由段处于不受力状态，若是破裂面外岩土体出现变形并存在向自由面移动趋势，此时方会受力，侧向岩土压力的承担结构为自由段浆体、锚喷面层，即自由段浆体会分担一部分侧向岩土压力，从而减轻了锚喷面层的受力。

3　喷层-锚杆-岩体相互作用有限元分析

3.1ANSYS建模及参数选取

从锚杆受力分析可知，全长粘结型锚杆自由段浆体对锚喷面层或外锚头的受力具有分担作用，分担的比例与岩体类型、锚杆布置，施工工艺等有关。为了研究这些问题，本文通过ANSYS有限元分析软件，针对不同岩体类型，分别建立了全长粘结型锚杆和自由段无粘结型锚杆与喷层、岩体相互作用的有限元分析模型并进行了对比分析，得到了一些有益的结论。

3.1.1ANSYS建模

岩体与砂浆均用PLANE42平面单元，锚杆用LINK1杆单元，锚喷面层用beam3梁单元，锚杆与岩体之间的接触采用面面接触，接触对分别用targe169目标面单元和conta171接触面单元［1］，为简化计算，不考虑锚杆钢筋与砂浆体的滑移。

岩体本构关系采用弹塑性模型中的Drucker-Prager［2］模型。

3.1.2计算参数选取

Drucker-Prager模型要求输入弹性模量E、内摩擦角φ、岩土的粘聚力C、泊松比u四个指标。本文采用三峡库区常见的几类岩体物理力学指标参考值，如表1。锚杆、砂浆体及锚喷面层的物理力学指标如表2。

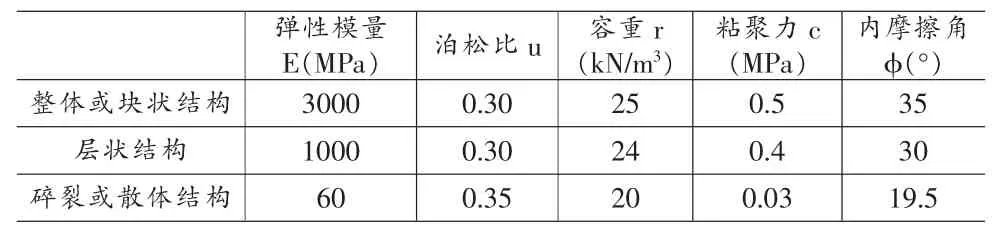
表1　三峡库区常见岩体结构的物理力学指标

表2　锚杆、砂浆体及锚喷面层的物理力学指标

3.2计算结果及分析

设按全长粘结型锚杆模型计算所得的锚喷面层计算截面上的弯矩为M有粘结，自由段无粘结型锚杆模型计算所得的锚喷面层计算截面上的弯矩为M无粘结，取k=M有粘结/M无粘结，则当岩体结构类型分别为整体或块状结构、层状结构、碎裂或散体结构时k沿坡面的变化情况如图1。

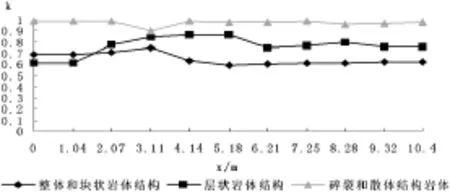
图1　两种模型锚喷面层计算截面上的弯矩比值k

从图1可以看出：在整体或块状结构的岩体中采用全长粘结型的锚杆时，其锚喷面层的弯矩值是自由段无粘结型的锚杆的0.59～0.75倍；在层状结构的岩体中采用全长粘结型的锚杆时，其锚喷面层的弯矩值是自由段无粘结型的锚杆的0.61～0.86倍，在碎裂或散体结构的岩体中采用全长粘结型的锚杆时，其锚喷面层的内力值是自由段无粘结型锚杆的0.90～0.99倍。显然，岩体完整性越好，全长粘结型锚杆自由段浆体分担锚喷面层的荷载的比例则越高，反之越低。因此，岩体结构类型是影响锚喷面层和外锚头受力的主要因素。

4　锚喷面层所受岩石侧压力与外锚头锚固长度计算

4.1锚喷面层上岩石侧压力

根据以上分析，结合规范［4］关于支护结构上岩石侧压力的计算方法，提出全长粘结型锚杆锚喷面层所受岩石侧压力的修正计算方法如下：

（1）岩石侧压力可视为均匀分布，修正后的岩石侧压力水平分力标准值按下式计算：

式中：e′hk——修正后的岩石侧压力水平分力标准值（kN/m2）；

E′hk——修正后的岩石侧压力合力的水平分力标准值（kN/m）；

H——边坡高度（m）。

（2）修正后的岩石侧压力合力的水平分力标准值可按下面两种情况计算：

①无外倾结构面的岩质边坡

式中：Ka——主动土压力系数；

H——边坡高度（m）；

γ——岩体重度（kN/m3）；

c——岩体粘聚力（kPa）；

φ——岩体内摩擦角（°）；

q——地表均布荷载标准值（kN/m2）；

δ——岩体对支护结构的摩擦角（°）；

β——填土表面与水平面的夹角（°）；

α——支挡结构墙背与水平面的夹角（°）；

θ——滑裂面与水平面的夹角（°）；

k——岩质边坡侧压力修正系数，整体或块状结构岩体时k取0.59～0.75；碎裂或散体结构时k取0.90～0.99。

②有外倾结构面的岩质边坡

式中：θ——外倾结构面倾角（°）；

cs——外倾结构面粘聚力（kPa）；

φS——外倾结构面内摩擦角（kPa）；

δ——岩石与挡墙背的摩擦角（°），取（0.33～0.5）φ0；

k——岩质边坡侧压力折减系数（k取0.61～0.86）；

其他符号同上。

4.2外锚头的锚固长度计算

外锚头的锚固长度取值在现行规范中没有明确说明，这就导致外锚头长度的取值具有很大的随意性。通过以上几节对全长粘结型锚杆在工作阶段受力特点的分析可知，锚杆自由段注浆可分担一部分侧向岩石压力，因此，锚喷面层传给锚杆外锚头的锚固力将减小，基于减小后的外锚头锚固力，本文提出全长粘结型锚杆外锚头锚固长度的计算式如下：