天津港地区土层剖面随机场特征参数的估计*

郭林坪　杨爱武　闫澍旺　侯晋芳

(①天津城建大学天津市软土特性与工程环境重点实验室　天津　300384) (②中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点试验室，天津市港口岩土工程技术重点试验室天津　300222) (③天津大学建筑工程学院　天津　300072)



天津港地区土层剖面随机场特征参数的估计*

郭林坪①②杨爱武①闫澍旺③侯晋芳②

(①天津城建大学天津市软土特性与工程环境重点实验室天津300384) (②中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点试验室，天津市港口岩土工程技术重点试验室天津300222) (③天津大学建筑工程学院天津300072)

天然地基或人工地基在形成过程中，不同位置的土由于成因相似，其物理力学特性指标具有空间自相关性，这种空间自相关性可以用随机场理论进行研究。为估计天津港地区土体物理力学性质的空间随机场特性，采用了现场钻孔取样、静力触探等方法获取了大量的描述土体物理力学性质的参数。由于静力触探试验能够连续取样以获得足够多的数据来进行随机场分析，文章主要应用静探数据检验了该地区土性指标的平稳性和各态历经性，指出应用Vanmarcke的随机场模型对土性指标进行分析具有可行性。本文的创新点在于探讨了天津港地区随机场模型的建立方法并应用改进的完全不相关距离方法估计了天津港地区典型土层剖面的随机场特征参数。为随机场理论应用于天津港地区岩土工程可靠度分析打下了坚实的基础。相同的方法可用于其他地区土层随机场特征参数的估计。

随机场特征参数天津港平稳性各态历经性相关距离折减函数

0　引　言

在岩土工程可靠度分析中，困难之处在于岩土参数的正确估计和土性剖面的概率模拟。将土层看成一个随机场是正确地模拟土体性质的前提，该随机场模型能够完成由试验数据求得的点特性到空间平均特性的过渡。

Lumb(1966)认为，理论上大部分的土性参数都可以认为是遵循正态或高斯分布的随机变量，所以在评价设计参数时基于正态分布建立统计方法是安全可行的。Vanmarcke(1977)建立了能够考虑土体空间自相关特性的随机场模型，并首次用“自相关距离”来描述土体的自相关性，给出了“自相关距离”的计算方法。Degroot et al.(1993)也对随机场理论在岩土工程中的应用作了深入研究，提出了用最大似然法来分析土质参数的空间变异性，并将最大似然法估计的现场十字板强度结果与传统矩估计结果进行了对比，证明了最大似然法分析土性参数空间变异性的可行性与合理性。Phoon et al.(2004)提出检验土层是否具有平稳性可以用改进的Bartlett统计法。其原理是通过对相关联样本函数进行仿真模拟，最终得到平稳性假设为真的检验标准。包承纲(1984)，包承纲等(1987，1996)对岩土参数的变异性及其分布规律进行了较为深入的研究，得到了大量的研究成果，引领了中国学者在岩土参数不确定性对岩土工程失效概率影响方面的研究。通过继续深入研究，朱红霞等(2007)提出了“完全不相关距离”的概念，并给出了确定方法，此外，通过对Lark(2002)研究成果的继续深入研究，他们还得到了计算时样本间距对相关距离的影响。杨勇等(2014)对西安黄土相关距离进行了计算，建立了西安各层黄土相关距离的概率模型，得到了可供该地区其他工程参考的代表值。张继周等(2014)对苏中腹地湖相沉积土层相关距离进行了统计分析，并获得了区域性代表值。在已有研究成果的基础之上，闫澍旺等(2014)首次对“完全不相关距离”确定折减函数的方法做出了改进。典型的随机场如图1 所示。

图1　典型随机场示意图Fig. 1　Schematic diagram of typical random field

对于图1，可以这样理解，对土体进行静力触探试验，将每一个钻孔的记录作为一个样本函数，最终得到的所有可能的样本函数总体的集合看作一个随机场，该随机场可表述为{y(z)}。其中，z表示深度。样本函数yi(z)的下标i(i=1， 2，…)表示随机过程的第i个样本函数。在某一位置z=z1，Y(z1)是随机变量，随机变量Y(z1)的第i个可能值用yi(z1)来表示。

本文将在前人研究成果基础之上，应用现场的静力触探数据检验该地区土性指标的平稳性和各态历经性，从而验证天津港地区土层剖面能否应用Vanmarcke模型进行分析，对天津港地区随机场模型的建立方法进行探讨，并应用改进的完全不相关距离方法(闫澍旺等， 2014)对天津港地区典型土层剖面的随机场特征参数进行计算，为随机场理论应用于天津港地区岩土工程可靠度分析做出贡献。

关于可靠度理论在岩土工程稳定性分析中的应用，最终的目标是要确定并提出适用于岩土工程可靠性评价的指标值，而不是盲目借用结构工程中的可靠指标值标准，因为结构工程中的材料与岩土工程中的材料——土的性质差别太大。但是到目前为止，由于地域性的差异及岩土参数的不确定性，要实现这一目标还有很长一段路要走。首先以天津港地区土性参数的随机场特性为研究重点，在后续研究工作中，应用提出的土层剖面随机场特征参数分析方法对大量工程(包括稳定的和已经发生破坏的工程)的稳定性进行评价，确定各工程对应的可靠指标值，由稳定工程对应的可靠指标值的范围及破坏工程对应的可靠指标值范围确定可靠指标标准值，然后将这种方法进行推广，逐步、逐阶段的实现最终目标。

1　计算工程现场情况

与常规勘探手段相比，静力触探能够连续地取得土性参数，较连续地反映土层剖面的情况，且静力触探具有快速、经济、节省人力等优点(黄文熙， 1983)。因此对此场地的40个静力触探孔的数据进行分析，用以确定各土层的相关距离、完全不相关距离，进而确定各土层土性指标的方差折减函数。图2、图3分别为静力触探现场情况及静力触探孔布置情况。

图2　静力触探现场情况Fig. 2　Local conditions of static cone penetration test

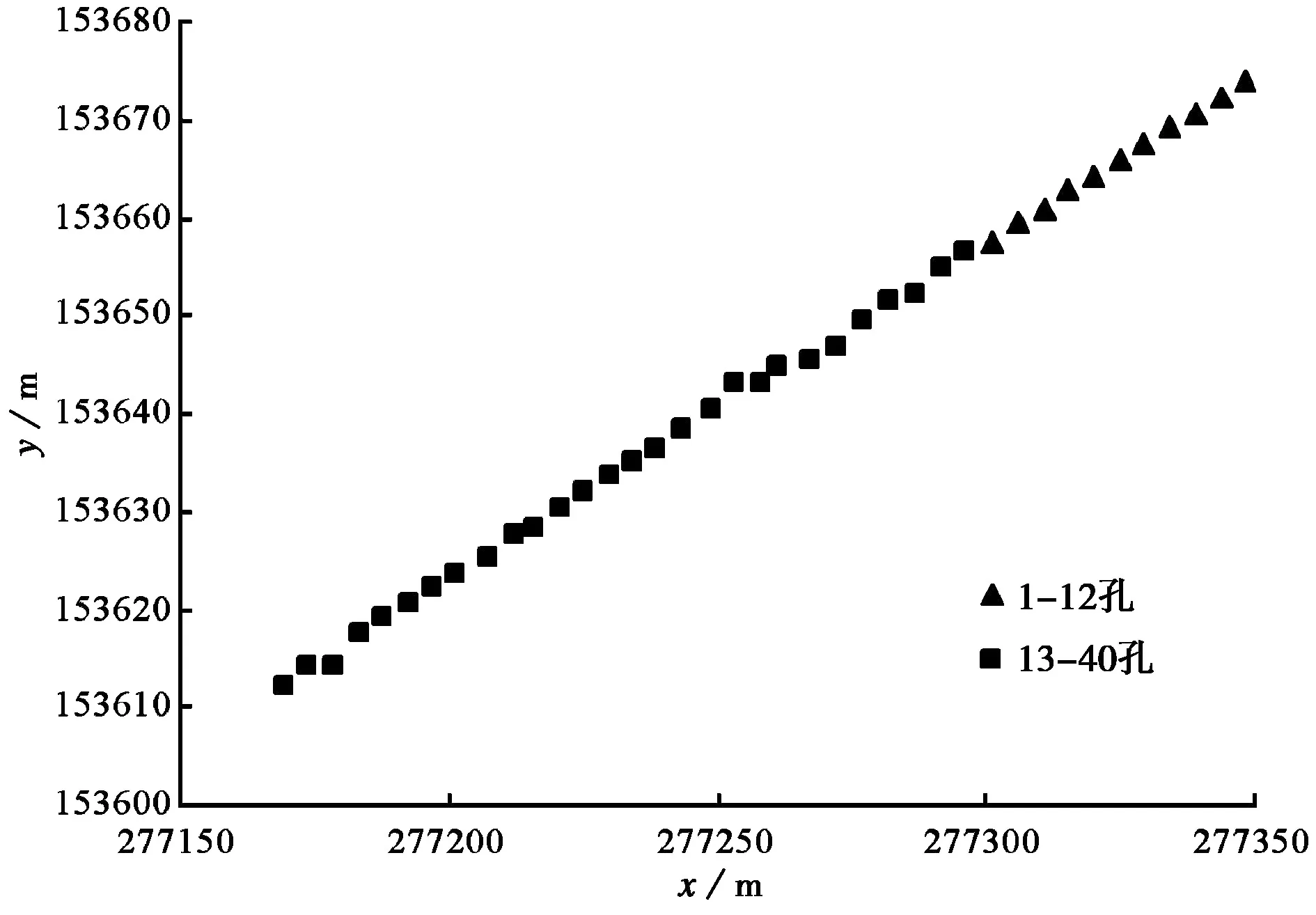
图3　静力触探孔布置情况Fig. 3　Distribution of static cone penetration tests

由于篇幅所限，以其中4个静力触探孔的贯入曲线为例以示土层划分依据，图中深度为纵坐标，锥尖阻力为横坐标(图4)。

图4　静力触探曲线Fig. 4　Static cone penetration test curvesa. 1号孔静探曲线； b. 2号孔静探曲线； c. 3号孔静探曲线； d. 4号孔静探曲线

按照锥尖阻力曲线特征对土层进行分层的依据如表1所示：

表1　锥尖阻力曲线特征Table1　Characteristics of probe resistance

土层锥尖阻力与深度关系曲线特征淤泥和淤泥质黏性土锥尖阻力值较小,且贯入曲线平缓,无突变现象黏土及粉质黏土锥尖阻力值较大,有缓慢的波状起伏,当土层中存在结核时贯入曲线会呈现突变现象,锥尖阻力正负相差10%～20%粉土贯入曲线起伏较大,曲线的峰值、谷值呈圆形,变化频率不是很大,锥尖阻力正负相差30%～40%

依据现场获得的静力触探贯入曲线线型，并结合钻孔资料及地区经验，对土层进行划分。经分析可知由地表向下20m范围内由上到下土层依次为：淤泥层、淤泥质黏土层、粉质黏土层。

2　平稳性和各态历经性的检验

贾晓黎(1985)、闫澍旺等(1995)提出土性剖面是否符合平稳性和各态历经性是判定能否应用Vanmarcke提出的随机场模型对土性指标进行分析的前提，并应用静力触探比贯入阻力曲线上的数据对土性的平稳性和各态历经性进行了检验。之后，张梅等(2001)对这一结论进行了验证和补充，指出当土性剖面不具有平稳性和各态历经性，即当土层层位变化大或层内薄夹层多时，Vanmarcke提出的随机场模型是不适用的。

因此在建立天津港地区土性剖面随机场模型之前，首先要对其平稳性和各态历经性进行检验。在分析过程中，应用平稳性和各态历经性的定义对静力触探试验数据进行检验。检验结果如图5，图6 所示。

图5　土层的平稳性检验结果Fig. 5　Inspection result of stationary of soila. 淤泥层的平稳性检验结果； b. 淤泥质黏土层的平稳性检验结果； c. 粉质黏土层的平稳性检验结果

从图5 中可以看出，被检验的土性指标的集平均和相关函数基本都在一条与横坐标轴平行的直线上轻微摆动，说明被检验随机场的各样本函数的集平均和相关函数在概率意义上都不随深度变化。因此可以认为该土性剖面随机场具有平稳性。

图6　土层的各态历经性检验结果Fig. 6　Inspection result of ergodicity of soila. 淤泥层的各态历经性检验结果； b. 淤泥质黏土层的各态历经性检验结果； c. 粉质黏土层的各态历经性检验结果

从图6 中可以看出，被检验的土性指标的集平均和相关函数基本都在一条与横坐标轴平行的直线上轻微摆动，说明被检验随机场的各样本函数的集平均和相关函数在概率意义上都不随水平间距变化。因此可以认为该土性剖面随机场具有各态历经性。

以上平稳性和各态历经性的检验都是针对沿深度方向上的土性剖面，即竖直方向的土性剖面随机场。如果考虑水平方向的土性剖面随机场，按照平稳性和各态历经性的定义及检验方法可以看出：竖直方向上土性剖面的平稳性就是水平方向土性剖面的各态历经性； 竖直方向上土性剖面的各态历经性就是水平方向土性剖面的平稳性。因此，可以得到这样的结论：对于该随机场来说，竖直方向上是平稳的且具有各态历经性，水平方向上同样是平稳的且具有各态历经性。

3　天津港地区典型土层的随机场特征参数

应用相关函数法计算淤泥层、淤泥质黏土层及粉质黏土层在竖直方向上的相关距离值(Yan et al., 2015)，其均值和标准差结果如表2所示。

表2　各土层相关距离值Table2　Scales of fluctuation of soil layers

相关距离值淤泥层淤泥质黏土层粉质黏土层均值0.3170.8080.356标准差0.2370.3680.072

应用改进的完全不相关距离计算方法估计天津港地区典型土层的随机场特征参数，表3即为改进之后的方差折减函数的确定原则。

表3　方差折减函数的确定原则Table 3　Determination of non-correlation arrange

相关函数ρ(Δz)方差折减函数Г2(h)δu≤L≤h*L≥h*L≤δu单指数型ρ(τ)=e-bτ2b2h2(bh+e-bh-1)(其中,h=L)0.1801指数余弦型1ρ(τ)=e-bτ·cos(bτ)1b2h2[bh-e-(bh)sinbh](其中,h=L)0.4691指数余弦型2ρ(τ)=e-bτ·cos(ωτ)δuh+δuh()2α1-e-h/α2δuα3sinhα4δu+α5coshα4δu()[](其中,ω/b=α,α1=(α2-1)/2,α1=(α2+1)/2,α3=α,α4=2α/(α2+1),α5=α2-1,h=L)同左式(其中,h*=h)1

注：表中ω、b均为相关函数中的待定参数，可在相关函数拟合过程中确定应用完全不相关距离方法估计方差折减函数的过程如下：

(1)首先确定相关函数的型式，并计算相关距离δu的值。

(2)然后依据Vanmarcke(1977)提出的式(1)及所确定的相关函数分别绘制Г2(h)～h/δu曲线。

(1)

(3)找到两曲线的交点，由此交点n*就能确定完全不相关范围L*=n*δu(图7)，从而能够得到完全不相关距离值h*=L*/2，即在计算折减函数时用于平均的空间范围。

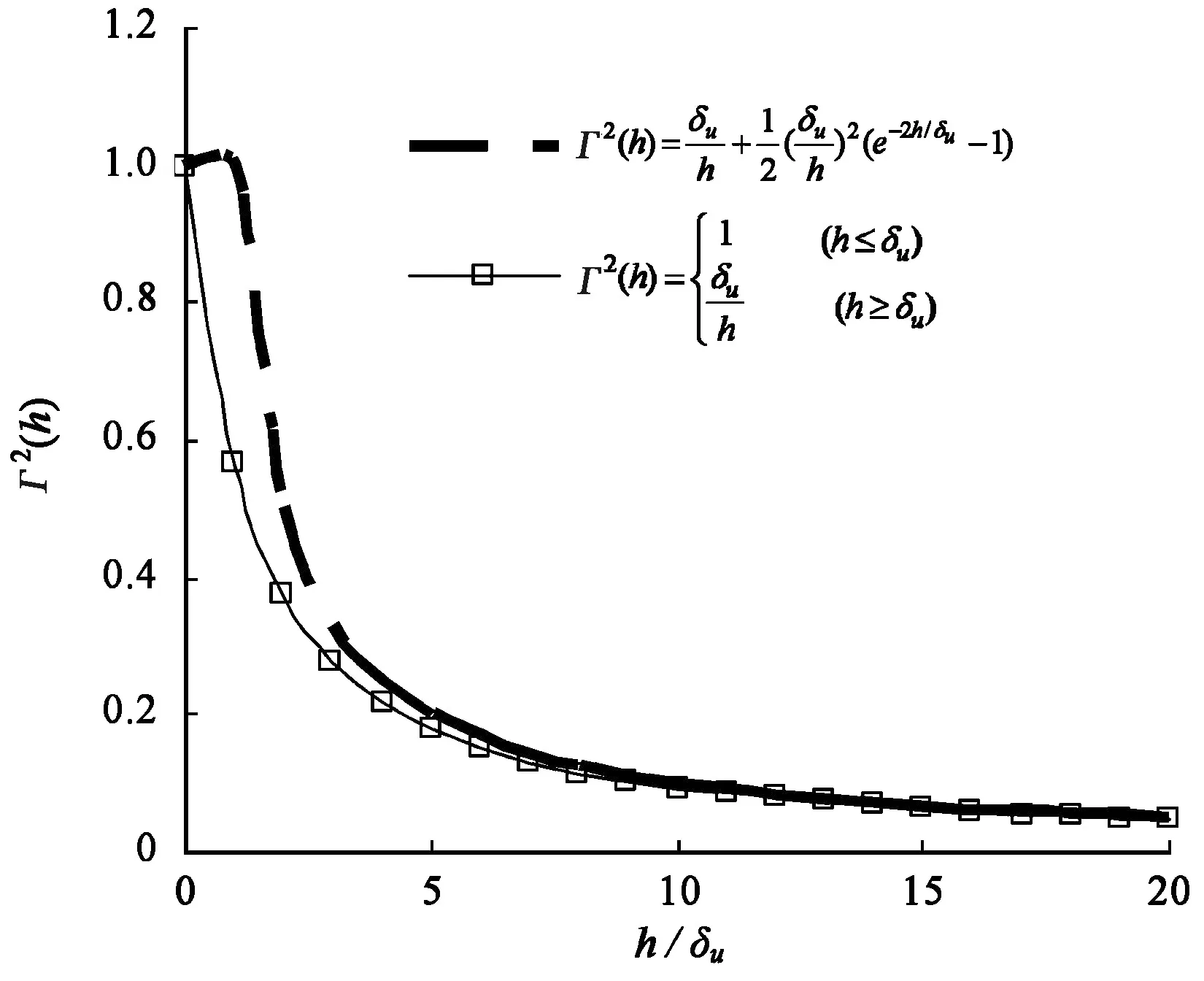
图7　完全不相关范围的确定Fig. 7　Determination of non-correlation arrange

表4　天津港地区典型土层的随机场特征参数Table4　Random field’s characteristic parameters of typical soil layers in Tianjin Port

土层名称ω/b方差折减函数值Γ2(h)淤泥0.170.353淤泥质黏土0.210.379粉质黏土0.380.378

(4)折减函数值可以通过相关距离δu与完全不相关距离h*的比值求得，即Γ2(h)=δu/h*。

按照上述计算过程估计天津港地区典型土层的随机场特征参数值，各土层的完全不相关距离值及方差折减函数值计算结果如表4所示：

应用改进的相关函数法计算了各土层竖直方向上的相关距离值，并进一步应用改进的完全不相关距离方法确定了天津港地区典型剖面的随机场特征参数，该地区20m深度范围内土层的方差折减函数值在0.35～0.40之间，该结果可以作为本地区岩土工程设计及稳定性评价的参考，并在获得适用于岩土工程可靠性评价指标值的道路上又向前迈进了一步。

4　结　论

探讨了天津港地区随机场模型的建立方法，并估计了天津港地区典型土层剖面的随机场特征参数，为随机场理论应用于天津港地区岩土工程可靠度分析打下了坚实的基础。得到的主要结论如下：

(1)平稳性和各态历经性检验的结果表明，对于天津港地区，可以应用Vanmarcke提出的随机场模型对土性指标进行分析。

(2)分析结果表明，对于土性剖面随机场模型，竖直方向上是平稳的且具有各态历经性，水平方向上必然是平稳的且具有各态历经性。

(3)建立了天津港地区随机场模型，并应用改进的完全不相关距离方法对天津港地区典型土层的随机场特征参数进行了估计，该地区20m深度范围内的土层的方差折减函数值在0.35～0.40，可以作为本地区其他岩土工程设计及稳定性评价的参考。

Bao C G. 1984. Problem in reliability design in geotechnic[J]. Yangtze River， (1)： 8～15.

Bao C G，Yu L. 1987. The Probabilistic method of stability analysis for soil slope in under unusual condition[J]. Chinese Journal of Geotechnical Engineering， 9(3)： 16～26.

Bao C G，Gao D Z，Zhang Q H. 1996. Research on method for reliability analysis on foundation engineerings [M]. Wuhan： Wuhan Technical University of Surveying and Mapping Press．

Degroot D J， Baecher G. 1993. Estimating autocovariance of in-situ soil properties[J]. Journal of Geotechnical Engineering， ASCE，119(1)： 147～165.

Gao D Z. 1989. Reliability theory of soil mechanics[M]. Beijing： China Architecture & Building Press．

Huang W X. 1983. Engineering properties of soil[M]. Beijing： Water Resources and Electric Power Press．

Jia X L. 1985. Analysis on application and properties of random field of soil profile[D]. Tianjin： Tianjin University．

Lark R M. 2002. Optimized spatial sampling of soil for estimation of the variogram by maximum likelihood[J]. Geoderma，105(1-2)： 49～80.

Lumb P. 1966. The variability of natural soils[J]. Canadian Geotechnical Journal，3(2)： 74～97.

Phoon K K，Quek S T，An P. 2004. Geostatistical analysis of cone penetration test(CPT)sounding using the modified Bartlett test[J]. Caradian Geotechnical Journal，41(2)： 356～365.

Vanmarcke E H. 1977. Probabilistic modeling of soil profiles[J]. Journal of the Geotechnical Engineering Division， ASCE， 103(11)： 1227～1246.

Yan S W，Jia X L，Guo H Z. 1995. Examination of stationarity and ergodicity on soil profile[J]. Chinese Journal of Geotechnical Engineering，17(3)： 1～9.

Yan S W，Guo L P, Cao Y H. 2014. Kegularity of determination of reduction function of variance in reliability analysis of geotechnical Engineering[J]. Rock and Soil Mechanics，35(8)： 2286～2292.

Yan S W，Guo L P. 2015. Calculation of scale of fluctuation and variance reduction function[J]. Transaction of Tianjin University，21(1)： 41～49．

Yang Y，Zhang H F，Fan W，et al. 2014. Statistical distribution characteristics of correlation distance of Xi’an loess[J]. Journal of Engineering Geology，22(1)： 160～165．

Zhang J Z，Miao L C，Lin F，et al. 2014. Statistical analysis of correlation distances of lacustrine sedimentary soils in central region of Jiangsu Province[J]. Journal of Engineering Geology，22(2)： 348～354．

Zhang M，Zhang J，Yang Z，et al. 2001. The research on vanmarcke model’s application[J]. Journal of Agricultral university of Hebei，24(3)： 79～82.

Zhu H X. 2007. Study of using random field theory in soil foundation reliability analysis[D]. Tianjin： Tianjin University．

Zhu H X，Yan S W. 2007. Random field model and reliability analysis of foundation soil in Tianjin Port[J]. Chinese Journal of Rock Mechanics And Engineering， 26(S2)： 3959～3965.

包承纲. 1984. 土工中的可靠性设计问题[J]. 人民长江， (1)： 8～15.

包承纲，于丽. 1987. 土坡在非常条件下稳定分析的概率方法[J]. 岩土工程学报， 9(3)： 16～26.

包承纲，高大钊，张庆华. 1996. 地基工程可靠度分析方法研究[M]. 武汉：武汉测绘科技大学出版社．

高大钊. 1989. 土力学可靠性原理[M]. 北京：中国建筑工业出版社．

黄文熙. 1983. 土的工程性质[M]. 北京：水利电力出版社．

贾晓黎. 1985. 土性剖面的随机场特性及其应用研究[D]. 天津：天津大学．

闫澍旺，贾晓黎，郭怀志. 1995. 土性剖面随机场模型的平稳性和各态历经性验证[J]. 岩土工程学报，17(3)： 1～9.

闫澍旺，郭林坪，曹永华. 2014. 岩土工程可靠度分析中方差折减函数确定的一般规律[J]. 岩土力学，35(8)： 2286～2292.

杨勇，张海峰，范文，等. 2014. 西安黄土土性相关距离的统计分布特性研究[J]. 工程地质学报，22(1)： 160～165．

张继周，缪林昌，林飞，等. 2014. 苏中腹地湖相沉积土层相关距离的统计分析[J]. 工程地质学报，22(2)： 348～354．

张梅，张靖，杨谆，等. 2001. Vanmarcke模型适用性探讨[J]. 河北农业大学学报，24(3)： 79～82.

朱红霞. 2007. 随机场理论在地基可靠度分析中的应用研究[D]. 天津：天津大学．

朱红霞，闫澍旺. 2007. 天津港地基土随机场特性及可靠度分析[J]. 岩石力学与工程学报，26(S2)： 3959～3965.

ESTIMATION OF RANDOM FIELD CHARACTERISTIC PARAMETERS OF SOIL LAYERS AT TIANJIN PORT

GUO Linping①②YANG Aiwu①YAN Shuwang③HOU Jinfang②

(①KeyLaboratoryofSoftSoilEngineeringCharacterandEngineeringEnvironmentofTianjin，TianjinChengjianUniversity，Tianjin300384) (②CCCCTianjinPortEngineeringInstitute，Ltd.，KeyLaboratoryofPortGeotechnicalEngineering，MinistryofCommunications，PRC，KeyLaboratoryofGeotechnicalEngineeringofTianjin，Tianjin300222) (③SchoolofCivilEngineering，TianjinUniversity，Tianjin300072)

The environment and conditions for both natural and artificial soilsat different places are similar. Therefore physical and mechanical properties of soil samples are relevant. The relevance can be analyzed with random field theory. To estimate spatial characteristics of physical and mechanical properties of soil in Tianjin Port， tests such as boring in situ and standard cone penetration are employed to acquire enough test data that are essential to the employment of random field theory. Because it can continuously obtain enough data， the standard cone penetration test is the main method to get test data. The data is used to inspect the stationary and ergodicity of this area. Results show that the random field model put up by Vanmarcke can be employed in this research. In this paper， the innovation points include that the method establishing random field model in Tianjin Port is discussed and the characteristic parameters of typical layers in this area are estimated with the improved non-correlation method. The result can lay a solid foundation for reliability analysis in geotechnical engineering in Tianjin Port. This method of estimating characteristic parameters of random field can be used for other areas．

Random field characteristic parameters， Tianjin Port， Stationary， Ergodicity， Scale of fluctuation， Variance reduction function

10.13544/j.cnki.jeg.2016.01.016

2014-11-13;

2015-03-09.

天津城建大学科研启动项目(64-05140206)，港口岩土工程技术交通行业重点实验室开放课题基金(14-50)，国家自然科学基金(41372291)，天津市科技计划项目(15JCZDJC40600，15ZCDSF00220)资助.

郭林坪(1986-)，女，博士，讲师，岩土工程专业. Email: guolinping1986@163.com

简介： 杨爱武(1971)，男，博士，教授，岩土工程专业. Email: tulilab@163.com

TU441

A