基于RSSI的测距研究
2016-10-18陈磊,刘伟
陈 磊, 刘 伟
(湖北工业大学 计算机学院, 湖北 武汉 430068)
基于RSSI的测距研究
陈磊, 刘伟
(湖北工业大学 计算机学院, 湖北 武汉 430068)
基于RSSI信号传播理论模型. 分析信号传播理论模型中的射频参数因子分别对信号传播和测距精度的影响。采用最小二乘法对实验采集的数据进行曲线拟合得到RSSI-d关系曲线和公式。
RSSI; 无线传感器网络; 信号传播理论模型
传感器网络定位技术是大多数无线传感器网络应用中的关键技术,而基于测距的定位技术都是通过采集锚节点与目标节点之间的距离来完成定位的,因此,对于无线传感器网络节点之间的距离研究是十分重要的。常见的基于测距的定位算法中有基于信号接受强度(received signal strength indicator,RSSI)、时间到达(time of arrival,TOA)、时间差到达(time different of arrival,TDOA)和角度到达(angle of arrival,AOA)等技术[1-3]。
由于RSSI测距技术成本低廉,不需要很多的硬件设备来进行测量,并且大多数的通信设备携带的通信模块可以直接提取RSSI值,所以,其应用相当广泛。本文主要针对信号传播理论模型中的参数因子对RSSI值与距离之间的关系进行研究,最后通过最小二乘法对其关系进行曲线拟合得到RSSI-d之间关系[4]。
1 RSSI信号模型建立
RSSI测距算法即信号接受强度指引方法,根据节点之间接受信号的强度,通过信号传播理论模型或经验模型将传播过程中衰弱的信号强度转化为两节点间的位置信息。
RSSI测距技术中,一般采用信号传播理论模型来建立RSSI值与距离之间的关系[5]。用Pr表示信号接受功率,Pt表示信号发射功率,d表示两节点之间的距离, 信号发射功率与信号接受功率之间有如下关系:
Pr=Pt/dn
(1)
在式(1)两边取对数关系得到
10nlgd=10lg(Pr/Pt)
(2)
由于信号发射功率已知,将式(1)带入式(2)中得到
10lgPr=-(A+10nlgd)
(3)
在式(3)左边,10lgPr是接受信号功率转化为dBm表达式,所以直接转化为式(4)
RSSI(dBm)=-(A+10nlgd)+Xσ
(4)
在式(4)中可以看到,信号强度与距离之间的关系受到参数A和n的影响。而射频参数A是表示距离信号发射1 m处所接受到的信号功率的绝对值。以dBm表示。如在1 m处接受的平均能量为-42 dBm,就设置A为40。而射频参数n表示信号动态衰弱因子,表示随着信号传播距离的增加, 其功率衰弱的速度[6],这个参数与周围环境有着密切关系,一般在2~6之间。而信号接受强度的衰减一般与dn成比例。在理想的情况下,信号的长期衰落是服从对数正态分布的。
2 射频参数因子分析
从式(1)~(4)可以看出,RSSI值与距离d之间的关系主要受参数A和n的影响。为了分析RSSI-d曲线与其之间的关系,分别对两个因子进行讨论分析。
当A不变,n发生改变时,信号接受强度与两节点之间距离值的曲线关系如图1。
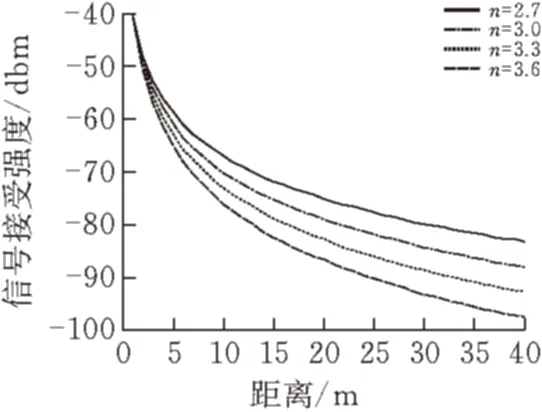
图 1 参数变化曲线图
由图1可以看到,当n取值越小时,信号在传播过程中衰减越小,信号传播的距离越远。传播因子n主要受到信号传播时的衰减、多经、反射等影响,而在室内环境中,则受到墙壁、地面等折射、反射的干扰。在不同的环境之中,传播因子n也是不一样的,这些因素都是随机、动态的。当这些干扰越小时,传播因子也越小,传播距离也会越远,RSSI测距精度也会越高。
当n不变,A发生改变时,信号接受强度与两节点之间距离值的曲线关系见图2。
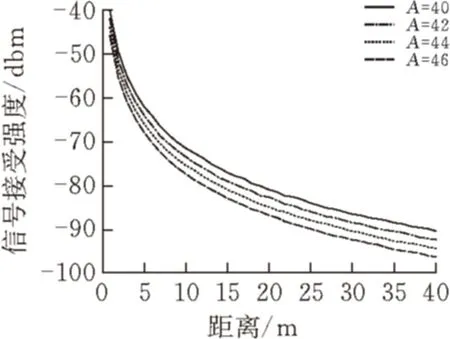
图 2 参数变化曲线图
由图2可以看到,当近距离传播时,信号衰减尤为明显,而随着距离增加,信号传播衰减比较平缓,呈缓慢线性衰落。当发射信号功率增加时,增加的传播距离可以近似为发射信号功率增加量和曲线在平缓阶段的斜率的比值。
3 最小二乘法RSSI-d曲线拟合处理
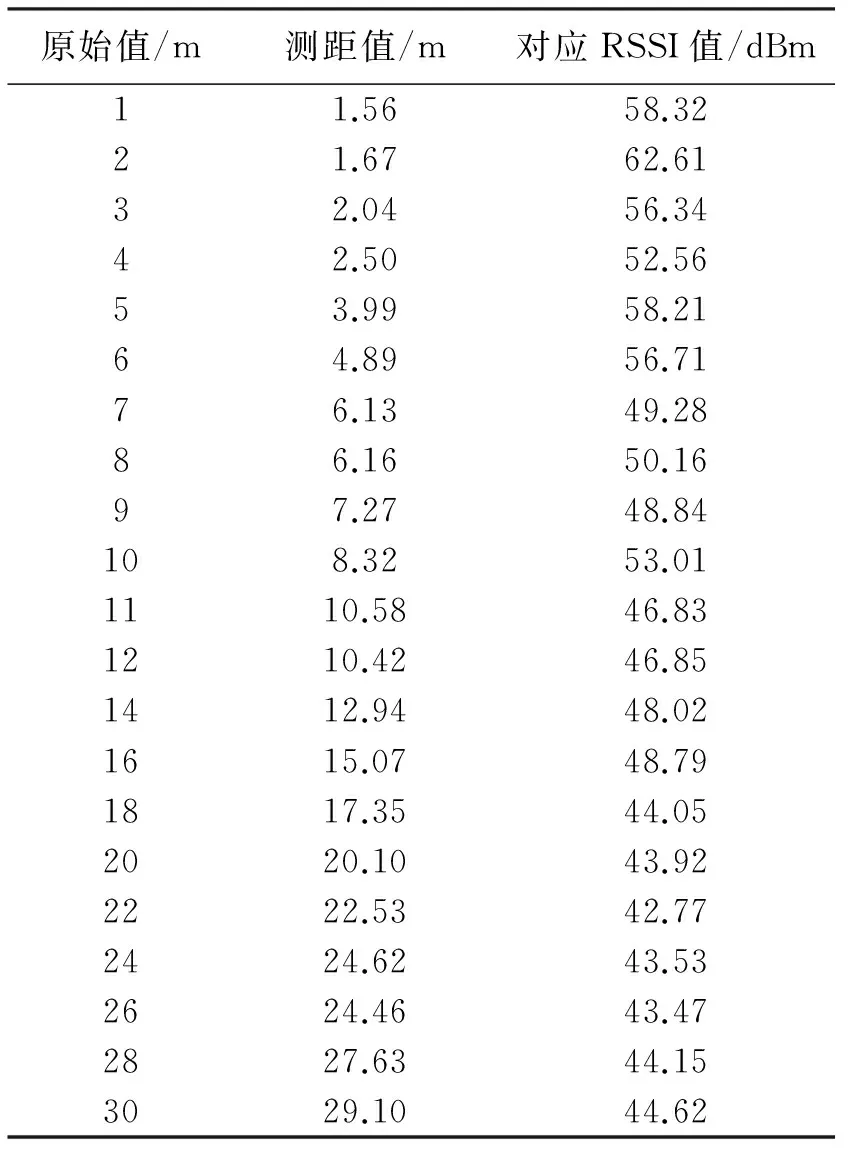
为了进行室外测距测试,选取了大运动场作为实验场景。选取运动场作为本系统的实际测试环境,有一定的代表性。在实际实验场景中采集数据,制作RSSI-d映射表,原试验数据映射表见表1。
通过得到的数据散点进行曲线拟合,采用最小二乘法[7]。拟合曲线公式采用式(3)。原试验数据与拟合曲线见图3,在图中可以明显看到,基于RSSI测量方法获取的试验数据与真实值之间还是存在一定差异,实验数据分布于曲线周围。
曲线拟合公式为:
RSSI(dBm)=-13.094lgd+61.943 (5)
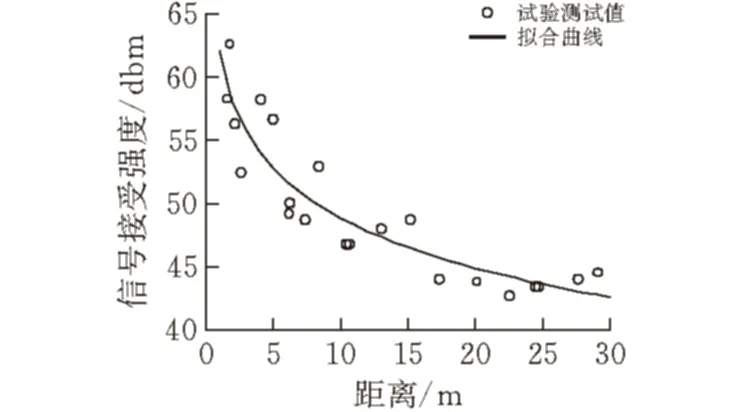
图 3 最小二乘法拟合曲线图
4 结束语
当前,无线传感器网络定位技术的研究越来越多,而对于其关键技术——测距技术的研究也显得尤为总要。本文以RSSI测距技术为基础,主要针对其中的信号传播理论模型进行研究,讨论了其中两个射频参数对RSSI-d曲线的影响。最后通过实际场地测试,运用最小二乘法对实验采集的散点进行曲线拟合,得到RSSI-d之间的关系曲线和公式。
[1]冒熙蒙. 基于测距技术的无线传感器网络定位算法及应用[D]. 上海:上海交通大学, 2013.
[2]Chan F K, Wen C Y. Adaptive AOA/TOA localization using fuzzy particle filter for mobile WSNs[C].Vehicular Technology Conference (VTC Spring), 2011 IEEE 73rd. IEEE, 2011: 1-5.
[3]熊志广. 基于 RSSI 的无线传感器网络定位算法研究及应用[D]. 重庆: 重庆大学, 2010.
[4]Wang H, Wan J, Liu R. A novel ranging method based on RSSI [J]. Energy Procedia, 2011, 12: 230-235.
[5]信召建. 基于RSSI值的无线传感器网络定位技术研究[D]. 哈尔滨:哈尔滨工业大学, 2012.
[6]王学. 基于RSSI带误差补偿的无线传感器网络定位算法研究及实现[D]. 洛阳:河南科技大学, 2013.
[7]陶为戈, 朱昳华, 贾子彦. 基于RSSI混合滤波和最小二乘参数估计的测距算法[J]. 传感技术学报, 2012, 25(12):1748-1753. DOI:10.3969
[责任编校: 张岩芳]
RSSI-based Research on Ranging
CHEN Lei,LIU Wei
(SchoolofComputerScience,HubeiUniversityofTechnology,Wuhan430068,China)
Research has revealed that the correlation between distance and RSSI (Received Signal Strength Indication) values is the key of ranging and localization technologies in wireless sensor networks (WSNs). In this paper, the ranging technology was discussed based on RSSI signal transmission theoretical model. Then, the effects of the signal propagation and ranging accuracy were analyzed with RF parameters. Finally, the least squares curve fitting the experimental data was used to obtain the RSSI-d curve and formula.
RSSI; WSNs; Signal Transmission Theoretical Model
2015-05-19
湖北省武汉市科技攻关项目(201210421134)
陈磊(1990-), 男, 湖北武汉人,湖北工业大学硕士研究生,研究方向为无线传感器网络
1003-4684(2016)04-0080-03
TP393
A
