健壮性通信网络的抗毁性

张小萌， 文昌俊

(1 湖北工业大学机械工程学院， 湖北 武汉 430068； 2 湖北省现代制造质量工程重点实验室， 湖北 武汉 430068)



健壮性通信网络的抗毁性

张小萌1，2， 文昌俊1，2

(1 湖北工业大学机械工程学院， 湖北 武汉 430068； 2 湖北省现代制造质量工程重点实验室， 湖北 武汉 430068)

以全连通网络为参考标准，以最短路径数为评价指标，建立健壮性通信网络的抗毁性模型，利用MATLAB提出一种新的计算最短路径数的方法，通过实例进行计算，得出网络的抗毁性。研究发现，拓扑结构越对称，健壮性通信网络的抗毁性越好。

抗毁性； 拓扑结构； 最短路径数； 健壮性通信网络； MATLAB

若干个拓扑节点构成的大型无线通信系统，使网络节点间的信息交换以及传递更加快速、准确和方便。为了保证信息准确快速传递，对健壮性网络可靠性的要求特别严格。但在网络使用过程中，由于自然条件或者人为破坏，某些节点或是某些链路断开可能严重影响到网络拓扑结构的可靠性。抗毁性作为评价健壮性通信网络可靠性的一个重要性能指标，在设计网络的拓扑结构时应该把网络的抗毁性考虑在其中。同时只有通过网络抗毁性的计算，设计者才可知道网络拓扑结构中有哪些节点和边是比较重要的，需要进一步加固，使其不被外部条件破坏。

网络抗毁性[1]一直是一个热门问题，很多外国学者从连通度、粘聚度、中心度等方面着手分析，然而网络抗毁性一直都是一个NP完全问题。Douglas R.White 和 Frank Harary提出了网络连通度和凝聚度等问题[2]，另外Douglas R.Shier[3]基于图理论提供了一种计算网络可靠性的方法，Manchester.J[4]等人提出交通网络的抗毁性。国内的相关研究方向分为两种：一是基于节点分析，如节点重要性评估，有生成树法、网络凝聚度等；二是基于全网的抗毁性分析，如删除后最短路[5]。陈建[6]用均方差来度量节点的抗毁性值；郭伟[7]提出跳面节点法来研究通信网络的抗毁性；赵静娴[8]提出基于不重叠路径数的标准稳定熵指标来评价网络抗毁性；魏福林[9]提出利用基于最小割集来衡量网络的抗毁性；饶育萍[10]提出利用最短路径来评价网络抗毁性。

1　健壮性通信网络的抗毁性评价

1.1参考标准

对于一个无向连通图G=(V,E)，用集合V={v1,v2,v3,…,vn}表示无向连通图的点集合。用集合E={e1,e2,…,e3}表示边的集合。

定义1全连通图：无向连通图中，对于任意两点vi和vj之间都有直接连接的图(图1)。否则，则称为非连通图。

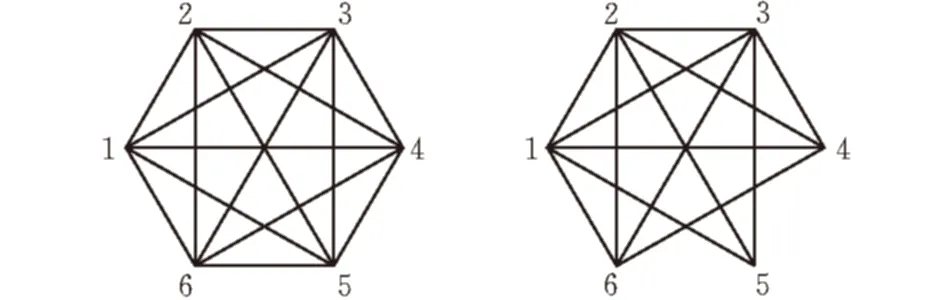
图 1　全连通图　　　　图 2　非全连通图

由图1可以看出，依据抗毁性概念，对于有N个节点的全连通图而言，任意去掉小于N-1个节点或者N-1边，拓扑图都是连通的，因此可以得出在所有网络拓扑结构中抗毁性最强的是全连通网络。另外，全连通图分布均匀，对称性强，结构紧凑，任意两节点之间都能直接连接。但是在实际生活中，大多数通信网络都是非全连通的(图2)，主要是因为建立全连通网络所耗费用较大。在实际网络中，像通信网络、社交网络以及交通网络等大型网络都是在全连通网络的基础上改进的。因此，全连通网络经常被作为评价实际网络抗毁性的参考标准。

1.2评价方法

跳面节点法[6]论及评价网络抗毁性的方法，因为侧重点不同，评价方法有所差异，不适用于一些特殊的拓扑结构。例如在基于最小路径数的网络抗毁性中，文献[10]指出了错误之处。

例如图3所示的拓扑结构,当结构中存在多个割点时，利用生成树法判断节点的重要性就不准确。拓扑结构中3、4节点都是割点，利用生成树方法判断可知，不论是3节点还是4节点失效，都将造成拓扑结构不连通且生成树数目均为0。所以，对于图3所示的拓扑结构而言，节点3和4是同等重要。但很明显，节点4上所连接的分支比节点3所连接的分支多，因此，在此拓扑结构中利用生成树评价节点的重要性是不准确的。

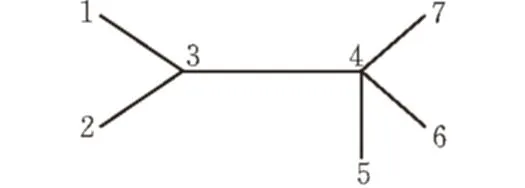
图 3　多割点图

总结以上方法的不足，发现各个节点之间的信息传递，跳数较多的比跳数少的路径可靠性差。另外，只有在最短路径被破坏的情况下，系统才会选择走相对较长的路径。一个健壮性通信网络中，最短路径的数量越多，拓扑结构越紧凑，这个网络的抗毁性就会越高。所以本文把最短路径作为评价抗毁性的一个重要指标。因此，只要找到拓扑图最短路径的数量，就可以评价实际网络拓扑结构的抗毁性。

对于N节点的拓扑结构的网络，将节点vi到vj之间跳数最少的路径称为最短路径[9]。

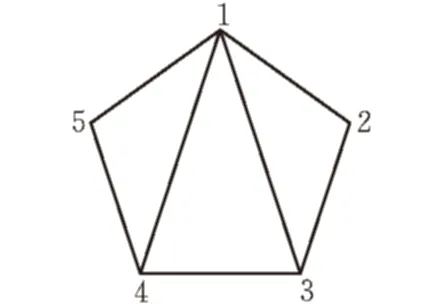
图 4　简单拓扑结构图

对于图4而言，任意两点之间条数为1的最短路径数量为7，分别为：v1→v2，v1→v3，v1→v4，v1→v5，v2→v3，v3→v4，v4→v5；任意两点跳数为2的最短路径数为3，分别为：v2→v4，v2→v5，v3→v5。

2　网络的抗毁度函数

2.1健壮性网络的抗毁性理论模型

本文以最短路径作为评价指标，全连通网络作为评价标准，基于上述分析推出网络抗毁性函数

(1)

式中：I为网络的抗毁性；在节点总数为N的条件下，X为实际健壮性通信网络拓扑结构中任意vi和vj两点的之间的最短路径总数，且

(2)

Y为全连通网络拓扑结构中任意vi和vj两点的之间的最短路径总数。

根据经验公式可知，节点数为N的全连通网络最短路径数

(3)

式中：k表示跳数；Y(k)表示节点vi到vj之间跳数不大于k的所有路径数。

全连通网络任意两点之间的路径总数

(4)

式中：抗毁性I以百分比表示，其越趋近于0，网络拓扑结构抗毁性就越低；I越趋近于1，网络拓扑结构抗毁性就越高。

2.2健壮性网络的抗毁性求解

为了求取网络的抗毁性，必须先求出X,Y,和Q,由于已知实际健壮性网络拓扑结构中节点数N，由式(3)、(4)可分别求出Y和Q。因此，现在要解决的是要求出实际健壮性网络最短路径数X。由于实际健壮性通信网络的拓扑结构都比较复杂，节点多，利用饶育萍提出的邻接阵的k次幂的方法求最短路径比较耗时。另外，求最短路长的方法还有现在使用比较普遍的D算法和F算法[11]，但这两种算法只能求最小路径的长度，不能求最短路径数的数量。因此，本文在D算法和F算法的基础上，改进了D算法和F算法，利用MATLAB软件编程，在MATLAB的输入端口，输入实际健壮性通信网络的邻接阵，可以求出任意两点之间的最短路径数量。此方法不论网络拓扑是多么复杂，都可以快速利用计算机得到抗毁性的数值。

3　实例分析

分析图5、图6的网络抗毁性。

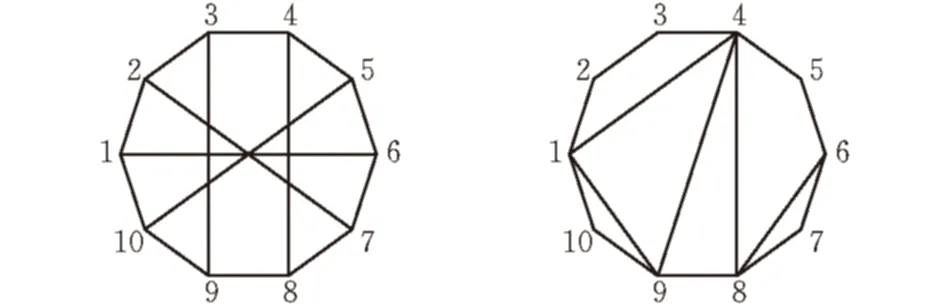
图 5　连通图G1　　　　　图 6　连通图G2

G1(10,15)的邻接阵

G2(10,15)的邻接阵

利用MATLAB软件计算得：I1=0.4142，I2=0.3999。通过对以上两个连通图的网络抗毁性计算可以看出，对于相同节点、相同边数，拓扑结构越对称，节点分布越均匀，拓扑结构的抗毁性越强。

4　结束语

健壮性通信网络拓扑结构比较复杂、节点多，全连通图的拓扑结构分布均匀、对称性强，抗毁性在常见网络中最强。本文利用MATLAB软件简化了最短路径的求法，直接输入实际健壮性网络的邻接阵，可以从MATLAB软件中得到结果，从而简化求解抗毁性的步骤。此方法对于复杂网络抗毁性计算简单用时短。非赋权的有向网络和无向网络，都不能利用本文提出的方法求出抗毁性，因此，下一步研究将从网络各节点的赋权和有向性等方面作更深入地考量。

[1]熊小萍.电力系统广域通信网络可靠性分析及优化设计[D].南宁：广西大学,2013.

[2]Douglas R. White and Frank Harary. The cohesiveness of blocks in social networks: node connectivity and conditional density [J].Sociological Methodology,2011,31 (1):305-359.

[3]Douglas R.Shie.Network reliability and algebraic structures[M].New York ：Clarendon Press，1991.

[4]Manchester J. The evolution of transport network survivability [J]. Communications Magazine, IEEE,1990,37 (8):44-5.

[5]罗金龙.城市轨道交通网络复杂性及演化分析[D].北京：北京交通大学,2013.

[6]陈建国.通信网络拓扑结抗毁性评估法研究[J].通信系统与网络技术，2006,32(1):6-8.

[7]郭伟.野战地域通信网可靠性的评价方法[J].电子学报，2000,28(1):3-6.

[8]赵静娴.基于不重叠路径熵的网络抗毁性评估方法[J].计算机应用研究，2015,32(3):825-827.

[9]魏福林.野战地域通信拓扑层抗毁性研究[D].郑州：中国人民解放军信息工程大学，2006.

[10] 饶育萍.基于最短路径数的网络抗毁性评价方法[J].通信学报，2009,30(4):113-116.[11] 周炯磐.通信网理论基础[M].北京：人民邮电出版社，1991：94-96.

[责任编校： 张众]

The Invulnerability of Robust Communication Network

ZHANG Xiaomeng1，2，WEN Changjun1，2

(1SchoolofMechanicalEngin.,HubeiUniv.ofTech.,Wuhan430068,China；2HubeiProvincialKeyLaboratoryofModernManufacturingQualityEngin.,Wuhan430068,China)

Based on the fully connected network and the shortest path for evaluation index, the model of the robust communication network invulnerability is established. A new method of calculation of the shortest path is put forward by using MATLAB in this paper. By means of calculating the examples, the network of the invulnerability can be concluded. At the same time, the more symmetrical the robust communication network topology is, the better the invulnerability is.

invulnerability; topology; the shortest path; robust communication network; MATLAB

2016-03-15

张小萌(1990-)，女，湖北武汉人，湖北工业大学硕士研究生，研究方向为可靠性工程

文昌俊(1970-)，男，湖北仙桃人，湖北工业大学教授，研究方向为质量与可靠性

1003-4684(2016)04-0038-03

TN915.02

A