求解子集问题的鲶鱼效应蝙蝠蚁群优化
2016-10-18刁兴春曹建军许永平
刘 艺, 刁兴春, 曹建军, 丁 鲲, 许永平
(1. 解放军理工大学指挥信息系统学院, 江苏 南京 210007;2. 中国人民解放军总参谋部第六十三研究所, 江苏 南京 210007)
求解子集问题的鲶鱼效应蝙蝠蚁群优化
刘艺1, 刁兴春2, 曹建军2, 丁鲲2, 许永平2
(1. 解放军理工大学指挥信息系统学院, 江苏 南京 210007;2. 中国人民解放军总参谋部第六十三研究所, 江苏 南京 210007)
为求解子集问题,提出一种新的基于图的蚂蚁系统——鲶鱼效应蝙蝠蚁群优化(catfish bat algorithm-ant colony optimization,CBA-ACO)。基于子集问题的构造图,利用路径概率转移公式进行路径搜索,采用等效路径信息素增强进行信息素更新;动态维护一定数量较好路径作为档案信息;使用混沌映射并结合鲶鱼效应对蝙蝠算法(bat algorithm,BA)进行改进,在全局最优解多次未更新时,利用档案信息初始化鲶鱼效应增强搜索,返回较好路径解;采用本轮迭代最优更新和增强搜索更新两种方式更新信息素,兼顾算法的收敛速度和搜索能力。对算法进行了描述并分析算法复杂度。结果表明,CBA-ACO具有更好的稳定性和获取较好解的能力。
基于图的蚂蚁系统; 蝙蝠算法; 鲶鱼效应; 混沌映射
0 引 言
优化是具有普适性的工程数学问题,通俗的说,就是如何寻找到最好的(或理想的)解决方案。背包问题(knapsack problem,KP)是一个具有代表性的求解子集优化问题(无序组合优化问题)[1],它已经应用在诸多领域中,例如项目选择、资金分配优化、材料切割、货物装载等,因此求解背包问题具有重要的理论和实际意义。蚁群优化(ant colony optimization,ACO)是一种应用广泛的元启发式算法,它是受自然界蚁群共同觅食行为的启发,由文献[2]提出的一种启发式算法。该算法具有并行分布式计算、信息正反馈、较强鲁棒性、易于与其他算法结合等优点,近年来在各领域得到了快速发展[3]。它最早被用于解决旅行商问题(有序组合优化问题),取得了较好的效果,随后在其他组合优化问题中也得到了运用,例如背包问题和特征选择等[4]。求解子集问题蚁群算法的基本模型包含3种:第1种是文献[5]提出的将信息素放在物品上,没有路径的概念,因此信息素的更新对蚂蚁行为的影响具有不确定性,文献[6-8]在信息素更新环节作了不同改进,但并未改变将信息素放在物品上这一基本模式;第2种是文献[9]提出的将问题转化成带权图,带权图的边上放置信息素,但该方法没有对问题本身的无序信息进行充分利用;第3种是文献[10]提出了一种基于图的蚂蚁系统(graph-based ant system,GBAS),算法在构造图的基础上,提出了等效路径的概念,将问题的无序信息和有向图的路径联系起来,实现了将无序信息转化为有序信息,算法性能得到有效提升。
蝙蝠算法(bat algorithm,BA)是文献[11]受蝙蝠飞行行为启发在2010年提出的一种新型启发式算法,它结合了和声算法和粒子群算法的优点,可以看作是两种方法的混合算法。BA算法提出以来,已经有多篇研究将其应用在连续函数的优化问题中[12-14],并取得了很好的效果。但是,目前用该算法解决组合优化问题的成果并不多见。
为了求解子集问题,本文提出一种新的基于图的蚂蚁系统——鲶鱼效应蝙蝠蚁群优化(catfish bat algorithm-ant colony optimization, CBA-ACO)。基于子集问题的构造图,采用路径概率转移公式进行路径搜索,利用等效路径对信息素进行增强更新;在迭代过程中,动态维护一定数量较好路径作为档案信息;使用混沌映射并结合鲶鱼效应对BA算法进行改进,在全局最优解多次未更新时,利用档案信息初始化鲶鱼效应增强搜索,返回较好路径解;采用本次迭代最优更新和增强搜索更新两种方式更新信息素,兼顾算法的收敛速度和搜索能力。对采用的鲶鱼效应,鲶鱼效应增强搜索进行实验,并进行参数敏感性分析,验证CBA-ACO的有效性以及在寻优能力和获得解的稳定性上的优越性。
1 相关理论简介
1.1基于图的蚂蚁系统
基于图的蚂蚁系统(graph-based ant system, GBAS)包括以下几个组成部分[10]:
(1) 针对具体问题的构造图:一般包括一个有向图和若干个从有向图到具体问题的映射,构造图实现了问题到有向图表示的映射;
(2) 智能蚁群:每个智能蚂蚁依据所给定的状态转移概率,在有向图中进行依次随机行走,构造满足约束条件的可行解,所有蚂蚁均完成一次行走过程后,一次迭代结束,智能蚂蚁死亡;
(3) 蚂蚁随机移动的状态转移概率:通过有向图边上的信息素量和启发式信息量计算状态转移概率,蚂蚁依据概率信息进行独立的随机行走;
(4) 构造图中有向图边上的信息素量:信息素量随迭代次数变化,一次迭代完成后,按照一定的规则对信息素进行更新;
(5) 构造图中有向图边上的启发式信息:启发式信息代表了蚂蚁选择该条边的期望程度,启发式信息为内部信息,由问题本身的特点决定。
文献[10]提出的GBAS采用了等效路径概念,对包含同一子集解的其他路径同时更新信息素,这就增强了算法求解子集问题的能力。因此,本文使用包含等效路径的GBAS作为求解子集问题的基本算法模型。
1.2BA算法
蝙蝠是一种特别的生物,其中微型蝙蝠使用回声定位来躲避障碍和探测猎物。多数微型蝙蝠使用调频信号,而其他一些则使用固定频率的信号,但是它们原理都是基于回声定位的声学原理。文献[11]受到微型蝙蝠这种回声定位的飞行行为方式启发,于2010年提出了BA算法。BA算法包括信号频率的变化,速度和位置的更新以及响度的变化,而蝙蝠的速度和位置的更新策略与标准粒子群算法(particle swarm optimization,PSO)更新速度和位置的策略有很多相似之处。实质上,PSO与和声搜索都是BA在适当简化下的特殊情况[15],结合了两种方法的优点。本文在算法全局最优解多次未更新的情况下使用BA,在更广阔的空间中寻找较好解,提高算法的全局搜索能力。
1.3鲶鱼效应
鲶鱼效应是指在某个进化群体中,个体的更新处于基本停滞的状态下引入若干性能优越的个体而激活整个群体进化能力的负反馈策略,它最初是由贩卖沙丁鱼的商人通过加入鲶鱼保持其活性的行为而被发现,随后在金融界和企业管理中,管理人员也通过使用鲶鱼效应引入竞争机制,从而提高自身的竞争力。文献[16]将鲶鱼效应与粒子群算法相结合,通过使用具有优秀性能的鲶鱼粒子,改善了算法求解复杂优化问题的能力。本文借鉴鲶鱼效应对BA进行改进,在BA即将陷入局部最优时启动鲶鱼效应,避免过早收敛,提高算法的全局探测能力。
2 CBA-ACO优化
2.1路径搜索和信息素更新
求解子集问题的基于图的蚂蚁系统具体模型如图1所示[10]。
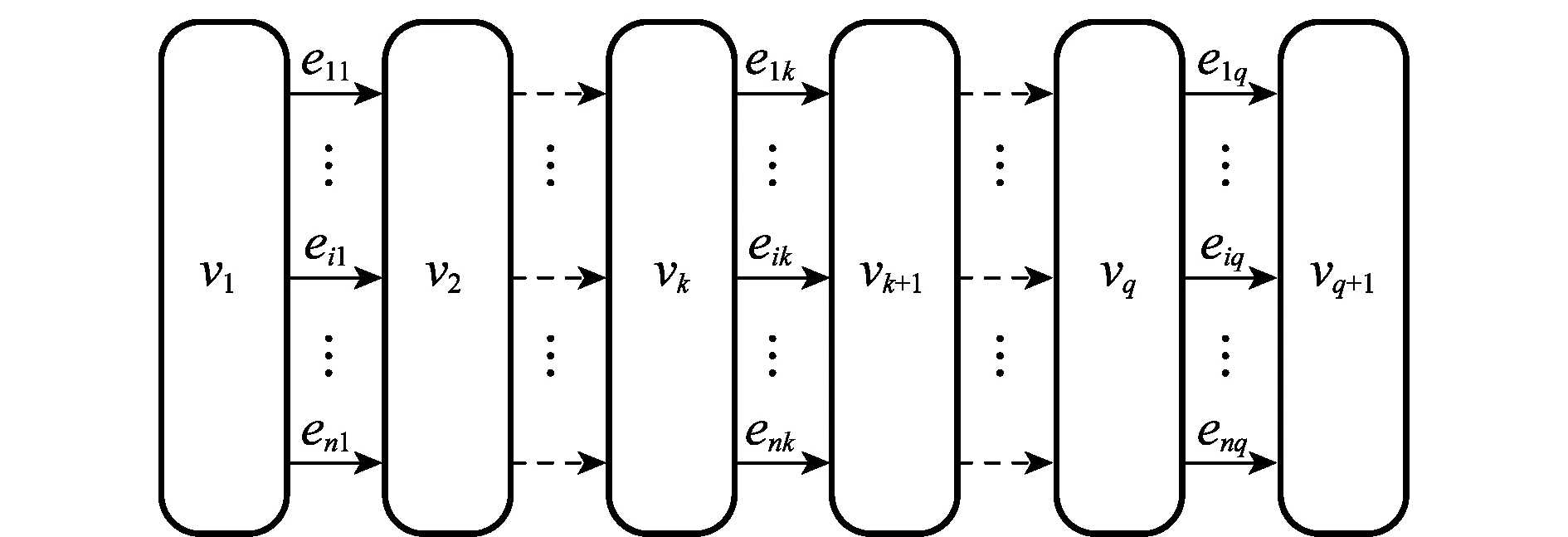
图1 子集问题构造图的有向图Fig.1 Directed graph of subset problem’s structure graph
图1中,n为备选集的基数;q为所求子集的最大可能基数;eij表示在第j步选择第i个元素。
在GBAS中使用的路径概率转移公式为[8]
(1)
式中,禁忌表tabum(m=1,2,…,M)记录第m只蚂蚁走过的边;α和β分别为信息素量和启发式因子的重要程度;τij为当前时刻边eij上的信息素量;ηi是启发式因子,表示选择第i个元素的期望程度,表达式视具体问题而定。
一次迭代完成后,拟对等效路径上的信息素增强,信息素更新公式[10]为
(2)
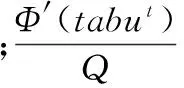
2.2交互机制
为了提高GBAS求解子集问题的性能,在GBAS的全局最优解多次未更新的情况下,启动鲶鱼效应增强搜索提高算法收敛到全局最优的概率。在此过程中,需要将GBAS的当前信息传递给鲶鱼效应增强搜索,在增强搜索结束后,也需要将结果返回给蚁群算法,因此GBAS和增强搜索的交互分为两个阶段:信息传递和结果返回。
(1) 信息传递
鲶鱼效应增强搜索中,一个重要的阶段是蝙蝠种群的初始化,它决定了增强搜索算法的初始状态和搜索能力,因此优秀的蝙蝠初始种群对算法的性能及运行结果至关重要。本文采用GBAS更新中动态选取蚂蚁搜索出的一定数量的较好路径作为档案,档案规模取1~2倍的蚂蚁数,使个体具有一定多样性又不使档案规模过大。启动鲶鱼效应增强搜索时,将档案信息作为参数初始化蝙蝠种群进行搜索。
(2) 结果返回
为了提高算法的运行效率,除了设定增强搜索算法迭代次数上限,GBAS也要将当前全局最优值作为参数同时传递给增强搜索,当增强搜索发现比蚁群算法的当前全局最优解更好的路径时即停止搜索返回结果。
2.3鲶鱼效应增强搜索
本节提出使用混沌搜索且具有鲶鱼效应的BA对GBAS的性能进行提升,使得算法具有更强的全局搜索能力。
2.3.1频率变化区间混沌搜索
在基本的BA算法中,每只蝙蝠个体利用自身的回声定位系统,计算出自身与群体当前最优解之间的距离,通过使用脉冲频率来调节自己在下一代运行时的速度, 在t+1时刻蝙蝠的位置和速度更新公式[11]如下:
(3)
(4)
(5)
式中,Fi表示蝙蝠i在当前时刻发出的声波脉冲频率;Fmax,Fmin分别表示脉冲频率的最大值和最小值;β∈[0,1]是一个服从均匀分布的随机向量;式(4)中的x*表示当前全局最优位置(解)。
然而从[Fmin,Fmax]随机生成的脉冲频率可能使得蝙蝠的速度变化局限在某个区间段内。观察式(5)可以看出,当蝙蝠个体的搜索范围靠近当前最优解时,其速度的变化会逐渐趋于零,从而影响了蝙蝠的搜索能力。同时,蝙蝠的脉冲信号发射速率的提升也使得其在邻域内搜索到更好解的能力下降,这就使得算法易陷入局部最优,增加蝙蝠群体搜寻的最终解与初始值的关联性。

(6)
(7)
2.3.2算法描述
与多数群智能算法类似,在BA算法执行过程中,如果最优解和周围蝙蝠的距离很小,那么每只蝙蝠就会成为围绕在最优解附近簇的一部分,在下一次迭代过程中,只能移动很小的距离。此时算法就陷入了局部最优。为了避免这种情况,当BA算法陷入停滞,过早收敛时,可以引入“鲶鱼”蝙蝠来刺激其他“沙丁鱼”蝙蝠进行新的搜索。在算法具体执行过程中,通过使用“鲶鱼”蝙蝠来代替当前蝙蝠种群中适应度值最差的10%个体。
此外,在算法中,蝙蝠的局部搜索过程[11]为
(8)
式中,ε∈[-1,1]是一个随机数;At是所有蝙蝠在同一个时间段的平均音量。
音量和脉冲发射率的迭代更新公式[11]为
(9)
式中,α和γ为常量。结合第2.2.1节对BA的混沌搜索改进,鲶鱼效应增强搜索的伪代码如下:
Begin
接受档案信息和GBAS当前全局最优解,初始化蝙蝠种群;
WHILE(增强搜索算法全局最优解小于GBAS当前全局最优解或者未达到最大迭代次数)
FORi=1∶AN
利用式(6)更新混沌值;
采用式(7)、式(4)、式(5)产生新解;
IF 脉冲发射率小于随机产生的随机数
采用式(8)得到一个局部解;
END IF
利用评价函数计算个体适应度值;
IF 音量大于随机产生的随机数且新的个体适应度小于当前个体适应度
接受该解作为当前个体最新解;
更新当前蝙蝠个体最优值;
通过式(9)更新音量和脉冲发生率;
END IF
更新增强搜索算法的当前全局最优解及其对应参数;
IF 增强搜索算法的当前全局最优解大于G次未更新
对蝙蝠种群按照适应度值从最差到最好排列;
选择最差的10%蝙蝠个体,随机选择当前蝙蝠种群中的最大最小极值点对蝙蝠个体的解向量进行替换,并将速度置为0;
END IF
END FOR
END WHILE
End
鲶鱼效应增强搜索伪代码中的WHILE判定为算法运行的结束条件,通常在启发式算法中,算法运行的结束条件有两种:一种是设定算法运行迭代次数的上限;另一种是设定算法评估函数的结果需要达到的精度。本文选择第一种方式来设定结束条件。同时,为了兼顾算法运行效率,当增强搜索发现比蚁群算法的当前全局最优解更好的路径时即停止搜索返回结果。
2.4信息素更新策略
为兼顾算法收敛速度和全局搜索能力,分两种情况更新信息素矩阵。
(1) 本次迭代最优更新
若本次迭代最优解好于当前全局最优解或者全局最优解小于G次未更新,则对本次迭代最优路径tabut,由式(2)进行信息素矩阵更新。
(2) 增强搜索更新
若全局最优解大于G次未更新,则启动鲶鱼效应增强搜索,将档案信息以及当前全局最优值传递给搜索算法,算法运行结束后返回路径tabut,由式(2)进行信息素矩阵更新。需要特别说明的是,如果增强搜索在到达迭代次数上限结束搜索后,仍未发现较好路径,则算法依然返回搜索的最终结果,这样可以增加信息素更新的多样性,增强蚁群优化算法的全局搜索能力。
2.5算法描述
在GBAS基础上,在算法主体迭代中最优解更新出现停滞的情况下,启动鲶鱼效应增强搜索对更广阔的问题空间进行搜索,寻找较好的路径,利用较好解对等效路径上的信息素更新,使得蚂蚁在下次迭代中以较大概率选择较好路径,提高算法的全局探测能力。
GBAS是用来解决组合优化问题,而组合优化是一种离散优化问题,需要对应用在连续优化领域中的BA算法进行离散化,离散方法采用文献[17]提出的策略。综上,本文提出的CBA-ACO的伪代码如下:
Begin
初始化
WHILE(未达到最大迭代次数)
生成M只蚂蚁并初始化规模为AN的档案记录;
FORa=1∶M
蚂蚁根据路径上的信息素利用式(1)寻找最优解;
更新本次迭代最优解;
动态刷新档案记录
END FOR
IF 本次迭代最优解好于当前全局最优解或全局最优解小于G次未更新
更新全局最优解并利用式(2)更新信息素;
ELSE 传递档案信息以及GBAS的当前全局最优解,并运行鲶鱼效应增强搜索,输出算法运行最优解;
更新全局最优解并利用式(2)更新信息素;
END IF
输出最优结果
END WHILE
End
2.6算法复杂度分析
在鲶鱼效应增强搜索中,蝙蝠寻找最优解上的时间复杂度(最坏情况)为O(NC×N),其中NC为BA算法最大迭代次数,N为蝙蝠种群规模;运行鲶鱼效应的时间复杂度为O(NC×nN),其中n为备选集的基数,因此鲶鱼效应增强搜索在最坏情况下的时间复杂度为O(NC×nN)。
在CBA-ACO中,蚂蚁搜索可行路径的时间复杂度为O(MC×n2),其中MC为算法最大迭代次数,n为备选集的基数;CBA-ACO运行鲶鱼效应增强搜索的时间复杂度为O(MC×NC×nN),这部分是CBA-ACO程序中耗时最长的计算步骤,因此CBA-ACO在最坏情况下的时间复杂度为O(MC×NC×nN)。
鲶鱼效应增强搜索的空间复杂度为O(N×n),蚁群算法中信息素表是占用存储资源最大的部分,空间复杂度为O(n2),因此CBA-ACO的空间复杂度为O(n2+N×n)。
3 实验结果与分析
3.1CBA-ACO实验分析
为了验证CBA-ACO优化的有效性和优越性,以多维背包问题为例,对算法进行仿真和测试。同时,将不包含鲶鱼效应增强搜索的CBA-ACO(算法1)和包含增强搜索但未加鲶鱼效应的CBA-ACO(算法2)与本文提出的完整CBA-ACO优化(算法3)进行对比实验。
多维背包问题(multidimensional knapsack problem, MKP)的形式化表示为
(10)
(11)
式中,n为物品的个数;pi为第i个物品的价值;cbi(b=1,2,…,r)为第i个物品第b个约束向量;r为问题的维数;xi(i=1,2,…,n)为解向量。r维背包问题可以表述为,在具有r个约束的条件下,从n个物品(候选解)中选择一组物品(子集),使背包所含物品的价值最大。
测试实例来自网站:http:∥elib.zib.de/pub/Packages/mp-testdata/ip/sac94-suite/index.html。
实例 1weish06.dat,背包个数为5,背包维度为40,最优解为5 557。
(1) 算法1参数设置[10]如下:α=0.8,β=0.2,ρ=0.2,τij(0)=100,M=20,Q=200。
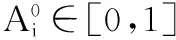
(3) 算法3参数设置如下:鲶鱼效应启动条件g=10,其他与算法2一致。
实例 2weish14.dat,背包个数为5,背包维度为60,最优解为6 954。
(1) 算法1参数设置[10]如下:α=1,β=0.2,ρ=0.2,τij(0)=100,M=20,Q=300。
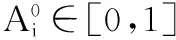
(3) 算法3参数设置如下:鲶鱼效应启动条件g=10,其他与算法2一致;
实例 3weish28.dat,背包个数为5,背包维度为90,最优解为9 492。
(1) 算法1参数设置[10]如下:α=1.2,β=0.2,ρ=0.2,τij(0)=100,M=20,Q=300。
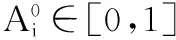
(3) 算法3参数设置如下:鲶鱼效应启动条件g=10,其他与算法2一致。
测试过程中对算法的迭代次数取MC=[10∶10∶200],每个实例各运行20次,计算所得解的均值和方差,测试结果如图2~图7所示,并将算法发现所提供最优解的次数列于表1~表3(部分)。

图2 实例1解的均值Fig.2 Mean value of solutions of instance 1
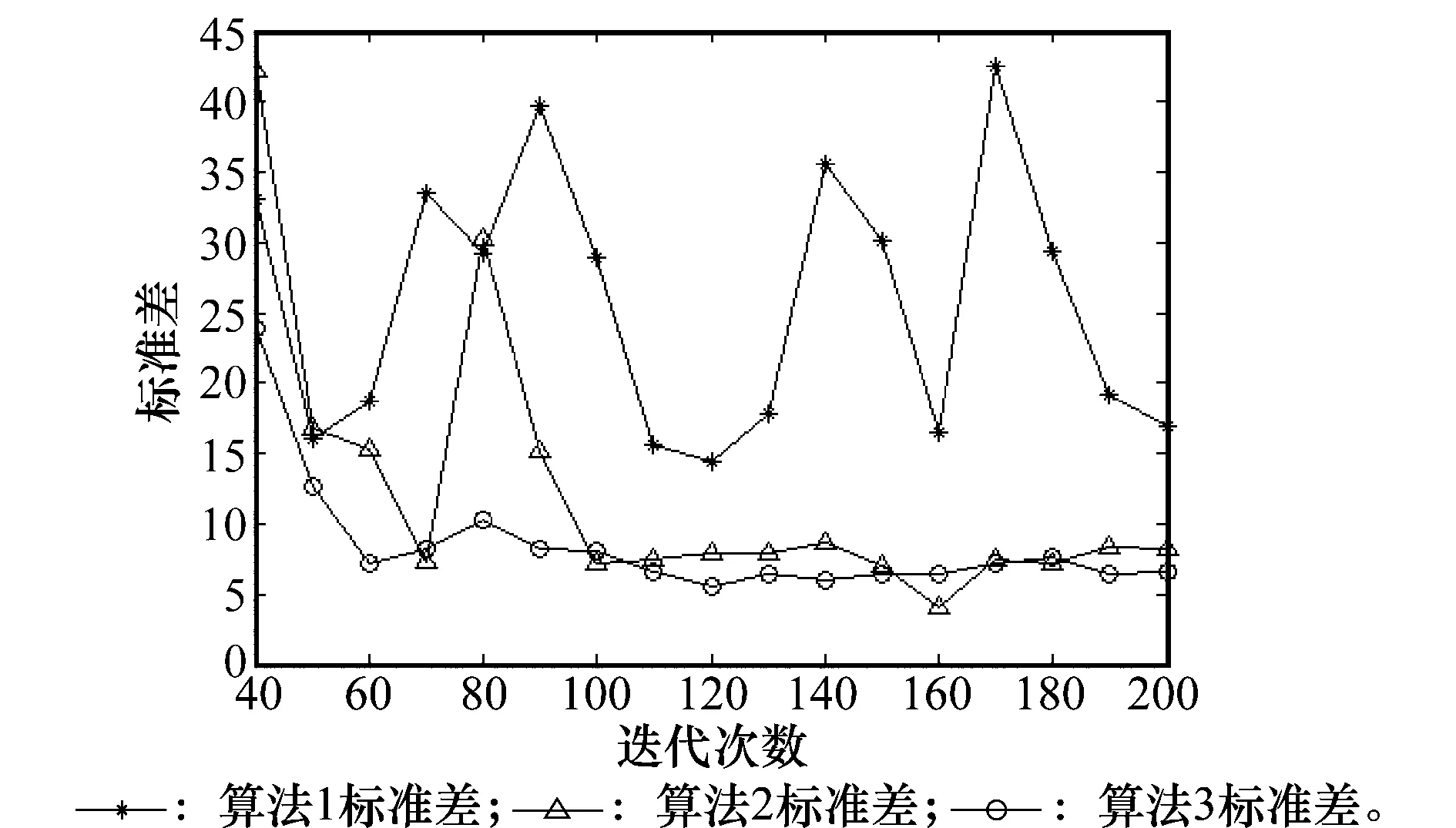
图3 实例1解的标准差Fig.3 Standard deviation of solutions of instance 1
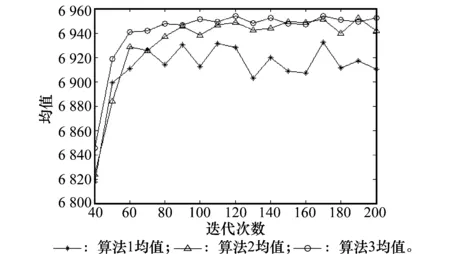
图4 实例2解的均值Fig.4 Mean value of solutions of instance 2
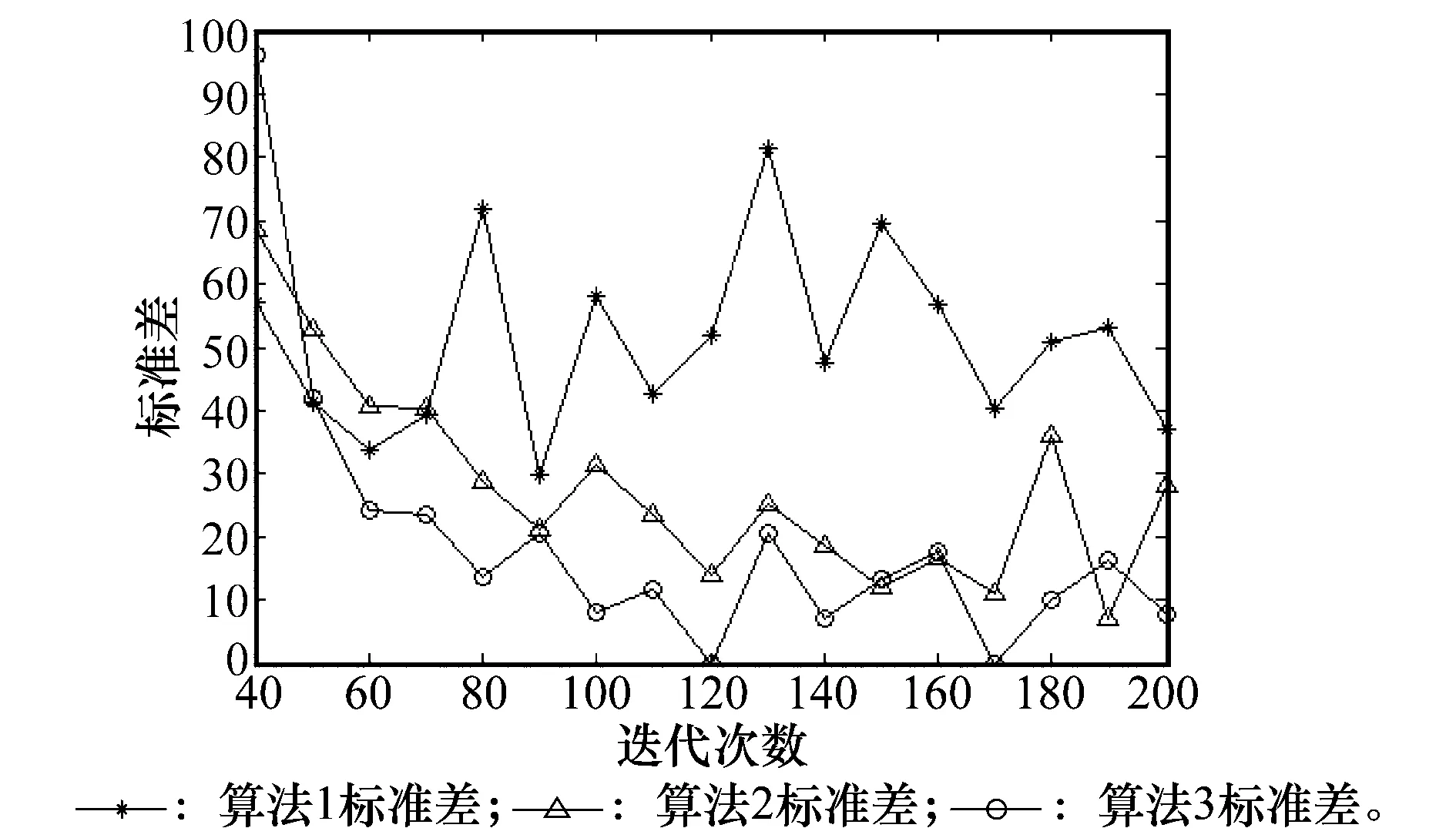
图5 实例2解的标准差Fig.5 Standard deviation of solutions of instance 2
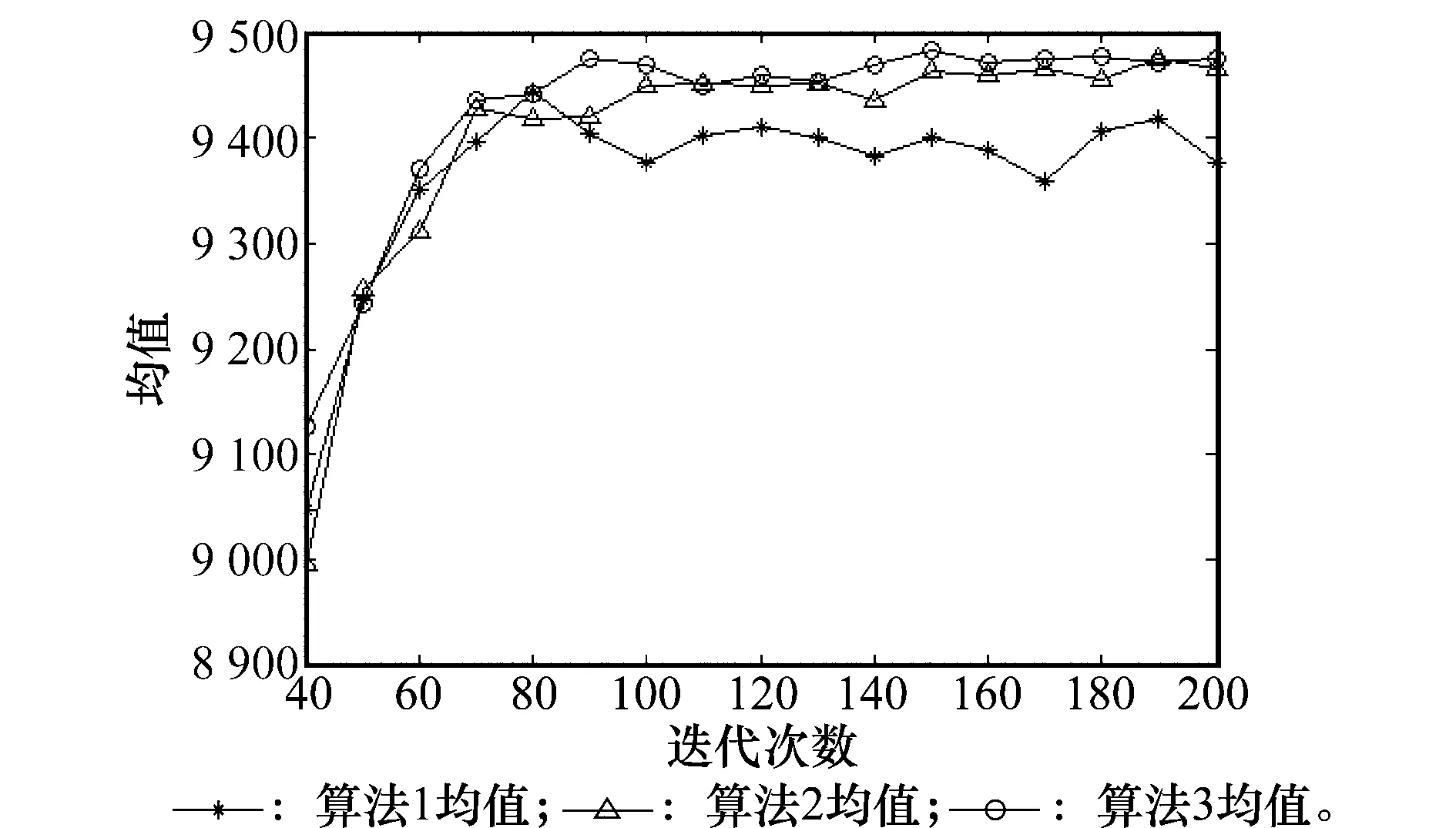
图6 实例3解的均值Fig.6 Mean value of solutions of instance 3
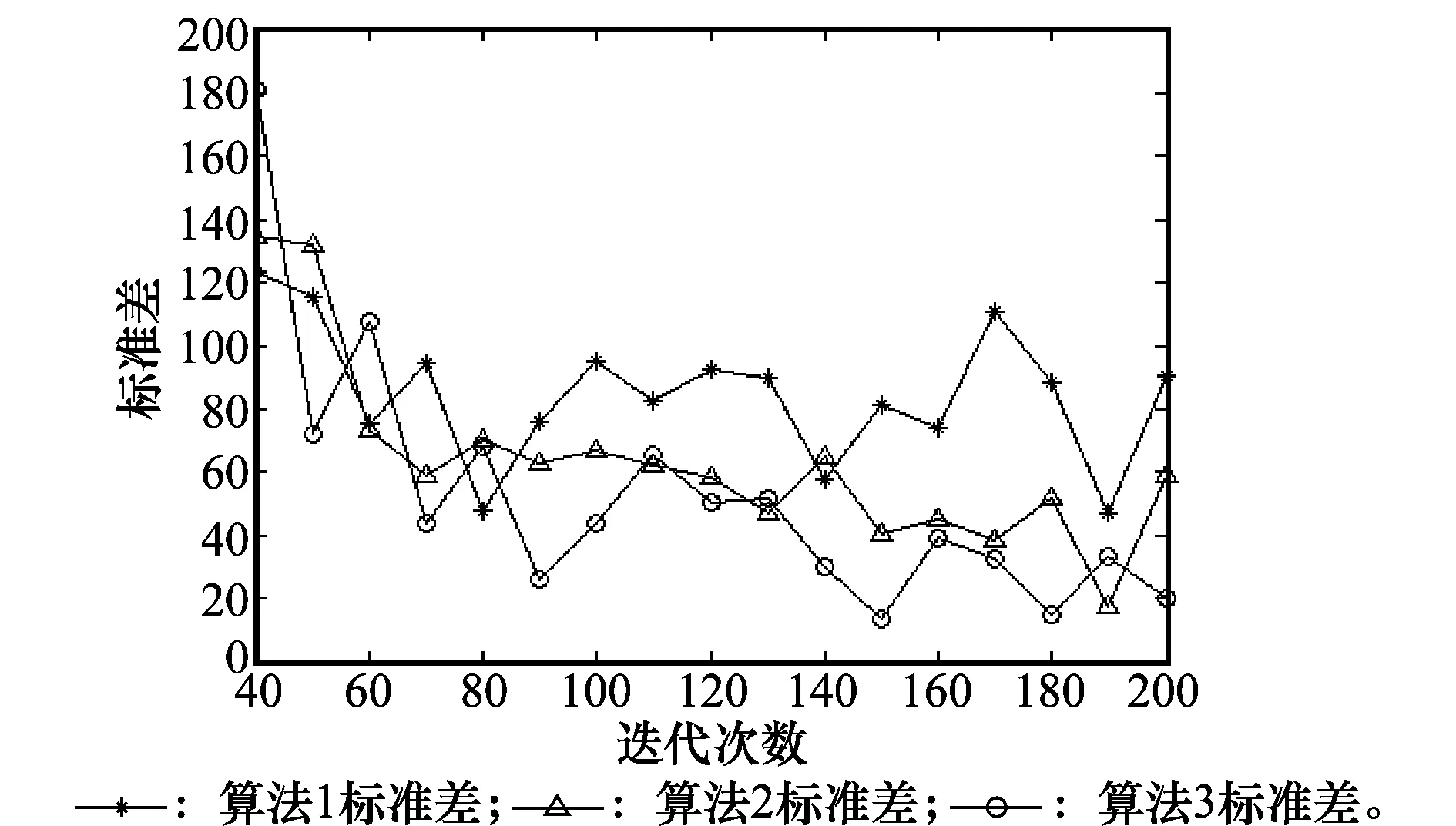
图7 实例3解的标准差Fig.7 Standard deviation of solutions of instance 3
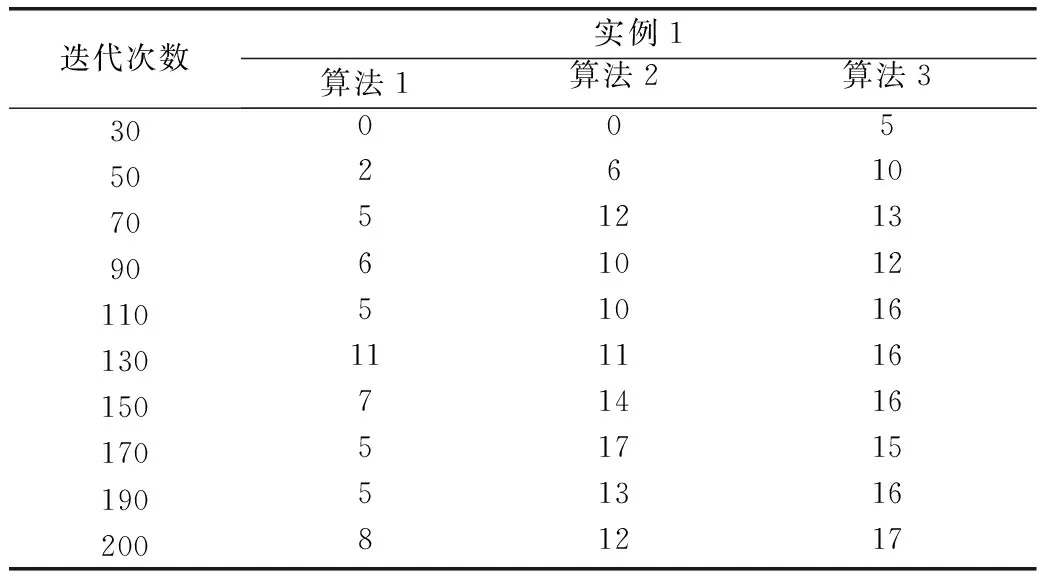
迭代次数实例1算法1算法2算法330005502610705121390610121105101613011111615071416170517151905131620081217
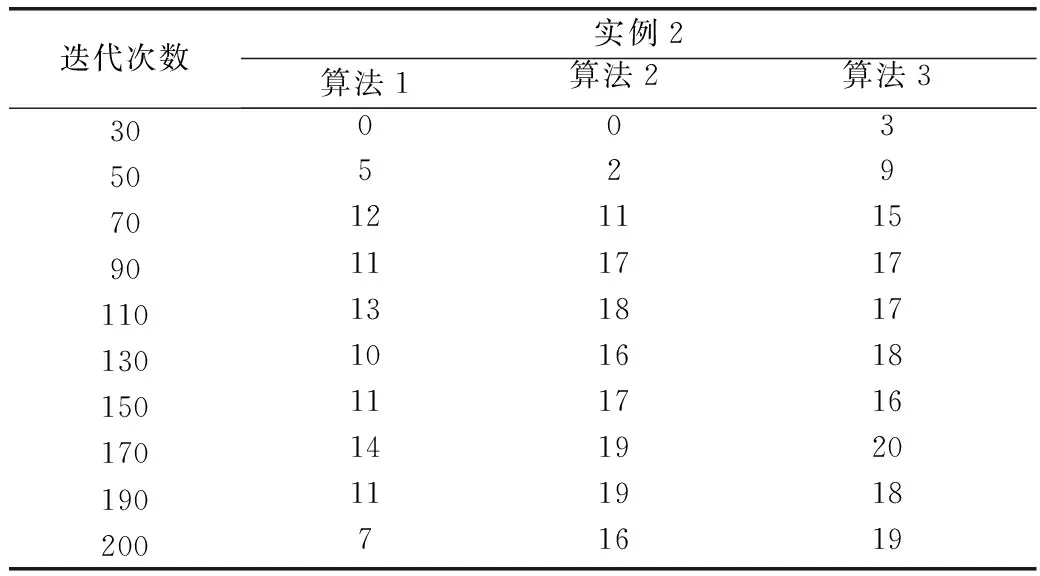
表2 实例2发现所提供最优解的次数
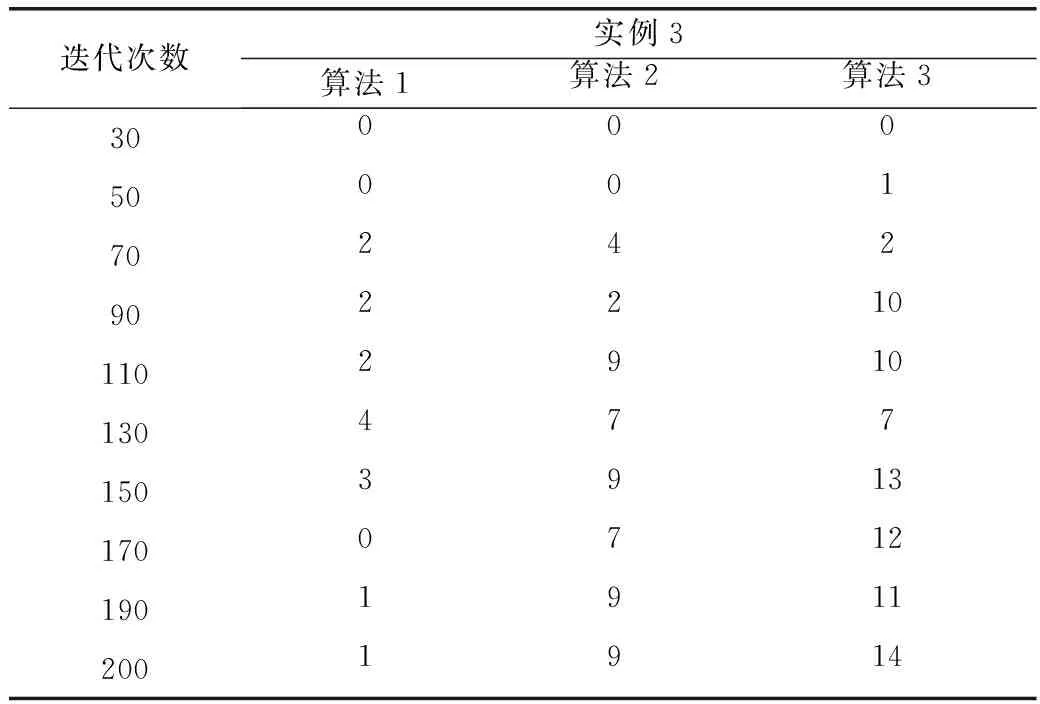
表3 实例3发现所提供最优解的次数
首先分析测试实例中的均值。通过对比图2、图4和图6中的均值能够发现,在实例2和实例3的测试条件下,算法2和算法3都要好于算法1,这是由于在GBAS的全局最优解多次未更新的情况下,启动了增强搜索,由于不受算法中信息素的限制,使得增强搜索能够在更广阔的搜索空间中寻找更好的最优解,再使用等效路径进行信息素更新,提高了算法的全局探测能力,验证了增强搜索具有提高算法全局搜索性能的能力。但是,在实例1的测试条件下,算法2的均值与算法1相比没有明显的提高,算法3的均值与算法2和算法1相比具有明显的优势,这是因为算法2在蝙蝠寻优的过程中会陷入局部最优,导致寻找的结果不稳定,在这种情况下具有鲶鱼效应的算法3就能够跳出局部最优值,这就使得算法3算法能够以较大的概率发现比算法2更好的最优解,这也验证了鲶鱼效应具有解决过早收敛问题的能力。
对比图3、图5和图7中的标准差,能够发现在实例2和实例3的测试条件下,算法2和算法3都要好于算法1,这是由于在GBAS全局最优解多次未更新的情况下,启动了增强搜索寻找到更好的最优解并进行信息素更新,提高了算法获得较好解的能力。而在实例1的测试条件下,算法3比算法2和算法1具有更小的标准差,算法2与算法1相比在标准差的比较中并没有明显的优势,这是由于BA算法陷入局部最优,产生过早收敛问题,导致寻优结果不稳定。而包含鲶鱼效应的算法3则很好的解决了该问题。
观察表1~表3提供的最优解出现次数,算法2与算法1相比,能够提供更多次最优解,而算法3的优势要比算法2更为明显,这是由于算法3包含解决过早收敛问题的鲶鱼效应,使得算法3拥有更强的全局搜索能力,增加了发现最优解的概率。
同时,为了验证算法的运行耗时,记录下3个算法的运行时间,并以算法1作为基准,对运行时间作归一化处理,得到的结果如表4所示。
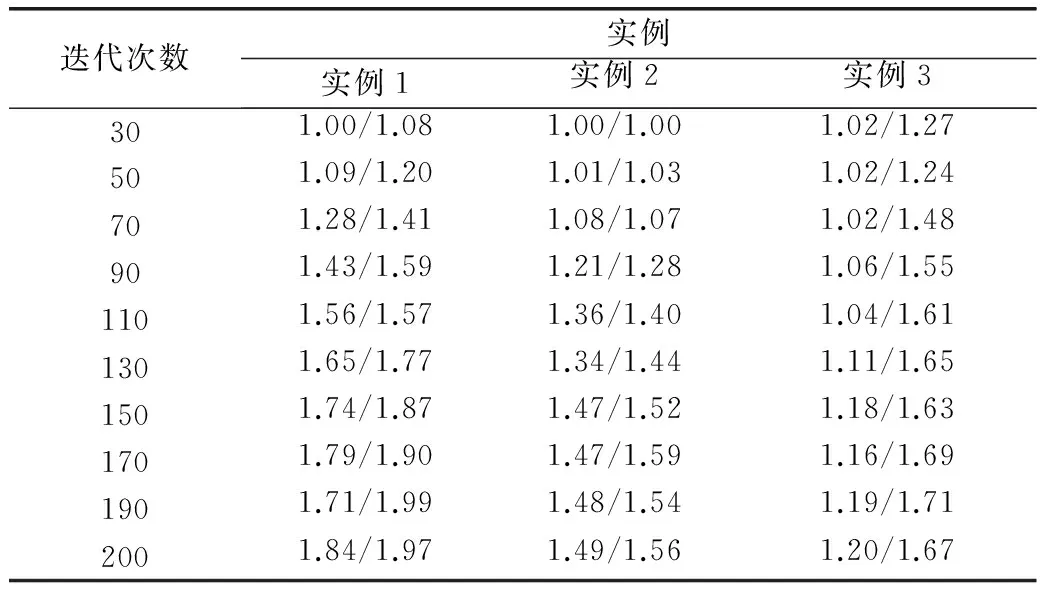
表4 算法2和算法3的相对运行时间
从表4中观察可以看出,算法3和算法2的运行时间随着迭代次数的增加而增加,算法3由于增加了鲶鱼效应,因此在时间上要比算法2更加耗时。算法3和算法2的运行时间都没有超过算法1运行时间的2倍,这是由于在增强搜索中除了设定运行次数的上限,还将发现当前全局最优解作为停止的条件,一旦发现比当前全局最优解更好的解时,算法2和算法3都停止运行,返回发现的更好解,有效降低了运行时间。
综上,鲶鱼效应增强搜索对提高算法的寻优和收敛能力具有有效性。同时表明包含鲶鱼效应增强搜索的CBA-ACO具有更强的发现较好解的能力,解的稳定性也较好,是一种很好的混合启发式方法。
3.2CBA-ACO参数敏感性分析
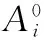
分析过程中G和g的取值均为[1 3 5 7 9 11 13 20],对算法的迭代次数取MC=80,在一次实验中,对设定的G和g值,算法运行20次,计算所得解的均值和方差以及运行时间。其中一次的测试结果如表5和表6所示。
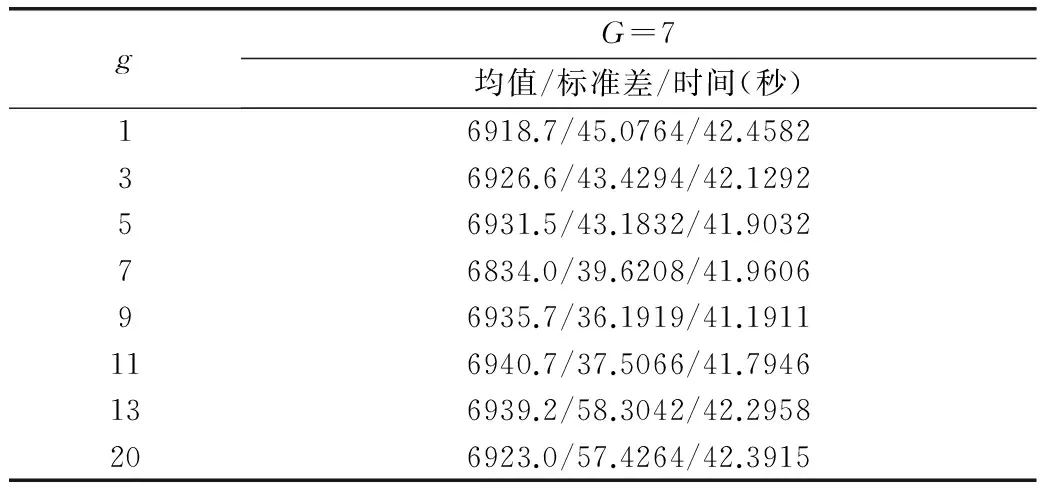
表5 G=7时不同g的运行结果

表6 g=11时不同G的运行结果
从表5中可以看出,在G=7时,不同的g值条件下,算法运行的均值、标准差和运行时间是呈现一定变化趋势的。这是由于当g较小时,鲶鱼效应启动次数较多,造成算法的收敛能力下降,导致均值降低并增大了标准差,而较差的全局最优值也会使得增强搜索的次数增加,提高了算法运行时间;随着g的增加,算法的收敛能力也趋于增强,运行结果也逐渐变好;当g增加到一定程度之后,鲶鱼效应启动次数减少甚至不会启动,这就减小了鲶鱼效应对算法的增强作用,使得算法获取较好解的能力下降,导致运行结果变差,使得增强搜索的运行次数再次增加,提高了算法的运行时间。在其他的G值条件下测试能够得到相同的结论。通过实验分析,g取值在7~11之间时,算法运行结果较好。
分析表6,在g=11时,G值不同,算法的均值、标准差也有所不同。当G较小时,鲶鱼效应增强搜索运行次数较多,导致算法的全局搜索能力下降,均值降低,标准差增加;随着G值逐渐趋近较好范围,算法的全局搜索能力和局部开采能力达到较好的结合状态,算法的运行结果也较好;进一步增加G值时,算法的增强搜索启动次数减少,局部开采能力逐渐减弱,导致均值和标准差呈现较差趋势;分析算法的运行时间,可以看出,算法运行时间对G值的变化并不敏感,这也验证了鲶鱼效应增强搜索的优越性。在其他的g值条件下测试能够得到相同的结论。通过实验分析,G取值在5~9之间时,算法运行结果较好。
4 结 论
为了求解子集问题,提出一种基于图的蚂蚁系统CBA-ACO。
针对BA算法过早收敛的问题,采用混沌映射对频率搜索区间进行改进,一定程度上改善了BA的搜索能力;通过引入鲶鱼效应,使得BA算法能够跳出陷入局部最优的情况,进一步增强了BA算法全局搜索能力。
将改进后的鲶鱼效应增强搜索加入GBAS中,在全局最优解多次未更新的情况下,通过保存较好路径的档案信息初始化并启动增强搜索寻找更好的最优解,提高了算法的全局探测能力。对采用的鲶鱼效应和增强搜索进行实验,并对参数敏感性进行了分析,结果表明了改进的有效性,同时验证了本文提出CBA-ACO具有更好的稳定性和获取较好解的能力。
[1] Ishibuchi H, Akedo N, Nojima Y. Behavior of multiobjective evolutionary algorithms on many-objective knapsack problems[J].IEEETrans.onEvolutionaryComputation, 2015, 19(2): 264-283.
[2] Colorni A, Dorigo M, Maniezzo V. Distributed optimization by ant colonies[C]∥Proc.oftheFirstEuropeanConferenceonArtificialLife, 1991: 134-142.
[3] Liao T J, Socha K, A. Montes de Oca M, et al. Ant colony optimization for mixed-variable optimization problems[J].IEEETrans.onEvolutionaryComputation, 2014, 18(4): 503-518.
[4] Forsati R, Moayedikia A, Jensen R, et al. Enriched ant colony optimization and its application in feature selection[J].Neurocomputing, 2014, 142: 354-371.
[5] Leguizamon G, Michalewicz Z. A new version of ant system for subset problems[C]∥Proc.oftheCongressonEvolutionaryComputation, 1999: 1459-1464.
[6] Parra-Hernandez R, Dimopoulos N. On the performance of the ant colony system for solving the multidimensional knapsack problem[C]∥Proc.oftheIEEEPacificRimConferenceonCommunications,ComputersandsignalProcessing, 2003: 338-341.
[7] Shi H X. Solution to 0/1 knapsack problem based on improved ant colony algorithm[C]∥Proc.oftheIEEEInternationalConferenceonInformationAcquisition, 2006: 1062-1066.
[8] Wang H Y, Jia R Y, Zhang Y G, et al. A quick ant colony algorithm of solving 0-1 knapsack problem[J].ComputerTechnologyandDevelopment,2007,17(1):104-107.(王会颖,贾瑞玉,章义刚,等.一种求解0-1背包问题的快速蚁群算法[J].计算机技术与发展,2007,17(1):104-107.)
[9] Hu X B, Huang X Y. Solving 0-1 knapsack problem based on ant colony optimization algorithm[J].JournalofSystemsEngineering, 2005, 20(5): 520-523.(胡小兵,黄席樾.基于蚁群优化算法的0-1背包问题求解[J].系统工程学报,2005,20(5):520-523.)
[10] Cao J J, Zhang P L, Wang Y X, et al. A graph-based ant system for subset problems[J].JournalofSystemSimulation, 2008, 20(22): 6146-6150.(曹建军, 张培林, 王艳霞, 等. 一种求解子集问题的基于图的蚂蚁系统[J].系统仿真学报, 2008, 20(22): 6146-6150.)
[11] Carlos C, Gonzalez J R,Natalio K, et al.NatureInspiredcooperativestrategiesforoptimization[M]. Yang X S.Anewmetaheuristicbat-inspiredalgorithm.Granada: Springer, 2010: 64-74.
[12] Yang X S.Bat algorithm for multi-objective optimization[J].InternationalJournalofBio-inspiredComputation,2011,3(5):267-274.
[13] Yang X S, Gandomi A H. Bat algorithm: a novel approach for global engineering optimization[J].EngineeringComputation, 2012, 29(5): 267-289.
[14] Gandomi A H, Yang X S, Alavi A H, et al. Bat algorithm for constrained optimization tasks[J].NeuralComputingandApplication, 2013, 22(6): 1239-1255.
[15] Zhao Y X, Yang X S, Liu L Q.Newlydevelopingmetaheuristicoptimizationmethods[M]. Beijing: Science Press, 2013.(赵玉新, 杨新社, 刘利强. 新兴元启发式优化方法[M]. 北京:科学出版社, 2013.)
[16] Chuang L Y, Tsai S W, Yang C H. Chaotic catfish particle swarm optimization for solving global numerical optimization problems[J].AppliedMathematicsandComputation, 2011, 217(16): 6900-6916.
[17] Mirjalili S, Mirjalili S M, Yang X S. Binary bat algorithm[J].NeuralComputingandApplications, 2014, 25(3): 663-681.
曹建军(1975-),通信作者,男,工程师,博士,主要研究方向为进化算法、数据质量控制与数据治理。
E-mail:jianjuncao@yeah.net
丁鲲(1978-),男,高级工程师,硕士,主要研究方向为网络管理。
E-mail:njdingkun@163.com
许永平(1979-),男,工程师,博士,主要研究方向为数据质量控制与数据治理。
E-mail:zuisanlang@163.com
Catfish bat algorithm-ant colony optimization for subset problems
LIU Yi1, DIAO Xing-chun2, CAO Jian-jun2, DING Kun2, XU Yong-ping2
(1. College of Command Information Systems, PLA University of Science and Technology, Nanjing 210007, China;2.The63rdResearchInstituteofPLAGeneralStaffHeadquarters,Nanjing210007,China)
In order to resolve subset problems, a new graph-based ant system called catfish bat algorithm-ant colony optimization (CBA-ACO) is proposed. Based on the subset problem’s structure graph, routes’ probability transition equation is used to search for solutions, equivalent routes’ pheromones strengthening is adopted to update pheromone. Some solutions are maintained in archive dynamically. The chaotic map and catfish effect are adopted to improve the bat algorithm (BA) for the enhanced exploration which is initialized by archive information and used to find better solution in case the global optimal solution is not updated after several runs. After one cycle, the best route of this cycle updating and the enhanced exploration updating are two cases of updating pheromone. As a result the convergence speed and searching capability of the algorithm are improved. The algorithm is described, and its complexity is analyzed. Experiments show that the CBA-ACO algorithm has a better stability and capability for obtaining the optimal solution.
graph-based ant system; bat algorithm; catfish effect; chaotic map
2015-11-23;
2016-06-20;网络优先出版日期:2016-07-20。
国家自然科学基金(61371196);中国博士后科学基金特别资助项目(201003797);解放军理工大学预研基金(20110604,41150301)资助课题
TP 301.6
A
10.3969/j.issn.1001-506X.2016.10.31
刘艺(1990-),男,博士研究生,主要研究方向为数据质量、进化算法。
E-mail:albertliu20th@sohu.com
刁兴春(1964-),男,研究员,硕士,主要研究方向为数据工程。
E-mail:diaoxch640222@163.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160720.1114.002.html
