逼近非合作目标的自适应二阶终端滑模控制

2016-10-18刘海龙史小平毕显婷

系统工程与电子技术 2016年10期

关键词：滑模航天器姿态

刘海龙, 史小平, 张　杰, 毕显婷

(哈尔滨工业大学控制与仿真中心, 黑龙江哈尔滨 150001)

逼近非合作目标的自适应二阶终端滑模控制

刘海龙, 史小平, 张杰, 毕显婷

(哈尔滨工业大学控制与仿真中心, 黑龙江哈尔滨 150001)

针对逼近非合作目标过程中的相对轨道姿态耦合控制问题,综合考虑系统不确定性、外部干扰以及滑模控制中的抖颤问题,设计了无抖颤的自适应二阶非奇异终端滑模(secondordernonsingularterminalslidingmode,SONTSM)控制器。首先根据视线坐标系下的相对运动方程和体坐标系下的相对姿态方程建立了相对位置和姿态一体化模型。将高阶滑模控制思想与非奇异终端滑模控制理论相结合,使所设计控制器克服了传统滑模的抖颤问题,并同时具有收敛快、精度高、鲁棒性强及能量消耗小等优势。基于Lyapunov理论,对系统稳定性进行了严格的证明。数值仿真验证了控制器的正确性和良好的控制性能。

非合作目标; 相对运动; 终端滑模; 耦合控制; 二阶滑模控制

0　引　言

随着空间科学技术的发展和深入,空间应用经历了由单星系统到多星系统,由传统对合作目标的交会任务到对非合作目标的逼近、抓捕等新的研究和实践过程。对非合作目标的研究有着广泛的应用前景,如在轨服务技术、空间碎片捕获及空间攻防等,因此对非合作目标的研究受到了国内外学者的广泛关注。

与传统合作目标相比,对非合作目标的控制有着很大不同[1],具体包括:①目标航天器运动状态及轨道参数等信息未知,仅能通过敏感器测量获得其运动状态或相对运动状态;②由于目标航天器常处于失控状态或存在机动,加之追踪航天器存在严重的姿轨耦合问题及挠性附件对系统稳定的影响,故考虑姿轨耦合及挠性附件影响下的高精度控制成为了当前研究的热点问题;③由于相对运动状态仅能通过测量获得,故系统状态的获得存在延时问题[2]的影响。

当前,国内外学者主要针对处于自由翻滚状态的非合作目标展开研究,文献[3]基于模型预测控制对航天器间的相对运动进行了研究,考虑到航天器在交会阶段和对接阶段具有不同的约束、要求和采样速率,设计了具有动态可重构约束的模型预测控制器。文献[4-5]在建立六自由度耦合动力学模型时考虑了姿轨耦合因素对系统的影响,在此基础上,通过设计自适应律估计了系统的参数不确定性,并基于传统线性滑模控制方法设计了姿轨一体化控制器。文献[6-7]基于终端滑模控制理论与有限时间干扰观测器技术,提出一种利用终端滑模控制进行反馈控制,并结合有限时间干扰观测器对干扰进行前馈补偿的控制策略,由于控制器中符号函数的幅值仅需大于干扰估计误差,从而一定程度上削弱了抖颤现象的影响。文献[8]针对姿轨耦合问题,将超扭曲算法与自适应方法相结合,设计了具有变增益的自适应超扭曲控制器,进一步提高了系统的鲁棒性及减弱抖颤现象的影响。文献[9]在建立类拉格朗日形式姿轨耦合动力学模型的基础上,将线性滑模和自适应技术相结合设计了控制律,所设计控制律具有一定的抗饱和能力以及不依赖于目标航天器动力学参数的优势。文献[10]在视线坐标系下得到了相对轨道动力学方程,设计了具有较强实时性的姿轨耦合θ-D控制器,进一步考虑了目标航天器可能存在机动的情况,基于Lyapunov最小-最大定理对控制器进行了修正。文献[11]在对非合作目标姿轨耦合控制问题的建模与控制律设计中,考虑了挠性附件对系统的影响。文献[12]基于Hill坐标系建立了航天器姿轨耦合动力学模型,在考虑控制输入耦合对系统影响的基础上,进一步基于反馈线性化方法得到了姿轨耦合控制器,此外,对航天器的姿轨耦合源进行了较深入的分析。

然而,多数文献在对航天器姿轨耦合问题进行建模时均假设目标航天器的轨道参数已知,且相对运动方程多建立在轨道坐标系之上,这种建模方法的缺点在于其实际工程应用通常依赖于高精度的相对导航算法,且当目标轨道参数未知时将不再适用。

针对在实际工程应用中存在非合作目标运行参数难以测算以及敏感器安装等问题,有学者对传统相对轨道动力学模型进行改进,提出了基于视线坐标系的建模方法[10],基于上述方法所得到的姿轨耦合动力学模型适应于任意轨道形式,并且其状态变量无需复杂的滤波便可很容易地测量,且具有明显的物理意义。

文献[13]中提出的非奇异终端滑模控制在克服传统线性滑模指数收敛慢缺点的同时,又解决了终端滑模存在奇异的缺点。但是,传统滑模控制在实际应用中常以边界层方法削弱抖颤,例如利用饱和函数代替符号函数等,边界层方法导致系统的滑动模态并未真正停留在滑模面上,而是在其附近的一个领域内,致使滑模控制所具有的强鲁棒性、对参数变化不敏感等优势未能真正发挥。针对滑模控制中存在的“抖颤”现象,文献[14-16]提出应用高阶滑模的控制思想,通过对控制律导数的设计,从而达到消除抖颤且兼顾滑模控制高精度、强鲁棒性等优势的目的。

基于上述研究,本文针对逼近自由翻滚目标的姿轨耦合控制问题,在考虑控制指令耦合、外干扰及参数不确定性的基础上,设计了无抖颤的二阶非奇异终端滑模(secondordernonsingularterminalslidingmode,SONTSM)控制器。首先,基于视线坐标系建立了适应于任意轨道形式的相对运动模型,结合修正罗德里格参数(modifiedRodriguesparameters,MRP)描述的相对姿态模型,建立了六自由度姿轨耦合一体化模型。在此基础上,设计了非奇异终端滑模面,通过对控制输出导数的设计并对其进行积分处理,从而消除了传统滑模的抖颤问题,实现了系统的高精度、强鲁棒性的控制目标。所设计的自适应律避免了传统终端滑模控制需要干扰界先验信息的限制。最后,设计了与经典控制方法的对比仿真实验,以验证所设计控制器的正确性及控制性能。

1　模型建立

1.1视线坐标系

考虑到目标航天器轨道参数有可能未知,以及当其存在轨道机动时,将不再运行于开普勒轨道,此外也考虑到工程实际中的敏感器测量,本文将首先基于视线坐标系推导得到相对轨道动力学方程,并进一步结合相对姿态动力学方程最终得到类拉格朗日形式的姿轨耦合动力学模型。

地心惯性坐标系与视线坐标系示意图如图1所示,OiXiYiZi为地心惯性坐标系,OlXlYlZl为视线坐标系。在视线坐标系中,将追踪航天器的质心作为其原点Ol,由追踪航天器质心指向目标航天器质心的矢量为其Xl轴,Xl轴与Yi轴确定的平面内与Xl轴垂直且指向Yi一侧的矢量为其Yl轴,Zl轴与Xl轴、Yl轴垂直,符合右手法则。qε表示视线倾角,qβ表示视线偏角。rc、rt分别为由地心指向追踪航天器质心和目标航天器质心的位置矢量。

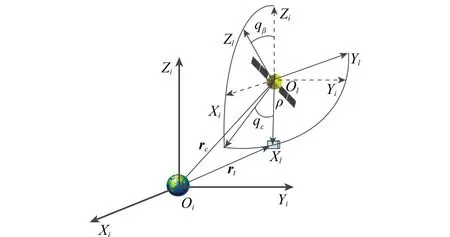
图1　地心惯性坐标系与视线坐标系Fig.1　Inertial frame and line of sight frame

1.2相对轨道动力学

视线坐标系下的相对轨道动力学方程[10]为

(1)

(2)

将用矢量形式描述的相对轨道动力学方程式写成分量形式

(3)

式中,ρ为追踪航天器与目标航天器间的相对距离；qε，qβ分别表示视线倾角和视线偏角;ax,ay,az为控制加速度在视线坐标系下的分量;fdx,fdy，fdz为外界干扰加速度在视线坐标系下的分量。为方便后续控制器设计,需将上述分量形式的相对轨道动力学方程写成类拉格朗日形式的紧凑形式

(4)

式中

1.3相对姿态动力学

本节将分别建立追踪航天器和目标航天器的姿态动力学和姿态运动学方程,进一步得到航天器相对姿态动力学模型。

由刚体动量矩定理可得追踪航天器的姿态动力学方程[4],即

(5)

式中,Jc表示追踪航天器转动惯量；ωc表示追踪航天器角速度在本体坐标系下的表示；τ为姿态控制力矩；τd为外界干扰力矩。

考虑到追踪航天器在与目标航天器进行姿态同步旋转的过程中存在大角度机动,为避免姿态控制中存在奇异,本文使用MRP参数描述航天器的姿态运动,则追踪航天器的姿态运动学方程为

(6)

式中,σc为追踪航天器姿态的MRP参数。

同理,目标航天器的姿态动力学和姿态运动学方程分别为

(7)

(8)

式中,Jt表示目标航天器转动惯量;ωt表示目标航天器角速度;σt为用以描述目标航天器姿态的MRP参数。

定义两航天器之间的姿态偏差为σe,其具体表达式为

(9)

两航天器间的误差角速度可由式(10)得到

(10)

式中,ωe为两航天器间的误差角速度;R为由目标航天器本体系到追踪航天器本体系的转换矩阵。R的具体表达式为

(11)

则两航天器间的姿态偏差动力学方程为

(12)

式中

对式(12)求导,整理可得类拉格朗日形式的姿态偏差动力学方程为

(13)

式中

1.4姿轨一体化动力学模型

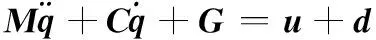
(14)

式中

假设 1假设在追踪航天器x轴正轴上安装其对接口或抓捕装置(如空间机械臂),在目标航天器x轴负轴上安装相应的对接口,故两航天器最终交会对接时满足关系σc-σt=0。

2　参考轨迹设计

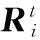
(15)

式中,ρi为惯性坐标系下的特征位置向量;xi、yi、zi为ρi在地心惯性坐标系下的分量。

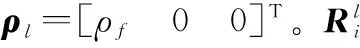
(16)

由式(15)和式(16)可以得到视线倾角和视线偏角的期望值qεd、qβd。

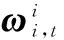
(17)

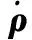
(18)

(19)

式中

(20)

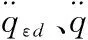
3　自适应二阶终端滑模控制器设计

基于系统式(14)所示的姿轨一体化动力学模型,考虑系统中存在参数不确定性及未建模动态,可以进一步得到姿轨一体化动力学方程,即

(21)

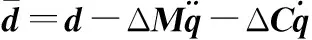
(22)

在进行控制器设计前,首先给出如下合理假设:

假设 2在对非合作目标的逼近过程中,追踪航天器与目标航天器间的相对运动和相对姿态信息可测、光滑且有界。

为了便于后文对系统稳定性进行分析,现给出一个关于非线性系统稳定性的引理。

引理 1[17]若存在一个连续函数V(t)使得如下条件成立:

(1)V(t)正定；

(2) 存在实数c>0,α∈(0,1)以及一个原点的开邻域使得

(23)

则系统在有限时间内稳定,且收敛时间满足

(24)

定义系统的状态偏差为

e=q-qd

(25)

则状态偏差的一阶导数及二阶导数分别为

(26)

(27)

(28)

定义线性滑模面为

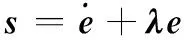
(29)

式中,λ=diag(λ1,λ2, …,λ6),λi>0,i=1,2,…,6；且定义s=[s1,s2, …,s6]T,si>0,i=1,2,…,6。为应用非奇异终端滑模控制理论进行控制律设计,需要定义非奇异终端滑模面σ。

(30)

式中,β=diag(β1,β2, …,β6),βi>0,i=1,2,…,6；p和q为正奇数,且满足1

(31)

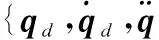
(32)

(33)

(34)

(35)

(36)

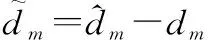
(37)

式中,γ0>0为待设计参数。对式(37)求导可得

(38)

进一步有

(39)

式中

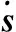
(40)

式中,σmax(0)=‖σ(0)‖∞。本文将进一步证明在终端滑模面σ=0上,滑模面s也将在有限时间ts内到达s=0平面内。定义Lyapunov函数

(41)

V2在终端滑模面σ=0上对时间求导,可得

(42)

式中,βmin为β中绝对值最小的分量；

设滑动模态s在有限时间ts内收敛至0,则由引理1可知,当t≥ts时,s(t)=0,且满足

(43)

证毕

注 2传统通过引入边界层的方法[13]抑制滑模抖颤虽能保证控制器输出连续,但却失去了不变性这个显著优点,使得控制精度变低以及系统鲁棒性变差。本文在控制器设计中借鉴了高阶滑模的设计思想,保持了传统滑模具有不变性的优点,消除了抖振,并保持了控制精度。

注 3由控制律式(34)～式(35)整理可得

(44)

注意到式(44)本质上是一个低通滤波器,该滤波器以方程右端信号为输入,以控制器u为输出,这在理论上解释了本文所设计的控制器可以消除滑模控制抖颤问题的原因。

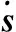
(45)

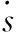
4　仿真分析

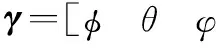
(46)

(47)

式中,R(σt)为地心惯性坐标系与目标航天器本体系之间的转换矩阵。

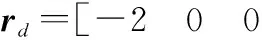
(48)

作用在追踪航天器上的干扰力矩(单位:N·m)模型取为

(49)

式中,A0=1.5×10-5N·m；ω0为轨道角速度；N(0,v)表示均值为零且方差为v的高斯白噪声。本文取vρ=10-5,vσ=10-5。

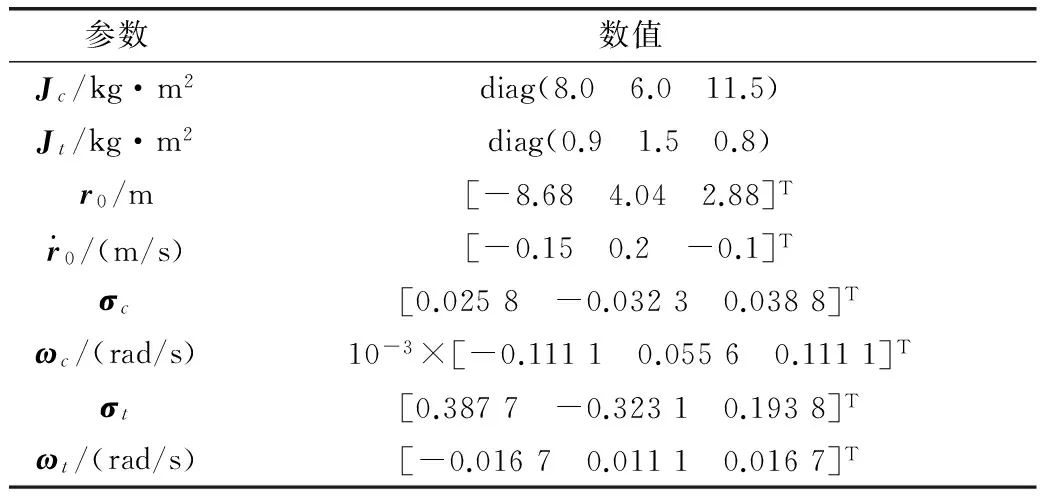
表1　仿真参数

本文所设计的SONTSM控制器参数选取为

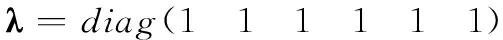
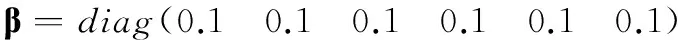
为了验证本文所提SONTSM控制器在动态特性、控制输出及鲁棒性等方面的性能,将本文提出的控制方法与文献[12]中的经典PD控制以及文献[19]中的线性滑模控制(sliding mode control, SMC)作比较,将控制输出及收敛时间调整至大致相等的范围内,得到如图2～图5所示的变化曲线。图2和图3分别为两航天器间的相对位置变化曲线和相对姿态欧拉角变化曲线。图4和图5分别给出了控制加速度和控制力矩的变化曲线。

由图2和图3可知,3种控制器均能完成预期的控制目标,但相对于PD和SMC,本文的SONTSM具有更短的收敛时间和更高的控制精度,使得追踪航天器在约30 s内到达期望位置,在10s内便完成了初始姿态最大值约76°的大角度机动,实现与目标航天器的姿态同步。需要说明的是,图3在用欧拉角描述姿态角变化时出现了奇异,而事实上，本文所使用的MRP并不存在奇异现象。图4和图5表明，在姿轨耦合控制初期需要较大的控制加速度和控制力矩,这是由于初始相对位置和相对姿态偏差较大而引起的,后期只需较小的控制加速度和控制力矩便可实现对期望相对位置和姿态的跟踪。由图4和图5可知,SMC出现了明显的抖颤现象,而本文SONTSM控制方法不仅具有较小的控制输出,更重要的是克服了传统滑模控制方法中的抖颤现象,且保持了滑模不变性,从而兼顾了系统鲁棒性和控制精度,其控制输出的连续使得该方法具有工程可实现性。

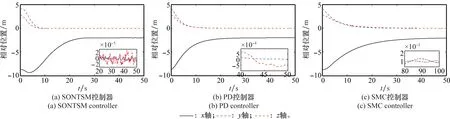
图2　目标航天器本体坐标系下的相对位置Fig.2　Relative position in the body coordinate frame of target

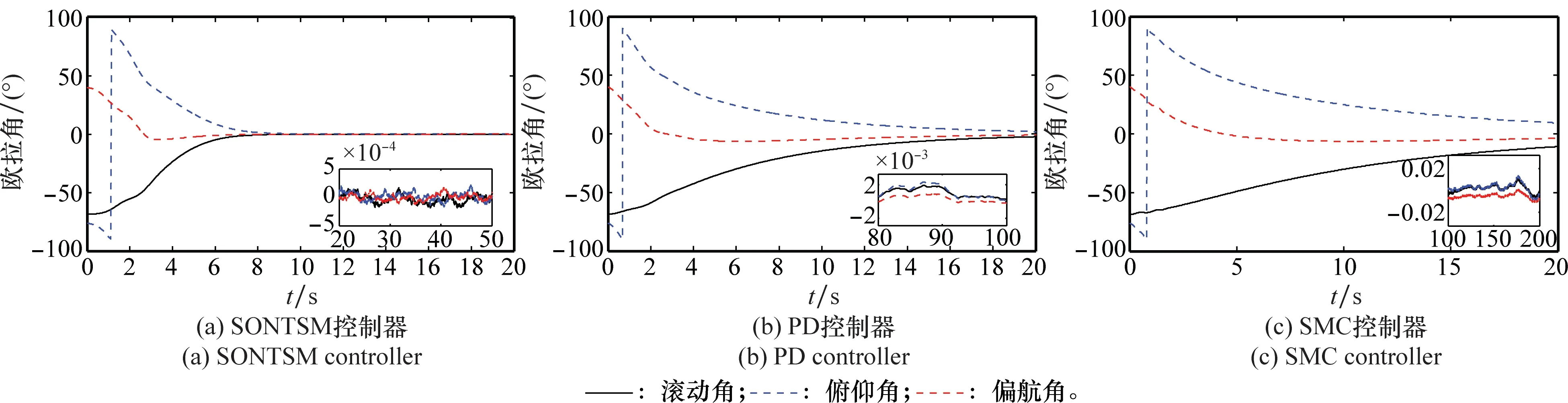
图3　相对姿态角Fig.3　Relative attitude angle

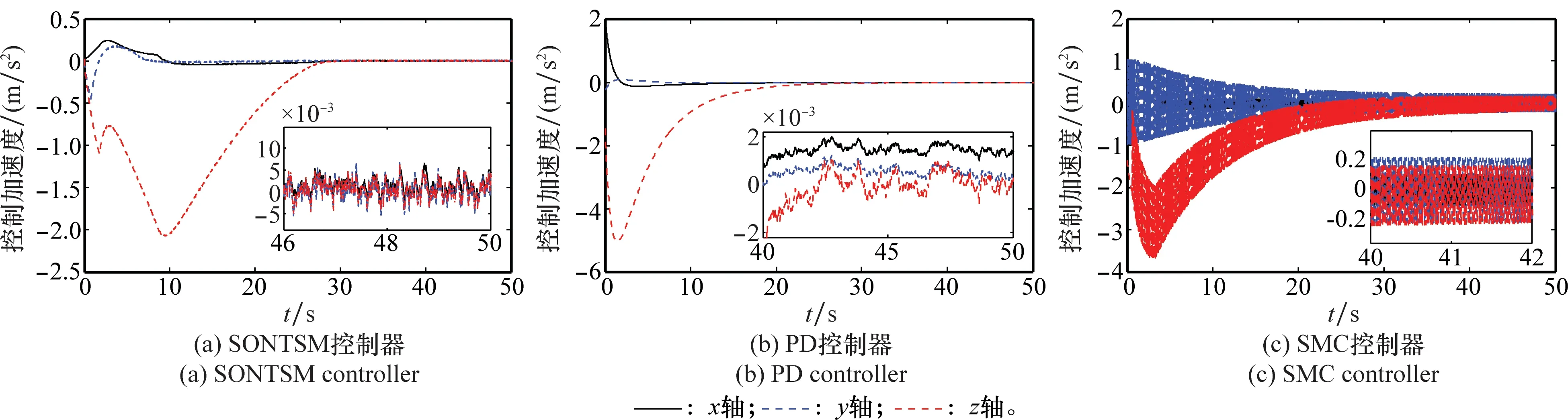
图4　控制加速度Fig.4　Control acceleration

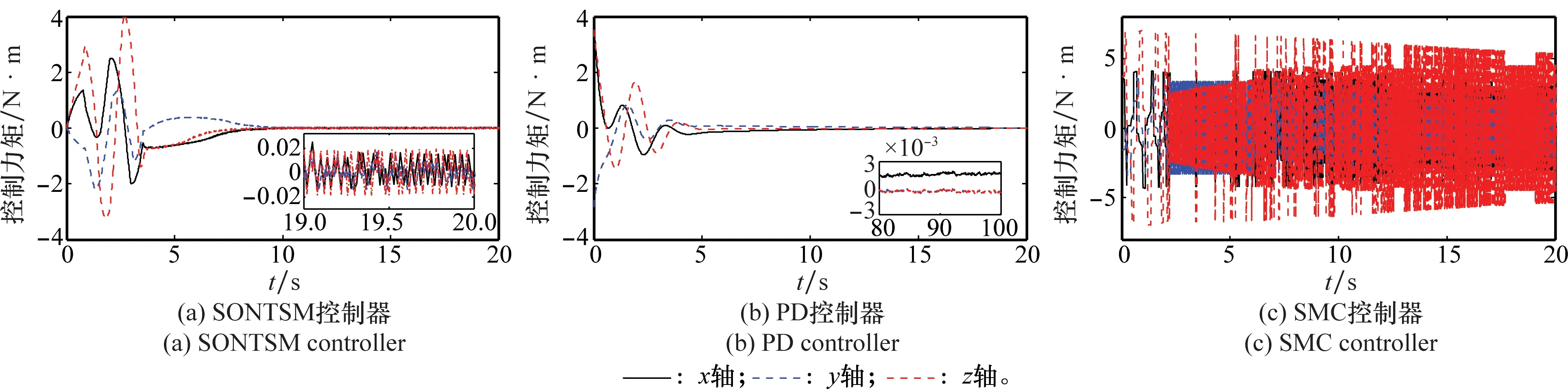
图5　控制力矩Fig.5　Control torque

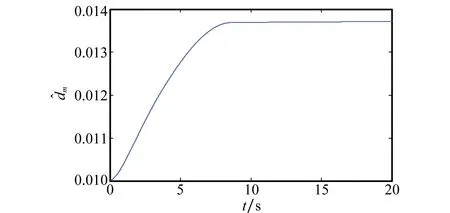
图6　复合干扰导数界的估计曲线Fig.6　Compound disturbance boundary estimation

为了在系统鲁棒性方面对3种控制方法加以比较,本文将系统干扰的数量级由10-5提高至10-1,图7和图8给出了这一强干扰下3种控制方法作用下的两航天器间地心惯性坐标系下相对位置和目标航天器本体坐标系下相对姿态的三维运动曲线。由图7可知,PD和SMC控制下的追踪航天器均已偏离期望位置,无法满足航天器逼近要求。本文SONTSM控制下的追踪器则依然能够很好地收敛于期望位置,具有很强的鲁棒性。图8则表明在这一强干扰下,PD控制下的追踪航天器姿态已无法与目标航天器实现姿态同步,而本文的SONTSM与SMC仍可完成任务。

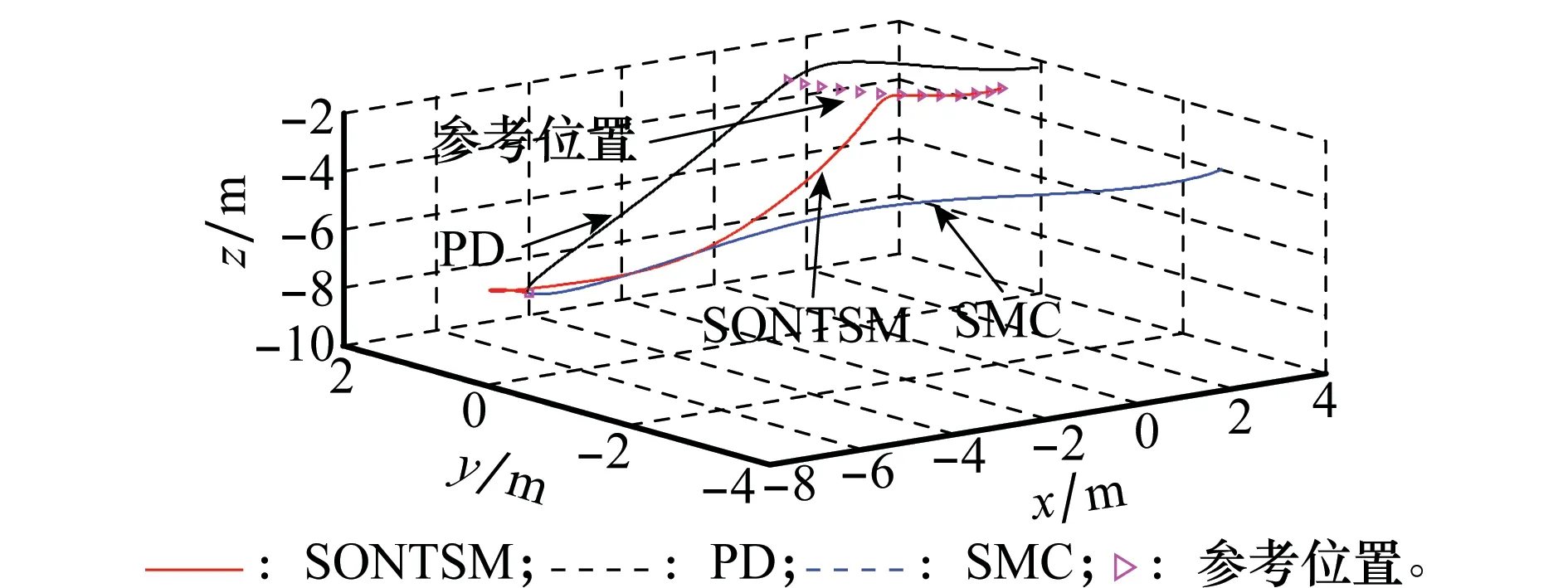
图7　强干扰下两航天器的相对位置图Fig.7　Relative position versus time with strong disturbance

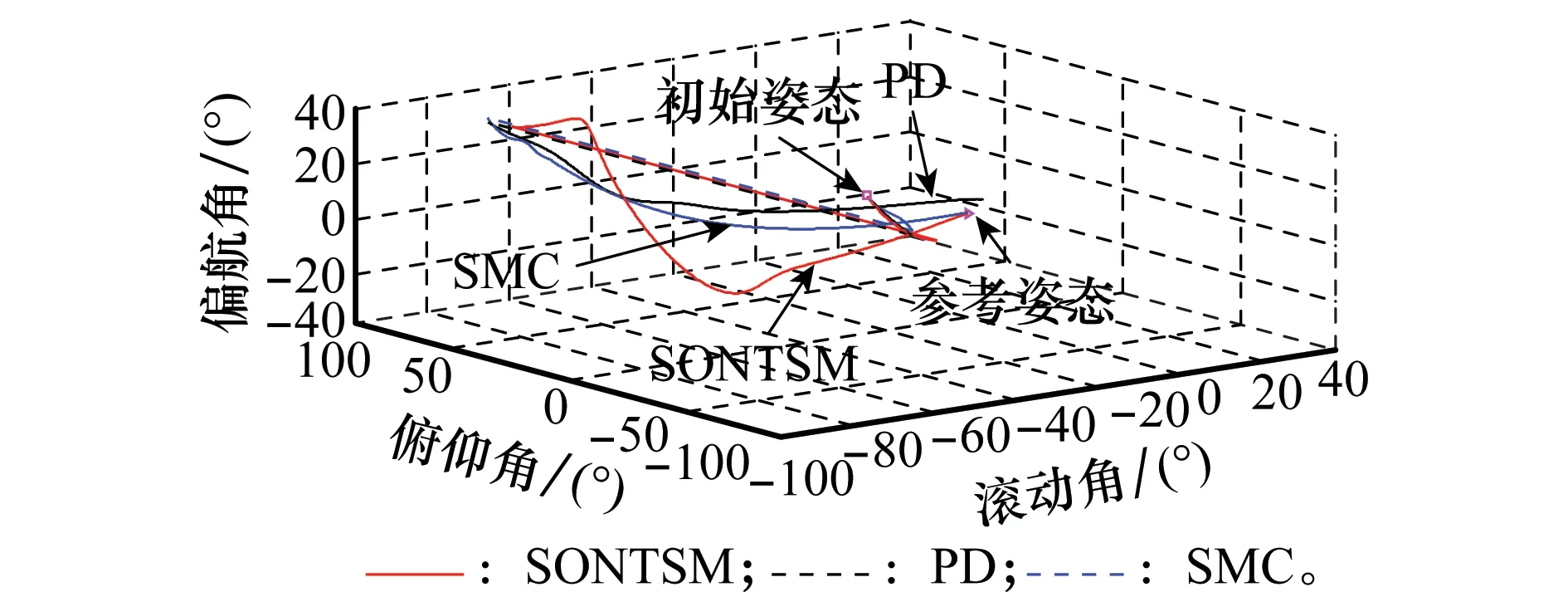
图8　强干扰下两航天器的相对姿态Fig.8　Relative attitude angle versus time with strong disturbance

为了评价和比较在对目标航天器逼近过程中的能量消耗,由最优控制导出的性能指标函数定义为

(50)

本文取T=50 s,图9给出了3种控制方法的能量消耗柱状图。由图9可知,在系统收敛至期望状态的过程中,本文提出的SONTSM方法能量消耗最小。

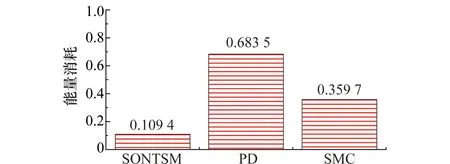
图9　不同控制方法下的能量消耗对比Fig.9　Energy consumption comparision of different controllers

将3种控制律在调节时间、稳态精度和能量消耗等方面的控制性能归纳如表2所示。由表2可知,本文的SONTSM相对于另外两种控制方法,具有收敛快、精度高且能量消耗小的优势。

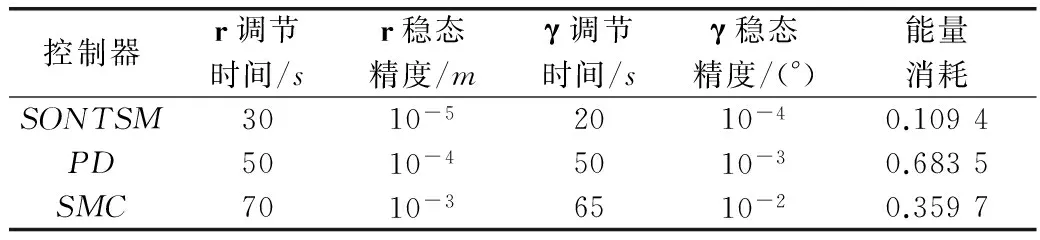
表2　3种控制控制律的控制性能对比

5　结　论

本文对逼近自由翻滚非合作目标的姿轨耦合控制问题进行了研究,首先建立了不依赖目标轨道参数的六自由度相对运动模型,同时考虑系统不确定性、外部干扰以及滑模控制中的抖颤问题,设计了无滑模抖颤的自适应SONTSM控制器并给出了稳定性证明。该控制器在继承传统非奇异终端滑模控制优点的同时,克服了抖颤现象。通过仿真验证了控制器的正确性和有效性,并与经典PD控制和传统SMC方法对比,仿真对比结果表明,本文所提出的SONTSM方法在克服抖颤现象及保持滑模不变性的同时,具有鲁棒性强、收敛快、精度高和能量消耗小的优势。

[1]HuY,XuLJ,XieYC.Controlforrendezvousanddockingwithatumblingtargetspacecraft[J].Journal of Astronautics, 2015, 36(1): 47-57.(胡勇,徐李佳,解永春.针对失控翻滚目标航天器的交会对接控制[J].宇航学报,2015,36(1):47-57.)

[2]MengZ,RenW,CaoY,etal.Leaderlessandleader-followingconsensuswithcommunicationandinputdelaysunderadirectednetworktopology[J].IEEE Trans. on Systems, Man and Cybernetics, Part B: Cybernetics, 2011, 41(1): 75-88.

[3]WeissA,BaldwinM,ErwinRS,etal.Modelpredictivecontrolforspacecraftrendezvousanddocking:strategiesforhandlingconstraintsandcasestudies[J].IEEE Trans. on Control System Technology, 2015, 23(4): 1638-1647.

[4]SunL,HuoW.Robustadaptiverelativepositiontrackingandattitudesynchronizationforspacecraftrendezvous[J].Aerospace Science and Technology, 2015(41): 28-35.

[5]ZhangQZ,JinYQ,KangZY,etal.Coupledcontrolofrelativepositionandattitudeforservicingspacecraftapproachingthetargetincloseproximity[J].Systems Engineering and Electro-nics, 2015, 37(1): 141-147.(张庆展,靳永强,康志宇,等. 服务航天器超近程逼近目标的相对姿轨耦合控制[J].系统工程与电子技术,2015,37(1):141-147.)

[6]YangJ,LiSH,SuJY,etal.Continuousnonsingularterminalslidingmodecontrolforsystemswithmismatcheddisturbances[J].Automatic, 2013, 49(7): 2287-2291.

[7]LanQX,YangJ,LiSH.Finite-timecontrolfor6DOFspacecraftformationflyingsystems[J].Journal of Aerospace Engineering, 2015, 28(5): 1-19.

[8]ChenBL,GengYH.Supertwistingcontrollerforon-orbitservicingtonon-cooperativetarget[J].Chinese Journal of Aeronautics, 2015, 28(1):285-293.

[9]JiangBY,HuQL,ShiZ.Relativepositionandattitudecoupledcontrollerdesignforapproachinganddockingwithafreelytumblingtarget[J].Journal of Astronautics, 2014, 35(1): 54-60. (姜博严,胡庆雷,石忠.与自由翻滚目标近距离段交会对接的相对姿轨耦合控制[J].宇航学报, 2014, 35(1): 54-60.)

[10]GaoDW,LuoJJ,MaWH.Nonlinearoptimalcontrolofspacecraftapproachingandtrackinganon-cooperativemaneuveringobject[J].Journal of Astronautics, 2013, 34(6): 773-781.(高登巍,罗建军,马卫华.接近和跟踪非合作机动目标的非线性最优控制[J].宇航学报,2013, 34(6): 773-781.)

[11]MingX,PanHJ.Nonlinearoptimalcontrolofspacecraftapproachingatumblingtarget[J].Aerospace Science and Technology, 2011, 15(2): 79-89.

[12]LuW,GengYH,ChenXQ,etal.Coupledcontrolofrelativepositionandattitudeforon-orbitservicingspacecraftwithrespecttotarget[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(5):857-865.(卢伟,耿云海,陈雪芹,等.在轨服务航天器对目标的相对位置和姿态耦合控制[J].航空学报,2011, 32(5): 857-865.)

[13]FengY,YuXH,HanFL.Onnonsingularterminalsliding-modecontrolofnonlinearsystems[J].Automatic,2013,49(6):1715-1722.

[14]SanjoyM,ChitralekhaM.Adaptivesecondorderterminalslidingmodecontrollerforroboticmanipulators[J].Journal of the Franklin Institute, 2014, 351(4): 2356-2377.

[15]FengY,HanFL,YuXH.Chatteringfreefull-ordersliding-modecontrol[J].Automatic, 2014, 50(4): 1310-1314.

[16]LiHR,JiangZB,KangN.Slidingmodedisturbanceobserver-basedfractionalsecond-ordernonsingularterminalslidingmodecontrolforPMSMpositionregulationsystem[J].Mathematical Problems in Engineering, 2015(2015)：1-14.

[17]MoulayE,PerruquettiW.Finitetimestabilityconditionsfornon-autonomouscontinuoussystems[J].International Journal of Control, 2008, 81(5): 797-803.

[18]LevantA.Higherorderslidingmodes,differentiationandoutput-feedbackcontrol[J].International Journal of Control, 2003, 76(9/10): 924-941.

[19]LiJR,LiHY,TangGJ.Adaptiveslidingmodecontrolforapproachtouncontrolledrotatingsatellite[J].Journal of Astronautics,2011,32(4):815-822.(李九人,李海阳,唐国金.对无控旋转目标逼近的自适应滑模控制[J].宇航学报, 2011, 32(4): 815-822.)

Adaptive second order terminal sliding mode control forapproachtonon-cooperativetarget

LIU Hai-long, SHI Xiao-ping, ZHANG Jie, BI Xian-ting

(Control and Simulation Center, Harbin Institute of Technology, Harbin 150001, China)

Theproblemofcoupledrelativeorbitandattitudeforapproachingtoanon-cooperativetargetisresearched.Withtheconsiderationofcoupledfactorsofcontrolcommand,systemuncertaintyanddisturbance,thechatteringfreeadaptivesecondordernon-singularterminalslidingmode(SONTSM)controllawisproposed.Firstly,therelativepositionandrelativeattitudemodelbasedonthelineofsightcoordinateframeandbodycoordinateframerespectivelyisestablished.Basedontheterminalslidingmodetheoryandinspiredbythehighorderslidingmodecontrol,thecontrollerovercomesthechatteringphenomenonthatappearsinthetraditionalslidingmode,whichalsohastheadvantagesofrapidconvergence,highprecision,strongrobustnessandsmallerenergyconsumption.BasedontheLyapunovtheory,thesystemstabilityisproved.Simulationresultsdemonstratethevalidityandeffectivenessoftheproposedcontrollaw.

non-cooperativetarget;relativemotion;terminalslidingmode;coupledcontrol;secondorderslidingmodecontrol

2015-12-07；

2016-04-25；网络优先出版日期：2016-06-22。

国家自然科学基金(61203191)；航空科学基金(20140177006)资助课题

V448.2

ADOI:10.3969/j.issn.1001-506X.2016.10.19

刘海龙(1987-),男,博士研究生,主要研究方向为飞行器控制、非线性控制。

E-mail:11B904016@hit.edu.cn

史小平(1965-),男,教授,博士,主要研究方向为系统仿真、飞行器控制。

E-mail:sxp@hit.edu.cn

张杰(1987-),男,博士研究生,主要研究方向为飞行器控制、图像处理。

E-mail:396200648@qq.com