基于网格PRM的无人机多约束航路规划

2016-10-18曾国奇赵民强刘方圆丁文锐

系统工程与电子技术 2016年10期

关键词：航路约束条件航迹

曾国奇, 赵民强, 刘方圆, 丁文锐

(1. 北京航空航天大学无人驾驶飞行器设计研究所, 北京 100191;2. 北京航空航天大学电子信息工程学院, 北京 100191)

基于网格PRM的无人机多约束航路规划

曾国奇1, 赵民强2, 刘方圆2, 丁文锐1

(1. 北京航空航天大学无人驾驶飞行器设计研究所, 北京 100191;2. 北京航空航天大学电子信息工程学院, 北京 100191)

目前，无人机航路规划技术存在约束条件少,不能满足实际飞行需求,规划效率低等不足,文章主要针对上述问题提出改进措施。首先,将航路约束条件进行分类,提出了基本约束、平台安全约束和链路载荷约束,并对约束条件建模,完善无人机航路约束模型。为了提高无人机航路规划效率,提出了网格概率地图法(gridprobabilisticroadmap,GPRM),利用约束模型构建代价函数,实现无人机航路的多约束快速航路规划。GPRM的实验仿真表明，GPRM规划效率相比较传统PRM有显著提升,同时规划结果更加符合实际任务需求,证明基于GPRM的无人机航路规划具有一定的工程应用价值。

无人机; 航路规划; 网格概率地图法; 多约束; 链路载荷

0　引　言

近年来,无人机技术取得了迅速发展,其指挥控制系统正在朝着自主化、智能化方向发展,无人机航路规划是实现无人机自主化的重要技术环节。无人机航路规划是指无人机在得到任务信息后根据执行任务的环境信息规划出满足一系列约束条件和性能指标的最优或较优的可行航路。高效的航路规划系统可以使无人机在恶劣环境中安全、高效地完成任务。因此,无人机航路规划技术吸引了越来越多学者的关注。

航路规划算法通常分为几何方法、数学规划方法、人工势场法[1]和智能优化方法[2]。几何方法一般指基于图论的搜索方法,如基于概略图的通视图法、Voronoi法[3]、概率地图法(probabilisticroadmapmethod,PRM)、A*算法,以及基于栅格的搜索方法。数学规划方法包括动态规划法、非线性规划法等。人工势场法在规划空间构建人工势场,通过势场力的作用来求解。智能优化方法有进化算法[4-5]、蚁群算法[6-7]等。

PRM因具有实现简单,几何计算需求小,扩展性好而被广泛应用于路径规划问题[8]。PRM的基本思想最初由文献[8-9]提出,主要用来解决机器人的运动规划问题和其他类似问题。文献[10]对PRM中的距离参数和局部规划器的选取进行了研究,提出了一般性的参数选取指导。针对不同的应用,对PRM的改进包括提高PRM在障碍聚集区的性能[11],提高PRM图的连通性[12]等。文献[13-14]将PRM应用于类车机器人的路径规划。文献[15]利用PRM解决了自主水下航行器的路径规划。文献[16]利用改进的PRM解决了无人机低空突防的航迹规划问题。

目前，PRM在解决无人机航路规划时还存在着一些不足。首先,对无人机航路规划的约束条件考虑不够完善[9-10],没有充分考虑无人机实际飞行需求,如对通讯链路的要求。其次,无人机规划空间大,PRM在学习阶段将消耗较多时间,限制了PRM在大范围无人机航路规划中的应用。

针对上述存在的问题,本文首先结合实际需求,对真实环境中无人机航迹的约束条件进行分类和建模。其次,对传统PRM进行改进,提出网格PRM的方法,在三维空间进行采样,构建了三维的规划空间,应用网格数据结构,实现了无人机多约束条件下航路的快速规划。

1　航路规划的约束条件

无人机在复杂环境中进行航路规划时必须满足以下约束条件。第一,无人机基本约束,包括地形、人工禁飞区、无人机最小直飞距离与转弯半径、无人机最大爬升角等约束;第二,无人机平台安全约束,包括雷达威胁源、高炮威胁源等约束;第三,无人机链路载荷约束,如链路与干扰等。

根据上述约束条件对航路质量评价的影响,以上约束条件的代价函数又可分为3类：第1类为刚性代价函数,包括地形、禁飞区、航迹段直飞距离、最小转弯半径和最大爬升角约束,该指标航路的评价是二值的,即可行或不可行；第2类为成本型代价函数,如雷达威胁源,函数值越小航路评价越好；第3类为效益型代价函数,如链路与干扰,函数值越大航路评价越好。

2　约束模型

根据3类约束条件对航路质量评价的影响,对不同约束条件进行建模后获得各约束条件下的代价模型与总的代价模型。

2.1基本约束数学量与符号使用规范

2.1.1地形

记航迹段E上航点距地面高度的集合为H={h(p)|p∈E},ch为航迹段E的地形威胁代价,hmin为最小安全飞行高度,则有

(1)

2.1.2禁飞区

由于航迹段E不能穿越禁飞区,因此有代价函数

(2)

式中,cr为无人机的禁飞区代价。

2.1.3直飞距离与转弯半径

为满足最小直飞距离和最小转弯半径约束,需要同时检测当前航迹段与前后相邻航迹段的关系。

假设无人机的转弯半径恒定,如图1所示,其中AB、BC、CD分别为连续航点形成的航迹在水平面的投影,rmin为最小转弯半径,EF为航迹段BC中的无人机直飞距离。α,β分别为航迹AB与BC、BC与CD的夹角。则无人机在BC航迹段的直飞距离为

(3)

式中,l为BC段的长度。设lmin为需要满足的最小直飞距离,cs为最小直飞距离与转弯半径代价,则有

(4)

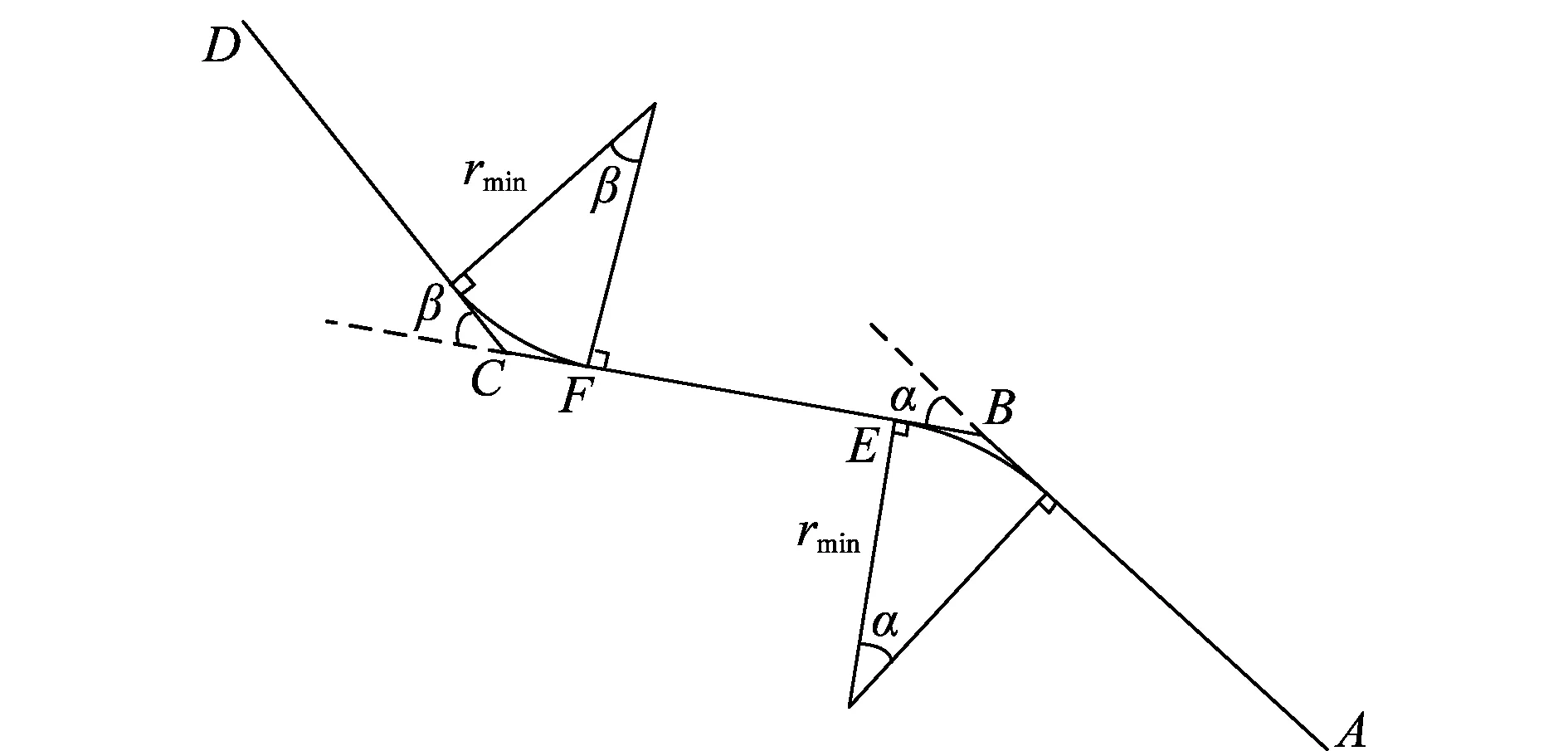
图1　转弯半径约束示意图Fig.1　Constraints of turning radius

2.1.4最大爬升角

记航迹段E的爬升角为θ,则航迹段E的爬升角代价为

(5)

式中,θmax为最大爬升角。

2.2平台安全约束

无人机平台安全约束包括雷达威胁源、高炮威胁源等,本来主要针对雷达威胁源代价进行分析,将被雷达侦测到的回波能量转化为无人机航路的代价。

由雷达特性方程可知,雷达接收到的回波功率为

(6)

式中,Pt为雷达发射功率;Gt、Gr分别为雷达发射和接收天线增益;λ为雷达波长;σ为无人机散射截面积;R为无人机与雷达距离。

记雷达的最小可检测信号功率为Simin,则由式(6)可得雷达最远作用距离

(7)

假设无人机的雷达散射截面积σ为常数时,代入式(6)有

(8)

对式(8)进行归一化,并去除极点得到距离雷达dr时的雷达威胁模型

(9)

记航迹段E上航点p距雷达距离为dr(p),则有航迹段E的雷达威胁源代价为

(10)

2.3数据链路与干扰

距链路或干扰发射天线距离为R处的信号功率密度为

(11)

记Smin为链路或干扰的最小有效功率,则可得链路或干扰的最大作用距离为

(12)

代入式(11)得

(13)

对式(13)进行归一化,并去除极点，得到距离链路或干扰d 时的模型

(14)

式中,L(d)和I(d)分别为链路和干扰模型,应用信噪比模型,记航迹段E上一航点p,有一个链路信号源,多个干扰源的情况下,点p处链路与干扰模型为

(15)

式中,LI(p)为p点的链路与干扰代价;dI_k(p)为p点距第k个干扰源的距离;dL(p)为p点距链路的距离。则航迹段E的链路与干扰的代价为

(16)

2.4航路总代价模型

由式(1)、式(2)、式(4)、式(5)、式(10)和式(16)得到无人机航路代价模型为

CT=ch+cr+cs+cp+ce+wt·ct+wl·cl=

wl·LI(d(p)))dp

(17)

式中,CT为无人机航路的总代价;ce为该航路段的欧式距离;wt为对应雷达威胁的权值系数;wl为对应链路与干扰的权值系数。

3　航路规划

3.1PRM算法分析

PRM算法是一种基于取样的规划算法,被广泛应用于地面机器人的路径规划。PRM算法分为两个阶段:第一阶段是学习阶段即地图的构造阶段；第二阶段是查询阶段[9]。

在学习阶段,PRM算法渐进增地、随机地构建出C空间中避撞点和避撞路径组成的路线图G(V,E), 其中V为图2中节点的集合,E为避撞路径(图2中的边)的集合。

在查询阶段,PRM算法采用图搜索算法在图2中搜索从起点到终点的最优路径,从而将最优路径搜索问题变成图搜索问题。查询阶段分为两步,首先将查询的起始点s和终点g分别连接到航路图中的s′和g′,然后对航路图进行搜索,找到连接s′和g′的一系列的边,这样,就是实现了从s到g的航线的搜索。图2为PRM算法在简单环境下求得的航迹。

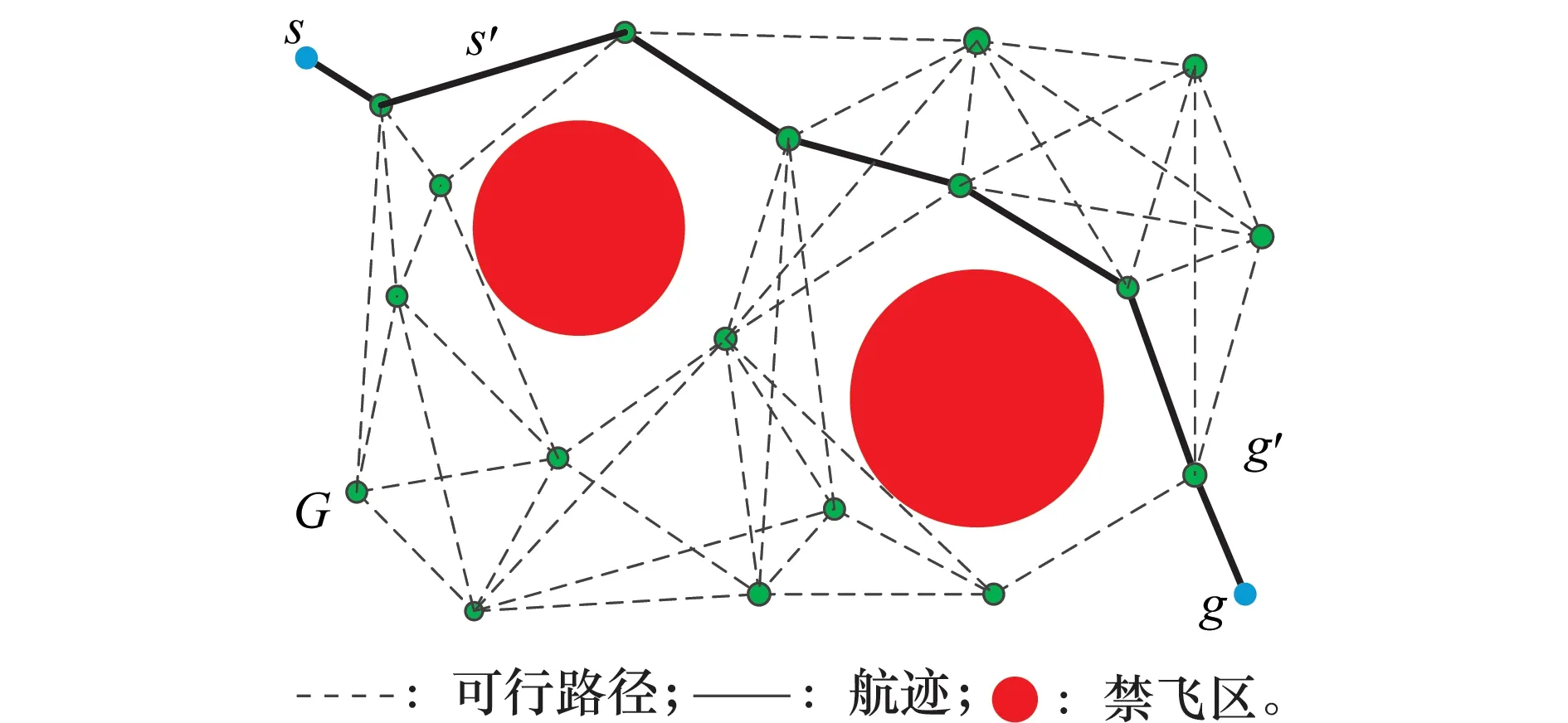
图2　PRM图和规划结果Fig.2　PRM diagram and results of plan

PRM算法在二维规划空间有着良好的性能,在地面机器人的航路规划中较多的应用,但是由于无人机的规划空间由二维拓展到三维,图2中的节点数与边数呈指数上升,该方法在无人机航路规划时存在性能较低的缺陷。为提高大范围无人机航路规划的性能,本文提出网格PRM算法。

3.2网格PRM算法学习阶段

在大范围无人机航路规划应用中,由于规划空间的高度尺度要远小于长宽尺度,采用等高度间隔采样,提出基于分层的地图构建。将规划区域以高度间隔dinterval进行分层,在每层的概率地图构造中将空间再划分为边长为Lgridsize的正方形网格,在网格种以每单位面积的密度进行随机采样。

图3为两种算法在学习阶段的流程对比图。

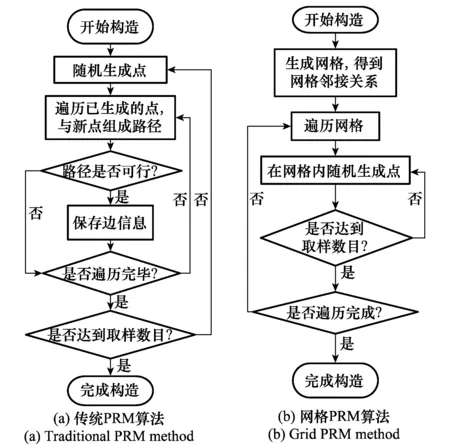
图3　两种算法在学习阶段的流程对比图Fig.3　Comparison of two methods during the learning phase

通过对比可以看出,网格PRM算法相比于传统PRM算法增加了对规划空间的网格划分,同时丢弃了对路径的地形躲避检测。在完成地图的构造之后,将地图中的边定义为当前节点与当前节点所在网格的相邻网格中的所有节点构成的边。因此,通过将空间划分为网格,使得节点的邻接关系转化为网格的邻接关系。

采用基于网格的PRM的构造方法主要有两大优势。第一,将学习阶段需要大量运算量的路径地形躲避检测推迟到查询阶段,加快学习阶段速度；同时,由于查询阶段只检测最可行的路径,大大减少了路径的地形避让检测次数,算法速度加快。第二,将采样点根据网格划分,只需要保存网格的关系,将点的关系由网格关系导出,大大减小存储空间；同时,在查询阶段可以根据网格关系,结合无人机飞行约束条件丢弃无用网格中点的扩展,进一步加快查询速度。

3.3网格PRM算法查询阶段

为了加快PRM算法查询阶段的速度,在查询阶段应用A*算法进行搜索。

3.3.1A*搜索算法分析

A*算法在搜索过程中保留两个节点表：一是open表,表中存放在节点扩展过程中已经出现但还没有检查过的节点;二是close表,表中存放在节点搜索过程中已经检查过的节点。为了提高节点搜索效率,对open表中存放的节点以一定的权值进行排列,使open表中最有希望的节点总是最先取出的。

在传统PRM图上应用A*算法在节点扩展时需要计算节点的每个相邻节点。考虑到无人机的飞行动力约束,节点的有效扩展区域如图4所示。

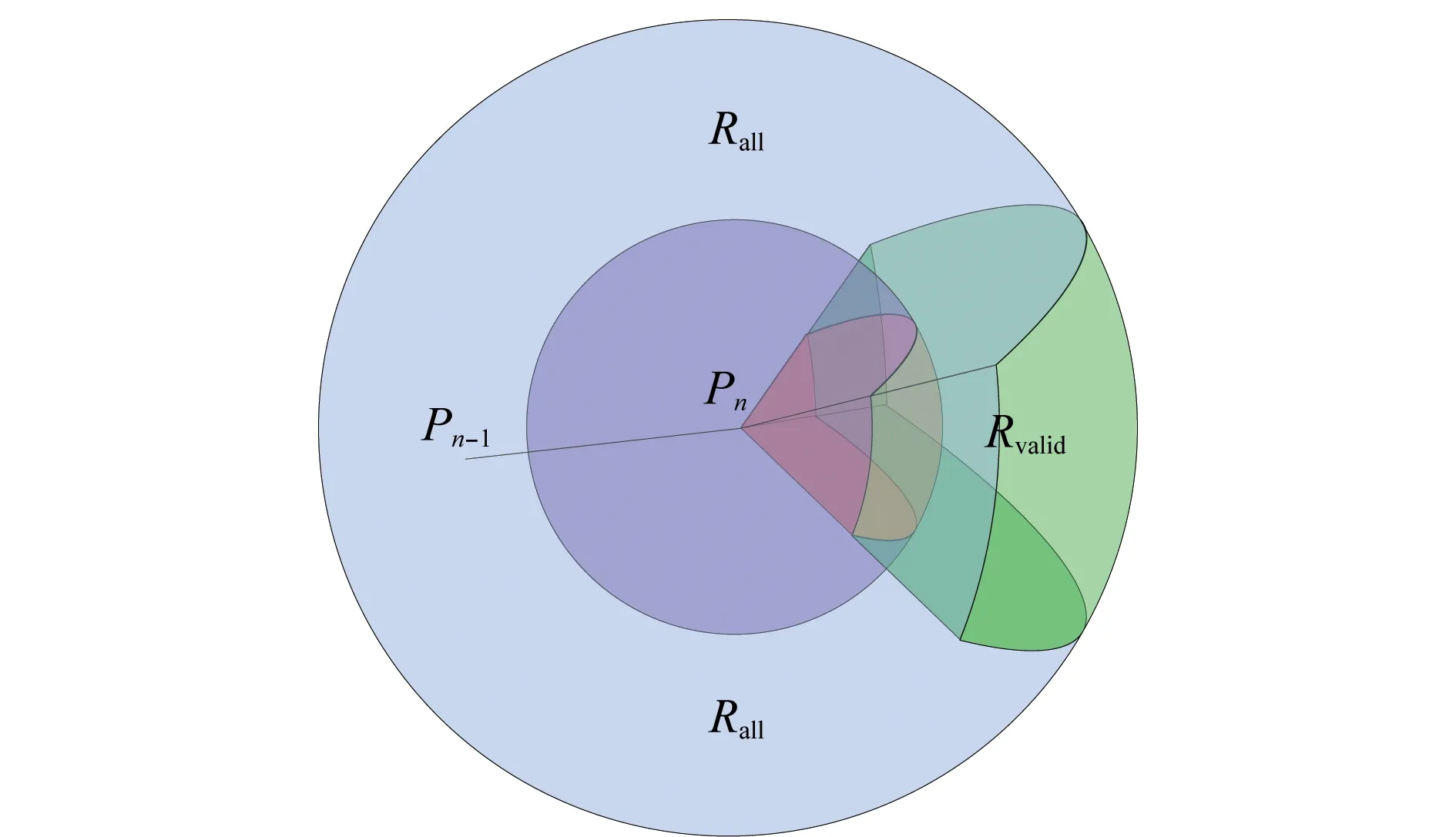
图4　节点有效扩展区域Fig.4　Node effective extension area

图4中球心Pn点为当前的节点,Pn-1点为Pn的上一节点,则图中红色球面与蓝色球面形成的球壳Rall是传统PRM算法中节点Pn的节点扩展区域,以球心为顶点的四棱锥与球壳的相交区域Rvalid是考虑无人机飞行性能后的节点有效扩展区域。

A*算法在节点扩展阶段计算每一相邻节点的航路代价并将其放入open表中,由于传统PRM中的只包含节点是否相邻的信息,因此不能利用无人机飞行约束对节点扩展进行有效缩减。网格PRM将节点分层并分块存储,可以通过快速剔除无效扩展块来加速A*算法的扩展速度。

3.3.2基于网格的A*算法节点扩展

利用网格PRM图的节点结构,得到节点的扩展流程如下。

(1) 计算当前节点所在网格的位置(x,y)和节点所在层z,根据无人机的飞行性能约束,快速计算当前节点的有效扩展块。根据当前节点是否为起始起点,可将扩展过程分为两类情况。

① 如果当前节点为起始节点P0,则当前节点的下一节点为层z、z+1、z-1中的网格位置为(x-1,y-1)、(x,y-1)、(x+1,y-1)、(x-1,y)、(x+1,y)、(x-1,y+1)、(x,y+1)、(x+1,y+1)中的节点,如图5所示。

图5　起始节点的块扩展Fig.5　Starting nodes grid extension area

② 如果当前节点Pn不是起始节点,则计算当前节点的上一节点Pn-1所在的网格位置(x,y)和节点所在的层z,根据上一节点所在网格的位置和层可以出现图6所示情况。

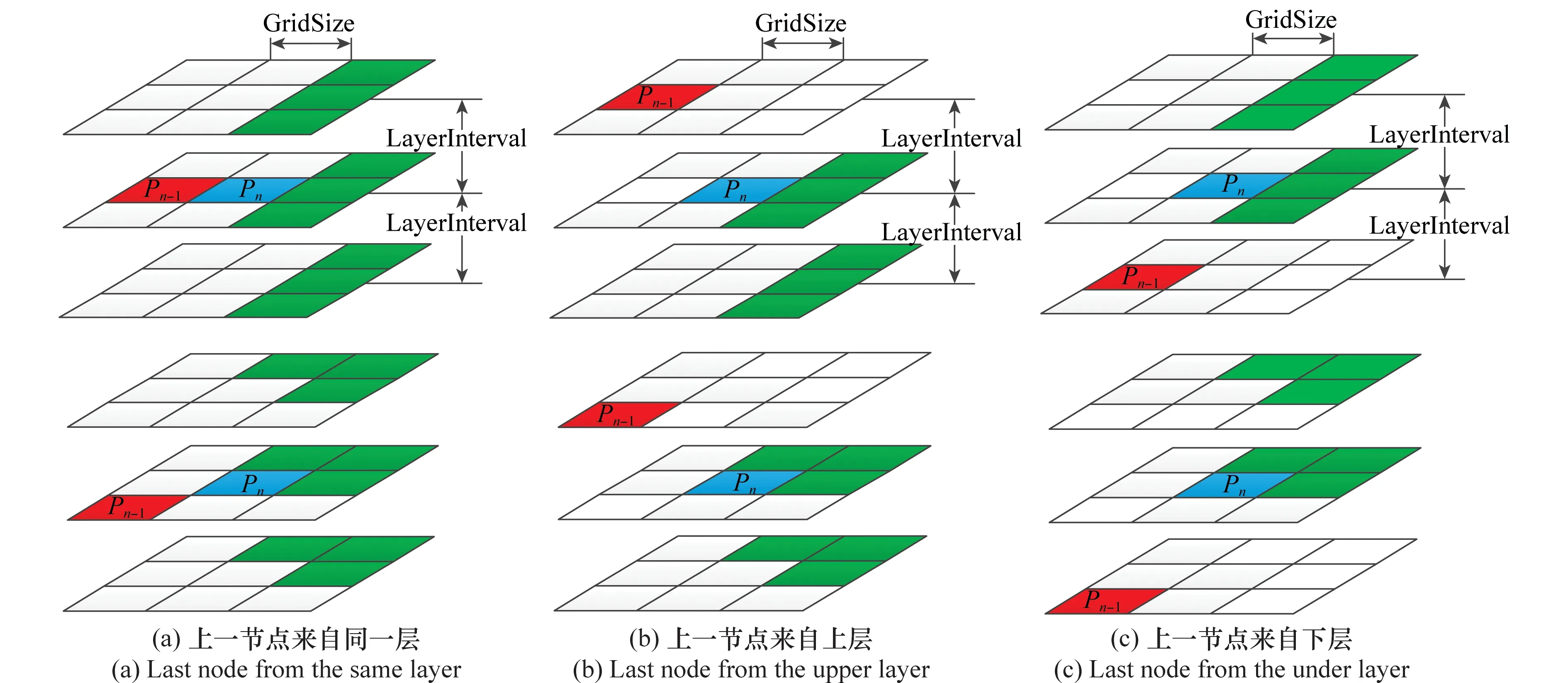
图6　普通节点的块扩展Fig.6　Ordinary nodes grid extension area

图5、图6中,蓝色网格为当前节点所在网格,红色网格为当前节点的上一节点所在网格,绿色网格为当前节点的扩展节点所在的网格。

(2) 在得到节点的扩展网格后,将扩展网格中的所有节点作为当前节点的下一节点作为A*搜索时的扩展节点。

采用新的基于网格的节点扩展方法的优势有:一是,可以有效减少由于不符合最小航迹段长度要求和较长航迹段的节点的无效扩展；二是,可以减少由于不符合无人机最小转弯半径的节点的无效扩展；三是,可以减少不符合无人机最大爬升角的航点的无效扩展。

3.3.3A*算法的函数选取

在得到当前节点的扩展节点后对所有的扩展节点进行评价。选取式(17)作为代价函数,保证了规划航迹的准确性和有效性。选取较大的启发函数可以加速算法的收敛,但过大的启发函数将使规划失去最优解,为了保证航路的确定性,将欧氏距离作为启发函数。由式(17)可知,即使在不同的权重因子的情况下,可以保证启发函数将严格小于代价函数,保证了航路规划的确定性。假设当前节点为Pcur,上一节点为Ppre,终点为Pg,则Pcur的代价为

(18)

Pcur的优先级为

Pcur·priority=Pcur·cost+ce(Pcur,Pg)

(19)

3.4算法复杂度分析

现对网格PRM和传统PRM法算法复杂度进行分析。设规划区域采样点数为N,传统PRM法在学习阶段每一节点可平均形成M条可行路径,同时网格PRM法在采样区域采样个数为m,设最终规划结果节点数为n。

3.4.1学习阶段

传统PRM:由于传统PRM在学习阶段每次采样都进行路经检测,因此时间复杂度为O(N2)。

网格PRM:网格PRM法在学习阶段不进行路经检测,时间复杂度为O(N)。

3.4.2查询阶段

传统PRM:由于传统PRM在查询阶段不能对搜索进行剪枝,因此时间复杂度为O(Mn)。

网格PRM:网格PRM法在查询阶段平均每次仅扩展6～9个网格分节点,假设平均为8个网格,则时间复杂度为O((8m)n)。通过对高度间隔dinterval及网格边长为Lgridsize的值进行选取应有关系:

M≈26m

(19)

式(19)表示网格PRM法中的网格中节点的可行路径与传统PRM法中节点的可行路径数量想当。则网格PRM法时间复杂度约为O((M/3)n)。

通过比较可知网格PRM法较传统PRM法在学习阶段和查询阶段时间复杂度有巨大优势。

4　实验验证

选取100km×100km的地形,使用Matlab绘制地形高度图,如图7所示,在地图的右下方存在高度3 000m的山脉。

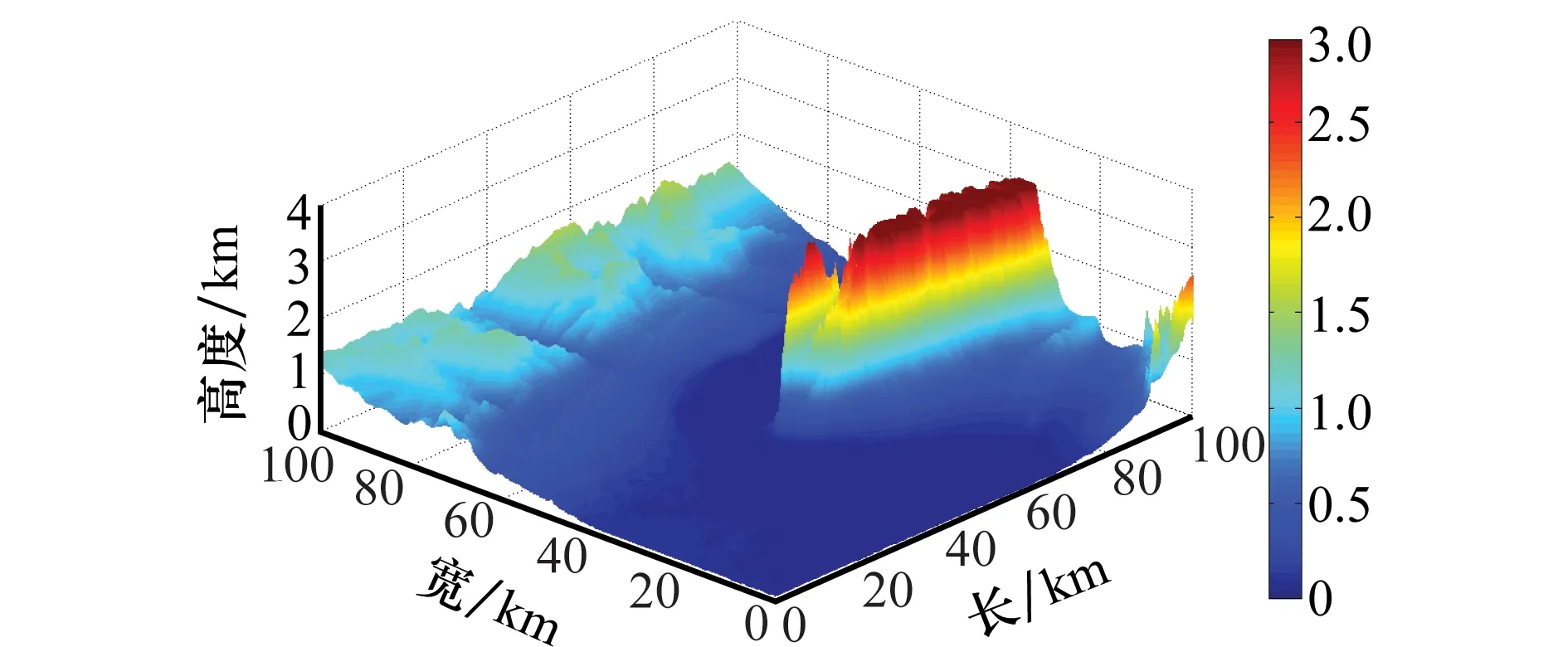
图7　高度地形图Fig.7　Topographic map

设置采样高度间隔dinterval=250m,网格边长Lgridsize=5km,每平方公里采样密度为5个。无人机最小直飞航迹段为ls=5km,最小转弯半径为rmin=1km。起始点坐标为(1km,1km,0.28km),终点坐标为(99km,99km,1.32km)。在没有禁飞区、雷达威胁源,且不考虑数据链路的情况下,得到规划航迹如图8所示。

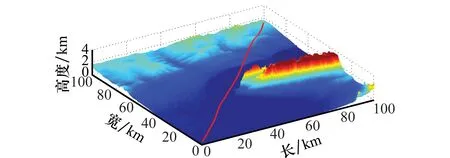
图8　场景1规划结果Fig.8　Planning results of scene 1

从图8可看出，当环境简单时,规划的航路为避开地形的从起始点到终点的近似直线。

分别在(86km,78km)和(12km,20km)处设置半径为12km的禁飞区,得到航迹如图9所示。

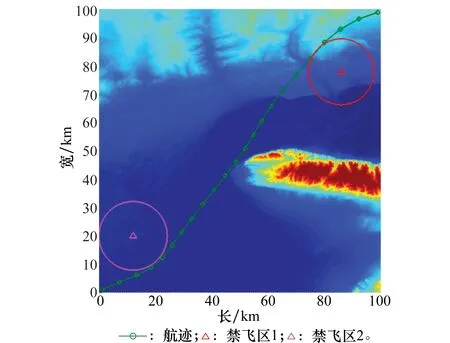
图9　场景2规划结果Fig.9　Planning results of scene 2

从图9可以看出，规划出的无人机航路成功避开了人工禁飞区,但无人机航路较图8更长。

在以上基础上增加雷达威胁源,对于小型无人机,雷达对其可侦察最大半径较常规目标缩小,因此在(35km,68km,0.482km)处设置半径为36km的雷达威胁,分别在不同的雷达威胁权重时得到如图10所示航迹。航迹1和航迹2分别为权重因子取值为5.0和1.0时的规划航迹。

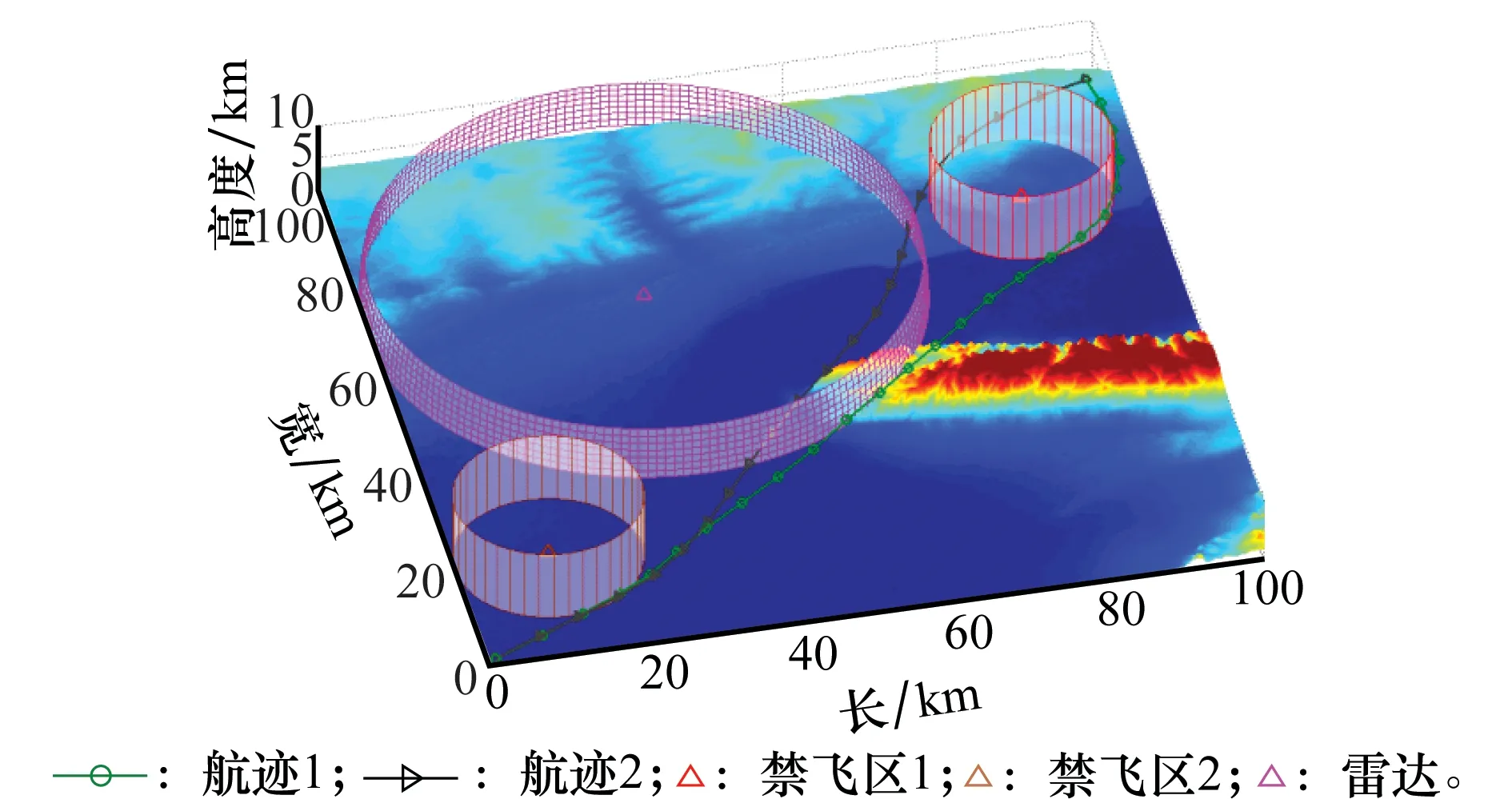
图10　场景3和场景4规划结果Fig.10　Planning results of scene 3 and scene 4

由图10可以看出,当航路的雷达威胁权重因子为1.0时航路掠过雷达威胁源,当雷达威胁权重因子为5.0时航路完全避开了威胁源,但较前者航路长度增加。因此,设置不同的雷达威胁权重因子可在航路的安全性和其他因素之间进行权衡。

当考虑无人机链路安全的因素,在(17km,92km,1.1km)处设置半径为109km的链路,在(64km,36km,0.738km)处设置半径为41km的干扰源,得到如图11所示航迹。

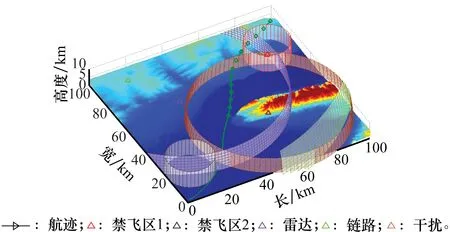
图11　场景5规划结果Fig.11　Planning results of scene 5

本文测试计算机配置如下:

CPU:Intel(R)Core(TM)i3M330 @ 2.13GHz

RAM: 4.0GB

传统PRM法和网格PRM法的航路规划耗时如表1所示。

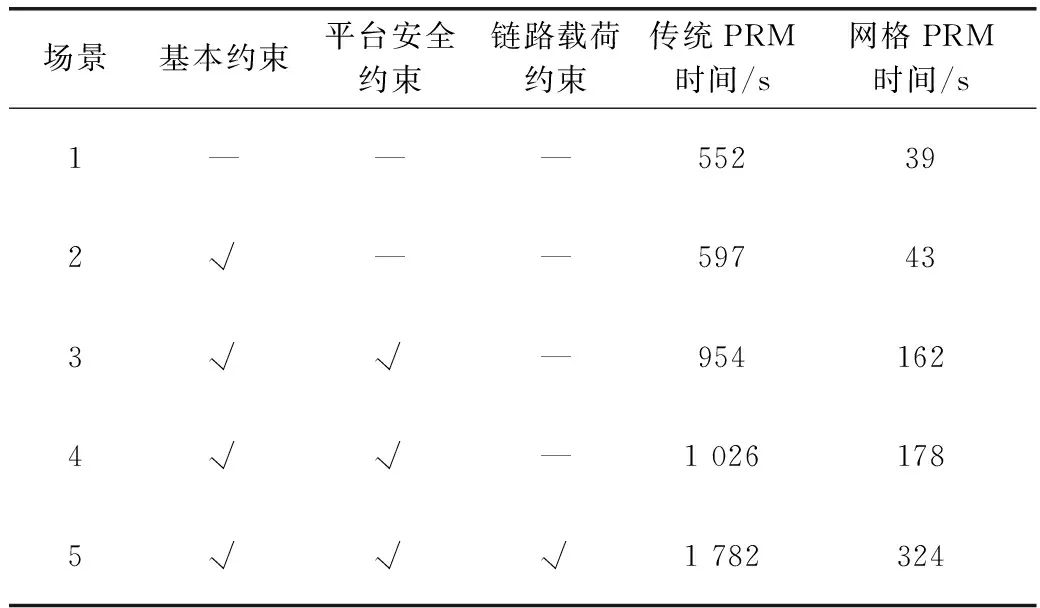
表1　航迹规划时间

由表1可知,在相同场景下网格PRM比传统PRM规划速度快5～10倍不等。同时,传统PRM法在航路规划时需要内存为1 200 MB左右,网格PRM法所需内存仅为90 MB左右,所需运行时空间显著降低。由于选取的启发函数为欧式距离函数,故两种算法都为确定性算法,因此规划结果相似。由表1可知,网格PRM法在不同的场景下,规划耗时较短,规划航路满足无人机实际飞行要求,规划速度满足离线规划要求。

5　结　论

本文针对PRM算法应用于三维航迹规划时效率低的问题,结合无人机航路规划时的约束条件,对无人机航路规划进行研究,得到了如下成果:

(1) 对无人机真实飞行时的约束条件进行分类,对不同的约束条件分别建立了模型,同时得到了约束条件的总代价模型;

(2) 提出了网格PRM算法,实现了三维空间大范围环境下的航路的快速规划；

(3) 针对典型情景进行仿真,快速规划出了满足安全性要求的无人机航路,证明了本方法的有效性和高效性。

然而，本文中的方法对于动态的环境信息不具备处理能力,今后将继续改进算法以实现无人机局部实时的航路重规划。同时,本文实现了起飞点到任务地点的航路规划,在此基础上将对无人机的载荷规划进行研究。

[1] Bellini A C, Lu W, Naldi R, et al. Information driven path planning and control for collaborative aerial robotic sensors using artificial potential functions[C]∥Proc.oftheAmericanControlConference, 2014: 590-597.

[2] Mao H B, Tian S, Chao A N, et al.UAVmissionplanning[M]. Beijing: National Defense Industry Press, 2015:82-83.(毛红保,田松,晁爱农,等.无人机任务规划[M].北京:国防工业出版社,2015:82-83.)

[3] Zhang T S, Lu Y, Zhang L, et al. UAV path planning based on improved Voronoi diagram and dynamic weights A*algorithm[J].FireControl&CommandControl,2015(2):156-160.(张淘沙,鲁艺,张亮,等.改进Voronoi图和动态权值A*算法的无人机航迹规划[J]. 火力与指挥控制, 2015(2):156-160.)

[4] Yan J L. Evolutionary algorithm based route planer for unmanned air vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.(严建林. 基于进化算法无人机航路规划技术研究[D]. 南京:南京航空航天大学, 2008.)

[5] Ozalp N, Sahingoz O K. Optimal UAV path planning in a 3D threat environment by using parallel evolutionary algorithms[C]∥Proc.oftheIEEEInternationalConferenceonUnmannedAircraftSystems, 2013: 308-317.

[6] Li D, Cao Y H, Su Y, et al. Trajectory planning for low attitude penetration based on improved ant colony algorithm[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2006, 32(3):258-262.(李栋, 曹义华, 苏媛, 等. 基于改进蚁群算法的低空突防航迹规划[J]. 北京航空航天大学学报, 2006, 32(3):258-262.)

[7] Ma G J, Duan H B, Liu S Q. Improved ant colony algorithm for global optimal trajectory planning of UAV under complex environment[J].InternationalJournalofComputerScienceandApplications, 2007，4(3):57-68.

[8] Overmars M H, Mark H. A random approach to motion planning[R].Netherlamd: Utrecht University Repository, 1992.

[9] Kavraki L E, Svestka P, Latombe J C, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J].IEEETrans.onRoboticsandAutomation,1996,12(4):566-580.

[10] Amato N M, Bayazit O B, Dale L K, et al. Choosing good distance metrics and local planners for probabilistic roadmap methods[C]∥Proc.oftheIEEEInternationalConferenceonRoboticsandAutomation, 1998: 630-637.

[11] Amato N M, Wu Y. A randomized roadmap method for path and manipulation planning[C]∥Proc.oftheIEEEInternationalConferenceonRoboticsandAutomation, 1996: 113-120.

[12] Morales M, Rodriguez S, Amato N M. Improving the connectivity of PRM roadmaps[C]∥Proc.oftheIEEEInternationalConferenceonRoboticsandAutomation, 2003: 4427-4432.

[13] Song G, Amato N M. Randomized motion planning for car-like robots with C-PRM[C]∥Proc.oftheIEEEInternationalConferenceonIntelligentRobotsandSystems, 2001:37-42.

[14] Balakirsky S, Dimitrov D. Single-query, Bi-directional, Lazy roadmap planner applied to car-like robots[C]∥Proc.oftheIEEEInternationalConferenceonRoboticsandAutomation, 2010:5015-5020.

[15] Poppinga J, Birk A, Pathak K, et al. Fast 6-DOF path planning for autonomous underwater vehicles(AUV) based on 3D plane mapping[C]∥Proc.oftheIEEEInternationalSymposiumonSafety,Security,andRescueRobotics, 2011: 345-350.

[15] Li Q R, Wei C, Wu J, et al. Improved PRM method of low altitude penetration trajectory planning for UAVs[C]∥Proc.oftheIEEEChineseGuidance,NavigationandControlConference, 2014: 2651-2654.

Multi-constraints UAV path planning based on grid PRM

ZENG Guo-qi1, ZHAO Min-qiang2, LIU Fang-yuan2, DING Wen-rui1

(1. UAV Research Academy, Beihang University, Beijing 100191, China;2. School of Electronic Information Engineering, Beihang University, Beijing 100191, China)

Nowadaystheunmannedarielvehicle(UAV)’spathplanningtechnologyhasseveraldefects,suchasfewconstraintswhichleadtodissatisfactoryofrealisticflyingdemands,lowefficiencyinpathplanning,thispapermainlydealswiththeseproblems.First,classifytheconstraintsintothreetypes,basicconstraints,platformsafetyconstraintsandlinkloadconstraints.ThenmodeltheconstraintstorefineUAVpathconstrainmodel.Next,toimprovetheplanningefficiencythegridprobabilisticroadmap(GPRM)methodisproposed.Finally,bydevisingacostfunctionusingconstraintmodels,thehighefficiencymulti-constraintspathplanningforUAVisobtained.SimulationsshowthatpathplanningusingGPRMisfasterthanthatusingtraditionalPRM,andalsonoticethatthepathobtainedbyGPRMismorerealisticfortheactualflight,thustheengineerapplicationvalueofthismethodisproved.

unmannedarielvehicle(UAV);pathplanning;gridprobabilisticroadmap(GPRM)method;multi-constraints;linkload

2015-09-20；

2016-05-31；网络优先出版日期：2016-06-22。

国家高技术研究发展计划(863计划)(2013AA122103)；中央高校基本科研业务费专项资金(YWF-14-WRJS-005,YWF-15-WRJS-001,YWF-15-GJSYS-061)资助课题

V279;TP301.6

ADOI:10.3969/j.issn.1001-506X.2016.10.13

曾国奇(1978-),男,高级实验师,博士,主要研究方向为无人机测控、电磁兼容、共形相控阵天线。

E-mail:zengguoqi@buaa.edu.cn

赵民强(1989-),男,硕士,主要研究方向为无人机任务规划。

E-mail:beyond21299@163.com

刘方圆(1989-),男,硕士,主要研究方向为无人机航路规划。

E-mail:1019365767@qq.com