检测低信噪比运动目标的改进DP算法
2016-10-18张奕群
王 硕, 张奕群
(北京电子工程总体研究所, 北京 100854)
检测低信噪比运动目标的改进DP算法
王硕, 张奕群
(北京电子工程总体研究所, 北京 100854)
研究了用于检测低信噪比目标的动态规划(dynamic programming, DP)算法。鉴于传统各DP算法对低信噪比运动目标的检测能力较弱的问题,提出了一种改进算法。该算法利用二阶Markov模型描述目标的状态转移过程,并在此基础上将DP的目标寻优过程改进为一系列二维寻优的嵌套。这样,在充分考虑目标的各种运动可能性的前提下,改进算法仍能具有较小的目标搜索范围,从而改善了DP对低信噪比运动目标的检测性能。
动态规划; 二阶Markov模型; 低信噪比; 运动点目标; 检测
0 引 言
目标检测的一般做法是先通过检测门限对原始数据进行分割,再从分割出的观测点中甄别目标。分割门限的选择要遵循两点要求:既要保证目标存在于分割后的图像中,又要保证分割后的图像是相对“干净”的,即噪声引起的虚警点较少。在对低信噪比(signal-to-noise ratio,SNR)目标检测时,上述两点要求通常难以同时得到保证,检测门限很难选择。而在实际应用中,我们总希望检测算法可以在目标距离传感器更远、目标的SNR更低时完成检测任务,因此,研究低SNR目标的检测问题很有必要。在研究过程中,人们提出了一类无需门限分割,而对原始数据中所有潜在目标进行跟踪,逐渐确定目标的实际位置并得到目标轨迹的“先跟踪后检测”(track before detect, TBD)方法。
动态规划(dynamic programming, DP)算法是一种最常见的TBD方法。为解决最优决策问题,TBD方法最初由文献[1]提出,随后文献[2-3]将之应用到信号与图像处理领域。文献[4]首先将DP算法用于低SNR目标的检测,给出了一套完整的低SNR目标检测算法[4]。在此基础上文献[5]改进评价函数,提高了算法在混合高斯噪声下的检测性能[5]。但是,这两种DP算法均需要假定目标速度来确定搜索范围——假定速度越大,搜索范围也就越大。文献[6]指出,DP算法的检测性能随搜索范围增大而下降[6],故上述两算法检测运动目标的性能较弱。为此,文献[6-10]先后提出了改进方法,其共同点是引入“目标速度”,减小了搜索范围,提高了DP算法对运动目标的检测性能。然而,该“目标速度”一般是由目标历史轨迹外推得到的。在相同时间内,SNR越低,外推的目标轨迹越容易受噪声干扰,使得对速度的估计出错,进而影响检测性能。因此,上述改进方法对SNR很低的目标的检测能力较弱。文献[11]指出,利用二阶Markov模型来描述目标的运动状态可提高目标检测性能,并给出了一种改进算法。然而,该算法的推导过程存在错误,导致算法在寻优中并没有利用二阶模型,其寻优过程仍然是一维的,事实上与Pulford方法类似。
本文深入研究了如何利用DP算法检测低SNR(特别是SNR低于2)的运动目标的问题,在Tonissen、Pulford等人的DP算法基础上,提出了一种新的基于二阶Markov模型的DP算法改进算法,改进了DP算法对低SNR运动目标的检测能力。此外,本文还给出了计算改进算法的评价函数的分布的方法,并在此基础上分析了算法的检测性能。
1 传统DP方法
1.1目标检测问题的描述
设传感器的分辨率为M×M,各像元尺寸均为Δx×Δy(Δx=Δy=Δ),且目标的成像面积远小于单个像元尺寸,可视为点目标。将各时刻k的M×M维测量矩阵表示为
(1)
式中,1≤i,j≤M;zij(k)为像元(i,j)处的测量值,且
(2)
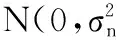

记真实的目标轨迹为
(3)
式中,上标“0”表示目标,下同。用评价函数s(θ(n),θ(n-1),…,θ(1))来衡量下述目标状态序列(θ(n),θ(n-1),…,θ(1))为目标轨迹的可能性,并将目标轨迹估计为评价函数值最大的状态序列(θ(n),θ(n-1),…,θ(1))。这样,对Θ0(n)的估计就转化为一个n维寻优问题:
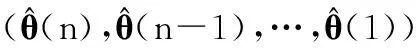


(4)
1.2Arnold的DP算法
以Arnold采用的评价函数[5]为例
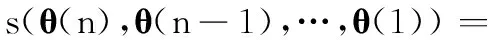
(5)
式中,Z(n)={z(n),z(n-1),…,z(1)}为连续n个时刻的测量矩阵的集合;(θ(n),θ(n-1),…,θ(1))指各时刻k(1≤k≤n)目标在θ(k)处存在的假设,与之相反,H0是在各θ(k)处无目标的假设。
由于式(4)的计算量很大,n维寻优难以在工程中应用。故为简化寻优过程,将式(5)整理为递归形式

(6)
并假设目标状态转移满足一阶Markov模型,即
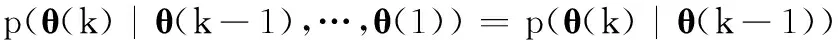
(7)
这样,将式(6)、式(7)代入式(4),n维寻优过程就可以拆分为
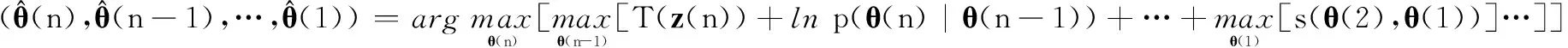
(8)
其中
(9)
在上述算法中,式(7)是关键,其假设确保了式(8)成立,使得式(4)这一n维寻优问题简化成一系列的一维寻优问题的嵌套,将算法的计算量从M2n减小为M4n。
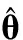
图1 DP算法的目标搜索区域RBFig.1 Search region RB of DP algorithm
然而,上述算法仅在检测运动速度不大的目标时,能够提供比较高的检测概率。这是因为,若目标运动得慢,RB可选得较小,这样寻优过程中受噪声干扰小。但若目标速度大,RB就需选得大一些,则寻优过程中受噪声干扰的机会变大,使得算法的性能下降。
为此,文献[6-10]利用“目标速度”改进并减小了DP算法对运动目标的搜索区域,提高了算法对运动目标的检测性能。以Pulford的方法为例[7],其做法是:先利用Kalman滤波由状态θ(k-1)及之前各时刻的状态来估计目标速度并外推在k时刻目标出现的范围Rθ(k-1),如图2所示。若θ(k)落在Rθ(k-1)当中,则θ(k)在往回寻优时考虑该θ(k-1),而若θ(k)落在Rθ(k-1)之外,则在寻优中该θ(k-1)不再予以考虑。这样,对DP算法来说,每一步寻优相当于只考虑RB中那一部分与目标速度一致的状态,也就减小了搜索范围。如果目标信噪比比较高、对目标速度估计得准确,上述做法的确有效缩小了目标的搜索范围,提高了检测性能。然而,若目标的信噪比很低,对目标速度的估计就可能受噪声干扰,使θ(k)被排除在Rθ(k-1)之外,导致评价函数无法沿目标轨迹有效“累积”,从而使得目标检测能力下降。
而对Barniv、Arnold的DP算法来说,由于算法考虑搜索区域内的所有状态(包括被Pulford方法排除的状态),假如目标运动得慢、搜索范围选得很小,当目标的SNR很低时评价函数反而更有机会沿目标轨迹“累积”,成功检测到目标。例如,后文的仿真结果表明,当目标的SNR很低时,Pulford方法对目标的检测能力比传统的DPA更弱。

图2 Pulford方法的搜索范围确定过程Fig.2 Search region of Pulford’s algorithm
所以,Barniv、Arnold这一类传统算法解决了对SNR很低且运动较慢的目标的检测,Tonissen、Pulford等人的改进算法解决了对SNR稍高且运动较快的目标的检测,但它们都没有很好解决对SNR很低、运动又很快的目标的检测问题。


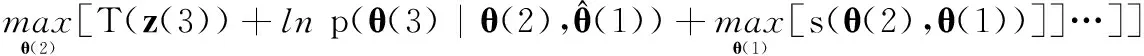
(10)
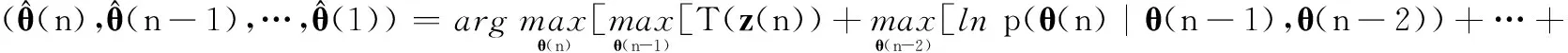
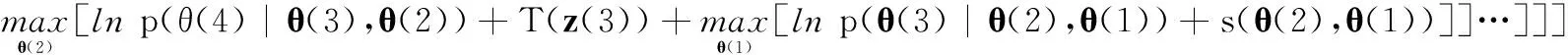
(11)
这样,将DP算法演变为一系列二维寻优的嵌套,通过考虑更多的状态关联可能性,以保证沿目标速度方向的评价函数更优。虽然这样做增加了算法的复杂度,却能提供比Pulford方法更好的对低SNR目标的检测能力。基于这种想法,我们提出了下述基于二阶Markov模型的改进DP算法。
2 改进的DP算法
2.1算法描述
改进算法采用与式(5)一样的评价函数,但不同的是,采用二阶Markov模型描述目标的运动,即
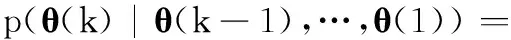

(12)
这样,评价函数变为下述递归形式,即
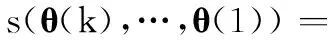
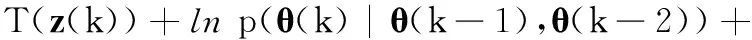
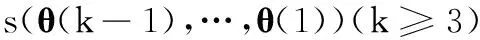
(13)
初值

将式(13)代入式(4)中,得到
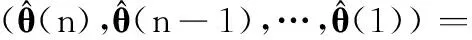

(14)
由式(14),对θ(k-2)寻优总会涉及到接下来两个时刻的状态θ(k)和θ(k-1)。因此,θ(k)和θ(k-1)可用来反推θ(k-2)以获得目标速度和位置。检测运动目标时,类似于上述Pulford方法,在推测位置周围搜索目标可使搜索范围更小,从而减小搜索区域内的噪声对寻优过程的干扰,使算法能够更好的检测运动目标。

2.2搜索区域设置
如前文所述,改进算法的重点在于利用速度对目标位置反推、并以推测点为中心设置搜索区域的过程。
与常规跟踪方法类似,对匀速直线运动的目标来说,反推目标位置可利用线性外推实现。若已知θ(k)及,θ(k-2)的外推点可表示为
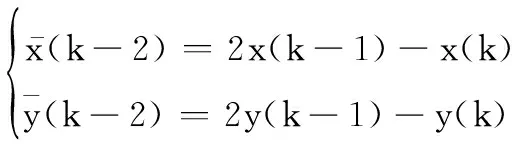
(15)
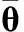
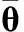

图3 θ(k-2)的改进搜索区域Fig.3 Search region of θ(k-2)
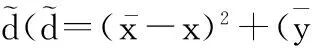
(16)
一般来说,外推精度越低,目标就越可能远离外推点,那么rI就要增大。工程中,我们可以给定一个漏检概率Pmiss,并将满足
(17)
的r的最小值作为rI。由于θ(k)在x,y方向上相对像元中心的误差不超过,故由式(15),相对在x,y方向的误差不超过,因此可取。这样,若假设Pmiss=0.01,则相对应的σI=Δ/2。
改进算法在搜索目标方面相比传统DP算法以及Tonissen、Pulford等方法的区别主要在以下两方面。

(2) 对Tonissen、Pulford等方法,目标的搜索范围与目标的历史轨迹有关。如前文所述,若目标的SNR低,历史轨迹就可能不准。这样,搜索范围虽得以缩小,却可能因对速度估计不准确而导致漏掉目标,影响评价函数沿目标轨迹的累积,降低算法对低SNR目标的检测性能。但对本文的改进算法来说,在减小搜索范围的同时,通过假设不同的目标速度,从而考虑更多目标状态转移的可能性,也就减少了漏掉目标的情况的发生,提高了对低SNR目标的检测性能。
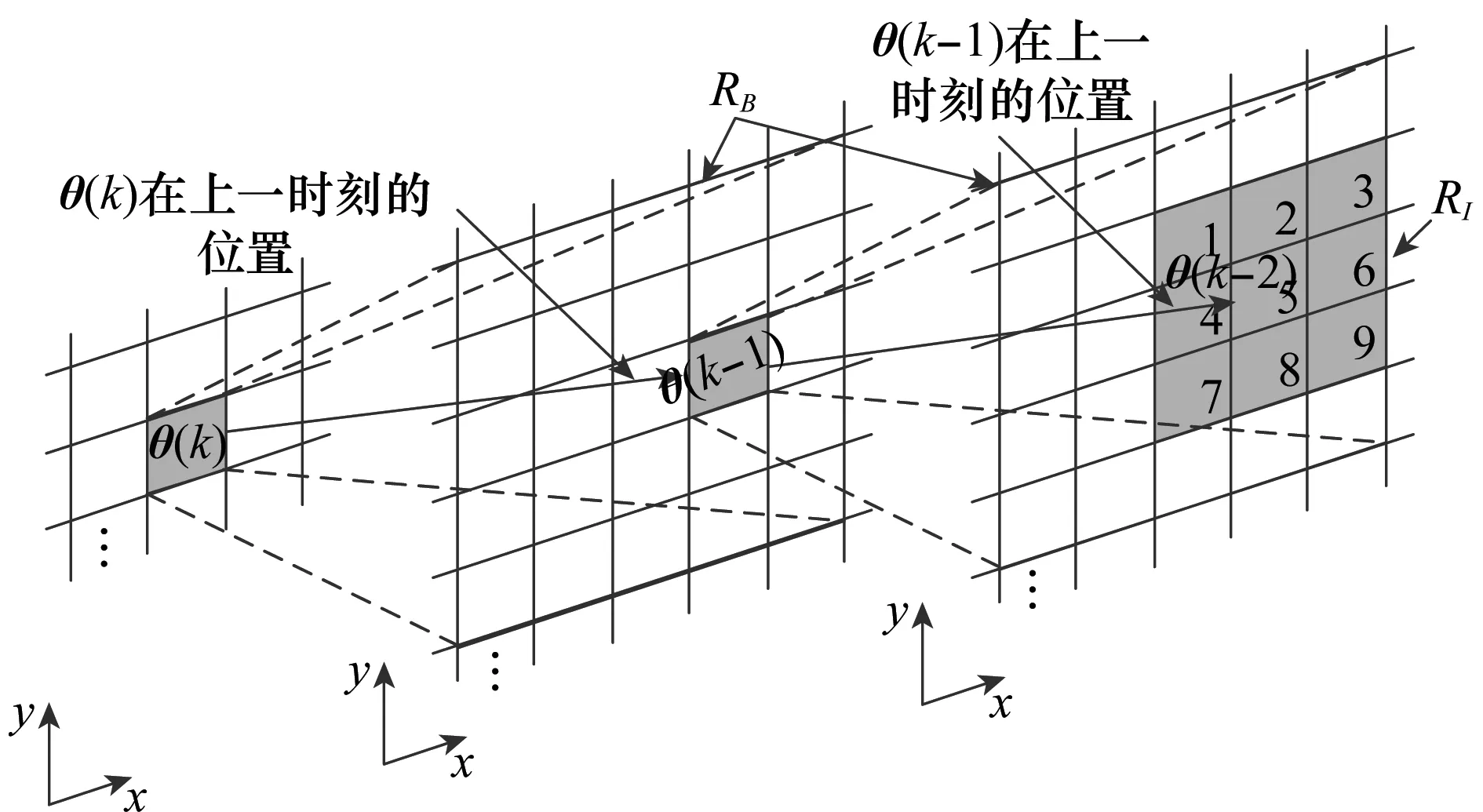
图4 搜索区域RB与RI的关系Fig.4 Relationship of search region RBand RI
2.3算法实现
至此,利用改进算法,低SNR的运动目标得以被有效检测。式(14)的计算过程可由下述步骤实现:
步骤 1k=3时,任给θ(3),以其为中心设置包含qB个像元的搜索区域RB,将θ(3)与RB中任意θ(2)关联,形成关联对(θ(3),θ(2));
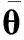
步骤 3重复步骤2,完成对RB中qB个θ(2)的遍历;

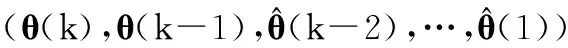
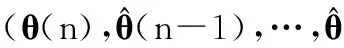
3 检测性能的分析
Barniv给出分析算法检测性能的方法[12]:先分别沿噪声和目标轨迹获得各自评价函数值的分布,然后将噪声和目标轨迹的评价函数值超过门限VT的概率分别定义为虚警概率PFA及检测概率PD,利用PFA及PD分析算法的检测性能。
可见,能否对算法的检测性能加以正确分析的关键在于是否能准确获得噪声和目标轨迹评价函数值的分布。下文我们分别给出Arnold的DP算法以及我们的改进算法的评价函数值分布的描述方法。
3.1Arnold的DP算法的评价函数值的分布
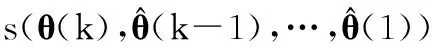
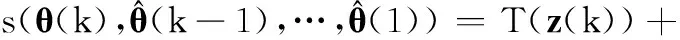
(18)
一般情况下,max[·]不是正态的,故评价函数值的分布函数很难准确得到[13]。为此,我们给出下面这种计算评价函数值分布的方法。
(19)
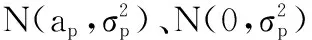
(20)
即T(z(k))的概率密度fz(x)可由测量z(k)的分布得到。
而对fmax(x;k-1),若假设max[·]中的qB个评价函数值独立同分布,则它们的最大值分布是它们各自分布的乘积[15],即
(21)
利用式(19)~式(21),评价函数值的分布可以递归得到,初值Fs(x;1)为T(z(1))的分布函数Fz(x)。
沿目标轨迹,类似有
(22)
其中
(23)
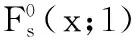
3.2改进DP算法的评价函数值的分布
接下来用类似的方法,研究改进DP算法的评价函数值的分布。
改进算法的寻优过程相比传统DP算法的复杂一些,为此,将式(14)中前n-1步寻优拆分为以下3个阶段:
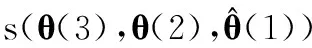
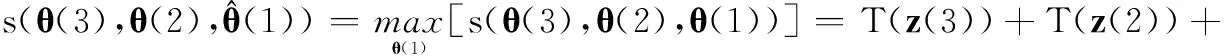

(24a)

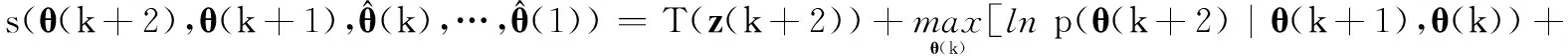
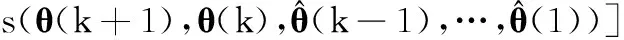
(24b)
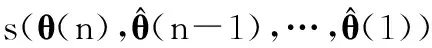
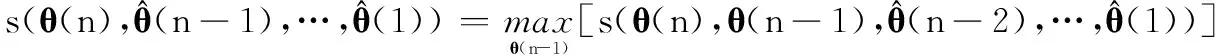
(24c)
式中各p(θ(k)|θ(k-1),θ(k-2))可按式(16)计算并归一化得到,下文简记为p1,…,pqI。
沿噪声轨迹,与式(24a)~式(24c)对应,各时刻评价函数值的分布可表示为
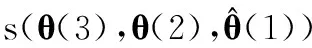
(25a)
式中,初值Fs(x;1)为T(z(1))的分布Fz(x)。
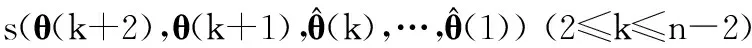
(25b)
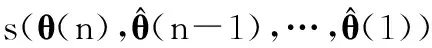
(25c)
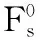
分别与式(24a)~式(24c)对应,各时刻评价函数值的分布可表示为
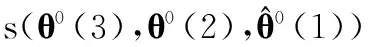
(26a)
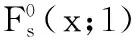
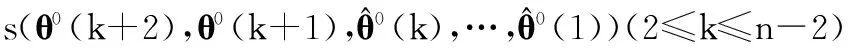
(26b)
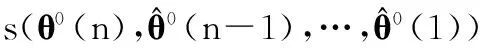
(26c)
3.3检测性能的分析
利用上面得到的评价函数值的分布,对改进算法的检测性能进行分析,并比较其与传统DP算法的差别。
按照对PFA及PD所下的定义,PFA及PD可表示为
(27)
(28)
分别利用由式(19)、式(21)及式(25)给出的Arnold及改进DP算法沿噪声轨迹评价函数值的分布,可以确定与给定虚警概率所对应的检测门限VT,再分别利用由式(22)、式(23)及式(26)给出的两算法沿目标轨迹评价函数值的分布,可以计算得到它们各自的检测概率。
定义目标的SNR为
SNR=a/σ
(29)
在噪声n(k)~N(0,1.52)、虚警概率PFA=0.01的条件下,对两种算法的检测性能加以分析比较。
图5给出了在qB=9及25、qI=9时,两种算法的检测概率PD与总检测帧数n的关系。比较图5(a)和图5(c)。虽qB=qI=9,即两种算法的搜索区域相同,但对相同检测帧数,改进算法的检测概率更高,即能更好的检测低SNR目标。换句话说,对同一目标,改进算法在达到相同检测概率时相比传统DP算法所需的检测帧数更少,即算法的检测效率更高。
此外,比较图5(b)和图5(d),随着目标搜索范围的扩大,相同帧数下改进算法的检测概率比传统DP算法的高很多。而且在分别比较与图5(a)~图5(d)后发现,改进算法的检测性能相对受目标搜索范围大小的影响更弱,故改进算法更适合于检测运动目标。
由上述对比可见,改进DP算法不仅可改善对低SNR运动目标的检测能力,还可缩短所需的检测帧数,实现了对运动目标更快、更准地检测效果。
4 算法仿真分析
我设计了下述仿真场景。传感器的分辨率为128×128,背景噪声n(k)~N(0,1.52)。目标做匀速直线运动,其帧间运动速度分别为1个像元和2个像元。对各DP算法,当目标帧间速度为1个像元时取RB为3×3像元,而当目标帧间速度为2个像元时取RB为5×5像元,RI取为3×3像元。对Pulford方法,将Rθ(k-1)取为3×3像元,Kalman滤波的初始速度由各轨迹前两帧状态经线性外推得到,目标帧间速度为1个像元时初始方差阵为E,帧间速度为2个像元时初始方差阵为4E,其中E为4×4的单位阵。检测门限为恒虚警门限,对应虚警概率PFA=0.01。
首先比较Arnold的DP算法、Pulford的DP算法以及本文的改进算法在检测SNR为1.6~2.5的目标时所需的检测帧数。我们对不同速度不同SNR的目标各做了100次仿真,并将各次检测结果的平均值定义为“平均检测帧数”。在每次仿真中,测量噪声及目标初始位置及速度方向随机。仿真结果示于图6,可以看出,相比Arnold方法,如果目标的速度较快,Pulford方法检测目标有明显的性能优势。但当目标速度慢时,Pulford方法检测SNR低于1.8的目标时所需的帧数却反多于Arnold方法,说明此时估计的“目标速度”不够准确,搜索范围有偏差,影响了检测性能。对改进算法,它的平均检测帧数是3种方法中最少的,且目标的SNR越低,与其他两种方法的差别越明显,证明了它检测低SNR运动目标的有效性。
(30)
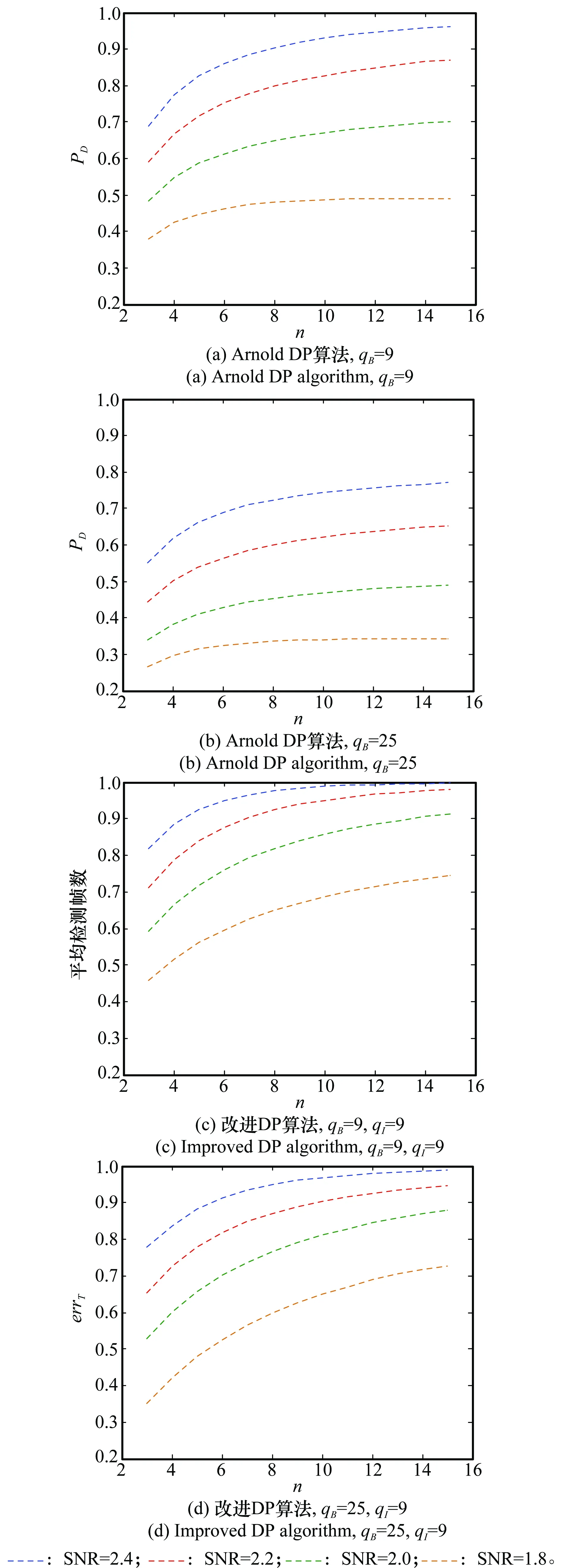
图5 算法检测概率与检测帧数的关系Fig.5 Relationship of detection probability and detection frame

图6 SNR与检测帧数的关系Fig.6 Relationship of SNR and detection frame
这里用errT衡量算法的跟踪精度。图7给出在n=40时,errT与SNR的关系。图中errT的数据是对各信噪比目标做100次仿真,并将结果取平均值得到的。每次仿真中,目标做匀速直线运动,测量噪声及目标初始位置及速度方向随机。可以看出,3种算法在SNR≥2.5时均能够较准确地跟踪目标。SNR<2.5时,随信噪比降低,3种DP方法的跟踪误差均逐渐开始增大。目标运动较快时,Pulford方法的误差始终小于Arnold方法,但若目标运动得慢,当SNR低于1.8,Pulford方法的误差反而超过了Arnold方法,再次证明目标SNR很低时Pulford方法对“目标速度”的错误估计会对检测结果产生负作用。相比而言,改进算法的跟踪误差最小,体现出对低SNR目标更好的跟踪性能。
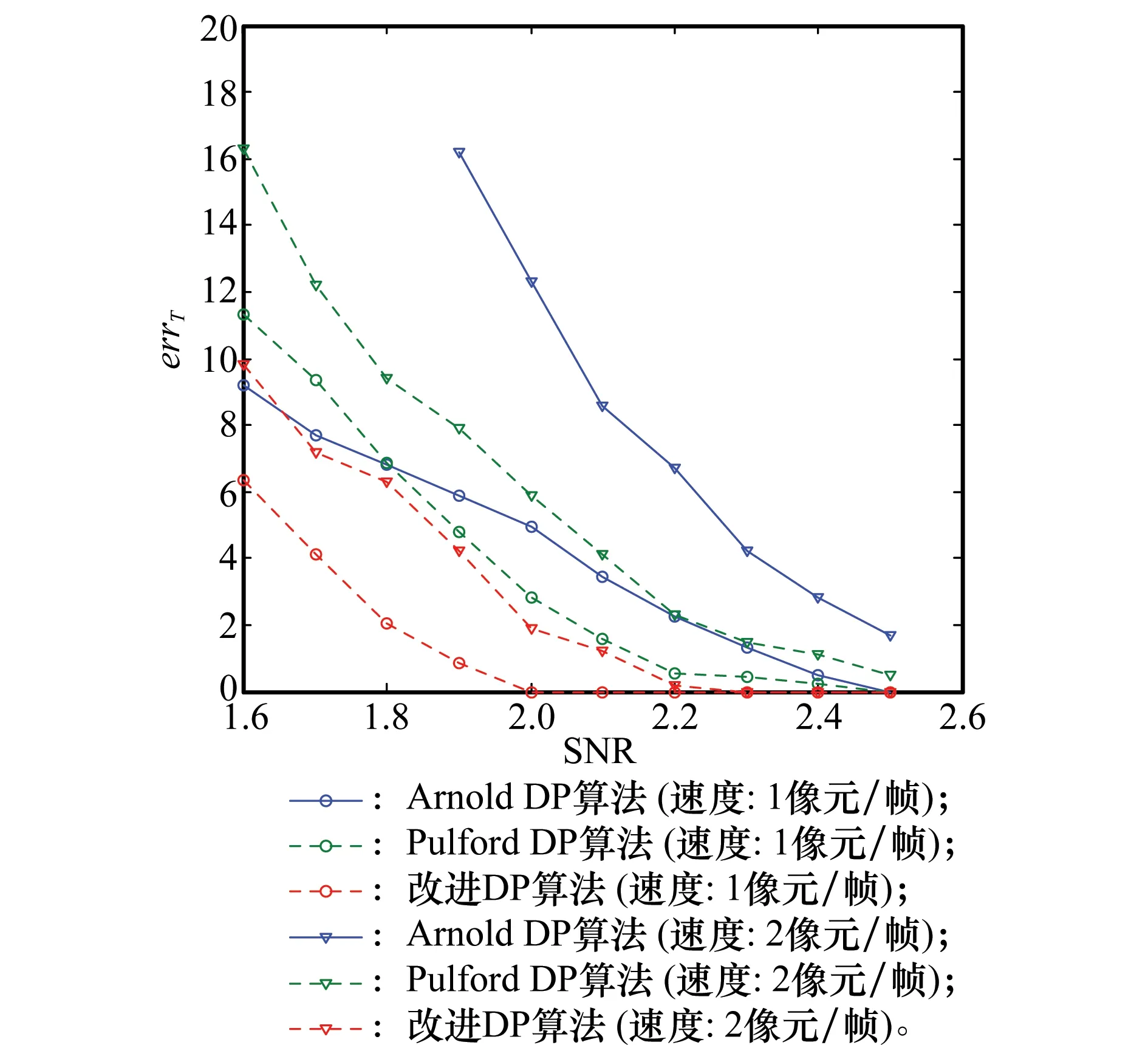
图7 SNR与跟踪误差的关系Fig.7 Relationship of SNR and tracking error
5 结 论
本文通过研究在检测运动目标时,传统DP算法的检测性能显著下降的原因,提出了基于二阶Markov模型的改进DP算法。改进算法在寻优过程中利用目标速度对目标位置进行反推,减小了搜索范围,从而减小了噪声对寻优过程的干扰。通过对算法性能的分析及仿真发现,改进算法具有很好的低SNR检测能力,同时提高了对运动目标的检测性能,在检测低SNR运动目标方面有一定优势。
[1]BellmanRE. Dynamic programming[M].Princeton:PrincetonUniversityPress, 1957.
[2]LarsonRE,PeschonJ.Adynamicprogrammingapproachtotrajectoryestimation[J].IEEE Trans.on Automatic Control, 1966, 11(3): 537-540.
[3]ViterbiAJ.Convolutionalcodesandtheirperformanceincommunicationsystems[J].IEEE Trans.on Communication Technology, 1971, 19(5): 751-772.
[4]BarnivY.Dynamicprogrammingsolutionfordetectingdimmovingtargets[J].IEEE Trans.on Aerospace and Electronic Systems, 1985, 21(1), 144-156.
[5]ArnoldJ,ShawS,PasternackH.Efficienttargettrackingusingdynamicprogramming[J].IEEE Trans.on Aerospace and Electronic Systems, 1993, 29(1), 44-56.
[6]TonissenSM,EvansRJ.Performanceofdynamicprogrammingtechniquesfortrack-before-detect[J].IEEE Trans.on Aerospace and Electronic Systems, 1996, 32(4), 1440-1451.
[7]PulfordGW,LaScalaBF.Multihypothesisviterbidataassociation:algorithmdevelopmentandassessment[J].IEEE Trans.on Aerospace and Electronic Systems, 2010, 46(2): 583-609.
[8]LuoXY,LiX.ZuoL,etal.Radarweaktargetdetectionbasedondynamicprogramming[J].Systems Engineering and Electronics,2011,33(7):1491-1496.(罗小云,李响,左磊,等.基于动态规划的雷达微弱目标检测[J].系统工程与电子技术,2011,33(7):1491-1496.)
[9]HuL,WangSY,WanY.ImprovedTBDalgorithmbasedondynamicprogramming[J].Journal of Air Force Radar Academy,2010,24(2):79-82.(胡林,王首勇,万洋,等.基于动态规划的TBD改进算法[J].空军雷达学院学报,2010,24(2):79-82.)
[10]CaoQ,WangDJ,ZhangQ,etal.Energyaccumulationininfraredpointtargetdetection[J].Optics and Precision Engineering,2010,18(3):741-747.(曹琦,王德江,张齐,等.红外点目标检测中的能量累积[J].光学精密工程,2010,18(3):741-747.)
[11]ZhengDK,WangSY,YangJ,etal.Amulti-frameassociationdynamicprogrammingtrack-before-detectalgorithmbasedonsecondorderMarkovtargetstatemodel[J].Journal of Electronics and Information Technology, 2012, 34(4): 885-890. (郑岱堃, 王守勇, 杨军, 等. 一种基于二阶Markov目标状态模型的多帧关联动态规划检测前跟踪算法[J].电子与信息学报, 2012, 34(4): 885-890.)
[12]BarnivY,KellaO.DynamicprogrammingsolutionfordetectingdimmovingtargetspartII:analysis[J].IEEE Trans.on Aerospace and Electronic Systems, 1987, 23(6), 776-788.
[13]JohnstonLA,KrishnamurthyV.Performanceanalysisofadynamicprogrammingtrackbeforedetectalgorithm[J].IEEE Trans.on Aerospace and Electronic Systems, 2002, 38(1), 228-242.
[14]PapoulisA. Probability, random variables, and stochastic processes[M].NewYork:McGraw-Hill, 1965.
[15]LawlessJF. Statistical models and methods for lifetime data[M].NewYork:Wiley, 1982.
Improved dynamic programming algorithm for low signal-to-noise ratio moving target detection
WANG Shuo, ZHANG Yi-qun
(Beijing Institute of Electronic System Engineering, Beijing 100854, China)
The dynamic programming (DP) algorithm for detecting dim targets is investigated. Due to the poor performance of detecting dim moving targets with traditional DP, an improved DP algorithm is proposed. The algorithm models the process of target state transition with a second-order Markov model, and on this basis transfers the optimization of traditional DP to a series of 2-dimensional optimizations. Thus, the target search region of the improved algorithm is narrowed on condition of considering a variety of target velocities, and the detection performance of dim moving targets for the DP algorithm is improved.
dynamic programming (DP); second-order Markov model; low signal-to-noise ratio; moving point target; detection
2015-04-02;
2016-03-04;网络优先出版日期:2016-06-07。
TN 911.73
A
10.3969/j.issn.1001-506X.2016.10.04
王硕(1987-),男,博士,主要研究方向为目标检测与识别。
E-mail:daniel-ws@163.com张奕群(1962-),男,研究员,博士,主要研究方向为导航、制导与控制。
E-mail:yiqunzhang@hotmail.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160607.1605.014.html
