基于模型类型匹配PHD滤波器和TBM的多目标联合跟踪分类
2016-10-18赵天衢于耀中
詹 锟, 蒋 宏, 赵天衢, 于耀中
(北京航空航天大学自动化科学与电气工程学院, 北京 100191)
基于模型类型匹配PHD滤波器和TBM的多目标联合跟踪分类
詹锟, 蒋宏, 赵天衢, 于耀中
(北京航空航天大学自动化科学与电气工程学院, 北京 100191)
为了解决杂波和漏检下多目标的联合跟踪与分类问题,提出了模型类型匹配概率假设密度(probability hypothesis density,PHD)滤波器,同时将其与多传感器的可转移信度模型(transferable belief model,TBM)框架相结合,并用多个运动学雷达和粒子滤波递推实现。该算法对飞行器的先验信息进行估计,从而替代了属性传感器。在预测阶段,根据模型和类型对PHD滤波器进行粒子匹配;传感器得到观测结果后进行粒子权重的更新;再根据粒子对应的权重得到目标的后验状态-模型-类型分布;这些PHD滤波器可以同时得到目标的状态和类型;结合TBM和航迹粒子标签算法,得到多个传感器的融合结果。仿真表明,本文提出的模型类型匹配PHD滤波器的性能比传统多模型PHD滤波器更精确,同时多传感器的TBM框架也全面提升了算法的性能。
联合跟踪与分类; 概率假设密度; 可转移信度模型; 粒子滤波; 多传感器数据融合
0 引 言
在现代战争军事侦察系统中,多目标的跟踪与分类问题已经成为了最重要的两个技术难题。尽管这两个问题是耦合的,但是以往人们通常将它们用不同的传感器分别处理,用运动学传感器进行目标跟踪,用属性传感器进行目标分类。由于目标类型信息能够确定目标运动学包络,提高目标跟踪精度,而目标状态信息也有助于目标分类,因此这两类问题可以被放在统一的框架内进行处理,即联合跟踪与分类(joint tracking and classification,JTC)技术[1-2]。
通常,在进行多目标跟踪时,目标数量和目标状态都会随着时间而变化,并且还存在雷达的虚警、漏检等问题。传统的多目标跟踪算法主要有联合概率数据关联(joint probability data association,JPDA)和多假设跟踪(multiple hypothesis tracking,MHT)算法等。在目标数目变化和杂波漏检等情况下,这些传统的方法存在自身的不足,比如通常需要假定目标数目已知或者未知恒定,再通过数据关联进行滤波,使得实时性较差。为了克服这些困难,Mahler提出了基于有限集统计学 (finite set statistics,FISST)的概率假设密度(probability hypothesis density,PHD)滤波器[3-4]。
近些年,一些文献已经阐述了多目标的联合跟踪与分类问题。当观测结果在杂波干扰和雷达漏检等不利状况下,多目标联合跟踪与分类算法需要准确估计目标数量,目标状态和目标类型。传统的多目标跟踪算法(JPDA, MHT等)主要是基于观测到轨迹的关联技术,将每个观测结果与特定目标进行关联,再采用单目标的方法进行估计。当观测结果的数据量增加时,建立的观测到目标的组合关系呈几何式增长,数据关联将会占用多目标跟踪算法中大部分计算量,实时性差不利于工程实践。而近些年发展的PHD滤波器则是一个更好的多目标跟踪方法。该方法可以估计目标数量并省去了目标关联的计算,大大提高了时效性。PHD滤波器可以用序贯蒙特卡罗方法或者高斯混合方法来实现[5-7]。文献[8]基于Mahler的PHD滤波器提出了多目标跟踪与分类技术的方法,但存在许多缺点,如仅采用了一个PHD滤波器导致粒子不能根据类型概率进行转移,从而导致分类不准确和跟踪不精确。文献[9]提出了多目标的联合检测、跟踪与分类技术,该文献推导了类型匹配的PHD滤波器,改善了分类结果。本文在此基础上针对多目标高机动的情况,提出了模型类型匹配PHD滤波器(model-class-matched PHD filter)算法,能有效解决多机动目标的联合跟踪和分类。
另外,为了得到高精度和强鲁棒的跟踪器和分类器,还需要将多个传感器的观测结果进行数据融合。对于目标分类和多传感器数据融合问题,目前主要有两种使用较广泛的统计学方法,即贝叶斯方法和Dempster-Shafer (D-S)证据理论。其中,D-S证据理论可以看作是贝叶斯概率方法的推广,在处理不完全和不确定证据问题方面,有更强的鲁棒性[10]。对于雷达监视系统的目标分类问题,文献[11]分别采用贝叶斯方法和D-S证据理论进行了详细比较。结果证明,两种方法均得到了很好的分类结果,但是D-S证据方法对噪声和不确定的先验信息有更强的鲁棒性。Smets在基于D-S证据信度理论上推广出了可转移信度模型(transferable belief model,TBM),用以解决多传感器冲突的数据融合问题[12-13]。Smets提出了一种基于TBM框架的单目标联合跟踪与分类算法,该方法在目标分类方面比传统的贝叶斯分类器有更好的结果。文献[11]提出了一种基于TBM框架下的多传感器联合跟踪与分类技术,采用了Rao-Blackwellised粒子滤波和数据关联解决多目标问题。该方法的主要问题在于需要提前获得目标数目的信息,而且在观测结果较多时计算量会急剧增大。
本文将结合JTC技术与TBM框架来解决多目标多传感器问题,提出了基于模型类型匹配PHD滤波器联合跟踪分类算法(model-class-matched PHD Filer)并用序贯蒙特卡罗方法实现,同时用TBM方法来处理多传感器信息以得到更可靠的分类结果。全文主要由以下几个部分组成:第1节阐述了目标运动模型,观测模型和PHD滤波器的数学基础,并推导了模型类型匹配PHD滤波器算法;第2节建立了TBM框架以及基于粒子标记的航迹维持算法;第3节给出了基于序贯蒙特卡罗算法的伪代码;第4节给出了仿真实例并对结果进行分析;最后对全文进行总结。
1 多目标的联合跟踪与分类技术
本节详细阐述采用PHD滤波器来解决多目标跟踪问题以克服传统方法的弊端,同时给出了在JTC框架下的PHD滤波器的数学推导。
1.1有限集统计学原理和PHD滤波器
PHD滤波器解决多目标问题需要用到FISST理论来构建多目标后验概率密度函数[7, 14]。定义两个随机有限集分别来描述k时刻的多目标状态集Xk和测量集Zk。
(1)
式中,M(k)和N(k)表示k时刻的目标数和观测数,由于雷达观测存在虚警和漏检,因此M(k)可能不等于N(k)。
考虑如下3种目标变化的情况:新生目标、衍生目标和存活目标。多目标运动模型和雷达观测模型可以通过式(2)和式(3)来表述。给定k-1时刻的多目标状态随机有限集Xk-1,k时刻的多目标状态随机有限集Xk可以通过合并存活目标、衍生目标和新生目标的随机有限集得到,即
(2)
式中,Sk|k-1(Xk-1)表示k时刻存活目标的随机有限集;Bk|k-1(Xk-1)表示由Xk-1衍生目标的随机有限集;Γk表示k时刻新生目标的随机有限集。类似地,多目标观测随机有限集Zk可由下式得到。
(3)
式中,Θk(Xk)表示由多目标状态Xk生成的观测随机有限集;Κk表示杂波、虚警等产生的随机有限集。多目标跟踪问题就是已知时刻1~时刻k的观测集合Z1∶k={Z1,Z2,…,Zk}下,估计多目标状态Xk。
在FISST中,PHD也被称为强度,可以理解为多目标后验密度的一阶矩,其峰值可以用来估计多目标的状态。通过迭代Dk|k(·|Z1∶k)可以得到PHD滤波器,其中包含预测和更新两个步骤。
(4)
(5)
其中
(6)
式(4)为预测阶段:k-1时刻的目标状态xk-1依概率pS(xk-1)存活在k时刻;k时刻的衍生目标以概率βk|k-1(xk|xk-1)产生;新生目标以概率γk(xk)在雷达观测范围内生成; fk|k-1(xk|xk-1)为单目标的马尔可夫转移函数。
式(5)为更新阶段:在一些假设下,预测强度能通过观测Zk更新。这里假设:雷达虚警为泊松分布,其平均值为λk;噪声强度为Kk(zk);k时刻目标状态xk的检测概率为pD(xk);gk(zk|xk)为单目标测量似然函数。
多个目标的状态可以通过更新后的PHD峰值估计出来。通过式(4)和式(5)的迭代计算,PHD滤波器避免数据关联解决了多目标跟踪问题。
1.2JTC框架下的模型类型匹配PHD滤波器
JTC的基本条件是观测传感器能同时获取目标状态和目标属性的测量信息。本文仅采用带有先验飞行包络信息的运动学观测器和提出的基于模型和类型匹配的PHD滤波器来进行目标分类以代替属性传感器。比较传统的PHD滤波器,本文提出的PHD滤波器在跟踪和分类机动多目标时有更大的优势。
常规的多模型方法通过并行计算有限个滤波器来检测目标机动和识别模型。考虑计算复杂度和算法性能,交互式多模型(interactivemulti-tudemodel,IMM)算法是已知最有效的多模型方法。本文提出的模型匹配算法与IMM算法有相似的结构,尤其是在混合与融合两个阶段[15]。但是,本文提出的滤波器是跟踪机动目标和缩减分类范围并且状态后验概率密度也不一定是高斯的,所以IMM算法并不能直接用在本文提出的模型匹配算法上。因此本文采用多个并行PHD滤波器的模型匹配算法,能很好地处理多模型目标状态。
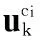
(7)
用Dk|k(xk,ci|Z1∶k)表示k时刻JTC框架下PHD滤波器的类型-状态的强度。本小节提出一个递归的多目标联合跟踪与分类算法,使用了基于模型和类型匹配的PHD滤波器,具体描述如下所示:
(1) 混合阶段
(8)
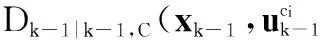
(2) 预测阶段
(9)
式中
(10)
新生目标概率γk,C(·),存活概率pS,C(·)和衍生目标概率βk|k-1,C(·)都是模型类型依赖,而pβ,k/k-1(·)为类型转移概率。
(3) 更新阶段
通过时刻k获得的测量值Zk,更新PHD可以由式(11)计算:
(11)
式中
(12)
式中,pD,C(·)表示状态和类型依赖的目标检测概率;gk,C(·)表示基于模型和类型的单目标观测似然,其中包含了动力学和属性信息;Kk(·)与式(5)中的含义相同。
(4) 融合阶段
本文的滤波器并不需要得到更新后的每个模型概率,因为基于模型和类型匹配的PHD将作为一个整体用在下一个混合阶段中。该滤波器的目的只是估计出目标状态而不是预测其每一时刻的运动模型。
更新后的目标估计总数为
(13)
k时刻的整体后验PHD为
(14)
多目标的状态可以通过提取整体后验PHD的Nk个(对Nk|k四舍五入)局部最大值得到。
本文提出的模型类型匹配PHD滤波器由以上4个步骤组成,其算法结构如图1所示。
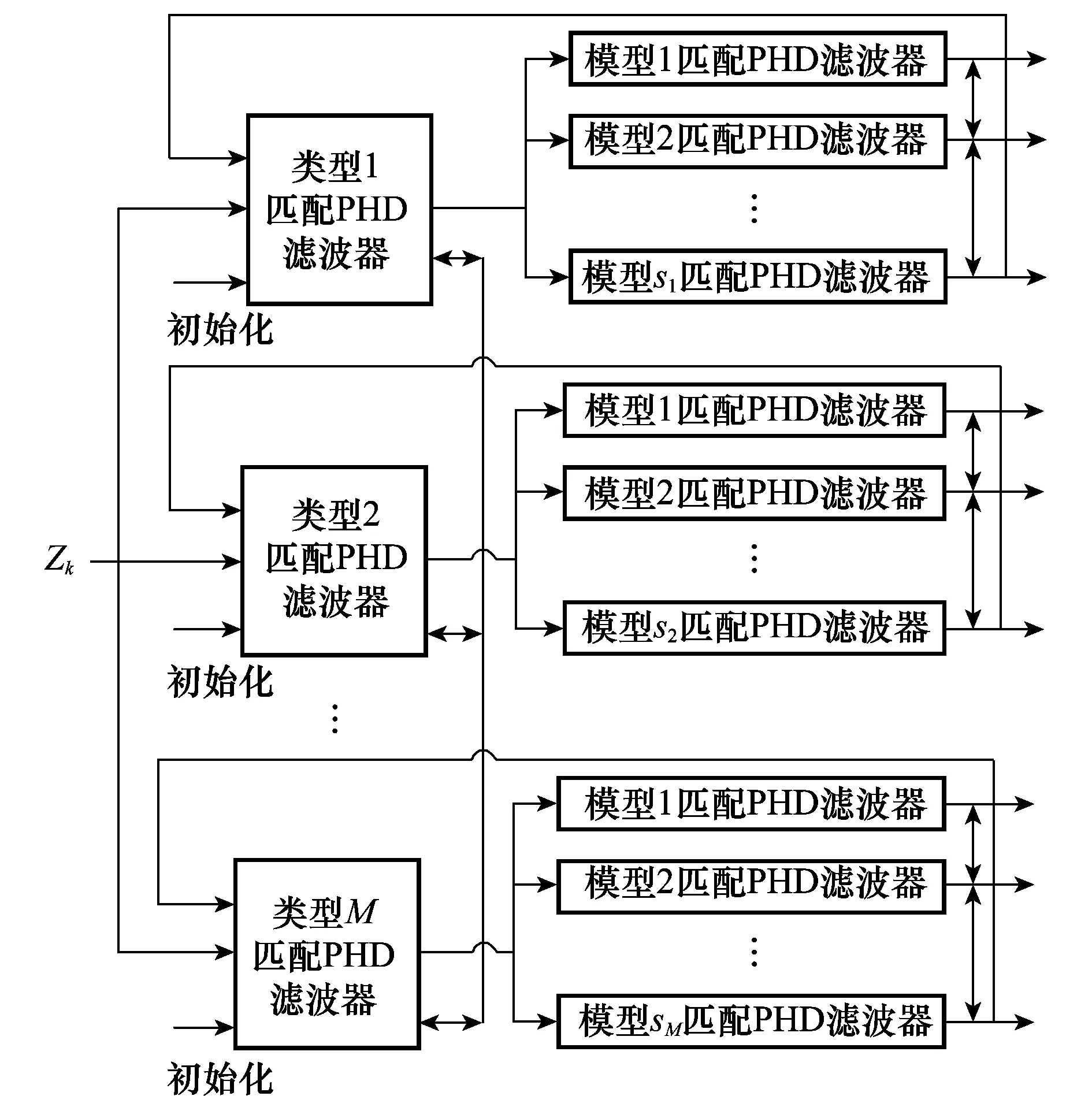
图1 模型类型匹配PHD滤波器的结构Fig.1 Structure of model-class-matched PHD filter
2 多传感器融合与航迹关联技术
现代战争中,单个雷达传感器已经不能满足跟踪和识别的精确性和鲁棒性要求了,因此需要具有高容错的多传感器融合系统。贝叶斯方法和D-S证据理论是广泛使用的两种目标识别方法。D-S证据理论可以用来解决不完全和不确定性证据下的判别问题,而贝叶斯方法不行。为此,本文将在多传感器系统中采用JTC框架下的模型类型匹配PHD滤波器,并结合D-S方法来识别目标;同时,采用贝叶斯方法来估计目标状态;另外,为了分别得到各个目标的运动轨迹和目标的类型概率,还需要采用航迹维持算法。
2.1可转移信度模型
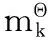
(15)
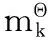
(16)
TBM框架分为两部分:Credal层和Pignistic层。在Credal层,信度被分配到各自的事件集合中,并被不断更新;再利用Pignistic函数对来自Credal层的信度进行变换,得到Pignistic概率。通过这个概率可以做出最优决策。
为了将证据理论与PHD滤波器结合,目标的分类结果必须通过不同的信号源融合来进行修正。来自多个传感器的信度可以通过Dempster融合准则进行融合:
(17)
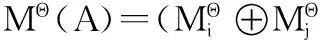
为了得到能辅助决策的概率分布,需要给MΘ(A)中的单命题x∈A⊆Θ分配概率。因此,对于每个单命题x,可以利用Pignistic概率分布BetP得到:
(18)
式中,|A|表示Θ中单命题的数量。在目标分类阶段,每一时刻计算出Pignistic概率,即得到目标的类型概率。表1给出了多传感器TBM算法。

表1 多传感器TBM融合算法
2.2航迹维持算法
传统PHD滤波器无法形成每个目标的跟踪航迹,对后续分析(目标分类和态势估计等)造成了不便,因此需要把目标状态估计与目标航迹关联起来。本文的航迹关联采用粒子标签法[17-18]:该方法能够识别雷达观测值之间的同一目标,并进行航迹关联,还可以一定程度上滤除杂波。
粒子标签法的主要思想为:在PHD滤波器的每次迭代中,先对每个粒子按照目标的状态 (位置和速度)进行划分,并给相同划分中的粒子赋予相同的标签;重采样时,将父粒子的标签传递给采样后的子粒子;重采样后,再对粒子进行聚类,将一个类中拥有相同标签且占主要的粒子,与上一时刻的类相关联;最终,将具有相同标签的目标关联起来,即为每个目标的完整航迹。
本文提出的多传感器融合算法需两次使用粒子标签法,分别用在单传感器的航迹关联和多传感器融合的航迹关联,如表2和表3所示。

表2 单传感器的粒子标签关联算法

表3 多传感器的粒子标签关联算法
3 蒙特卡罗算法实现
本文采用序贯蒙特卡罗方法来实现多传感器模型类型匹配PHD滤波器,算法步骤如下。
步骤 1初始化阶段

步骤 2预测阶段
对于现存目标和衍生目标,i=1,2,…,Lk-1:
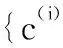
对于新生目标,i=Lk-1+1,…,Lk-1+Jk:
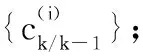
步骤 3更新阶段
对于zk∈Zk,计算:
权重更新为
步骤 4重采样阶段

步骤 5状态估计阶段
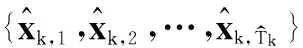
步骤 6轨迹关联阶段
利用表2的方法进行目标轨迹关联。
步骤 7类型估计阶段
计算每个目标的类型概率:
用{Pr1(c),Pr2(c),…,Prm(c)}表示多传感器对某目标关于c类型概率的集合,m为传感器的总数。
步骤 8多传感器融合阶段
将所有传感器的状态估计合并,定义一个关联候选集合:
按照如下步骤将不同传感器的估计关联:
用表1算法计算多传感器融合后每个目标的状态和分类概率。
用表3算法计算得到多传感器融合后每个目标的航迹。
4 仿真与分析
4.1系统模型
本文建立了一个二维平面的机动目标模型,由CV模型加上机动输入组成。其动力学方程如下:
(19)
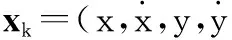
(20)
系统在k时刻的观测模型如下:
(21)
式中,观测函数h(·)为非线性模型,测量噪声服从高斯白噪声,即vk~N(0,R)。
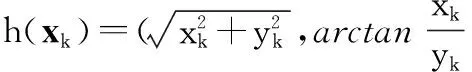
4.2仿真实例
我们建立了一个实战的仿真事例,此场景是在一个[-20 000m30 000m]×[-20 000m10 000m]的二维平面上。假设雷达的采样时间为T=1s,总仿真步长为200s。最开始,场景内有一架无人机在进行侦查,假定为目标1;100s后,有一个目标2(战斗机)以匀速飞入场景内;在150s时,该战斗机发射了一枚导弹,即目标3。无人机的初始状态为[-8 000m, 0m/s, 8 000m,-200m/s],战斗机的初始状态为[-18 500m, 400m/s,-10 000m, 50m/s],其发射的导弹的初始状态为战斗机在150s时的状态。目标1在71~73s和101~103s以[2 g, 2 g]的加速度机动。目标3在151s以[5 g5 g]做了3s的高机动。其他时刻,这些目标均以匀速进行运动。其真实运动轨迹和雷达位置如图2所示,其中I表示起始点,F表示终止点。
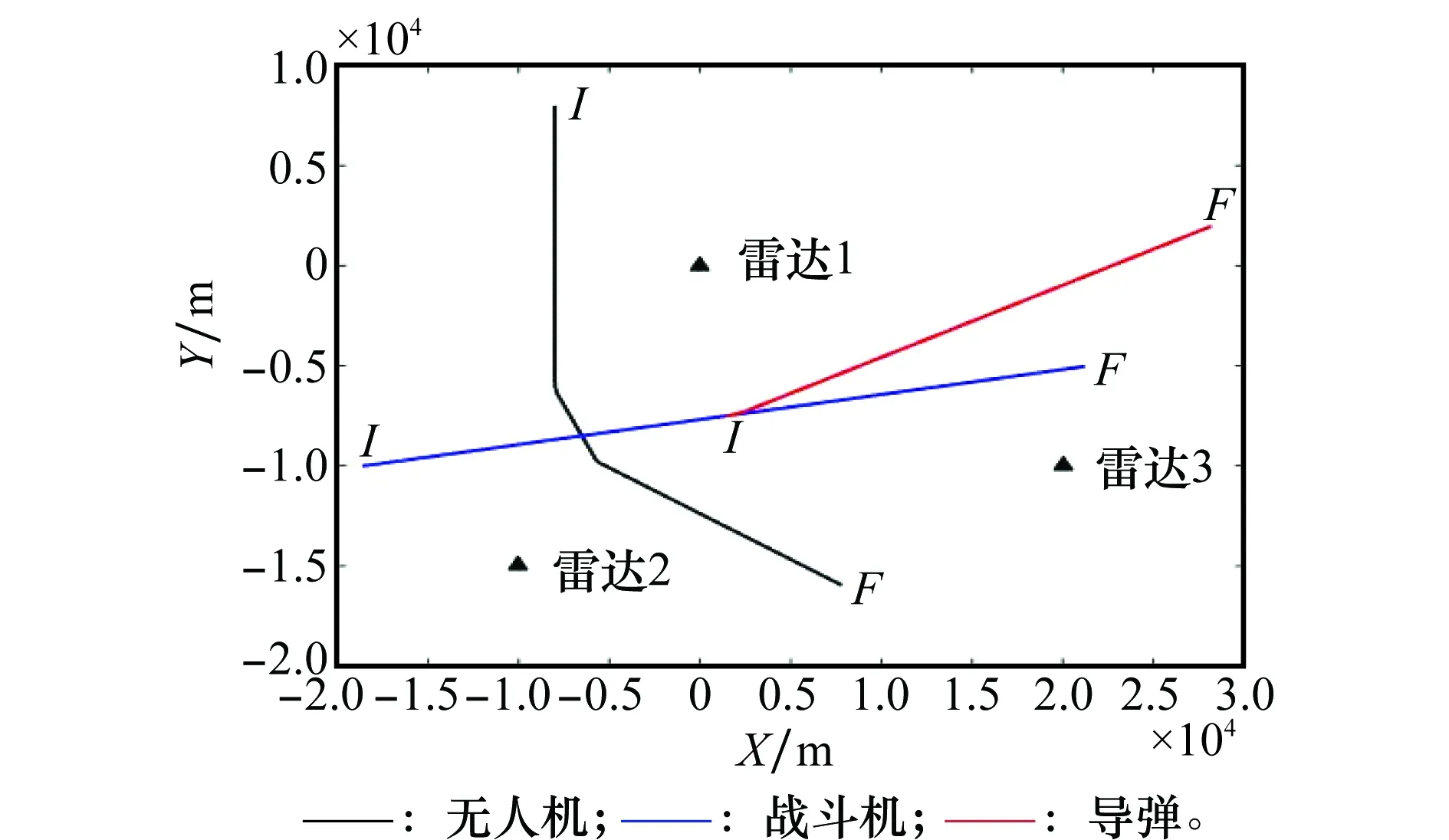
图2 目标真实运动轨迹和观测雷达位置Fig.2 Targets’ true trajectories and radar positions
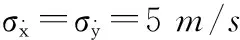
本文有3种目标类型:无人机、战斗机和导弹,用目标的速度似然函数来代替属性传感器,提供目标分类的信息,其速度似然函数如图3所示。
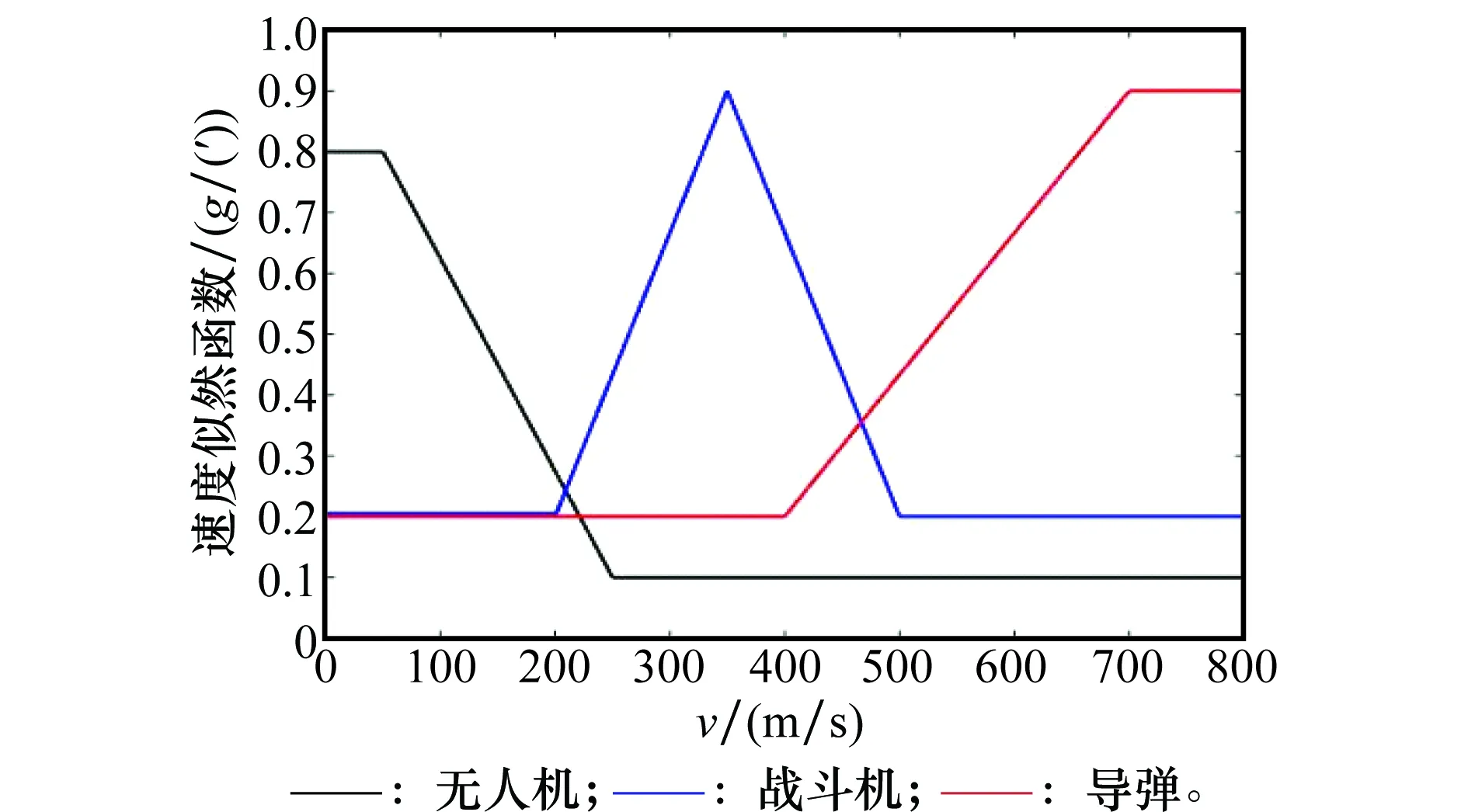
图3 速度似然函数Fig.3 Speed likelihood function
对于不同类型的目标,假设其机动输入uk为5个跳变状态的马尔可夫过程,即
(22)
其中,战斗机和导弹对应的加速度:A=5 g;无人机的加速度:A=2 g。
模型马尔可夫转移矩阵为
(23)

γk,C=0.05N(·;[-18 500,400,-10 000,0]T,
diag([100,50,100,50]))
粒子滤波中的粒子数量根据估计目标数自适应得到。对每个估计的目标分配1 000个粒子,即Nparticle=1000。初始化时每个目标分配500个粒子,每个新生目标分配500个粒子。
将本文提出的多目标多传感器滤波算法与传统多模型PHD滤波器和单传感器模型类型匹配PHD滤波器进行比较。为了有效评价算法优劣,本文采用最优子模式分配(optimalsubpatternassignment,OSPA)距离[19-20]来比较估计误差。重复进行了100次仿真试验并取平均值后,得到图4。该图给出了不同滤波算法的目标位置和目标数目的估计结果。比较图4(a)和图4(b),无论目标位置估计或是目标数量估计,单传感器模型类型匹配PHD滤波器比传统多模型PHD滤波器更精确,特别是在目标衍生阶段。这是由于目标类型信息帮助缩小了目标机动范围的估计,因而提高了滤波器的估计精度。而从图4(c)可以看出,多传感器模型类型匹配PHD滤波器能进一步提高估计精度,因为多个雷达能最大程度消除漏检问题,同时TBM框架也解决了多雷达冲突情况。
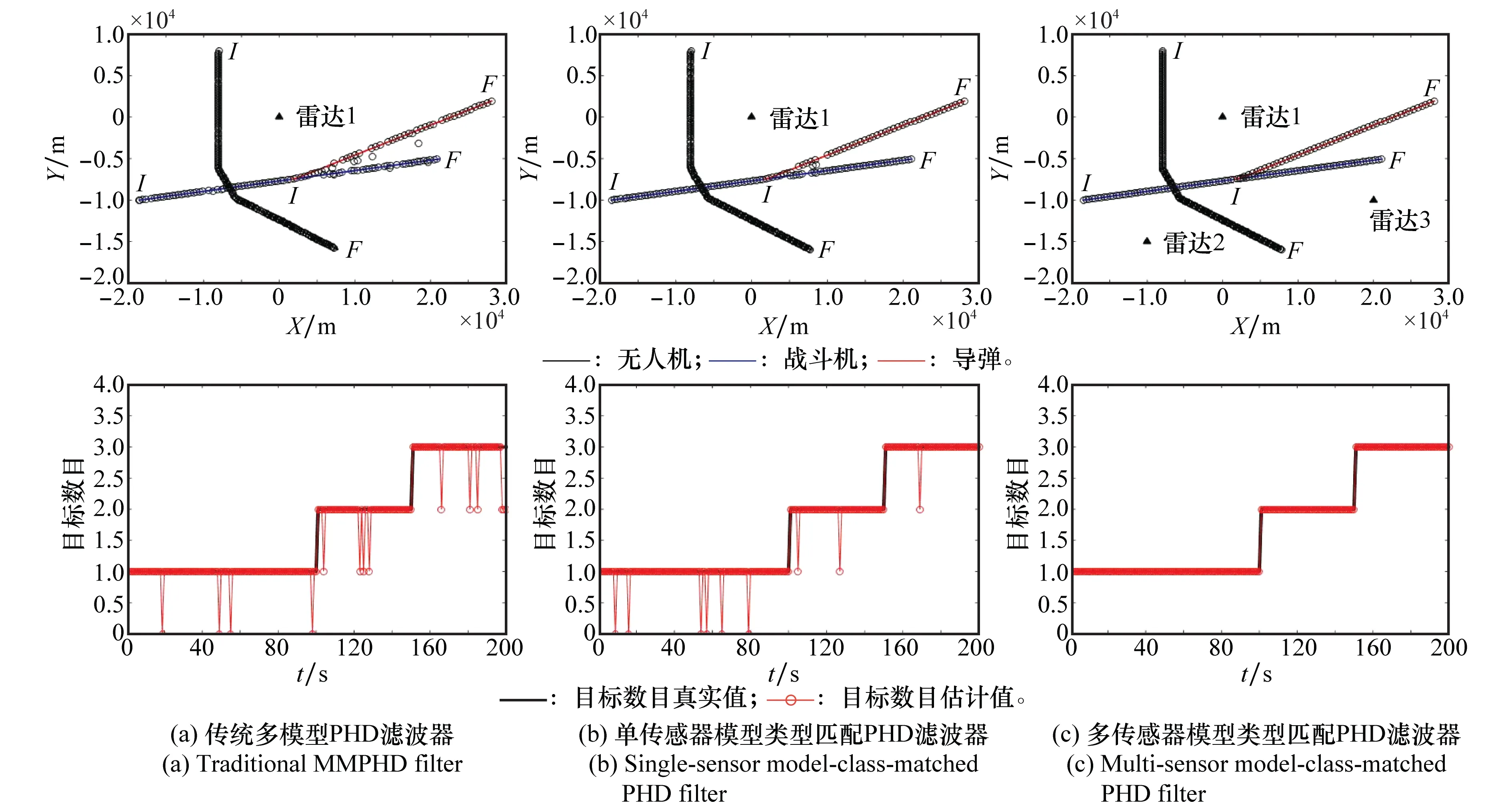
图4 3种算法的目标位置和目标数量估计Fig.4 Estimation of target position and number by three methods
利用OSPA距离计算真实轨迹与估计轨迹的偏差量,其中OSPA参数选取为p=2和c=5000,结果如图5所示。可以看到,单传感器模型类型匹配PHD滤波器比传统多模型PHD算法的误差更小,且更平稳。当产生衍生目标时,传统多模型滤波算法不能很好地分辨出目标的状态和数目。与此同时,多传感器模型类型匹配PHD滤波器相比单传感器算法而言,其误差又进一步减少,同时目标数目的估计非常准确。这是由于多传感器消除了单传感器观测漏检的问题,因而多传感器算法对于目标检测、目标衍生以及目标高机动都有很好的鲁棒性。

图5 OSPA距离Fig.5 OSPA distance
图6表明,基于TBM框架的多传感器融合技术的目标分类结果明显好于单传感器算法的分类结果。在单传感器分类算法中,新生和衍生的目标对于分类结果造成了较大影响。从图6(b)可以看到,多传感器分类算法对于多目标情况有较快的分类速度,这对于战场的势态分析是十分重要的。这主要是因为多传感器克服了单传感器观测结果的不确定性并提供了一个可靠的融合结果。
同时,为了比较算法的复杂性,本文做了如下复杂性测试:运行100次算法后,传统多模型PHD的平均计算时间为120.8s;模型类型匹配PHD-JTC为186.4s;多雷达模型类型匹配PHD-JTC为207.8s。

图6 两种算法的目标分类结果Fig.6 Classification results of two algorithms
5 结 论
本文提出一个有效的多目标多传感器联合跟踪分类算法。该算法基于模型类型匹配PHD滤波算法和TBM融合框架。仿真中仅使用了运动学传感器并利用目标先验信息来实现目标分类。仿真结果表明:本文提出的多传感器模型类型匹配PHD滤波器比传统的多模型PHD滤波器在目标数目和OSPA距离估计上都有更高的精确度;同时多传感器融合的结果则比单传感器的结果更好。提出的该算法主要有两大优势:能够同时估计目标数目,目标状态和目标类型;使用TBM框架能很方便地扩展到多种传感器领域,不管观测器得到的是属性信息还是运动学信息。今后的工作可以考虑将刚体模型加入到该滤波算法中来,提高目标的属性识别能力。
[1]MillerMI,SrivastavaA,GrenanderzU.Conditional-meanestimationviajump-diffusionprocessesinmultipletargettracking/recognition[J].IEEE Trans.on Signal Processing,1995,43(11):2678-2690.
[2]ChallaS,PulfordGW.Jointtargettrackingandclassificationusingradarandesmsensors[J].IEEE Trans.on Aerospace and Electronic Systems, 2001,37(3):1039-1055.
[3]MahlerRP.MultitargetBayesfilteringviafirst-ordermultitargetmoments[J].IEEE Trans.on Aerospace and Electronic Systems, 2003,39(4):1152-1178.
[4]Ba-NguV,Wing-KinM.Aclosed-formsolutionfortheprobabilityhypothesisdensityfilter[C]∥Proc.of the 8th International Conference on Information Fusion, 2005: 556-570.
[5]LinL,Bar-ShalomY,KirubarajanT.TracklabelingandPHDfilterformultitargettracking[J].IEEE Trans.on Aerospace and Electronic Systems, 2006,42(3):778-795.
[6]HueC,LeCadreJP,PerezP.PosteriorCramer-Raoboundsformulti-targettracking[J].IEEE Trans.on Aerospace and Electronic Systems, 2006,42(1):37-49.
[7]Ba-NguV,Wing-KinM.Thegaussianmixtureprobabilityhypothesisdensityfilter[J].IEEE Trans.on Signal Processing, 2006,54(11):4091-4104.
[8]ZajicT,RavichandranRB,MahlerRP,etal.Jointtrackingandidentificationwithrobustnessagainstunmodeledtargets[C]∥Proc.of the International Society for Optics and Photonics, 2003:279-290.
[9]YangW,FuYW,LongJQ,etal.Jointdetection,tracking,andclassificationofmultipletargetsinclutterusingthePHDfilter[J].IEEE Trans.on Aerospace and Electronic Systems,2012,48(4):3594-3609.
[10]SmetsP,RisticB.KalmanfilterandjointtrackingandclassificationbasedonbelieffunctionsintheTBMframework[C]∥Proc.of the Information Fusion, 2007:16-27.
[11]LiuX,LeungH,ValinP,etal.MultisensorjointtrackingandidentificationusingparticlefilterandDempster-Shaferfusion[C]∥Proc.of the Information Fusion, 2012:902-909.
[12]SmetsP.DecisionmakingintheTBM:thenecessityofthepignistictransformation[J].International Journal of Approximate Reasoning, 2005,38(2): 133-147.
[13]SmetsP,KennesR.Thetransferablebeliefmodel[J].Artificial Intelligence, 1994,66(2):191-234.
[14]ClarkD,Ba-TuongV,Ba-NguV.Gaussianparticleimplementationsofprobabilityhypothesisdensityfilters[C]∥Proc.of the IEEE Aerospace Conference, 2007:1-11.
[15]LuoSH,XuH,XuY,etal.ImprovedMMPHDmethodfortrackingmaneuveringtargets[J].Acta Aeronautica et Astronautica Sinica, 2012,33(7):1296-1304.(罗少华,徐晖,徐洋, 等. 改进的MMPHD机动目标跟踪方法[J].航空学报, 2012,33(7):1296-1304.)
[16]SmetsP,KennesR.Thetransferablebeliefmodel[J].Artificial Intelligence,2008,66(94):191-234.
[17]HongyanZ,ChongzhaoH,YanL.ParticlelabelingPHDfilterformulti-targettrack-valuedestimates[C]∥Proc.of the Information Fusion, 2011:1-8.
[18]DanuDG,LangT,KirubarajanT.Assignment-basedparticlelabelingforPHDparticlefilter[C]∥Proc.of the SPIE Optical Engineering Applications, 2009.
[19]RisticB,Ba-NguV,ClarkD.Performanceevaluationofmulti-targettrackingusingtheOSPAmetric[C]∥Proc.of the Information Fusion, 2010:1-7.
[20]SchuhmacherD,Ba-TuongV,Ba-NguV.Aconsistentmetricforperformanceevaluationofmulti-objectfilters[J].IEEE Trans.on Signal Processing, 2008,56(8):3447-3457.
Multi-target joint tracking and classification based on model-class-matched PHD filter and TBM
ZHAN Kun, JIANG Hong, ZHAO Tian-qu, YU Yao-zhong
(Scool of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China)
To solve the multi-target joint tracking and classification under clutter and miss detection, the model-class-matched probability hypothesis density (PHD) filter is proposed and combined with the transferable belief model (TBM) framework of multiple sensors, and it is recursively implemented by multiple kinematic radars and particle filtering. In our algorithm, the priori information of aircraft is estimated to replace the attribute sensor. At the prediction stage, the particles of the PHD filter are matched by model and class; the particle weights are updated after the sensors receive the measurement information; then, the targets’ posterior state-model-class distribution is got by the corresponding weights of the particles; the targets’ state and class can be obtained simultaneously by these PHD filters; finally, by integrating TBM and the track particle labeling algorithm, the fusion result of multiple sensors is acquired. Simulations indicate that the performance of the proposed model-class-matched PHD filter is much better than that of the traditional PHD filter, and in the meantime the TBM framework of multiple sensors also improves the performance the proposed algorithm.
joint tracking and classification; probability hypothesis density (PHD); transferable belief model (TBM); particle filtering; multi-sensor data fusion
2015-10-13;
2016-06-24;网络优先出版日期:2016-07-18。
航空科学基金(2014ZC51042)资助课题
TP 721.1
A
10.3969/j.issn.1001-506X.2016.10.03
詹锟(1990-),男,硕士研究生,主要研究方向为目标跟踪、目标识别。
E-mail:zk_1028@buaa.edu.cn
蒋宏(1968-),女,副教授,博士,主要研究方向为目标跟踪、目标识别。
E-mail:jianghong2006@buaa.edu.cn
赵天衢(1990-),男,硕士研究生,主要研究方向为雷达配准。
E-mail:tianquzhao@163.com
于耀中(1991-),男,硕士研究生,主要研究方向为飞行器控制技术。
E-mail:yyz1991@126.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160718.1042.014.html
