基于GST-Hough变换的LFM信号识别方法

王红卫, 范翔宇, 陈　游, 杨远志

(1. 空军工程大学航空航天工程学院, 陕西 西安 710038;2. 西北工业大学电子信息学院, 陕西 西安 710072)



基于GST-Hough变换的LFM信号识别方法

王红卫1,2, 范翔宇1, 陈游1, 杨远志1

(1. 空军工程大学航空航天工程学院, 陕西 西安 710038;2. 西北工业大学电子信息学院, 陕西 西安 710072)

针对线性调频(linear frequency modulated, LFM)信号在低信噪比条件下的信号检测问题,提出将广义S变换(generalized S transform, GST)与Hough变换相结合(generalized S transform based on Hough transform,GSTH)信号检测方法。从理论层面推导出LFM信号在进行GST后对应的参数特性,论证Hough变换的可行性,推导出GSTH变换后LFM信号与噪声的概率密度分布函数,给出了基于奈曼-皮尔逊准则进行峰值检测时,检测门限的计算方法与确定流程。利用GST时频聚焦性提供良好的直线线性,有易于Hough变换的直线检测,提升变换后主峰峰值并降低副峰高度。通过与WHT (Wigner-Hough transform)、分数阶傅里叶变换与周期WHT算法的仿真对比,定量评估算法的适用性,并与经典算法对比,定性的描述出算法良好的时频聚焦性,凸显GSTH算法在强噪声背景下具有更好的检测精度与适用范围。

线性调频; 信号检测; 广义S变换; Hough变换; 概率密度分布函数; 奈曼-皮尔逊准则

0　引　言

线性调频(linear frequency modulation,LFM)信号是一种载频在脉冲宽度时间内线性变化的脉冲压缩信号,具有大时宽带宽积,广泛应用于通信、雷达、声呐和地震勘探等系统。在现代雷达中LFM信号具有提高雷达截获和目标跟踪能力,同时具备提高目标识别时距离维的强分辨能力。对其信号进行检测在雷达和电子对抗领域中具有重要的研究和应用价值[1-3]。

针对上述问题,学者们展开深入的研究并取得丰硕的成果。文献[4]采用压缩感知理论提高了在没有先验信息的条件下对LFM信号检测与参数估计的精确度,同时可以减少采样点数,降低信号处理系统的资源消耗,然而该方法要对于变换阶数进行搜索,增加了计算量;文献[5-6]基于压缩感知理论,通过构建波形匹配基用于LFM信号的检测,提高对于信号的检测效能;文献[7-8]通过设计匹配项的方式,将经典的WHT(Wigner-Hough transform)改进为周期WHT(periodic WHT,PWHT),利用信号的周期调制特性进行多维搜索,对周期性的能量进行积累,实现在强噪声背景下对弱LFM信号进行检测。上述方法取得良好的处理效果,然而其对于先验信息的依赖过强,在先验信息不足的情况下效能受限。在没有先验知识的情况下,构造匹配项时参数不易选取,当匹配基的数目过于庞大,利用优化算法检测信号时,每次都要在所有匹配基中遍历,算法计算量过大,降低系统的实时性并且在强窄带干扰情况下信号检测成功率不高。文献[9-10]借鉴LVD(Lv’s distribution)理论,将LFM信号进行LVD处理,得到具有高度能量聚集特性的变换结果,然而变换处理会受到噪声的干扰而严重恶化[11];文献[12-13]分别采用WHT理论与短时傅里叶变换用以实现对LFM信号的检测,可以直观地看出信号的特征,然而WHT处理会受到交叉项的影响,短时傅里叶变换的处理结果受到信噪比的严重制约,且采用小波变换理论得到的时频变换图的时频聚焦性有待进一步提升。

针对上述方法存在着对于先验信息需求与时频聚焦性的不足,本文借鉴WHT的思想,将广义S变换(generalized S transform, GST)与Hough变换相结合,提出了GSTH (GST based on Hough transform)变换方法用以实现对LFM信号的检测。由于广义S变换具有良好的时频聚焦性,且在进行GSTH之前不要求先验信息,更加贴近于现今的电子侦察实际作战应用需求。本文推导论证GSTH方法用于LFM信号识别的可行性,从理论层面推导出对LFM信号的检测方法,结合仿真验证,评估GSTH用于LFM信号检测的效能,从理论分析与仿真验证两个方面论证算法的有效性与适用性。

1　基本概念

1.1LFM信号与广义S变换

时域信号x(t)的短时傅里叶变换[14-15]为

(1)

式中，w(t)为窗函数;f为频率;τ为时移因子。将式(1)中的窗函数定义为归一化高斯窗,即

(2)

式中,σ=1/|f|为高斯窗的尺度因子。将式(2)代入式(1)中可得x(t)的S变换为

(3)

由式(2)可以看出,高斯窗的尺度因子与频率呈现反比关系,即对于处于低频的信号的具有较强的频率分辨能力,对于信号的高频部分具有较高的时间分辨率。由于在实际无源侦察中,为实现对于LFM信号的有效检测,且现今主战雷达的LFM信号处于较高的频段,即希望得到高频部分较好的频率分辨率。为了提升S变换的时频分辨能力,将尺度因子中加入调节系数p,则修正后的尺度因子可以表述为

(4)

式中，p>0。将式(3)进行改写,得到信号s(t)广义S变换为

(5)

广义S变换在S变换的基础上在核函数中添加了调节因子p,从而改善了S变换的时频分辨率,提高了时频聚焦性。因此,参数的确定直接决定着时频分辨能力的优劣,本文借鉴文献[16]提出的时频聚焦性度量准则,用以刻画在不同参数p对应的广义S变换的时频聚焦性。其定义如下:

(6)

式中,GST(t,f)为能量归一化的广义S变换的系数,即∑∑GST(t,f)=1,且p为大于1的常数。根据上述准则,可以得到计算最优p步骤如下[17-18]:

步骤 1对于任意p∈(0,1],利用式(5)对信号s(t)进行广义S变换;

步骤 2对广义S变换的系数进行归一化处理;

NGST(t,f)=GST(t,f)/∑∑|GST(t,f)

(7)

步骤 3选取p=2,根据式(6)计算广义S变换的时频聚焦性M(p);

步骤 4智能寻优,得到使M(p)为最小值的最优调节参数popt,即

(8)

将最优调节参数popt代入式(5),即可实现最优的广义S变换。

雷达系统采用的LFM信号的典型样式如下：

(9)

将典型的LFM信号代入式(5)中,可以得到LFM信号的广义S变换为

(10)

由于存在积分结果:

(11)

将式(10)中的被积函数分为两部分,将第1项与第2项看做第一部分,其积分结果为LFM信号广义S变换的幅值项,第二部分为式(10)中最后的自然底数一项,积分结果为冲击函数,由于冲击函数本身并不存在幅度。因而第一项对LFM信号的积分结果没有影响,即LFM信号的广义S变换的结果为

(12)

即为在t-f二维域的解析式为f=f0+0.5mt的直线,进而可以利用Hough变换进行直线检测。

1.2Hough变换原理

Hough变换是现今较为成熟的图像边缘检测方法,用以识别和检测出图像中的解析曲线。Hough变换利用图像空间和Hough参数空间的线-点对偶性,通过在参数空间进行简单的累加统计,然后在Hough参数空间寻找累加得到的峰值方法实现直线检测。Hough变换的实质是将图像空间内具有一定关系的像元进行聚类,寻找能把这些像元用某一解析形式联系起来的参数空间累积对应点[19]。

直线y=kx+b用极坐标可以表述为

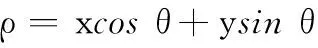
(13)

式中,θ表示直线的法线方向;ρ表示原点到直线的距离。

首先，按照一定的量化间隔将可能的θ和ρ离散化为可能的若干区间。θ的取值范围一般为[-90°,90°),ρ的取值范围则由图像的矩形顶点至图像中心的距离确定;将整个θ-ρ平面细化为一个二维网格,x-y平面的上的直线即可转化为θ-ρ平面上的一个点。对每个可能的离散化参数对(θi,ρi)设置一个计数器;然后，将图像中的每个特征点(x0,y0),遍历所有的离散θ值,根据式(13)计算每个θi值下对应的ρ值及相应的离散区间ρj;并对计数器的值加1。当所有的特征点遍历后,即可通过峰值搜索实现对于原始图像的直线检测。

2　GSTH原理与处理流程

在时频二维域进行直线检测的原理实际为沿着t-ω平面上的直线积分,在标准参数化方程下,根据式(13),可得在时频域Hough变换的表达式为

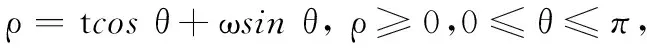
(14)

由Hough变换的原理可知,如果时频平面上存在直线,则在ρ-θ域内将出现峰值。在时频平面上,若用ω的截距ω0和k斜率描述直线,当沿着ω=ω0+kt积分时,可以将被积函数进行积分变换

(15)

综合GST和Hough变换,得到信号的LFM广义S变换后的Hough(GSTH)变换为

(16)

从式(16)可以看出,由于LFM信号的广义S变换为在t-ω平面上为能量集中地一条直线,采用Hough变换后在ρ-θ域内为一个峰值,而当信号自身的参数偏离ω0和k时,对应的积分值会快速下降,而噪声的GSTH变换没有规律可言,且信号的干扰项虽然在t-ω平面会影响LFM信号的甄别,然而对干扰项进行GSTH变换后其参数不在ω0和k附近。因此,理论上采用GSTH变换对LFM信号进行检测时可以良好地抑制干扰项和噪声的影响。图1为GSTH对LFM信号的处理流程。

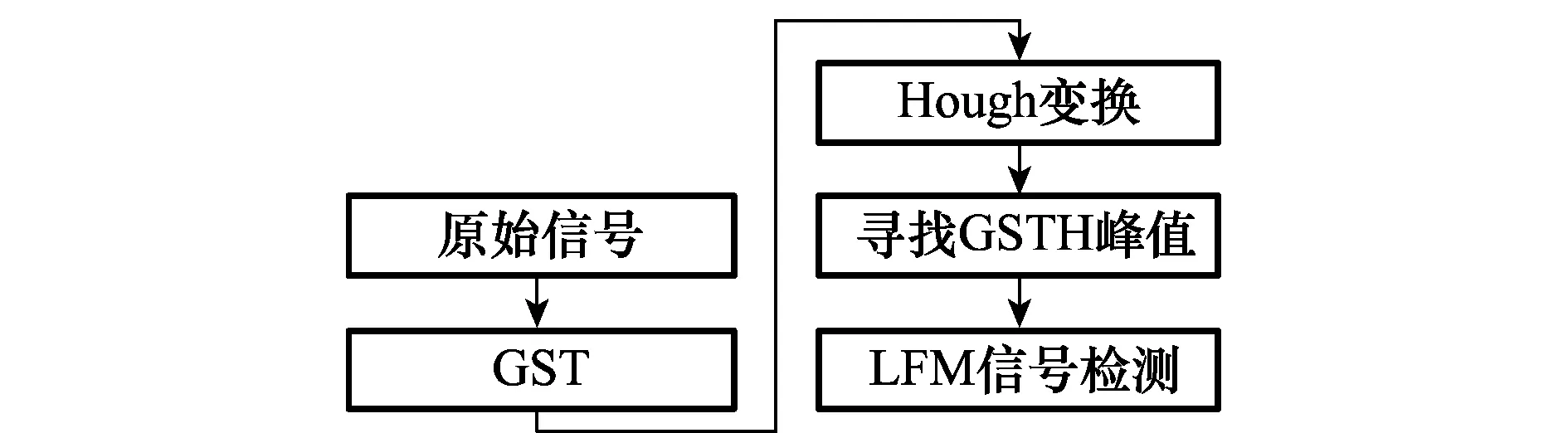
图1　GSTH对LFM信号的处理流程Fig.1　Flow of GSTH’s processing LFM signal

首先利用式(5)对LFM信号进行广义S变换,再利用Hough变化将参数对(θ,ρ)遍历最终对所得到的结果进行峰值搜索,实现对LFM信号进行检测。GSTH方法的核心是由于LFM信号在进行广义S变换后,在时频域内表现为一条直线,进而可以采用Hough变换将直线转化为ρ-θ域内的峰值点,再对Hough变换的结果进行峰值检测,即可实现对LFM信号的检测。

3　LFM信号的检测算法

从电子对抗侦察方的角度而言,在进行侦察之前会得到部分关于敌方雷达的先验信息,然而在实际作战中对战双方的信号参数会有一定幅度的改变,因而侦察得到的先验信息有可能不足以支撑信号的匹配检测。本文采用统计信号检测的方式实现对多个LFM信号进行检测,由于多个LFM在进行GSTH后会在ρ-θ维度内形成对个峰值,因为本文将对多个LFM信号检测转化为多个二元假设检验问题,即将信号的峰值与设定的门限进行比对,判定侦收结果为噪声或者信号加噪声。设LFM信号为s(t),噪声为n(t),则上述的二元检测可以表示为

(17)

为适应这种不能预知先验概率且无法判定错误判断的代价因子的情况,本文利用奈曼-皮尔逊准则设计信号检测器,采用奈曼-皮尔逊准则能够保证检测器中能够有效的利用信号数据,同时也能够避免过多的虚假数据进入检测系统影响检测效能。即在错误判决概率P(H1|H0)=α的约束条件下,使得正确判定概率P(H1|H1)最大。在进行Hough变换后,信号在ρ-θ维度内表现为峰值,而噪声在进行Hough变换后在ρ-θ域内其幅值并不会明显提升,因此可以设定其检测门限α用以检测信号与噪声,并设检验统计量l(ρ,ω)为

(18)

得到信号的检测概率PD与虚警概率PF,可以表示为

(19)

(20)

奈曼-皮尔逊准通过设定检测概率PF为定值PFc,利用式(19)对H0条件下检验统计量l(ρ,ω)的概率密度函数p(l|H0)进行变下限的广义积分,使其积分值为PFc,可以得到此时的积分下限,即需要确定的门限α。再采用式(20)进行积分,便可得到恒虚警条件下最佳的检测概率PD。即采用恒虚警检测要根据实际作战需求与应用环境设定系统的虚警率PFc,利用上式与信号参数的统计特性确定系统的检测门限。通过过门限检测方式实现对于信号与噪声的甄别。

侦察截获接收机处于无源侦收状态,噪声中幅值最强且影响程度最大的干扰信号为系统内部的热噪声,其统计特性为高斯白噪声[21]。即n(t)～N(0,1),其中N(0,1)表示均值为0,方差为1的标准高斯分布。利用式(5)对高斯白噪声进行广义S变换,可得

(21)

将式(21)进行离散化,令t=mT,f=n/NT,τ=λT。其中，T为采样时间间隔,N为总的采样点数,则离散广义S变换可以表示为

(22)

式中,λ,m,n=0,1,…,N-1。再进行Hough变换可得

(23)

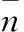
(24)

通过上述的推导,可以得到检测环境噪声的概率密度分布函数为高斯白噪声。由于无法确定LFM信号是否存在,将对LFM信号转化为二元数字通信中高斯噪声环境下信号检测问题,借鉴文献[20](P87-88)的结论,得到

(25)

(26)

得到了检验统计量l在H0条件下的概率密度函数,可以利用式(19)对p(l|H0)进行广义积分,令积分结果为系统预先设定好的而接受的虚警概率PFc,进而得到检测门限α。同时得到了检验统计量l在H1条件下的概率密度分布函数,进而可以利用式(20)求出信号的检测概率PD。上述的处理流程如图2所示。

图2　基于GSTH的LFM信号检测流程Fig.2　Detecting flow of LFM signal based on GSTH

图2即为图1中信号检测的部分,通过上述流程,即可在信号GSTH处理后进行LFM信号的检测。

4　仿真验证

本节首先利用GSTH变换,并结合第3节的检测流程,对高斯白噪声背景下LFM信号检测能力进行仿真分析,并与传统与改进的算法进行横向对比,定量研究GSTH的性能,分析处理结果。

为验证GSTH变换对单LFM信号的检测能力,本文将仿真条件设定为单LFM与高斯白噪声的混合信号。LFM信号变化范围为[0 MHz,30 MHz],信号采样频率fs=100 MHz,系统采样点数N=1 024,总的观测时间Tt=N/fs=10.24 μs,频率变化率Δf1=2.93 MHz/μs,初始频率f0=0,初始相位φ在[0,2π]内随机取值。设虚警概率为0.01。为对比清晰,首先得到无噪声条件下LFM信号与信噪比为-15 dB条件下GST与GSTH变换图,仿真结果如图3所示。

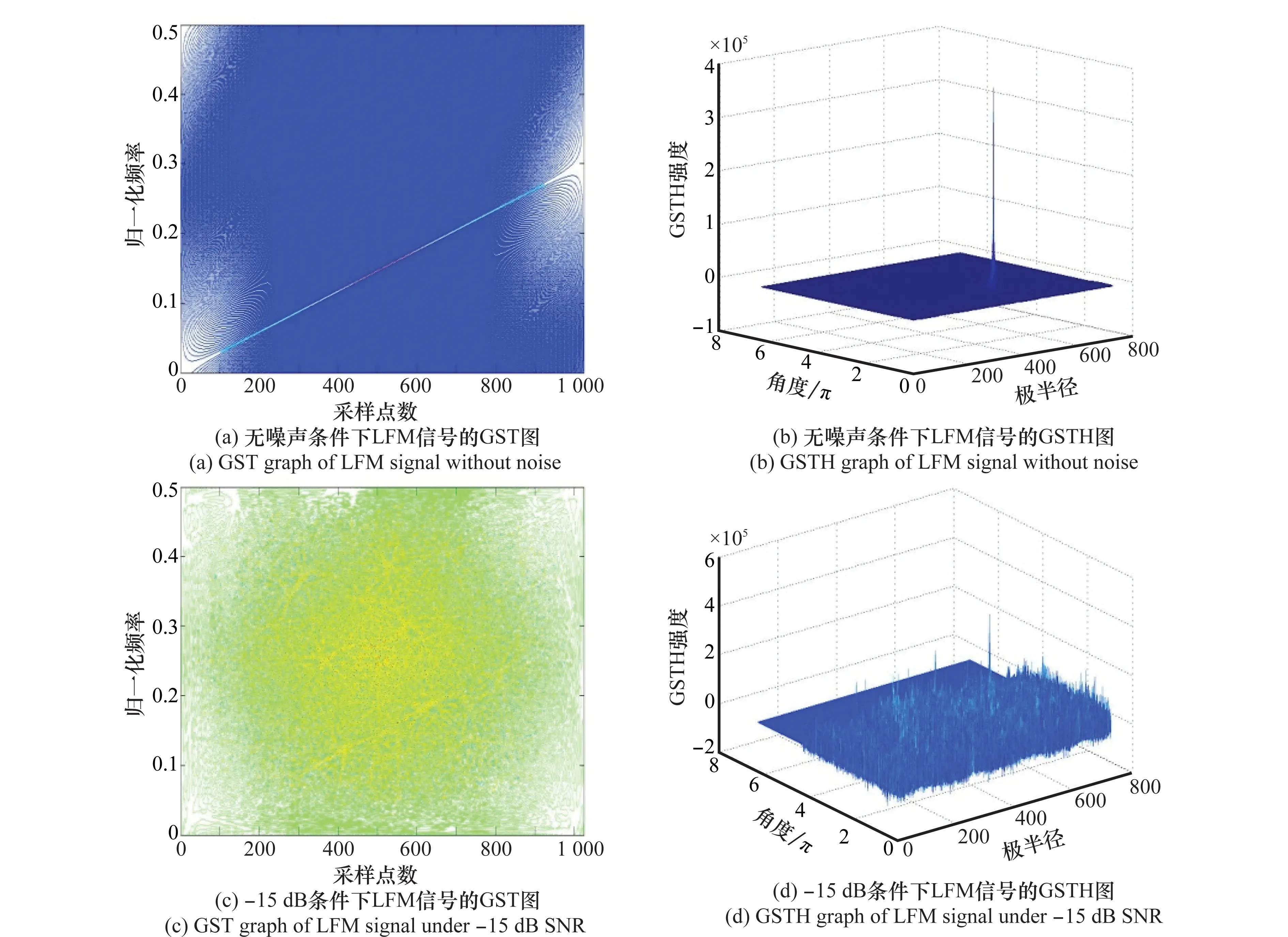
图3　LFM信号的GST与GSTH图Fig.3　GST and GSTH graphs of LFM signal

从图3(a)可以看出,对LFM信号进行广义S变换后,其时频特性为一条明显的直线,且线形较细,说明广义S变换得到的结果具有良好的时频聚焦,更有利于进行LFM信号的检测。同时从图3(b)可以看出,对单LFM信号采用Hough变化后,在ρ-ω域内出现明显的峰值,即可以通过峰值检测实现对于LFM信号的识别。从图3(c)、图3(d)可以定性看出,对处于背景噪声为-15 dB的条件LFM信号进行GST与GSTH变换后得到的结果较为可观,图3(c)在与图3(a)相同的位置处出现了直线,图3(d)也在与图3(b)相同的点上出现了峰值。

为研究本文算法对于低信噪比情况下对LFM信号检测的能力,将仿真条件设定为-20 dB的信噪比,将本文算法与经典的WHT算法进行对比,得到上述LFM信号的WHT图与GSTH图,具体如图4所示。

图4　-20 dB条件下LFM信号的WHT与GSTH图Fig.4　WHT and GSTH graphs of LFM signal under -20 dB SNR

通过图4(a)和图4(b)对比可以看出,经过GSTH变换得到的仿真结果较WHT的结果有明显提升。因为GSTH变换处理得到的结果时频聚焦性强于WHT中魏格纳-威利处理结果,采用改进的核函数提升了信号的能量聚焦性,从而使得到的时频分布图的直线性更强,再进行Hough变换后,峰值信号更容易被识别与检测。

现今的雷达信号通过调控发射功率,降低峰值功率,实现从能量维度降低其被截获的概率,这就要求侦察截获接收机具有较强的在低信噪比条件下提取弱信号的能力,才能实现对LFM信号的检测。

为体现算法的抗噪声性能,本文将信噪比设定为-25～0 dB,进行500次蒙特卡罗实验,并借鉴文献[21-23]已有的研究成果,得到信噪比与检测概率PD之间的关系如图5所示。

图5　不同信噪比条件下的检测概率Fig.5　Detection probability under various signal-to-noise ratio

从图5可以定量而直观的看出,经典的WHT变换与分数阶傅里叶变换(fractional Fourier transform,FrFT)在信噪比低于-13 dB后检测性能明显恶化。当检测概率均取0.9的条件下,GSTH相较于WHT与FrFT变换可以降低约5 dB的检测需求,更有益于在强噪声中检测出弱LFM信号,实现对于低截获雷达信号的有效检测。由于广义S变换的核函数相较于经典的WHT与FrFT具有良好的时频聚焦性,同时结合第1节的理论推导可得,LFM信号的GSTH变换为一条直线,得到的结果相较于现有的经典变换具有更好的直线线性,有益于提升Hough变换的主峰峰值,同时降低副峰的影响,进而获得相较于经典的变换有了较大幅度的改善。随着信噪比的不断下降,GSTH相较于传统的WHT与FrFT变换的相对检测概率差越来越大,因此GSTH变换具有更好的应用前景。

对比GSTH变换与周期WHT(periodic WHT, PWHT)可得,虽然在低信噪比条件下GSTH变换的检测性能略逊色于PWHT,但PWHT变换处理要求有一定量的先验信息作为情报支撑,用以设计变换时的匹配项,这种需求能否适应日益复杂的电磁环境还有待进一步商榷,可本文提出的算法具有更强的适用范围,有助于实现在强噪声环境中检测LFM信号。

同时,为提升对于LFM信号的检测能力,并降低噪声的干扰,本文在对信号进行峰值检测时基于奈曼-皮尔逊准则设计了接收机,从而降低了虚假信息干扰信号检测的可能。同时从公式层面推导出了LFM信号与高斯白噪声经过GSTH变换后的概率密度分布函数,用以支持恒虚警检测时需要的分布函数与特性参数,进一步提升对于在低信噪比条件下,对LFM信号的检测性能。

5　结　论

(1) 本文借鉴WHT的思想,将主流的广义S变换与Hough变换相融合,提出了GSTH用以检测LFM信号,首先推导出LFM广义S变换后的解析表达与参数特性,论证了将其进行Hough变换的可行性,为本算法提供理论支撑;

(2) 推导得到了GSTH变换后LFM信号与高斯白噪声的概率密度分布函数,给出了基于奈曼-皮尔逊准则设定门限的计算方法与确定流程,有助于实现GSTH变换后对LFM信号的恒虚警检测;

(3) 由单个信号入手,仿真验证了该算法适用于LFM信号的识别与检测,同时将本文算法与现有的算法进行横向对比,量化方法分离能力,该算法具备良好的处理结果与拓展性能;多信号的检测可以视为多个单信号的检测,本算法依旧可以应用于多信号;

(4) 本文算法可以实现在低信噪比条件下对于LFM信号的识别,并具有随着信噪比的提升,检测性能明显提升的特点,从而能够有效地抑制噪声的影响,可以不用先验信息作为支撑,本算法具备良好的使用前景与推广性能。

[1] Bi G A, Li X M, Samson S C M. LFM signal detection using LPP-Hough transform[J].SignalProcessing, 2011, 91(6): 1432-1443.

[2] Ma N, Wang J X, Dong N F. Parameter estimation of sub-sampling LFM signal based on orthogonal matching pursuit[J].JournalofElectronics&InformationTechnology, 2013, 35(8): 1888-1893. (马宁, 王建新, 董宁斐.基于正交匹配追踪的欠采样LFM信号参数估计[J].电子与信息学报, 2013, 35(8): 1888-1893.)

[3] Gong S X, Wei X Z, Li X, et al. Mathematic principle of active jamming against wideband LFM radar[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 50-60.

[4] Yan H, Dong C X, Zhao G Q. Parameter estimation of LFM signal based on compressed sensing[J].ChineseJournalofRadioScience, 2015, 30(3): 449-456. (闫浩, 董春曦, 赵国庆. 基于压缩感知的线性调频信号参数估计[J].电波科学学报, 2015, 30(3): 449-456.)

[5] Shi G M, Lin J, Chen X Y, et al. UWB echo signal detection with ultra-low rate sampling based on compressed sensing[J].IEEETrans.onCircuitsandSystemsⅡ:ExpressBriefs, 2008, 55(4): 379-383.

[6] Liu B, Fu P, Xu C, et al. Parameter estimation of LFM signal with compressive measurements[J].JournalofConvergenceInformationTechnology, 2011, 6(3): 303-310.

[7] Geroleo F G, Pearce M B. Detection and estimation of multi-pulse LFMCW radar signals[C]∥Proc.oftheIEEEInternationalRadarConference, 2010: 1009-1013.

[8] Geroleo F G, Pearce M B. Detection and estimation of LFMCW radar signals[J].IEEETrans.onAerospaceandElectronicSystems, 2012, 48(1): 405-417.

[9] Jin Y, Duan P T, Ji H B. Parameter estimation of LFM signals based on LVD in complicated noise environments[J].JournalofElectronics&InformationTechnology, 2014, 36(5): 1106-1112. (金艳, 段鹏婷, 姬红兵.复杂噪声环境下基于LVD的LFM信号参数估计[J].电子与信息学报, 2014, 36(5): 1106-1112.)

[10] Lv X L, Bi G A, Wan C R, et al. Lv’s distribution: principle, implementation, properties, and performance[J].IEEETrans.onSignalProcessing, 2011, 59(8): 3576-3591.

[11] Li L, Qiu T, Song D. Parameter estimation based on fractional power spectrum under alpha-stable distribution noise environment in wideband bistatic MIMO radar system[J].AEU-InternationalJournalofElectronicsandCommunications, 2013, 67: 947-954.

[12] Liu F, Xu H F, Sun D P, et al. Feature extraction of symmetrical triangular LFMCW signal using Wigner-Hough transform[J].JournalofBeijingInstituteofTechnology,2009,18(4):478-483.

[13] Pei S C, Huang S G. STFT with adaptive window width based on the chirp rate[J].IEEETrans.onSignalProcessing, 2012, 60(8): 4065-4080.

[14] Djurovi I, Sejdi E, Jiang J. Frequency-based window width optimization for S-transform[J].AEU-InternationalJournalofElectronicsandCommunications, 2008, 62(4): 245-250.

[15] Sejdi E, Djurovi I, Jiang J. A window width optimization S-transform[J].EURASIPJournalonAdvancesinSignalProcessing, 2008, 2008: 1-13.

[16] Chi H S, Wang H X, Zhang M, et al. Time-frequency concentration enhancement for time-phase modulation based on generalized S transform[J].JournalofBeijingUniversityofPostsandTelecommunications, 2012, 35(1): 125-128. (迟华山, 王红星, 张敏, 等. 基于广义S变换的时相调制时频聚集性能优化[J].北京邮电大学学报, 2012, 35(1): 125-128.)

[17] Stankovi I. A measure of some time-frequency distributions concentration[J].SignalProcessing, 2001, 81(3): 621-631.

[18] Zhang Y Q, Zhang P L, Wu D H, et al. Bearing fault diagnosis based on optimal generalized S transform and pulse coupled neural network[J].JournalofVibrationandShock, 2015, 34(9): 26-31. (张云强, 张培林, 吴定海, 等.基于最优广义S变换和脉冲耦合神经网络的轴承故障诊断[J].振动与冲击, 2015, 34(9): 26-31.)

[19] Yu X L, Chen Q, Gu G H. Multi-sensor image registration method based on phase congruency and Hough transform[J].HighPowerLaserandParticleBeams, 2013, 25(9): 2223-2228.(于雪莲,陈钱,顾国华.基于相位一致性和Hough变换的多源图像匹配方法[J].强激光与粒子束,2013,25(9):2223-2228.)

[20] Zhao S J, Zhao J X.Thetheoryofsignaldetectionandestimation[M]. Beijing: Tsinghua University Press.2005:87-88. (赵树杰,赵建勋. 信号检测与估计理论[M]. 北京:清华大学出版社,2005:87-88.)

[21] Zhang L M, Zhong Z G, Wang Z Z, et al. Detection and separation of overlapped quasi-LFMCW signals based on periodic WHT recurrent filter[J].ActaAeronauticaetAstronauticaSinica, 2013,34(11):2580-2589.(张立民,钟兆根,王泽众,等.基于周期WHT循环滤波的交叠类似LFMCW信号检测与分离[J].航空学报,2013,34(11):2580-2589.)

[22] Liu F, Sun D P, Huang Y, et al. Multi-component LFM signal feature extraction based on improved Wigner-Hough transform[J].TransactionsofBeijingInstituteofTechnology,2008,28(10):914-918.(刘峰,孙大鹏,黄宇,等.基于改进Wigner-Hough变换的多分量LFM信号特征提取[J].北京理工大学学报学报,2008,28(10):914-918.)

[23] Liu F, Xu H F, Tao R, et al. Research on resolution among multi-component LFM signals in the fractional Fourier domain[J].ScienceChina：InformationSciences,2012,55(6):1301-1312.

Recognition method of LFM signals based GSTH transform

WANG Hong-wei1,2, FAN Xiang-yu1, CHEN You1, YANG Yuan-zhi1

(1. College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’an 710038, China;2.CollegeofElectronicandInformation,NorthwesternPolytechnicalUniversity,Xi’an710072,China)

Aiming at the linear frequency modulated (LFM) signal detection under the low signal-to-noise ratio, generalized S transform based on Hough transform (GSTH) which combines generalized S transform and Hough transform is put forward. Parameter characteristics of LFM signals after GST were derived in theory and the possibility of Hough transform was demonstrated, the probability density distribution functions of LFM signal and noise after GSTH are derived, the calculation method and flowchart of the detection threshold are given when conducting peak detection based on the Neyman-Pearson rule. The time-frequency focusing property of GST is used to provide nice linear characteristics which benefit line detection of Hough transform and promoted main peak while reducing the height of the second peak. The feasibility of the algorithm is tested according to the GSTH’s simulation comparisons with Wigner-Hough transform (WHT), fractional Fourier transform and periodic WHT. Besides, compared with the classical algorithm, the nice time-frequency focusing property is qualitatively described, the better detection precision and application scope of GSTH under strong noise are highlighted.

linear frequency modulated (LFM); signal detection; generalized S transform (GST); Hough transform; probability density distribution function; Neyman-Pearson criterion

2016-01-25；

2016-06-15；网络优先出版日期：2016-07-05。

航空科学基金(20145596025，20152096019)资助课题

TN 97

A

10.3969/j.issn.1001-506X.2016.10.02

王红卫(1974-),男,副教授,硕士研究生导师,博士,主要研究方向为电子对抗理论与技术。

E-mail:hww0818@163.com

范翔宇(1991-),男,硕士研究生,主要研究方向为电子对抗理论与技术。

E-mail:panda0077@163.com

陈游(1983-),男,讲师,博士,主要研究方向为电子对抗理论与技术。

E-mail:chenyousky@163.com

杨远志(1991-),男,硕士研究生,主要研究方向为电子对抗理论与技术。

E-mail:yyzyangyuanzhi@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160705.1944.012.html