α稳定分布噪声下一种稳健加权滤波的统一框架
2016-10-18胡碧昕姬红兵
金 艳, 胡碧昕, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
α稳定分布噪声下一种稳健加权滤波的统一框架
金艳, 胡碧昕, 姬红兵
(西安电子科技大学电子工程学院, 陕西 西安 710071)
针对传统滤波方法在α稳定分布噪声环境下性能退化的问题,从加权Myriad滤波以及加权Merid滤波方法出发,以M估计理论为基础,推导得到稳健加权(robust weighted,RW)滤波方法的统一算法结构,并据此提出了基于RW滤波的新算法,即基于稳健加权滤波的统一框架,从而将加权Myriad、加权Merid以及基于广义柯西分布的加权滤波器统一起来。此外,针对线性调频(linear frequency modulation, LFM)信号采用基于RW的LVD(RW-LVD)方法估计其参数,并根据估计性能对RW方法的抑噪效果进行分析。仿真结果表明,与基于加权Myriad滤波、加权Merid滤波以及基于广义柯西分布的加权滤波等多种方法相比,在强脉冲噪声下RW滤波方法能有效抑制脉冲噪声,并具有良好的稳健性。
α稳定分布噪声; 参数估计; 代价函数; 稳健加权滤波
0 引 言
在雷达、声呐、生物工程、地震探测等领域中,实际噪声具有明显的非高斯脉冲特性,较厚的概率密度函数拖尾,与传统高斯模型相比,α稳定分布可以更好地描述[1-4]。α稳定分布是唯一满足广义中心极限定理的分布,因而在信号处理领域得到快速发展。针对该类噪声下基于传统高斯模型的信号处理方法性能下降的问题,已有学者提出了基于加权Myriad滤波[5-8]以及加权Merid滤波[9-11]等多种降噪方法。这些方法在一定程度上抑制了α稳定分布噪声,但在强脉冲噪声环境下性能均会下降。
对此,本文提出了可有效抑噪的稳健加权(robust weighted,RW)滤波新方法,该方法基于M估计原理,构造了适用于较强脉冲噪声的代价函数。由于α稳定分布噪声不存在统一的封闭概率密度函数表达式,加权Myriad、加权Merid滤波器均基于α稳定分布中唯一存在封闭概率密度函数表达式的柯西分布,并采用最大似然估计方法对噪声进行抑制,然而在强脉冲噪声下其抑噪性能退化。本文构造的代价函数无需获得样本的概率密度函数,从而解决了传统加权滤波器采用最大似然估计,与α稳定分布噪声不存在封闭的概率密度函数表达式的矛盾。此外,基于该代价函数的RW滤波方法,建立了α稳定分布噪声下稳健加权滤波的统一框架,从而将加权Myriad、加权Merid以及基于广义柯西分布的加权(weighted maximum-likelihood generalized Cauchy,WMGC)滤波器[12]有机统一起来,构建起RW滤波的统一理论基础,并从滤波器输出及代价函数两个方面说明以上3种滤波器服从于本文提出的RW滤波框架。
线性调频(linear frequency modulation, LFM)信号是研究最早且应用最广的一种脉冲压缩信号,在通信、雷达和地震勘探等方面均有广泛应用[13-14]。Lv’s分布(Lv’s distribution,LVD)算法结合相位尺度变换[15],无需进行二维搜索,具有较高的时频分辨率,但在脉冲性较强的α稳定分布噪声下该方法性能退化严重。因此,本文首先对α稳定分布噪声下的LFM信号进行RW滤波,随后对滤波后信号进行LVD时频分析,并利用LFM信号参数估计的结果表明该方法的噪声抑制性能。此外,需要说明的是,该方法不仅适用于线性调频信号,在α稳定分布噪声环境下均可适用,采用线性调频信号仅是作为验证噪声抑制性能的一个角度,用以说明方法在α稳定分布噪声下的有效性。
1 最大似然估计与M估计原理
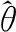
(1)
式中,f(xi;θ)为样本的概率密度函数,对似然函数求导,令
(2)
(3)
式(3)也可描述为
(4)
式中,ρ(·)是代价函数;φ(·)为ρ(·)关于θ的导数[16]。最大似然估计中求取似然函数最大值的问题,可转化为求取似然函数倒数最小值的问题。因此,最大似然估计与M估计理论均可等效为最小值求取问题。当代价函数为ρ(X)=X2时,式(3)所描述的M估计即等价于高斯假设下的最大似然估计。此外,通过构造合适的代价函数,M估计可应用于脉冲噪声环境并具有良好的稳健性。
2 RW滤波原理及RW原理统一框架
2.1RW滤波方法
广义柯西(generalized Cauchy,GC)分布的概率密度函数为
(5)
式中
(6)
式中,k为尺度参数;p是拖尾参数,在区间(0,2]取值;Γ(·)是Gamma函数。由于广义柯西分布的拖尾参数仅可在较小范围内取值,导致基于该分布的滤波器的适用范围、抑噪效果等性能受限。对此,本文引入辅助参数q,以扩大拖尾参数的选取范围,进而扩大滤波器的适用范围。在此基础上构造基于RW滤波的代价函数为
(7)
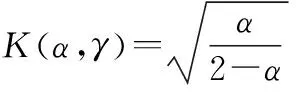
根据式(3)和式(5),RW滤波的目标函数可表示为
(8)
此时,若给定一组观测样本{x1,x2,…,xN}及非负滤波权值{h1,h2,…,hN},由M估计理论可得RW滤波的输出为
(9)
(10)
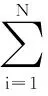
(11)
由式(10)和式(11)可得
(12)
式中
令观测样本X=[x1,x2,…,xN],对应的初始权值向量H=[h1,h2,…,hN],尺度参数为k,可得该滤波器的输出和估计误差分别为θ(h,X),e=θ-d,其中d是滤波器期望输出。根据平均绝对误差最小的准则求得最佳权系数,设误差函数J(h,k)为
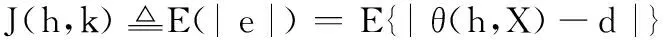
(13)
由式(13)可知,J(h,k)可能存在多重极小值点,而最优权值就是其中的一个。令
(14)
即可得滤波器权值的迭代关系式为
(15)
式中,μ是迭代步长;函数P[·]为矩形函数;变量hj是第j个权值,hj(n),hj(n+1)分别为第n次和第n+1次迭代值[11]。
当h取实数时,RW滤波的输出和权值迭代表达式分别为
(16)
(17)
式中,zi=sgn(hi)xi。
2.2RW滤波的统一框架
本文提出的RW滤波方法适用范围广泛,并且建立了一种RW滤波统一框架,该框架将加权Myriad、加权Merid以及WMGC滤波器统一起来,构建了RW滤波的统一理论基础。本节从滤波器输出和代价函数的构造两个角度,说明以上3种滤波器均可用本文提出的基于RW滤波器的统一框架描述。
加权Myriad滤波器是从样本序列服从柯西分布的Myriad平滑器中推导得来的,若给定一组观测样本及非负滤波权值{h1,h2,…,hN},Myriad滤波器输出可表示为
(18)
与式(9)对比可知,RW滤波器中参数满足p=-q=2时即为加权Myriad滤波。
加权Merid滤波器的样本序列服从p=1时的GC分布,其滤波器输出可表示为
(19)
与式(9)对比可知,RW滤波器中参数满足p=-q=1时即为加权Merid滤波。
假设N个独立样本{x1,x2,…,xN}满足位置参数为θ、尺度参数为k的GC分布,由式(5)及式(6)可知,WMGC滤波器输出可表示为
(20)
与式(9)对比可知,RW滤波器中参数满足p=-q时即为WMGC滤波。可见以上3种滤波器均可用本文提出的基于RW滤波器的统一框架描述。
此外,通过对最大似然函数与M估计分析比较,可知基于最大似然估计原理的3种滤波器,均可从M估计角度进行定义:当代价函数为ρ(xi)=lg{k2+hi|xi-θ|2}时,可定义加权Myriad滤波器;选取为ρ(xi)=lg{k+hi|xi-θ|}时,可定义加权Merid滤波器;选取为ρ(xi)=lg{kp+hi|xi-θ|p}时,可定义WMGC滤波器。将以上3种滤波器的代价函数分别与式(7)对比也可看出,三者均服从本文构造的RW统一框架。
综上所述,加权Myriad、加权Merid以及WMGC滤波器均可用本文构造的RW统一框架描述。由于α稳定分布噪声不具备封闭的概率密度函数表达式,以上3种稳健滤波器均基于α稳定分布下的特例,并采用最大似然估计获得滤波器输出,导致该类滤波器在脉冲噪声下滤波性能有限。本文构造的RW统一框架则从M估计角度出发,无需依靠样本的概率密度函数,可在α稳定分布环境下具有更好的噪声抑制性能。此外,其有机地将多种传统加权滤波器统一起来,构建了RW滤波的统一理论基础。
3 LVD原理
RW滤波从M估计角度构造稳健性较强的代价函数,实现了对较强脉冲噪声的抑制。为验证各滤波器的抑噪效果,本文采用LVD对滤波后的信号进行时频分析。LVD算法能够使LFM信号在初始频率-调频斜率(centroidfrequency-chirprate,CFCR)域表现为一峰值,该峰值对应的横纵坐标即为LFM信号的初始频率和调频斜率值。首先,对信号的对称参数瞬时自相关函数(parametricsymmetricinstantaneousautocorrelationfunction,PSIAF)做尺度变换,消除时间变量之间的耦合关系。PSIAF定义如下:
(21)
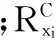
(22)
式中,h是尺度因子[15]。对尺度变换后的PSIAF分别关于τ和tn进行二维傅里叶变换,即得LVD的定义式:
(23)
LVD具有较高的能量聚集性,可较为准确地对LFM信号进行参数估计,但其在脉冲性较强的α稳定分布噪声下性能严重退化。因此,本文首先对信号进行RW滤波,再采用LVD对滤波后LFM信号进行参数估计,并用其结果表示各滤波方法的抑噪效果。
4 仿真实验及分析
LFM信号的数学模型定义如下:
(24)
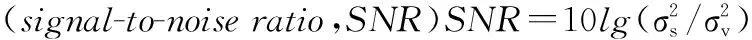
(25)
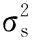
仿真中LFM信号参数为:采样频率fs=256Hz,初始频率f0=50Hz,调频斜率k=25Hz/s,采样点数N=256。
4.1方法性能比较
本文提出的RW滤波方法分别与基于加权Myriad滤波器[5-8]的LVD(myriadLVD,MYRLVD)、基于加权Merid滤波器[9-11]的LVD(meridLVD,MELVD)以及基于WMGC滤波器[12]的LVD(WMGCLVD)方法进行对比。RW滤波中参数p与GC分布的拖尾参数一致,均在区间(0,2]取值。由于GC分布加权滤波器拖尾参数选取范围较窄,导致其适用范围、抑噪效果等性能受限。本文针对脉冲性较强的α稳定分布,构造了可扩大拖尾参数选取范围的参数q。大量仿真实验证明,在p∈(0,2],p+q∈(0,80]区间内,RW滤波均可抑制脉冲噪声,而WMGC滤波器则仅适用于p∈(0,2],p+q=0,可见,通过引入辅助参数q,RW滤波有效地扩大了拖尾参数的选取范围,进而获得更为广泛的适用范围。特别地,当参数选取为p∈(0,2],p+q∈(0,5]时,RW滤波可在α稳定分布噪声下取得良好的抑噪效果。为方便说明且不失一般性,本文设置RW滤波器参数p=1.4,q=2.0,窗长N=5,初始权向量h=[0,0,5,0,0],步长因子μ=0.05。
图1(a)为LFM信号的LVD等高线图,可见,LFM信号在CFCR域清晰明确,可直接获得LFM信号初始频率和调频斜率。图1(b)~图1(f)是α=0.8,GSNR=3dB的α稳定分布噪声下,采用不同方法所得的LVD等高线图。图1(b)为脉冲噪声环境下采用LVD所得的等高线图,由图可知,受脉冲噪声影响LVD分析方法性能严重退化。由图1(c)、图1(d) 以及图1(e)可知,Myriad、Merid以及WMGC3种滤波器能够较为有效地抑制脉冲噪声,但仍难以对噪声下的LFM信号进行准确分析。图1(f)为RW滤波下的LVD(RW-LVD)等高线图,可以看出,其与LFM信号的LVD等高线图接近,RW滤波具有良好的脉冲噪声抑制效果。
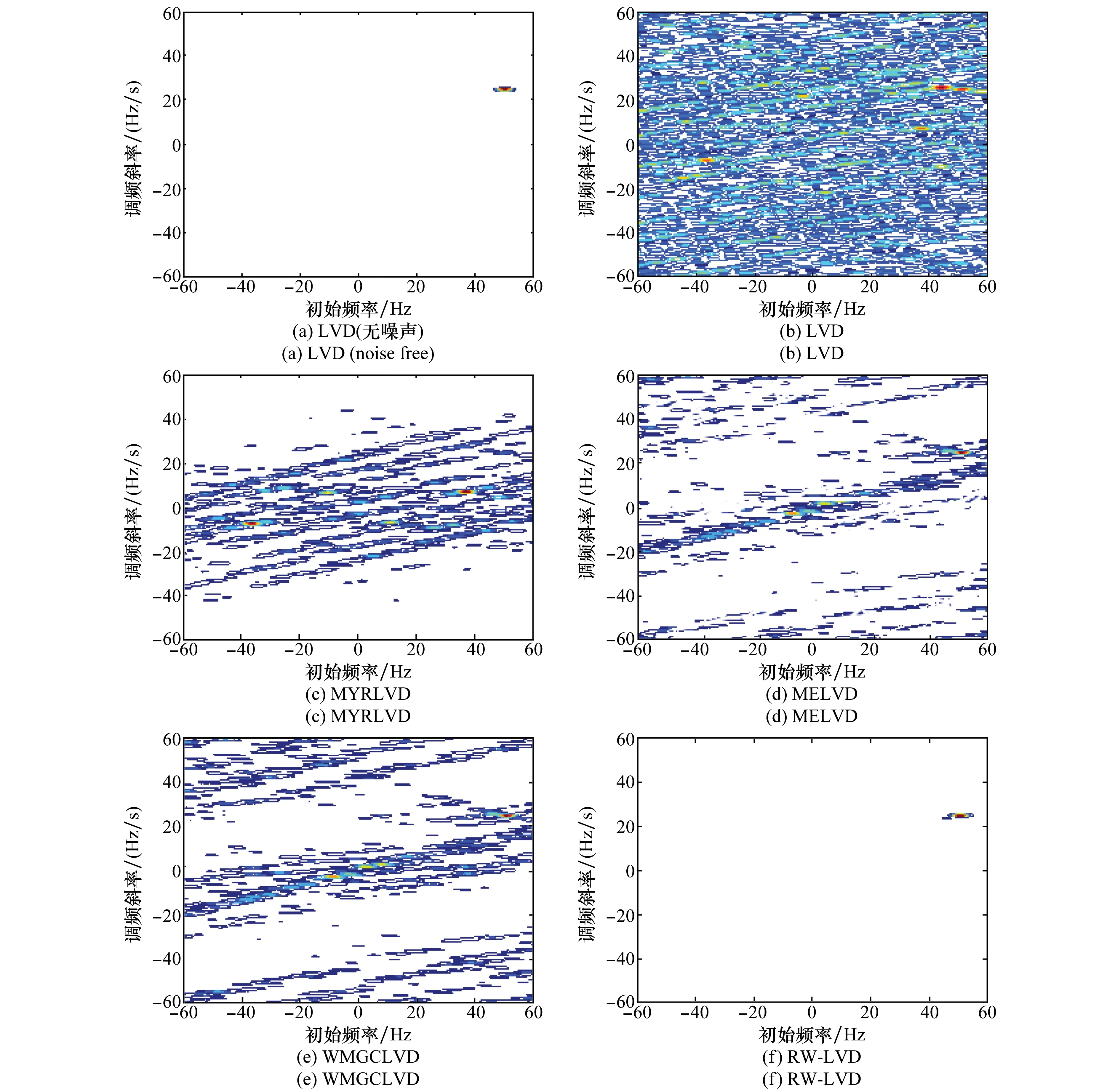
图1 各方法下LVD等高线图Fig.1 LVD contour map of each method
4.2参数估计结果及分析
下面采用所估计参数的归一化均方根误差(normalizedrootmeansquareerror,NRMSE)来比较在α稳定分布噪声下不同参数估计方法的优劣,经过200次蒙特卡罗实验,仿真结果如图2和图3所示。
特征指数α=0.8时,由图2(a)、图2(b)可知,当GSNR≥-7dB时,采用RW-LVD可以准确估计LFM信号的调频斜率和初始频率;GSNR≥6dB时,采用MELVD和WMGCLVD可获得LFM信号的调频斜率,GSNR≥5dB时,可得到LFM信号的初始频率;GSNR≥8dB时,MYRLVD才可得到LFM信号调频斜率和初始频率的准确估计;传统LVD方法受脉冲噪声影响严重,性能严重退化,难以对信号的参数做出有效估计。特征指数α=1.5时,由图3(a)、图3(b)可知,当GSNR≥-12dB时,采用RL可以准确估计LFM信号的调频斜率和初始频率;GSNR≥2dB时,采用MELVD和WMGCLVD;GSNR≥0dB时,采用MYRLVD可得到LFM信号调频斜率和初始频率;传统LVD方法难以实现LFM信号的参数估计。
综上所述,同一GSNR下,RW-LVD比其他方法具有更小的归一化均方根误差,可在较低GSNR下准确估计信号的参数;随着α的减小,各方法的性能都会下降,本文提出的RW滤波新方法则明显优于其他方法。因此,本文提出的RW滤波方法可有效抑制α稳定分布噪声,在较低信噪比下仍具有良好的稳健性。
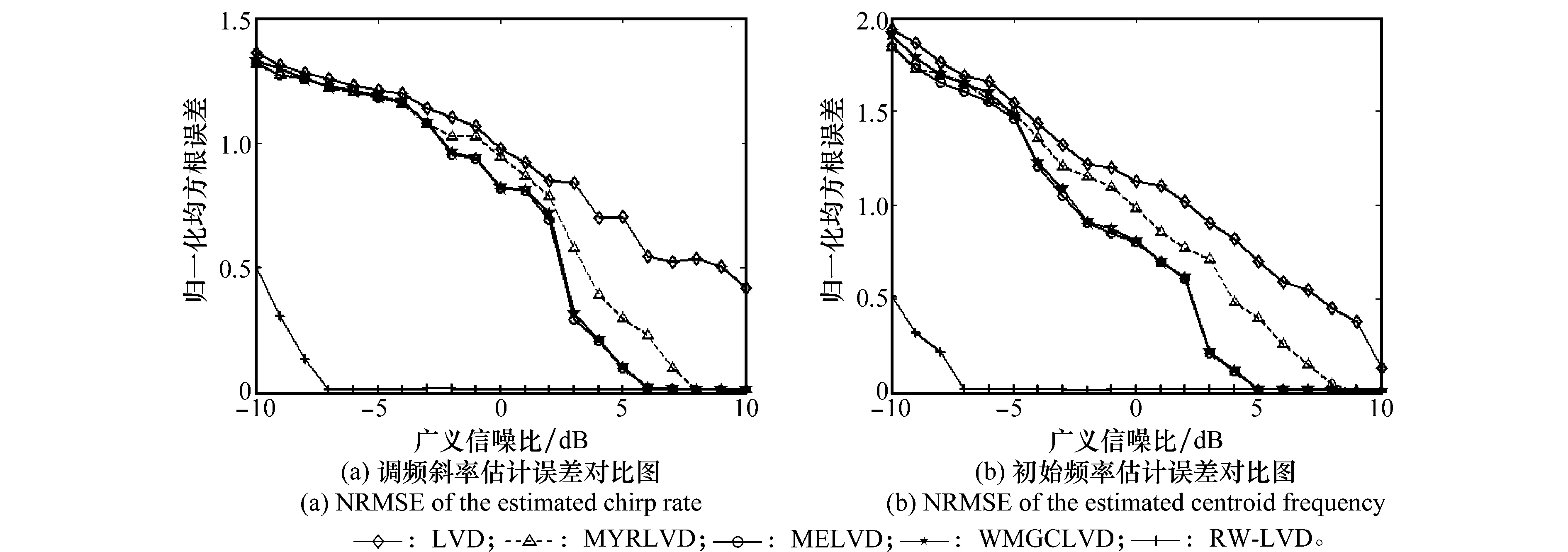
图2 α=0.8时LFM信号参数归一化均方根误差Fig.2 NRMSE of the estimated LFM signal parameters for α=0.8
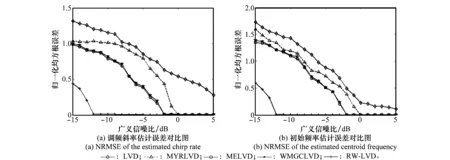
图3 α=1.5时LFM信号参数归一化均方根误差Fig.3 NRMSE of the estimated LFM signal parameters for α=1.5
5 结 论
针对传统加权滤波器在α稳定分布噪声下性能退化的问题,本文从M估计角度出发提出了RW滤波新方法。通过对最大似然估计与M估计分析比较,构造了一种能够有效应用于α稳定分布噪声的代价函数,解决了传统稳健加权滤波器,需获得样本概率密度函数表达式的问题。该方法不仅可有效抑制脉冲噪声,而且构造了一种RW滤波器的统一框架,构建了RW滤波的统一理论基础。仿真实验表明,加权Myriad滤波、加权Merid滤波以及WMGC滤波等多种方法,均可较为有效地对脉冲噪声进行抑制,但在强脉冲噪声下其抑噪性能下降。本文提出的RW滤波方法在强脉冲下也可对噪声进行有效抑制。仿真结果表明,RW滤波方法可有效抑制α稳定分布噪声,从而提高了时频平面分辨率,并获得了较高的估计精度。
[1]LiuMQ,LiBB,CaoCF.Recognitionmethodofdigitalmodulationsignalsinnon-Gaussiannoise[J].Journal of Electronics & Information Technology,2013,35(1):85-91.(刘明骞,李兵兵, 曹超凤. 非高斯噪声下数字调制信号识别方法[J].电子与信息学报,2013, 35(1): 85-91. )
[2]AaloVA,PeppasKP,EfthymoglouG,etal.Evaluationofaveragebiterrorrateforwirelessnetworkswithalpha-stableinterference[J].Electronics Letters, 2014, 50(1): 47-49.
[3]PelekanakisK,ChitreM.Adaptivesparsechannelestimationundersymmetricalpha-stablenoise[J].IEEE Trans. on Wireless Communications, 2014, 13(6): 3183-3195.
[4]ZhongX,PremkumarAB,MadhukumarAS.Particlefilteringforacousticsourcetrackinginimpulsivenoisewithalpha-stableprocess[J].IEEE Sensors Journal, 2013, 13(2): 589-600.
[5]YueBB,PengZM,HeYM.ImpulsivenoisesuppressionusingfastMyriadfilterinseismicsignalprocessing[C]∥Proc.of the IEEE International Conference on Computational and Information Sciences,2013:1001-1004.
[6]BennyMKG,HengSL.SequentialalgorithmsforsampleMyriadandweightedmyriadfilter[J].IEEE Trans. on Signal Processing, 2012, 60(11):6047-6052.
[7]GonzalezJG,ArceGR.WeightedMyriadfilters:arobustfilteringframeworkderivedfromalpha-stabledistributions[C]∥Proc.of the IEEE International Conference on Acoustics, Speech, and Signal Processing, 1996: 2833-2836.
[8]YuanJ,DuSD.ResearchofweightedMyriadfilter[J].Journal of Image and Graphics, 2008,13(7):1287-1291. (袁杰, 都思丹. 加权Myriad滤波器的研究[J].中国图像图形学报,2008, 13(7): 1287-1291.)
[9]KurkinD,RoenkoA,LukinV,etal.Anadaptivemeridianestimator[C]∥Proc.of the IEEE Microwaves, Radar and Remote Sensing Symposium, 2011: 301-304.
[10]KurkinDA,LukinVV,DjurovicI,etal.MeridianestimatorperformanceforsamplesofgeneralizedGaussiandistribution[C]∥Proc.of the IEEE International Conference on Mathematical Methods in Electromagnetic Theory, 2010: 1-4.
[11]ZhaoXM,JinY,JiHB.Parameterestimationoffrequency-hoppingsignalsbasedonMeridfilterinαstablenoiseenvironment[J].Journal of Electronics & Information Technology,2014, 36(8): 1878-1883. (赵新明,金艳,姬红兵. α稳定分布噪声下基于Merid滤波的跳频信号参数估计[J].电子与信息学报,2014,36(8):1878-1883.)
[12]JinY,PengY,JiHB.ParameterestimationofFHsignalsbasedonoptimalkerneltime-frequencyanalysisinαstabledistributionnoise[J].Systems Engineering and Electronics,2015, 37(5): 985-991. (金艳,彭营,姬红兵. α稳定分布噪声中基于最优核时频分析的跳频信号参数估计[J].系统工程与电子技术,2015, 37(5):985-991.)
[13]ZhaiQL,ZhangJ,FuQ.StudyonthetechnologyofLFMpulsecompressionandappliancesinradarsystem[J].Modern Electronics Technique,2007,30(1):17-19(翟庆林,张军,付强.线性调频脉冲压缩技术及其在雷达系统中的应用[J].现代电子技术,2007,30(1):17-19. )
[14]ArceGR,HasanSR.EliminationofinterferencetermsofthediscreteWignerdistributionusingnonlinearfiltering[J].IEEE Trans.on Signal Processing, 2000, 48(8): 2321-2331.
[15]DuanPT.Parameterestimationoflinearfrequencymodulatedsignalsincomplicatednoiseenvironment[D].Xi’an:XidianUniversity, 2014. (段鹏婷.复杂噪声环境中线性调频信号的参数估计[D].西安:西安电子科技大学,2014.)
[16]HuberPJ,RonchettiEM. Robust statistics[M].Hoboken,NJ:Wiley, 2009.
[17]ZhaoCH,MaS.Spectrumsensingbasedonfractalboxdimensionandmyriadfilterunderimpulsivenoise[J].Journal of Vibration and Shock, 2012, 31(3): 84-87.(赵春晖, 马爽. 脉冲噪声下基于Myriad滤波及分形盒维数的频谱感知[J].振动与冲击, 2012, 31(3): 84-87.)
[18]QiuTS,ZhangXX,LiXB,etal. Statistical signal processing non Gaussian signal processing and application[M].Beijing:ElectronicIndustryPress,2004:139-172.(邱天爽,张旭秀,李小兵,等.统计信号处理—非高斯信号处理及其应用[M].北京:电子工业出版社,2004:139-172.)
Unified framework of robust weighted filtering in α stable noise
JIN Yan, HU Bi-xin, JI Hong-bing
(School of Electronic Engineering, Xidian University, Xi’an 710071, China)
In order to solve the problem that the performance of traditional filtering methods degrades significantly inαstable noise environment, a unified structure of robust weighted (RW) filtering is derived based on the M estimation theory, the weighted Myriad and the weighted Merid filtering methods, and accordingly a RW filtering method, i.e., the unified framework, is proposed. The weighted Myriad, the weighted Merid and the generalized Cauchy distribution based weighted filtering methods are interpreted within the unifying framework. The parameters of noisy linear frequency modulation (LFM) signals can be estimated by the Lv’s distribution method based on the RW (RW-LVD) theory, and the estimation results are used to analyze the noise suppression performance. Simulation results show that compared with the weighted Myriad, the weighted Merid as well as the generalized Cauchy distribution based filtering methods, the proposed RW filtering method has better performance and it is robust toαstable noise.
αstable noise; parameter estimation; cost function; robust weighted (RW) filtering
2015-11-03;
2016-05-25;网络优先出版日期:2016-07-05。
国家自然科学基金(61201286);陕西省自然科学基金(2014JM8304)资助课题
TN 911.7
A
10.3969/j.issn.1001-506X.2016.10.01
金艳(1978-),女,副教授,博士,主要研究方向为现代信号处理、统计信号处理、非高斯噪声处理、信号检测与估计、通信信号侦测。
E-mail:yjin@mail.xidian.edu.cn
胡碧昕(1991-),女,硕士研究生,主要研究方向为非高斯噪声下LFM信号处理。
E-mail:15353624268@163.com
姬红兵(1963-),男,教授,博士研究生导师,主要研究方向为光电信息处理、微弱信号检测与识别、医学影像处理。
E-mail:hbji@xidian.edu.cn
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160705.1723.008.html
