变工况下角接触球轴承保持架稳定性分析

姚廷强, 王立华, 刘孝保, 黄亚宇

(昆明理工大学 机电工程学院,昆明　650093)



变工况下角接触球轴承保持架稳定性分析

姚廷强, 王立华, 刘孝保, 黄亚宇

(昆明理工大学 机电工程学院,昆明650093)

复杂变工况条件下旋转机械系统中滚动轴承表现出复杂的动力学特性，更容易产生故障或破坏;考虑间隙碰摩、润滑拖动作用和多体动态接触关系，探索了变工况下球轴承多体接触动力学特性。基于套圈滚道圆环的几何结构方程，建立并实现了运转状态下钢球和套圈的三维接触力学模型和动态接触力的预测搜索算法;考虑钢球和保持架的三维动态间隙碰摩和润滑拖动作用，保持架和引导套圈的等效短滑动轴承的润滑拖动作用，建立球轴承多体接触动力学模型;运用广义-α方法计算分析了变工况下角接触球轴承的动力学特性和保持架运动稳定性，获得变预紧量、变速度、变载荷等工况下球轴承的三维空间运动轨迹、动态作用力、振动加速度及频谱等动力学响应。计算结果表明：内外圈均旋转时，由于启动加速过程中的速度和载荷冲击作用，球轴承存在较大的作用力和振动位移，稳定后的主振频率是自由旋转套圈的转速频率;预紧量的增加，保持架的振动位移仅在内圈受固定径向力作用时明显减小;旋转径向力作用时保持架中心的运动轨迹是近似圆柱面的涡动运动规律。

接触动力学；变工况；保持架；滚动轴承；多体动力学

滚动轴承被广泛应用于航空航天、汽车、工程机械等领域的旋转机械系统。这些关键系统通常在变速度、变加速度、变载荷等典型复杂变工况条件或极端工况条件下工作，表现出复杂的系统动力学特性，滚动轴承更容易产生故障或破坏。变工况下保持架和滚动体的间隙碰撞和摩擦润滑的动力学作用关系复杂，对滚动轴承及其保持架的动力学特性和运动稳定性有着重要的影响[1-3]。变工况下滚动轴承及其保持架的动力学稳定性问题是目前还处于探索阶段和亟待深入研究的系统动力学关键问题，为复杂变工况条件下旋转机械系统动力学分析和动态设计提供一种有效的新方法。

多数文献忽略变工况下轴承的瞬态运动学、动力学特性和钢球与保持架的碰撞摩擦作用，采用拟动力学方法研究轴承的力学特性，逐渐深入分析流体动力润滑和波纹度等因素的影响。对于计及保持架间隙碰撞作用的变工况下球轴承的瞬态运动学和动力学响应的研究，还处于探索阶段。邓四二等[4]在滚动轴承动力学分析理论基础上，建立含轴承零件工作表面波纹度的深沟球轴承动力学数学模型，并以某型号低噪音深沟球轴承为例，对不同结构参数、工况参数及谐波参数下低噪音深沟球轴承的振动特性进行了理论分析。陈小安等[5]应用弹性力学和滚动轴承动力学理论，建立考虑内圈弯曲变形影响的角接触球轴承动刚度分析模型，探讨不同工况下内圈的径向挠度及其对轴承动刚度的影响。方兵等[6]理论计算分析和实验测试了不同预紧力对轴承固有频率的影响。姚廷强等[7]基于套圈滚道的三角网格模型，研究了平稳工况条件下球轴承动力学特性。蔡力钢等[8]针对定压预紧下的角接触球轴承在动态条件下的接触状态进行动力学建模，通过预紧力和转速调整，测量轴承在不同工况下内外圈的相对位移。ASHTEKAR等[9]以离散元方法建立了球轴承力学模型，数值计算和试验测试了不同转速下涡轮增压机轴承的动力学特性和保持架的稳定性。UPADHYAY等[10]研究保持架磨损和不平衡力下滚动轴承-转子系统的非线性拟动力学特性。近年来，保持架的研究通常假设保持架和滚动体间仅存在干摩擦作用，这种假设难以反映轴承运行中流体润滑的动力学特性。刘秀海等[11]研究了滚子和保持架间的拟动力学特性和运动稳定性。陈渭等[12]在基于轴承涡动轨迹假设基础上，建立涡动工况下的轴承滚动体运动学及动力学模型，分析不同外载荷、涡动半径、涡动频率等因素对轴承打滑的影响机理，完成挤压油膜阻尼器轴承的打滑失效分析。梁建波等[13]运用Fokker-Planck接触振动方程，建立二维平面球轴承的等效接触力学模型，仿真分析波纹度对保持架质心的运动稳定性的影响。邓四二等[14]在双列角接触球轴承动力学分析基础上，建立双列角接触球轴承动刚度仿真分析模型，分析轴承结构参数和工况参数对轴承动刚度的影响。姚廷强等[15]运用ANSYS/DYNA仿真分析了平稳工况下角接触球轴承保持架的动态冲击应力和稳定性。

从系统动力学观点出发，考虑间隙碰撞和润滑摩擦作用，钢球、套圈和保持架的三维动态接触关系，建立角接触球轴承多体接触全动力学模型，计算分析变预紧量、变速度变加速和变载荷等工况下球轴承的动力学特性和保持架的运动稳定性。

1　角接触球轴承动态接触关系

为便于和简化计算，对球轴承做以下假设：

① 设轴承各零件为刚体，忽略结构变形，各刚体之间存在局部接触变形；② 根据多刚体动力学理论和罚函数法，考虑等效Hertz接触刚度，以刚体接触对的渗透量来描述轴承各刚体之间的局部接触变形；③ 根据轴承润滑拖动原理，将钢球和套圈滚道、保持架之间的润滑作用，简化为等效的润滑拖动系数和拖动力作用。设保持架和套圈引导面之间为充分润滑条件；④ 除内外套圈同时旋转工况外，假设轴承外圈与机架刚性固定连接，内圈受载荷和转速驱动作用，内圈、钢球和保持架具有6个空间自由度的运动。

1.1广义坐标的选择

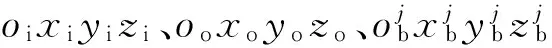
(1)

q=[qiqoqbqc]T

(2)

1.2钢球和套圈滚道圆环的三维动态接触关系

运转状态下球轴承内部存在钢球与套圈滚道的圆环(Torus)的动态接触关系，运用Torus几何结构方程描述套圈滚道的结构参数，从而建立钢球和套圈滚道表面的三维动态接触关系。与套圈滚道的三角网格离散方法相比，套圈滚道的圆环方程直接描述方法可以改善数值计算精度，缩减动态接触的计算规模，有利于系统动力学分析。根据套圈滚道表面的形成原理，球轴承套圈滚道表面是由一个Torus的部分表面构成。由于套圈滚道直径和滚道曲率半径为常数，则套圈滚道上任意为位置矢量可以表示为圆环表面的几何结构参数方程为:

(3)

式中:*为i或o，s*p，s*r和s*t分别为套圈滚道表面任意点的位置矢量，套圈滚道曲率中心的位置矢量和局部圆环面的相对位置矢量。R′i=di/2+Ri，R′o=Do/2-Ro，di，Do分别为内外套圈滚道直径，Ri，Ro为内外圈滚道曲率半径， 0≤φ*≤2π,α≤γ*≤α2，φ，γ分别为钢球方位角(公转角)和内外套圈的沟道角。ξi=-(Ri-(Dw/2))sinα，ξo=(Ro-(Dw/2))sinα为套圈滚道表面的偏置，Dw和α为钢球直径和公称接触角。

图1为钢球与内、外圈的坐标系关系示意图。在惯性坐标系下钢球j与套圈中心的作用关系为:

(4a)

(4b)

图1　球轴承坐标系关系示意图Fig.1　The coordinates of ball bearing

(5a)

(5b)

(6)

由罚函数法可得钢球j与内、外圈滚道的法向接触力为:

(7)

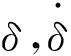
考虑润滑作用，钢球和套圈滚道之间的摩擦力为润滑油的拖动力[17]，可由润滑拖动系数和法向接触力来计算润滑拖动力。

(8a)

(8b)

式中:step(v,0,0,vs,μs)为摩擦因数渐变曲线函数。vs，vd分别为黏滞静摩擦和滑动摩擦的临界速度，μs，μd分别为黏滞静摩擦因数和滑动摩擦因数。

1.4钢球和保持架的三维动态接触关系

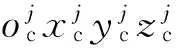
(9a)

(9b)

图2　钢球与保持架的接触力学模型Fig.2　The contact model for balls and cage

对于圆柱型兜孔的保持架而言，在兜孔坐标系下钢球质心与兜孔中心的位置矢量为:

(10)

角接触球轴承中钢球与圆柱型兜孔的间隙为:

(11)

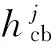
(12)

因此在保持架体坐标系下，钢球与兜孔的法向接触力和切向摩擦力为:

(13)

Fcbt=μcbFcb

(14)

式中：μcb为钢球和保持架兜孔的摩擦因数，由于钢球和保持架兜孔之间的滑动较大，μcb可取为常数。

在SHABERTH的第5代角接触球轴承试验模型基础上引入Hertz接触弹性变形量，可得角接触球轴承中钢球与兜孔的法向作用力。

(15)

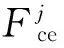
1.5保持架和套圈的等效润滑作用关系

假设保持架和套圈引导面间充分润滑，不存在直接的Hertz接触作用，采用等效短滑动轴承模型来描述套圈与保持架的相互作用。

则外圈与保持架之间的动态趋近量为:

hg=Cg-Δg

(16)

式中:hg为外圈引导面与保持架定心表面之间的动态趋近量，Cg为外圈与保持架的引导间隙的半径量，Cg=(D2-Dc)/2，D2、Dc分别为外圈挡边直径和保持架外直径。Δg为保持架中心的相对位置变化量。

保持架与套圈引导面之间仅存在流体动压作用，而无Hertz接触作用，可将引导面的流体动压作用力等效为短滑动轴承作用力。

(17a)

(17b)

(17c)

式中:Vg为保持架与外圈的相对速度，即为润滑油的拖动速度;Lg为保持架定心表面的宽度，εgc=Δg/Cg为保持架中心的相对偏心率。

由球轴承各零件的动态作用力可以计算出在不同坐标系下的作用力矩，由于篇幅限制，此处省略。

2　动力学模型和求解过程

(18)

式中:

(19a)

(19b)

(19c)

(19d)

首先确定轴承零件的几何结构参数和运动条件的初始值，球轴承各零件由集中质量和惯量描述，套圈滚道由圆环的几何结构方程直接描述。通过各零件的相对位置及运动参数的计算，获得各零件的相互接触时的相对渗透量表达式，由动态接触关系式计算作用在各零件上的作用力和力矩。根据轴承的约束代数方程，运用Matlab软件编制动力学分析的广义-α法[18]，计算约束雅可比矩阵和拉格朗日乘子，轴承零件的新位置和加速度等结果，对变工况下球轴承动力学的微分代数方程组进行积分求解，得到各瞬时点的位置和运动参数，可得变工况下球轴承的动力学结果。

3　球轴承动力学分析实例

3.1计算边界条件

复杂变工况下保持架的稳定性是高速球轴承突然失效的关键问题之一，可能引起高速旋转机械中滚动轴承的动态性能和疲劳寿命相关的严重问题。以球轴承7010C为例，内外圈滚道曲率半径分别为4.65 mm和4.75 mm，节圆直径为65 mm，钢球直径和数目为9 mm和18颗。保持架外径为69.54 mm，内径为65.54 mm，外圈引导的保持架引导间隙值为1.4 mm，兜孔直径为9.2 mm。钢球与套圈的接触刚度为Kci=9.31×105N/mm1.5，Kco=8.09×105N/mm1.5，阻尼参数为0.05 Ns/mm。润滑油动力黏度η0为0.033 Pas，黏压系数α为1.28×10-8Pa-1。计算分析球轴承在① 变速度；② 变预紧量；③ 变载荷等工况下的动力学特性和保持架的运动稳定性。由于篇幅限制，给出球轴承动力学的部分关键计算结果。

3.2变速度下球轴承动态特性

图3～图7分别为外圈中心受Fao=3 000 N预紧力和Fro=2 000 N旋转径向力，外圈自由旋转no=step(time,0,0,0.1,7 200) r/min，内圈固定旋转ni= step(time,0,0,0.05,12 000) r/min下的计算结果。

图3　保持架振动的质心三维轨迹Fig.3　The 3-dimensional trajectory of cage’s center

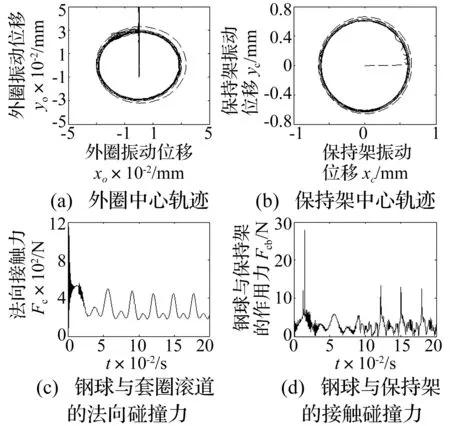
图4　外圈、保持架的质心平面运动轨迹和轴承内部作用力Fig.4　The radial trajectory of outer and cage and internal force of ball baearing

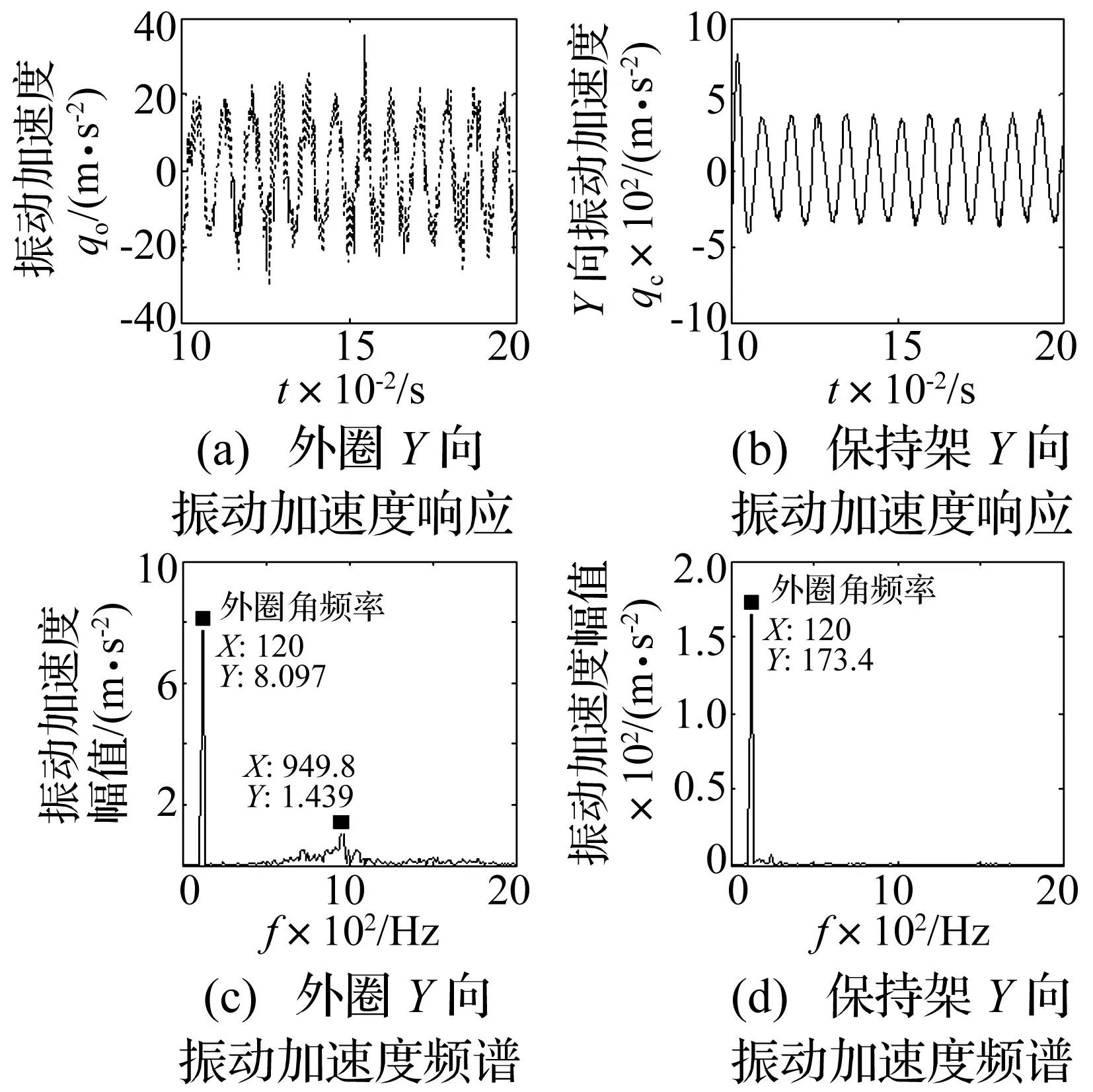
图5　外圈和保持架的振动加速度响应和FFT频谱Fig.5　The acceleration and FFT of vibration of outer and cage

图3为保持架的质心的三维运动轨迹。图4为外圈和保持架的质心平面平面运动轨迹和轴承内部作用力。分析图3可知，保持架中心的运动轨迹在初始启动阶段的0～0.1 s加速过程中存在较大的轴向振动位移，稳定后轴向振动位移较小，保持架质心呈现为以0.078 mm为半径的近似圆柱面三维运动轨迹，轴向振动位移为0.005 mm的微幅波动。图4(a)和图4(b)为外圈和保持架的质心平面运动轨迹。由于启动加速过程中速度和载荷的冲击作用，外圈在初始时存在较大的径向振动位移，稳定后出现出以0.028 mm为半径的近似平面圆周轨迹。图4(c)和图4(d)为球轴承的钢球与套圈滚道的法向接触力和钢球与保持架之间的接触碰撞力。由于旋转径向力、预紧力和离心力的影响，角接触轴承的动态接触力呈现出正弦函数的双峰变化规律，有明显的初始冲击波动(最大值为1 148 N)。由球轴承的间隙碰撞和润滑摩擦作用，稳定运转状态下钢球和保持架之间存在周期变化的拖动力(最大值为7.2N)，同时存在比拖动力大2倍左右的碰撞摩擦力(最大值14.6 N)，初始碰摩力的幅值较大。钢球和套圈滚道的拖动系数和摩擦力矩是动态的变化规律，摩擦力矩(最大值为20.3 N·mm)对钢球的自旋陀螺运动和套圈滚道磨损有着重要的影响。分析表明启动变速度过程、间隙碰撞和润滑摩擦对球轴承内部的动态作用力和保持架的运行稳定性有着重要的影响。

图5为外圈和保持架的振动加速度响应和FFT频谱。外圈振动加速度幅值相对较小，存在949.8 Hz的高频振动响应。保持架振动加速度幅值相对较大，但较为平稳。计算分析结果表明外圈和保持架的主振频率均为自由旋转套圈的驱动转速频率120 Hz(转速为7 200 r/min)，对球轴承的动态响应和运行稳定性有着重要的影响。驱动频率的数值计算结果和理论计算结果是一致的，说明本文轴承模型的计算精度较高。

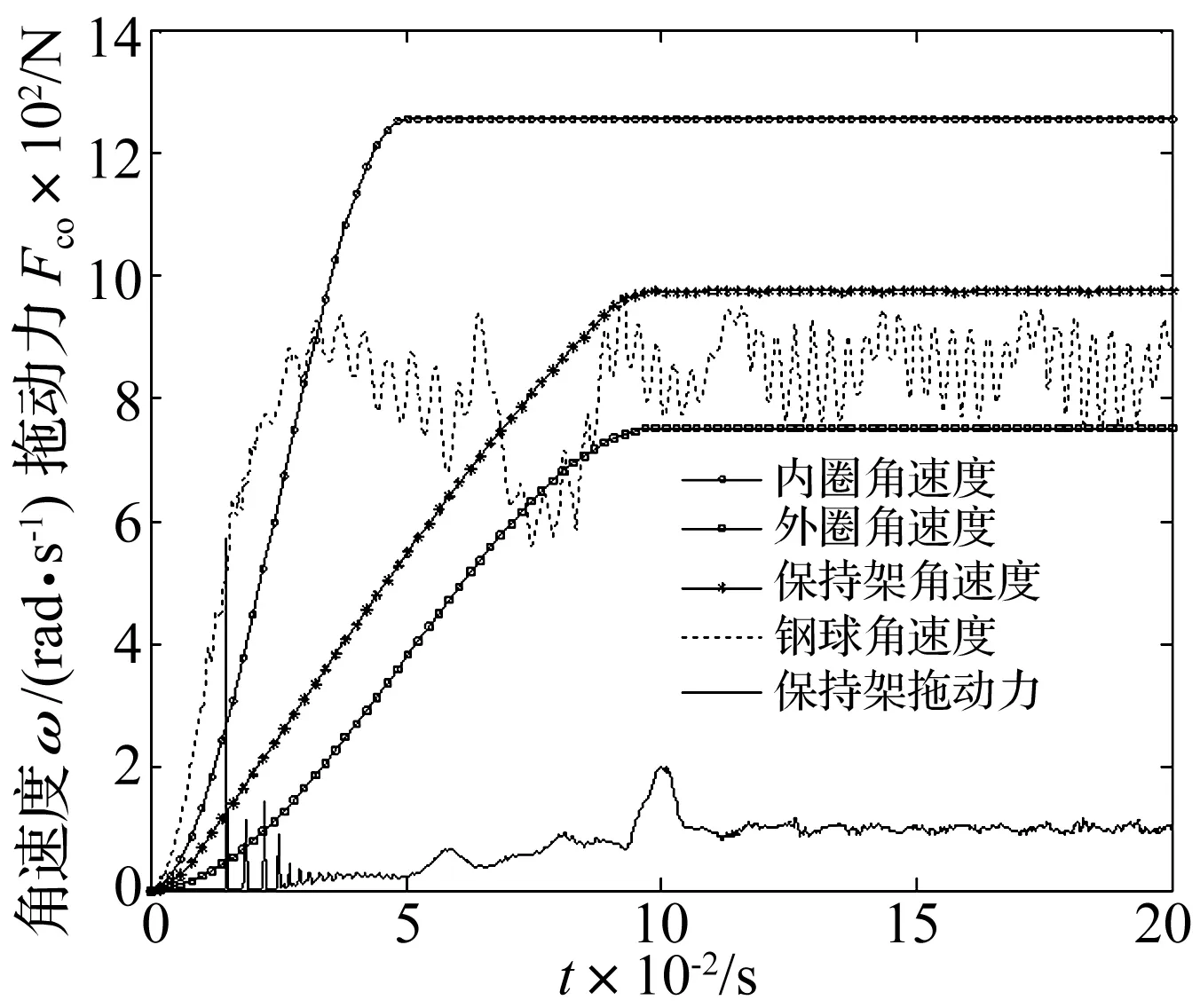
图6　球轴承内部各角速度和保持架拖动力Fig.6　The rule of angular velocity and drag force of ball bearing

图6为球轴承内部各零件的角速度和保持架拖动力。球轴承转速稳定后，保持架的运动角速度和套圈引导面的润滑拖动力较为平稳，保持架的转速为9 315.3 r/min。保持架转速的理论计算值为nc=[ni(dm-Db)+ne(dm+Db)]/2dm=9 267.7 r/min，数值计算结果的相对误差为0.51%，说明本文轴承模型具有较好的计算精度。由于球轴承旋转径向力作用和内外圈同向旋转下，钢球和套圈滚道、保持架兜孔之间存在间隙碰撞和润滑摩擦的空间三维动力学作用关系，从而导致钢球出现打滑现象，其自转转速呈现以±898 r/min波幅的周期变化规律，min=7 223.2 r/min，max=9 019.1 r/min，有效值RMS为7 666.4 r/min。分析可知，启动加速度阶段球轴承运动存在较大的波动，保持架和套圈引导面之间存在较大的冲击润滑拖动力。随着内外转速的增加，拖动力逐渐达到平衡的稳定状态。当内圈在0～0.05 s启动加速至给定转速后，外圈持续加速，拖动力逐渐缓慢增加；在外圈加速至0.1 s达到给定转速时，拖动力存在较大的峰值波动变化，随后重新达到动态平衡的周期稳定变化规律。在内外圈0～0.1 s的启动加速过程中，钢球自转转速波动较大，球轴承的运动稳定性较差。

3.3变预紧量下保持架运动稳定性

图7～图9分别为球轴承外圈固定，内圈中心受Fri=1 000 N旋转径向力或Fyi=1 000 N固定径向力和不同预紧力或预紧位移方式，如图7所示，内圈自由旋转ni= step(time,0,0,0.1,6 000) r/min下球轴承的计算结果。

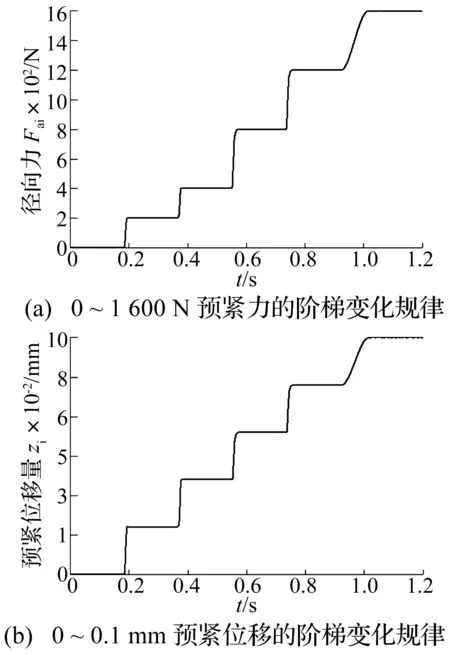
图7　球轴承轴向预紧量的阶梯变化规律Fig.7　The rules of the axial preload conditions of ball bearing

图8分别为不同预紧量下内圈中心的三维运动轨迹和径向平面运动轨迹。图8(a)中预紧力的增加，内圈中心的振动位移逐渐减小，呈现出逐渐上升的径向平面运动轨迹。当内圈中心受旋转径向力和不同预紧方式作用时，图8(b)、图8(c)、图8(d)中内圈中心的径向平面运动轨迹均呈现出近似圆台面的不同变化规律。随着预紧力或预紧位移的增加，内圈中心的振动位移减小，呈现出逐从圆台面的大端变为小端的圆周运动轨迹。对比图8(b)和图8(c)可知，驱动转速对内圈中心运动轨迹的圆台面变化规律有一定的影响，低转速下内圈中心的运动轨迹由大端向小端的变化趋势相对缓慢，圆台面的半径相对较大些。

图9分别为不同预紧量下保持架中心的三维运动轨迹和径向平面运动轨迹。当内圈中心受方向不变的固定径向力和不同预紧方式作用时(图9(a)和图9(b))，保持架中心的三维空间运动轨迹和径向平面运动轨迹是近似圆柱面运动轨迹，且在定位预紧下保持架的运动稳定性相对较差些。随着预紧力增加，保持架中心的径向平面振动位移明显逐渐减小，而随着预紧位移增加，径向平面振动位移仅在预紧位移=-0.1 mm时减小较为明显，其余预紧位移下变化不大，且运动稳定性变差。当内圈中心受旋转径向力和不同预紧方式作用时(图9(c)和图9(d))，在定压预紧下保持架中心的三维空间运动轨迹集中在三个近似圆周轨迹的运动区域内，而定位预紧方式下则是形成近似圆柱面的运动轨迹。计算结果说明预紧力的增加达到一定程度后，对保持架中心的振动位移影响较小。随着预紧力或预紧位移增加，保持架中心的径向平面振动位移的幅值变化不大。在旋转径向力作用下内圈的预紧量增加到一定程度会导致保持架的运动稳定性变差(图9(c)和图9(d))。

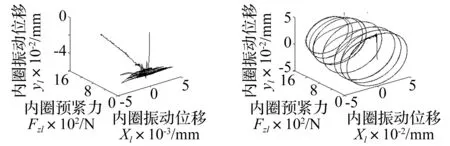
(a)固定径向力Fyi=1000N,预紧力Z1=200～1600N(b)旋转径向力Fyi=1000N,预紧力=200～1600N,低速ωi=1500r/min

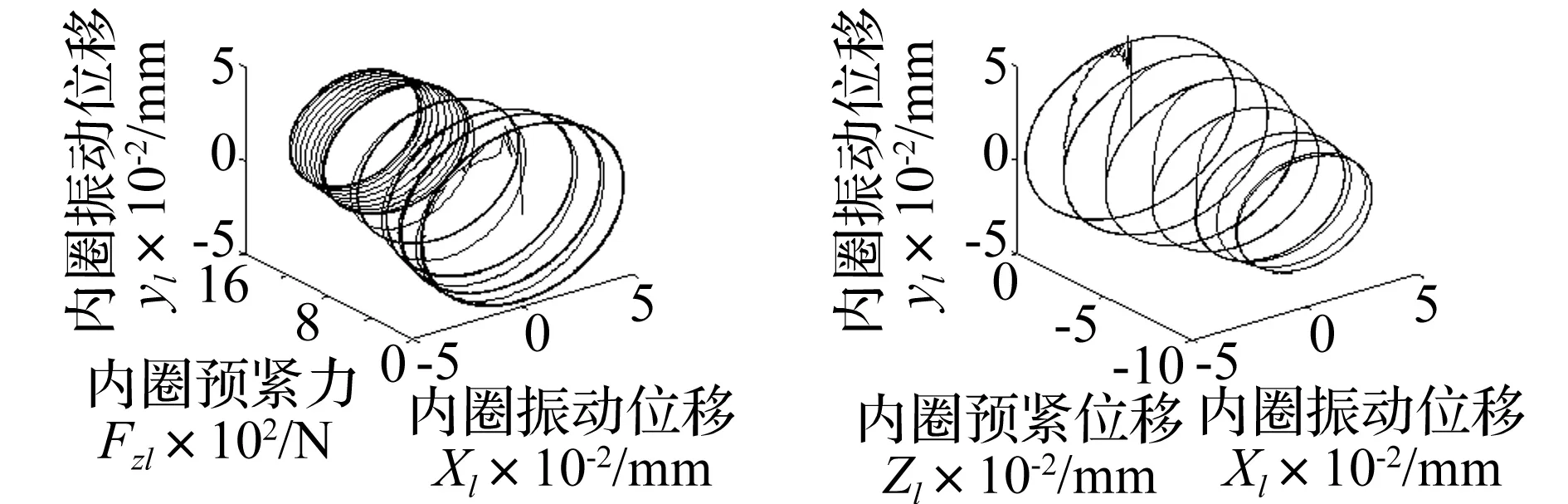
(c)旋转径向力Fyi=1000N,预紧力Z1=200～1600N(d)旋转径向力Fyi=1000N,预紧位移Z1=0～0.1mm,低速ωi=1500r/min图8 不同预紧下内圈中心的径向平面运动轨迹Fig.8Theradialtrajectoryofinnerscenterunderdifferentpreloadconditions

(a)固定径向力Fyi=1000N,预紧力Fzi=200～1600N (b)旋转径向力Fyi=1000N,预紧位移Z1=0～0.1mm

(c)旋转径向力Fyi=1000N,预紧力Fzi=200～1600N (d)旋转径向力Fyi=1000N,预紧位移Z1=0～0.1mm图9 不同预紧下保持架中心的径向平面运动轨迹Fig.9Theradialtrajectoryofcenterscenterunderdifferentpreloadconditions

3.4变载荷工况下动态特性

内圈转速为ni=6 000 r/min；变载荷工况条件如下：① 固定径向力Fyi=0～8 000 N；② 旋转径向力Fri=0～8 000 N；其中变径向力以500 N为基础，以step(…)函数实现等比2倍关系的阶梯递增(见图10)。

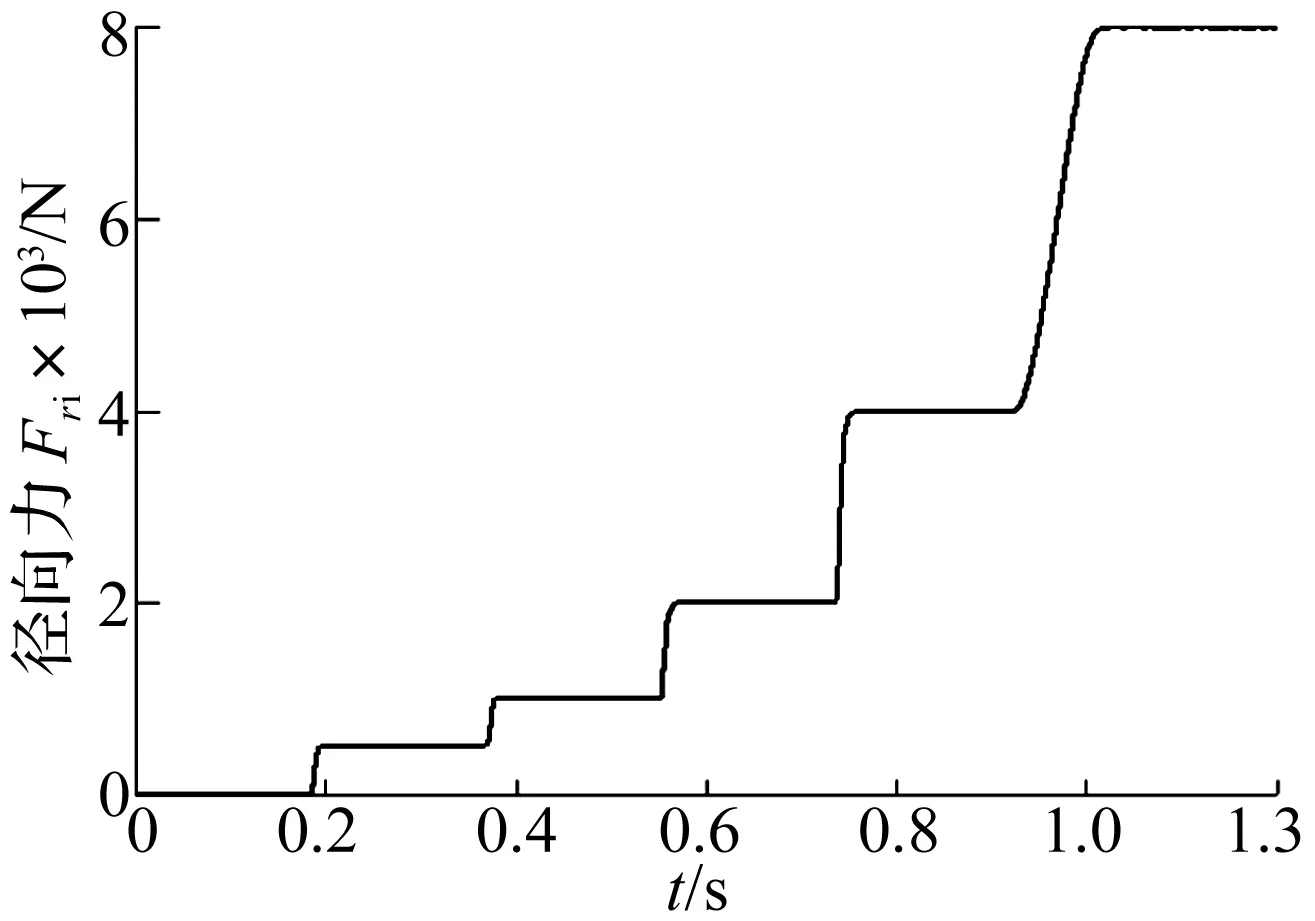
图10　球轴承径向力的阶梯变化规律Fig.10　The rules of the radial load conditions of ball bearing

图11为变载荷对内圈和保持架的中心振动位移的影响。图12为内圈中心的径向平面位移和保持架的三维运动轨迹。分析可知，受固定径向力时(图11(a)和图12(a))，无初始径向力和较小径向力时，内圈中心的振动位移相对较大些，稳定性相对较差。随着固定径向力的增加，内圈中心的振动位移先减小后在径向载荷方向上增加。变旋转径向力时，内圈中心的运动轨迹是圆周运动，且随着径向力的增加，圆周运动的振动位移明显增加，形成三维圆台状(图11(c))或平面圆环状(图12(c))的运动轨迹。径向力的增加对保持架中心的振动位移幅值影响相对较小(图11(b)和11(d))，形成近似三维圆柱面的运动轨迹。受固定径向力时(图12(b))，保持架中心的空间三维运动轨迹为近似圆柱面形态，轴向窜动较小，保持架的运动较为稳定。受旋转径向力时(图12(d))，保持架中心的空间三维运动轨迹为近似圆柱面形态，轴向窜动较大，说明存在频繁的钢球和保持架的间隙碰摩作用，保持架的运动稳定相对较差。

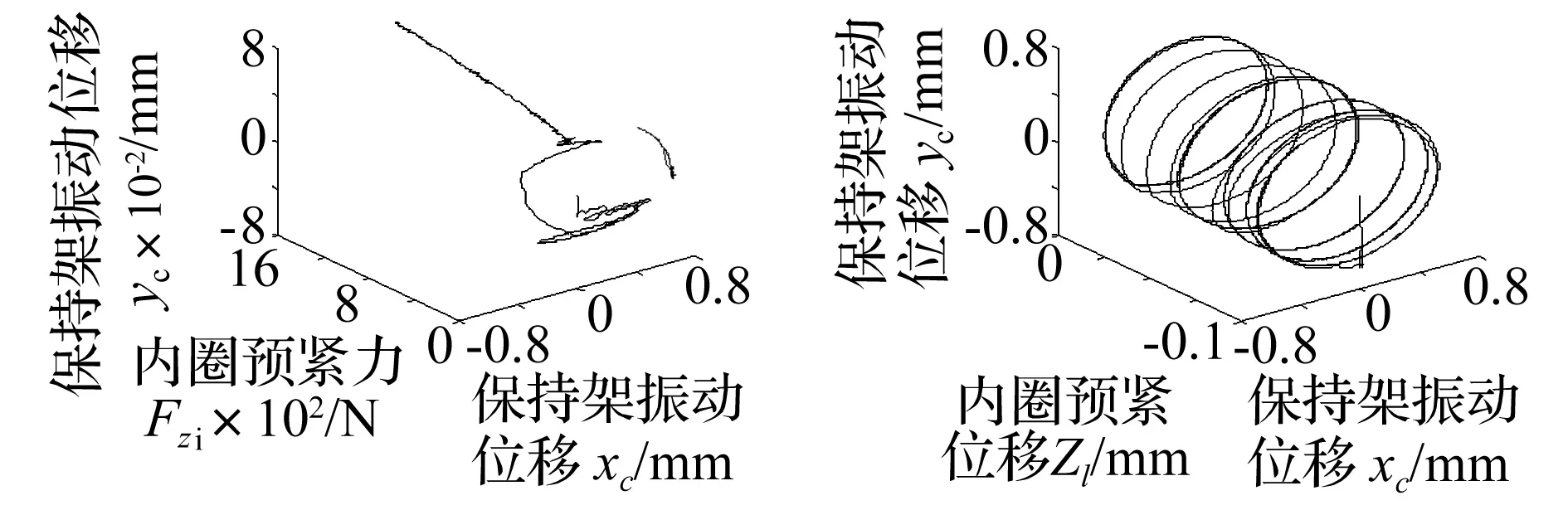
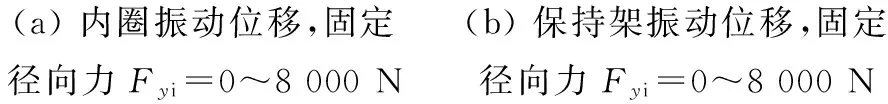
(a)内圈振动位移,固定径向力Fyi=0～8000N(b)保持架振动位移,固定径向力Fyi=0～8000N

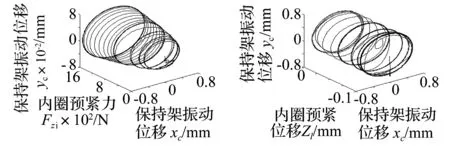
(c)内圈振动位移,旋转径向力Fyi=0～8000N(d)保持架振动位移,旋转径向力Fyi=0～8000N图11 变载荷对内圈和保持架的中心振动位移的影响Fig.11Theruleofvibrationdisplacementsofinnerandcagescenterunderdifferentloads

图13为变载荷对保持架和钢球的拖动力的影响。保持架定心表面和外圈引导面之间存在较大的启动加速阶段的冲击拖动力作用，受旋转径向力时的拖动力幅值(图13(c)中最大值80.6 N)比受固定径向力时(图13(a)中最大值22.4 N)的要大近4倍，而稳定后二者相差较小，同时随着径向力的增加，保持架的拖动力缓慢增加。钢球和套圈滚道的拖动力也存在较大的启动加速阶段的冲击拖动力作用，稳定后受径向力变化的影响较小，且幅值也相对较小。

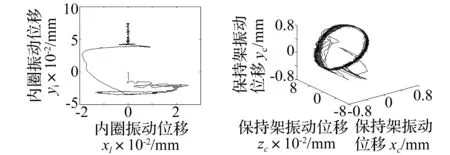
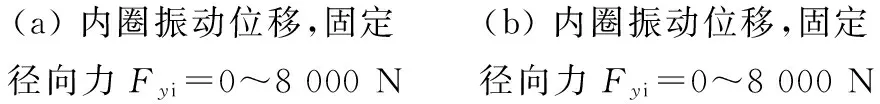
(a)内圈振动位移,固定径向力Fyi=0～8000N(b)内圈振动位移,固定径向力Fyi=0～8000N

(c)内圈振动位移,旋转径向力Fyi=0～8000N(d)内圈振动位移,旋转径向力Fyi=0～8000N图12 内圈中心的径向平面位移和保持架的三维运动轨迹Fig.12Theruleofmotiontraceofinnerandcage

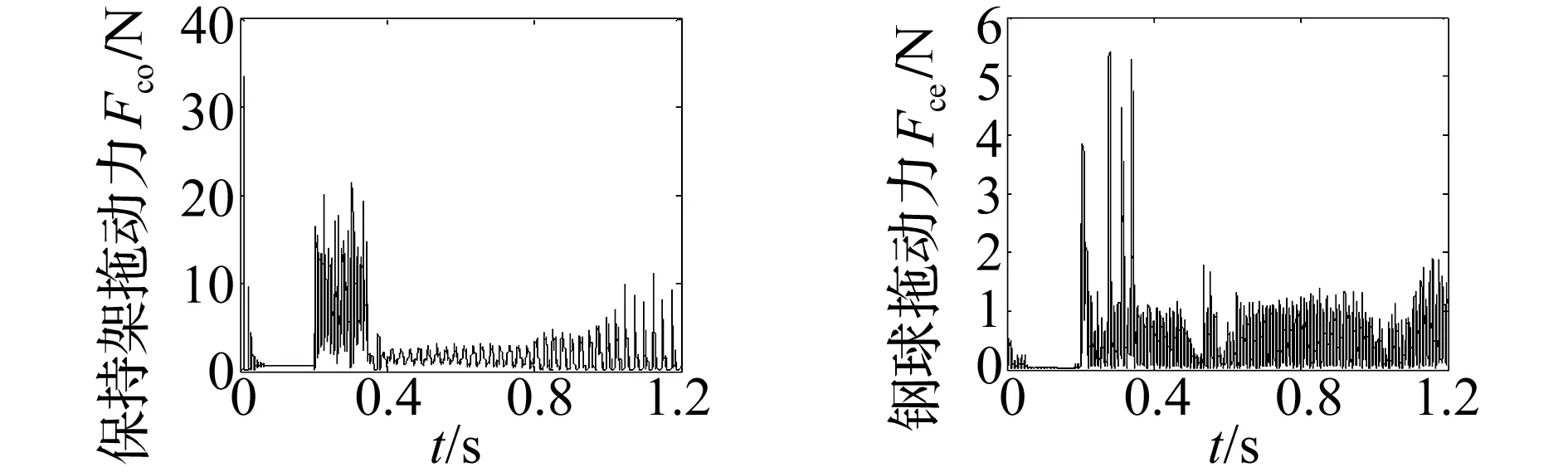
(a)固定径向力Fyi=0～8000N(b)固定径向力Fyi=0～8000N

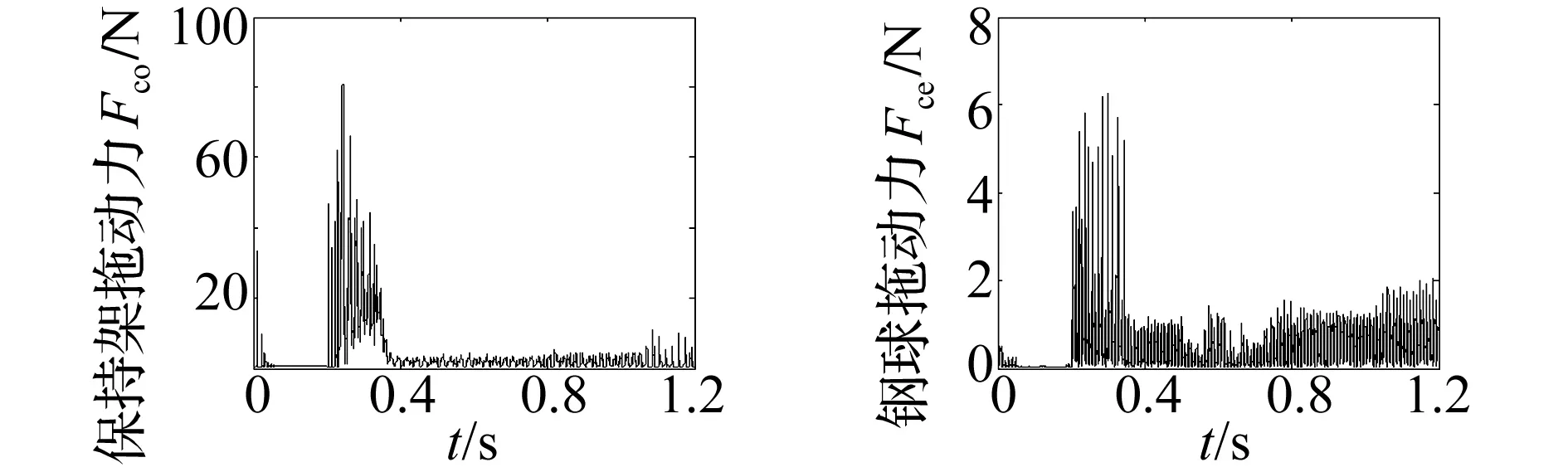
(c)旋转径向力Fyi=0～8000N(d)旋转径向力Fyi=0～8000N图13 变载荷对保持架和钢球的拖动力的影响Fig.13Theruleofdragforceofcageandballunderdifferentloads

4　结　论

变工况条件下考虑间隙碰撞、润滑摩擦作用和多体动态接触关系的球轴承三维全动力学模型更为真实地计算了轴承的动态特性和保持架的运动稳定性，为复杂工况下旋转机械系统中滚动轴承动力学研究和动态设计奠定了理论基础。

(1) 内外圈同向旋转时，由于启动加速过程中的速度和载荷冲击作用，球轴承存在较大的动态接触力和保持架的拖动力，内圈和保持架的振动位移。球轴承稳定后自由旋转套圈的振动加速度幅值相对较小，保持架的振动加速度幅值较大，二者的主振频率均是自由旋转套圈的转速频率。钢球和保持架之间存在明显的间隙碰撞作用，且间隙碰撞力明显大于润滑拖动力，稳定后呈现周期的变化规律。

(2) 定压预紧比定位预紧对振动位移的影响更显著。预紧量的增加，内圈中心的径向运动轨迹为圆台面的变化规律，振动位移减小；保持架中心的径向运动轨迹为圆柱面的变化规律，振动位移仅在内圈受固定径向力作用时明显减小。旋转径向力作用时保持架的运动轨迹是涡动运动规律，预紧量增加到一定程度会导致保持架的运动稳定性变差。

(3) 受固定径向力时，内圈中心的振动位移为窄带的变化规律，且在较小径向力的启动加速过程中存在较大的波动。随着旋转径向力增加，圆周运动的振动位移明显增加，形成三维圆台状或平面圆环状的运动轨迹。保持架中心的运动轨迹在固定径向力下比旋转径向力下要相对稳定些，均呈现出圆柱面的运动轨迹。

[1] 刘保国,孟华.滚动轴承动力学模型研究进展[J].轴承,2014(2):59-64.

LIU Baoguo,MENG Hua. Research progress on dynamics models for rolling bearings[J]. Bearing,2014(2):59-64.

[2] 张建忠, 马国翰.滚动轴承保持架动力学研究进展[J].轴承,2011(1):56-60.

ZHANG Jianzhong，MA Guohan. Research progress oil dynamics of rolling bearing cages[J]. Bearing,2011(1):56-60.

[3] SHAH D S,PATEL V N. A review of dynamic modeling and fault identifications methods for rolling element bearing[C]//2nd International Conference on Innovations in Automation and Mechatronics Engineering.Gujarat ,India: ICIAME,2014.

[4] 邓四二，孙朝阳，顾金芳,等.低噪音深沟球轴承振动特性研究[J].振动与冲击,2015,34(10):12-19.

DENG Sier, SUN Chaoyang, GU Jinfang, et al. Vibration characteristics of low-noise deep groove ball bearings[J]. Journal of Vibration and Shock,2015,34(10):12-19.

[5] 陈小安，刘俊峰，陈宏,等.计及套圈变形的电主轴角接触球轴承动刚度分析[J].振动与冲击,2013,32(2):81-85.

CHEN Xiaoan,LIU Junfeng,CHEN Hong, et al. Dynamic stiffness analysis for motorized-spindle angular contact ball bearings considering ferrule deformation[J]. Journal of Vibration and Shock,2013,32(2):81-85.

[6] 方兵,张雷,曲兴田,等.角接触球轴承动力学建模与实验[J].农业机械学报,2012,43(6):215-225.

FANG Bing, ZHANG Lei, QU Xingtian, et al. Dynamic modeling and experiment of angular contact ball bearing[J].Transactions of the Society for Agricultural Machinery,2012,43(6):215-225.

[7] 姚廷强,王立华,迟毅林,等.球轴承多体接触动力学研究[J].航空动力学学报,2013,28(7):1624-1637.

YAO Tingqiang, WANG Lihua, CHI Yilin, et al. Research on multibody contact dynamics of ball bearings[J].Journal of Aerospace Power, 2013,28(7):1624-1637.

[8] 蔡力钢,杨勇,刘志峰,等.定压预紧下角接触球轴承的动力学建模方法[J].北京工业大学学报,2014,40(5):667-673.

CAI Ligang, YANG Yong, LIU Zhifeng, et al. Dynamics modeling method for angular contact ball bearing under constant preload[J]. Journal of Beijing University of Technology,2014,40(5):667-673.

[9] ASHTEKAR A, SADEGHI F. Experimental and analytical investigation of high speed turbocharger ball bearings[J]. Journal of Engineering for Gas Turbines and Power,2011(12):122501-122515.

[10] UPADHYAY S H, JAIN S C, HARSHA S P. Chaotic dynamics of high speed rotating shaft supported by ball bearings due to distributed defects[J]. International Journal of Engineering Science and Technology,2010,2(10):5746-5764.

[11] 刘秀海.高速滚动轴承动力学分析模型与保持架动态性能研究[D].大连:大连理工大学, 2011.

[12] 陈渭,李军宁,张立波,等.考虑涡动工况的高速滚动轴承打滑失效分析[J].机械工程学报,2013,49(6):38-43.

CHEN Wei, LI Junning, ZHANG Libo, et al. Skidding analysis of high speed rolling bearing considering whirling of bearing[J]. Chinese Journal of Mechanical Engineering,2013,49(6):38-43.

[13] 梁建波,谭晶,黄迪山,等.波纹度对轴承保持架质心稳定性影响的仿真分析[J].轴承,2013(7):5-8.

LIANG Jianbo，TAN Jing，HUANG Dishan, et al. Simulation analysis on influence of waviness on stability for mass center of bearing cages[J].Bearing, 2013(7):5-8.

[14] 邓四二,董晓,崔永存,等.双列角接触球轴承动刚度特性分析[J].兵工学报,2015,36(6):1140-1146.

DENG Sier,DONG Xiao,CUI Yongcun, et al. Analysis of dynamic stiffness characteristics of double-row angular contact ball bearings[J]. Acta Armamentarii, 2015,36(6):1140-1146.

[15] 姚廷强,谢伟,谭阳.角接触球轴承保持架柔性多体动力学分析[J].中国机械工程,2014,25(1):117-122.

YAO Tingqiang, XIE Wei, TAN Yang. Flexible multibody dynamics analysis on cage of angular contact bearing[J].China Mechanical Engineering, 2014,25(1):117-122.

[16] GUPTA P K. Advanced Dynamics of Rolling Elements[M].New York:Springer Verlag, 1984.

[17] 王燕霜,杨伯原,王黎. 4109航空润滑油流变特性的分析及计算[J]. 润滑与密封,2005,167(1):55-60.

WANG Yanshuang, YANG Boyuan, WANG Li.The study of rheological properties of aviation oil no:4109[J]. Lubrication Engineering,2005,167(1): 55-60.

[18] 姚廷强,迟毅林,黄亚宇.柔性多体系统动力学新型广义-α数值分析方法[J]. 机械工程学报,2009,45(10):53-60.

YAO Tingqiang, CHI Yilin, HUANG Yayu. A new generalized-αalgorithms for multibody dynamics[J]. Chinese Journal of Mechanical Engineering, 2009,45(10):53-60.

Dynamic stability analysis on the cage of ball bearing under varying working environment

YAO Tingqiang, WANG Lihua, LIU Xiaobao, HUANG Yayu

(School of Mechanical and Electric Engineering, Kunming University of Science and Technology, Kunming 650093, China)

The dynamic characteristics of rolling bearings in rotating machinery under varying working environment are complex, to which failures and damages are susceptible. Considering the effects of clearance, impact and lubrication on the multibody dynamic contact, the multibody dynamics characteristics of ball bearings under varying working conditions were discussed. A three-dimensional contact dynamics model was established based on the geometric structural equations of ring races, and the searching algorithm for prediction of dynamic contact force was designed. A three-dimensional dynamic model of balls together with the cage was also established with consideration of the clearance, impact and lubrication and the relative action between the cage and guide ring was assumed to be equivalent to a short sliding bearing. Then the multibody contact dynamics model of angular contact ball bearings was constructed and solved by using generalized-α algorithms under varying working conditions. The three-dimensional motion trajectories, dynamic forces, vibration accelerations and FFT spectrums of ball bearings were achieved. In the starting stage, the forces and vibration displacements are larger because of the initial speed and load impact, when the inner and outer rings are both in rotating condition. In the stationary stage, the key vibration frequencies are the angular frequencies of the freely rotating rings. The displacement of cage’s center is deceasing only when the radial force on the inner ring keeps constant. The three-dimensional motion trajectories of cage’s center are approximately the whirling motion of an cylindrical surface.

contact dynamics; varying working environment; cage; rolling bearing; multibody dynamics

国家自然科学基金项目(11462008;11002062)；云南省应用基础研究项目(KKSA20091026)

2015-06-08修改稿收到日期：2015-10-19

姚廷强 男,博士，副教授，1979年生

TB115

A DOI:10.13465/j.cnki.jvs.2016.14.028