基于切削动力学及其不确定特性的数控机床结构参数分析优化

黄　华， 张树有， 何再兴， 裘乐淼

(1.兰州理工大学 机电工程学院，兰州　730050； 2.浙江大学 流体动力与机电系统国家重点实验室, 杭州　310027)



基于切削动力学及其不确定特性的数控机床结构参数分析优化

黄华1， 张树有2， 何再兴2， 裘乐淼2

(1.兰州理工大学 机电工程学院，兰州730050； 2.浙江大学 流体动力与机电系统国家重点实验室, 杭州310027)

针对传统数控机床结构设计中较少考虑切削动力学及其不确定特性的问题，提出了基于切削动力学约束和不确定因素的影响，根据目标切削深度对结构进行优化设计的方法。分析切削动力学特性，根据颤振频率分布和整机模态实验确定限制切深的关键部件，以其外部轮廓壁厚和内部筋板壁厚为对象，进行参数灵敏度分析以确定设计参数。将最小临界切削深度与目标切削深度的差值转化为结构动柔度的修改量，在质量、静刚度等条件的约束下，通过对局部结构的修改，在保持质量基本不变的情况下，满足了生产率要求的目标切削深度，并以一台数控加工中心的结构优化设计为例进行了验证。

切削动力学；不确定性；动柔度；最小临界切深

金属切削加工需要保证一定切削深度以满足生产率要求，而机床能达到的稳定切削深度受制于机械结构和加工工艺复杂的耦合作用。因此，为了充分发挥机床的性能，需要在设计阶段从结构动力学和切削动力学方面对机床结构进行优化设计。

众多学者在这方面展开了研究，文献[1]应用权重分配准则，给床身上不同承载区域的重要性赋予不同的权重，优化床身内部筋板和外支撑板的布局方式和板厚，减轻重量的同时改善了其承载情况。文献[2]采用响应面模型，以部件的板厚为设计变量，对一台立式加工中心进行了动、静态和轻量化多目标优化设计。文献[3]通过实验辨识出机床整机动刚度薄弱环节，以立柱结构为优化对象，运用灵敏度分析法计算出立柱质量和固有频率对各个壁板的灵敏度，通过修改壁板厚度提高了整机动刚度并减轻了重量。文献[4]探讨了移动部件轻量化对于节能的意义。还有学者从结构仿生或者材料仿生的角度对机床的承载部件或者移动部件进行优化设计[5]。这些方法一般是从结构动力学的要求出发，关注其低阶固有频率、动刚度、模态匹配或者切削频率禁区等指标，较少考虑切削动力学的需求[6]。不合理的切削动力学特性轻则导致高性能机床不能充分发挥其功能，重则导致安全事故发生[7]，忽略切削动力学的影响往往不能取得预期效果，因此，在结构动力学优化的基础上，有必要从切削动力学的角度来优化机床的设计。文献[8]利用切削颤振理论，根据颤振频率找出对应的模态，并通过设置加强筋提高该模态对应的固有频率和动刚度以改进。文献[9]考虑结构修改的可行性，提出了一种在主轴外径上附加质量以减小传递函数的实部，从而提高了切削的极限深度。文献[10]通过切削稳定性图建立了机床结构和工艺的数学模型，该模型识别了影响切削效率的设计参数，针对结构进行改进设计或者针对已经制造的样机附加阻尼以提高切削效率。文献[11]针对相关参数的不确定性获得了稳健的切削稳定性曲线，以此指导切削工艺参数的选择。

对于铸铁或者钢材等较硬材料的粗加工、半精加工，切削稳定性主要取决于机床结构基础支承系统的动力学特性[12]，由于机床加工位姿、测试条件或者制造、装配的差异、服役性能的退化，动力学特性会有一定的不确定性。另外，对于特定的加工工艺来说，其切削参数也有一定的不确定性，包括加工材料特性、工艺参数的波动，按照确定性数值进行稳定性分析会有较大误差。因此，本文考虑不确定参数对机床切削稳定性的影响，并将实际切削能力与目标切削能力的差异转化为结构修改的定量指标，采用灵敏度分析方法确定设计参数，考虑质量、静刚度等指标的约束，对机床结构进行优化设计。

1　切削动力学及其不确定性分析

切削动力学特性由切削工艺和机床结构性能决定，本文分析工艺和结构参数对切削动力学的影响，根据各因素与切削深度的关系，找出各因素组合下的最小极限切削深度，将该深度与切削效率要求的最小切削深度比较，根据两者的比例关系以及质量、刚度条件的约束对结构参数进行修改，保证切削深度满足生产率指标要求。

1.1临界稳定切削深度

根据切削颤振理论，铣削加工系统的临界稳定切削深度aplim可表示为：

(1)

式中：ωc为颤振频率;T为刀齿切入周期;Kt为切向切削力系数;z为刀具齿数;Λ为闭环动态铣削力特征方程的特征值。特征方程可表示为：

a0Λ2+a1Λ+1=0

(2)

式中：

a0=ΦxxΦyy(αxxαyy-αxyαyx)；

a1=αxxΦxx+αyyΦyy

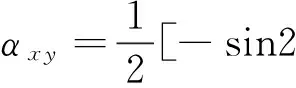
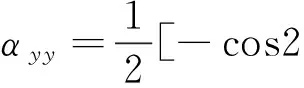
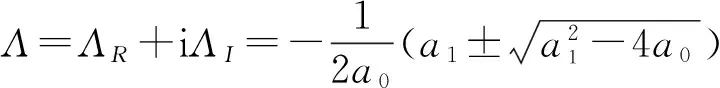
式中：ω、k、ξ、φst、φex分别为固有频率、模态刚度、阻尼、切入角、切出角。式(2)表明，临界切削深度主要取决于方向因子αxx、αxy、αyx、αyy和切削区域的传递函数Φxx、Φyy，这两项主要由切削工艺参数和刀具-工件系统的模态参数决定。

1.2切削动力学不确定性影响因素分析

一般的切削稳定性叶瓣图见图1。由图1可知，底下的水平线表示最小临界切削深度，水平线以下是无条件稳定区，叶瓣内的区域是不稳定切削区，代表最小临界切削深度的水平线和两相邻叶瓣包围的区域是有条件稳定切削区。为了满足生产率的要求，保证在任意转速下的稳定切削深度都处在无条件稳定切削区，需要通过结构设计提高最小临界切削深度，即将最小临界切削深度所在的水平线提高到目标切削深度的位置。

图1　切削稳定性叶瓣图1Fig.1　Cutting stability lobes 1

1.2.1工艺参数的影响

从工艺参数的角度看，切削稳定性公式表明切削深度受刀具径向浸入比、刀具齿数、切削力系数、加工转速的影响。其中，切削力系数包括切向切削力系数和径向切削力系数，前者与极限切深成反比，后者与前者的比值决定了方向系数。最小临界切削深度随着刀具径向浸入比的增加而下降，刀具齿数和加工转速决定了激励频率。对于常见的几种材料，文献[13]提供了几种切削力系数，最小临界切削深度随着切削力系数的增加而下降。

1.2.2模态参数的影响

系统传递函数的影响因素众多，包括所受外界激励、系统结构参数中质量、刚度、阻尼及振型、固有角频率ω和阻尼比ζ等，主轴-刀柄-刀具结合部的动力学特性和高速旋转引起的陀螺力矩、离心力对系统切削稳定性的影响也不容忽视[14]。根据式(2)，本文重点研究结构的固有频率、模态刚度、阻尼对切削稳定性的影响。模态数据见表1。

表1　工艺系统模态参数

令表1中各参数分别在初值的50%～200%范围内变化，将数据代入式(1)、式(2)进行计算，得到各参数对切削稳定性的影响见图2，图2中纵坐标为最小临界切削深度；横坐标为各参数与其初值的比值，其中ωn0、k0、ζ0分别代表固有频率变化的比值、模态刚度变化的比值、阻尼比的初值。

图2　模态参数与最小临界切削深度的关系Fig.2　Relation between modal parameters and minimum critical cutting depth

由图2可知，固有频率对最小临界切削深度的影响较小，模态刚度、阻尼比对最小临界切削深度的影响较大，两者为正比例关系。

综上分析，在最小临界切削深度的各项影响因素中，阻尼比系数、刚度系数、固有频率、切削力系数和径向切削浸入比都有不确定性，为了保证机床在一定工艺范围内稳健的满足给定的目标切深，需要根据目标切深和实际值的差异，对机床结构进行优化设计。

2　考虑切削特性的结构参数分析与优化

2.1切削深度和结构参数的关系分析

根据切削稳定性理论分析可得到系统的颤振频率，因为颤振频率一般发生在机床结构的某阶固有频率附近[15]，由模态实验可确定该频率对应的模态振型，从而确定振型的对应部件。由模态振型的正交性可知，当机床在第r阶固有频率ωnr附近振动时，如果各阶模态耦合不紧密，则结构的频响特性主要决定于第r阶模态，其余各阶模态的影响可忽略，因此可将各阶模态视为单自由度系统研究其振动的稳定性。根据振动力学，对于第r阶模态，有：

(3)

(4)

由图2可知，当ξr不变时，模态刚度与最小临界切削深度为线性比例关系，又因为结构阻尼主要决定于结合部的联接情况，所以对于小范围内的结构修改而言，ξr保持不变，由式(4)可知模态刚度与动柔度成反比。

设该机床实际最小临界切深aplim与目标要求的最小临界切深agoal之比为p，则有：

(5)

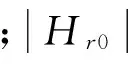
2.2基于结构灵敏度的优化过程建模分析

对系统的动柔度进行优化设计需要考虑两个方面约束：①机床刀尖点的静变形必须在许可范围内，因为沿切削力方向的变形最大，所以以该方向的变形为约束，优化设计后对其它两个方向的变形进行校核；②结构的质量改变尽可能小。由此建立多目标优化模型：

(6)

式中：H和ΔH分别为该模态的最大动柔度和动柔度的目标修改量;δsz、δsx、δsy分别为刀尖点在z、x；y方向的静变形；δsz0、δsx0、δsy0分别为各方向允许的最大静变形。Δtil、Δtiu分别为设计参数变化的上、下限;n为参数个数。因为严格的质量恒定限制了系统尺寸的寻优，因此令质量m的变化Δm在初始质量m0的2%的范围内，在该范围内仍视为质量恒定。

按照上述模型进行优化时，需要计算目标参数和设计参数之间的关系，但是结构动柔度、静变形与设计参数之间无显式的函数关系，所以本文采用试验设计确定设计参数，然后通过有限元计算获得设计参数对应的目标参数，包括结构动柔度、静变形，将对应的几组设计参数和目标参数拟合为二次函数关系式。以动柔度为例，设通过有限元分析得到结构相关尺寸增量与目标对应的数值关系，并对其进行二次函数拟合，得到的函数关系式为：

i=1,2,…,m

(7)

式中:ai、bi、ci为函数系数。

该函数对各尺寸参数的灵敏度表示为：

i=1,2,…,m

(8)

用矩阵形式可表示为：

Sh=AΔt+B

(9)

z方向是主要的受力和变形方向，为减小计算量，以z方向的静刚度为约束条件，再根据优化结果对另外两个方向的变形进行校核。令z方向的静刚度与设计参数的关系式为：

i=1,2,…,m

(10)

式中：di、gi、fi为函数系数。其灵敏度矩阵为：Sδ=DΔt+G。质量灵敏度为：

Smi=ρqi

(11)

式中：ρ为结构材料的密度；qi为尺寸参数ti对应的表面积。令qi的集合为Q，则动柔度、变形、质量与设计参数之间的关系为：

因此，根据试验设计得到的数据拟合出系数矩阵A、B、C、D，并求出各参数对应的表面积的集合Q，将式(12)并与式(6)联立，便可求得各参数的最优解。

2.3考虑切削特性的结构参数分析优化流程

提出了一种基于切削动力学不确定性的数控机床结构优化设计方法流程。建立机床有限元模型并根据模态实验结果对有限元模型进行校正。根据刀具-工件系统的频响函数实验结果，进行切削稳定性仿真获得系统的颤振频率，结合整机模态实验确定引起颤振发生的主要模态。如果该模态的应变能主要由某些导轨提供，可以通过加强导轨联接部进行强化；如果主要是由部件提供，则通过调整筋板、壁板厚度等措施修改该模态，本文主要针对部件的结构参数进行调整。在修改过程中，应用灵敏度分析确定修改参数，在质量、静刚度等条件的约束下，通过修改模态动柔度以缩小稳定性切削深度和生产率要求的切削深度为目标，反复迭代直到接近切深目标为止。在修改过程中，按照一般的设计需求，将设计参数按照5的倍数进行调整，具体流程见图3。

3　实例分析

某机床企业需要开发一台卧式加工中心，主要面向柴油发动机缸体的加工，缸体材料为铸铁。其刀库有>40把刀具，包括各种面铣刀、立铣刀20把。其耗时最多的工序为某表面的粗加工和半精加工，为满足生产率，要求在该工序时，以任意浸入比和任意进给方向，不论使用何种冷却条件，最小的临界切削深度能保持在>3 mm。现根据前述理论分析，从切削动力学的角度对该机床进行优化设计。

3.1切削动力学分析

该机床使用的最大刀具直径为160 mm，刀齿数为8，最小刀具为直径40 mm，刀齿数4。最小切向切削力系数Ktc=1 203.1 N/mm2，最大切向切削力系数2 193 N/mm2；最小径向切削力系数Krc=2 121 N/mm2，最大切向切削力系数3 309 N/mm2。采用锤击法对刀具及工件进行激励实验，采用加速度传感器获取结构的动态响应，通过B&K 公司的7700 Pulse多通道动态信号采集分析系统来记录分析数据。实验仪器和现场条件见表2。

图3　基于切削动力学特性的机床结构优化设计流程图Fig.3　Flow chart of optimization design for machine tools based on cutting dynamics

表2　主要测试仪器

刀具与工件系统的频响函数测试现场见图4。

图4　刀具-工件系统频响函数测试Fig. 4 Testing of frequency response function of tools and workpiece

经数据处理软件识别后得到系统前六阶模态参数见表3。

因为模态参数有一定范围内的波动，因此令各参数在其初值10%的范围内变化。根据前述分析，取使临界切削深度最小的各参数的组合，即刀具为直径40 mm，刀齿数4，槽铣；最大的切向切削力系数2 193 N/mm2和最大的径向切削力系数3 309 N/mm2，固有频率取初始值，阻尼比和模态刚度取最小值，进给方向与机床坐标系X轴方向重合，根据以上参数，仿真获得的稳定性叶瓣图见图5。

表3　系统模态数据

图5　切削稳定性叶瓣图2Fig.5　Cutting stability lobes 2

由图5可知，最小临界切削深度1.39 mm，最大临界切削深度3.92 mm。相差将近3倍。可见，工艺参数和模态参数的不确定性对临界切削深度有很大影响。根据工艺要求，最小临界切深aplim与目标要求的最小临界切深agoal之比p为：

(13)

另外，仿真得到的颤振频率见图6，表明颤振频率分布在120～200 Hz之间。

图6　切削颤振频率分布Fig.6　Chatter frequency

3.2整机模态实验

在仿真获得了颤振频率的基础上，需要通过模态实验分析该频率对应的结构部件。为了获得相对准确的模态实验结果，对本机床同系列的另一台结构相似的机床，在主要部件装配完毕但还未安装防护的情况下进行模态实验分析。所使用的仪器与表1相同，实验现场见图 7(a)。采用单点激励多点响应的方法，用力锤沿水平方向对主轴端进行激励，每次连续敲5下，使用3个加速度传感器在x、y、z三个方向依次对主轴部件、立柱、工作台、底座中间块和床身等进行响应测量，传感器布置和各测点编号见图 7(b)。使用数据采集系统BK自带的pulse软件获取完整的频响函数，经ME′scope分析软件处理后得到各阶振型见图 7(c)，实验结果见表4。

对比图6的颤振频率分布和模态实验结果，可知第6阶振型-立柱的高阶扭摆是该机床切削深度的薄弱环节。根据式(13)，为满足目标切削深度的要求，需要对该模态进行强化设计，使修改后刀尖点的动柔度降低≈2.16倍。

表4　机床模态实验结果

3.3立柱结构参数分析优化

立柱结构尺寸见图8，立柱内部采用米字形筋板，这是最具抗扭能力的一种筋板形式。筋板上开有减重孔，设计参数的选取见图8和表5。

图7　机床模态实验Fig.7　Machine tool modal experiment

图8　立柱内部结构和尺寸参数Fig.8　Internal structure of the column and dimensions

表5　变量数值范围

将简化后的机床模型导入workbench中，并将各相关参数设为变量，在机床刀尖点施加简谐力，以整体结构第6阶模态的动柔度为目标，通过改变各相关参数，计算得到尺寸变量和动柔度的关系见表6。

按式(7)对以上数据进行二次函数拟合，得到各尺寸增量与动柔度的函数关系式：

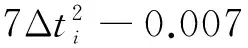
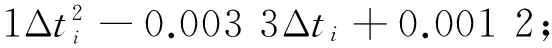
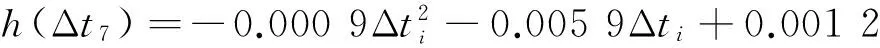
按式(8)，动柔度对各尺寸参数的灵敏度表示为：

sh1=-0.002 8Δt1-0.001 6;

sh2=-0.001 8Δt1-0.003 8;

sh3=-0.001 8Δt1-0.003 8;

sh4=-0.000 6Δt1-0.001 2;

sh5=-0.003 4Δt1-0.007 7;

sh6=-0.002 2Δt1-0.003 3;

sh7=-0.001 8Δt1-0.005 9。

按式(9)，用矩阵形式表示为：Sh=AΔt+B，其中：

B=-10-3×[1.6　3.8　3.8　1.2　7.7　3.3　5.9]T

根据工艺条件，在粗加工条件下，最大切削力为5 000 N，要求各方向上刀具和工件的相对位移不超过200 μm。为机床主轴上施加三方向的最大切削力Fx=Fy=Fz=5 000 N，承受主要切削力的方向为z方向，计算得到设计参数与z方向的静变形的关系见表7。

表7　尺寸变量与静变形的关系

同理，其灵敏度矩阵为：

G=-10-3×[8.28 7.30 4.38 2.28 13.44 6.32 7.30]T

另外，立柱材料为灰铸铁，密度ρ=7.29×103kg/m3，根据式(11)得到立柱质量与各参数的灵敏度关系为：

Sm=[10.69.41.24.15.8-1.5-1.7]

将矩阵A、B、D、G和Sm代入式(12)，并与式(6)联立，又因为Δh为负，对其取绝对值，得优化模型为：

(14)

在Matlab软件中求解式(14)，得到一组解：

Δt=(5,-5,5,-10,10,10,20)T

对修改后的模型重新进行谐响应分析(见图9)。由图9可知，仿真结果比实验结果稍有偏大，同时，优化后的结构第6阶动柔度从12.2 μm降低到6.6 μm。

将优化后的模型在有限元软件中进行更新并计算(见表8)。其中立柱质量减小了31 kg，同时各方向静刚度满足要求。

假设修改前后的阻尼比参数保持不变，根据模型修改后重新分析得到的模态参数进行稳定性仿真，得到的稳定性叶瓣图如图5中的“结构优化后的临界切削深度”所示，其最小临界切削深度为2.91 mm，已经接近目标切削深度3 mm。可见，结构修改达到了目的。

表8　立柱结构尺寸优化前后的对比

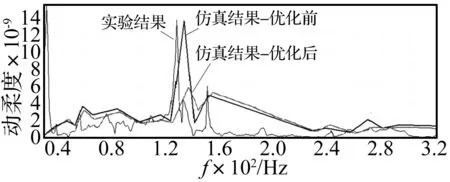
图9　谐响应分析结果Fig.9　Results of the analysis of harmonic response

4　结　论

仅从结构动力学角度对机床进行优化设计或者在加工阶段对工艺参数进行优化，难以实现高效、稳定的切削加工。本文考虑切削动力学及其不确定特性，对机床结构参数进行了分析优化研究，主要工作与特点有：

(1) 从结构动力学参数和工艺参数两方面分析了切削动力学的不确定性影响因素，将不确定因素组合得到的最小临界切削深度与目标切削深度的比值转化为结构动柔度的比值，以此作为结构参数优化设计的定量指标，克服了设计修改的盲目性。

(2) 根据切削稳定性仿真获得机床的颤振频率图，与实验模态分析获得的各阶模态可视化振型比较，结果表明制约机床切削性能的主要因素是第6阶模态(131 Hz)；振型表明该模态可通过调整相关部件筋板的或壁板的厚度进行改善。从而明确引起机床切削性能降低的结构设计上的不足，并通过对机床结构的调整来实现切削性能的优化。

(3) 采用灵敏度分析方法，以结构动柔度为修改目标，结合质量和静刚度等指标的约束，对机床进行切削动力学的优化设计。将本文的方法应用在一台加工中心的结构优化设计上，针对该机床制约切削性能的薄弱环节——立柱，从内部筋板和外部壁板的厚度进行优化，结果表明本文的方法是可行的。

[1] LIA B, HONGA J, WANG Z. Optimal design of machine tool bed by load bearing topology identification with weight distribution criterion[C]// 45th CIRP Conference on Manufacturing Systems,2012:626-631.

[2] 姜衡, 管贻生,邱志成,等. 基于响应面法的立式加工中心动静态多目标优化[J].机械工程学报,2011,47(11):125-133.

JIANG Heng, GUAN Yisheng, QIU Zhicheng, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11):125-133.

[3] 郭垒，张辉，叶佩青，等. 基于灵敏度分析的机床轻量化设计[J]. 清华大学学报(自然科学版),2011,51(6):846-850.

GUO Lei, ZHANG Hui, YE Peiqing, et al. Light weight design of a machine tool based on sensitivity analysis[J]. Journal of Tsinghua University(Science & Technology), 2011,51(6):846-850.

[4] KROLL L, BLAU P, WABNER M. Lightweight components for energy-efficient machine tools[J]. CIRP Journal of Manufacturing Science and Technology,2011,4(2):148-160.

[5] LI B, HONG J, LIU Z F. Stiffness design of machine tool structures by a biologically inspired topology optimization method[J]. International Journal of Machine Tools & Manufacture,2014,84:33-44.

[6] ALTINTAS Y. Manufacturing automation[M]. Cambridge, UK: Cambridge University Press, 2000.

[7] QUINTANA G, CIURANA J, TEIXIDOR D. A new analytical-experimental method for the identification of stability lobes in high-speed milling[J]. International Journal of Machine Tools & Manufacture, 2008 ,48:1637-1645.

[8] 杨毅青，刘强，申江丽，等. 基于动力学及切削特性耦合的数控机床结构设计[J].振动与冲击,2013,32(10):198-202.

YANG Yiqing, LIU Qiang, SHEN Jiangli, et al. Machine tool structure design based on the coupling analysis of dynamics and cutting performances[J]. Journal of Vibration and Shock,2013,32 (10):198-202.

[9] WANG J H, LEE K N. Suppression of chatter vibration of a cnc machine center-an example[J]. Mechanical Systems and Signal Processing，1996,10(5):551-560.

[10] ZULAIKA J J, CAMPA F J, LOPEZ L N. An integrated process machine approach for designing productive and lightweight milling machines[J]. International Journal of Machine Tools & Manufacture，2011,51：591-604.

[11] GRAHAM E, MEHRPOUYA M, PARK S S. Robust prediction of chatter stability in milling based on the analytical chatter stability[J]. Journal of Manufacturing Processes,2013,15: 508-517.

[12] IGLESIAS A, MUNOA J, CIURANA J. Optimization of face milling operations with structural chatter using a stability model based process planning technology[J]. International Journal of Advance Manufacture Technology,2014 ,70:559-571.

[13] 刘强,李忠群. 数控铣削加工过程仿真与优化-建模、算法与工程应用[M]. 北京：航空工业出版社，2011.

[14] 汪博，孙伟，闻邦椿. 高速主轴系统切削稳定性预测及影响因素分析[J].机械工程学报,2013,21(49):18-24.

WANG Bo, SUN Wei, WEN Bangchun. Stability prediction and influence factors analysis of high-speed spindle system[J]. Journal of Mechanical Engineering, 2013,21(49):18-24.

[15] LAW M, ALTINTAS Y, SRIKANTHA P A. Rapid evaluation and optimization of machine tools with position-dependent stability[J]. International Journal of Machine Tools & Manufacture，2013,68:81-90.

Analysis and optimization of parameters of machine tool in structure design based on the cutting dynamics with uncertainty

HUANG Hua1, ZHANG Shuyou2, HE Zaixing2, QIU Lemiao2

(1. School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China)

A method for machine tool design parameters optimization was presented to obtain a desirable cutting depth in the milling process, under the constraints of cutting stability and its uncertainty, which have been rarely considered in the traditional design. According to the chatter frequency distribution and the modal tests results, the key influential component of the machine tool which determines the minimal cutting depth was located. Targeting at the thickness of external contour and internal rib of the component, the sensitive design parameters to be modified were selected according to a sensitivity analysis. The difference between the desirable cutting depth and actual cutting depth was converted to an amount for structural dynamic flexibility modification. With the minimum local structural modification, the desirable cutting depth was obtained to meet the requirement of material removal rate (MRR) under the constraint of keeping unchanged the static stiffness and the static weight. The method was verified via the optimization design of a CNC machining center.

cutting dynamics; uncertainty; dynamic compliance; critical limit cutting depth

国家自然科学基金项目(51565030;51275458);甘肃省高等学校科研项目(2015B-032);国家科技重大专项课题(2015ZX04010-011)

2015-02-05修改稿收到日期：2015-05-26

黄华 男，博士，副教授，1978年生

TG502.12; TP391.72

A DOI:10.13465/j.cnki.jvs.2016.14.014