刚柔复合梁压电风能采集器的试验测试与分析

2016-10-18王淑云沈亚林阚君武张忠华严梦加方江海

振动与冲击 2016年18期

关键词：采集器风能压电

王淑云, 沈亚林, 阚君武, 汪　彬, 张忠华, 严梦加, 方江海

(浙江师范大学精密机械研究所，浙江金华　321004)

刚柔复合梁压电风能采集器的试验测试与分析

王淑云, 沈亚林, 阚君武, 汪彬, 张忠华, 严梦加, 方江海

(浙江师范大学精密机械研究所，浙江金华321004)

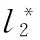
压电；采集器；风能；刚柔复合梁

为满足微功率电子产品及微小型远程传感监测系统的自供电需求、避免大量废弃电池污染环境，电磁、静电、热电及压电式微小型能量采集器(亦称俘能器)的研究已成为国内外的热点[1-3]。每类俘能器都有其自身的优势和适用领域，压电俘能器因具有结构简单、无电磁干扰、易于制作且易于实现结构上的微小化与集成化等优势，适用范围更广。目前，压电俘能器可有效回收人体运动能[4]、环境振动能[5]、旋转体动能[6]以及水流/风能[7]等。前两类压电俘能器研究较早且所获成果较多，已逐步用于无线传感器及健康监测系统等领域。然而，旋转体及流体激励式压电俘能器的研究国内外还都刚开始，尚处于探索和起步阶段。

根据激励方式，现有压电流体俘能器包括风车式[8]、谐振腔式[9]、钝体扰流式[10]及直激式[11-12]四类。前三类的结构复杂、体积相对较大，适用于流体速度较高的场合；直激式俘能器因利用流体流经压电振子时所引起的涡激振动发电，故结构简单、体积小。虽然钝体扰流式及直激式俘能器都是涡激振动发电，但其结构及原理不同：钝体扰流式俘能器利用流体流过圆柱等刚性钝体所形成的漩涡激励压电振子，压电振子长度方向与流体流向相同；而直激式俘能器中，压电振子与流体流向间成一定的夹角，通过流体流过时漩涡的生成与脱落引起的流体压力变化实现自激的。现有直激式俘能器由单一压电振子构成，刚度较大，低流速时不易被激励、高流速时易损毁，应用上有较大的局限性。

为提高低风速时的发电能力，本文提出一种刚柔复合梁压电风能采集器，并进行了理论分析及试验研究，获得了柔性梁尺寸、迎风角及风速对发电性能的影响规律。

1　复合梁压电风能采集器结构及工作原理

刚柔复合梁风能采集器的结构见图1，其中刚度较大的压电梁与其端部串联的柔性梁构成复合梁，复合梁与来风方向的夹角α为迎风角。由流体力学理论，风吹过复合梁时其后方便会产生漩涡，漩涡交替地生成与脱落将使复合梁承受周期变化流体力[13]，从而产生往复弯曲变形并将机械能转换成电能。漩涡脱落频率等于梁的固有频率时将发生共振，发电能力达到最大。

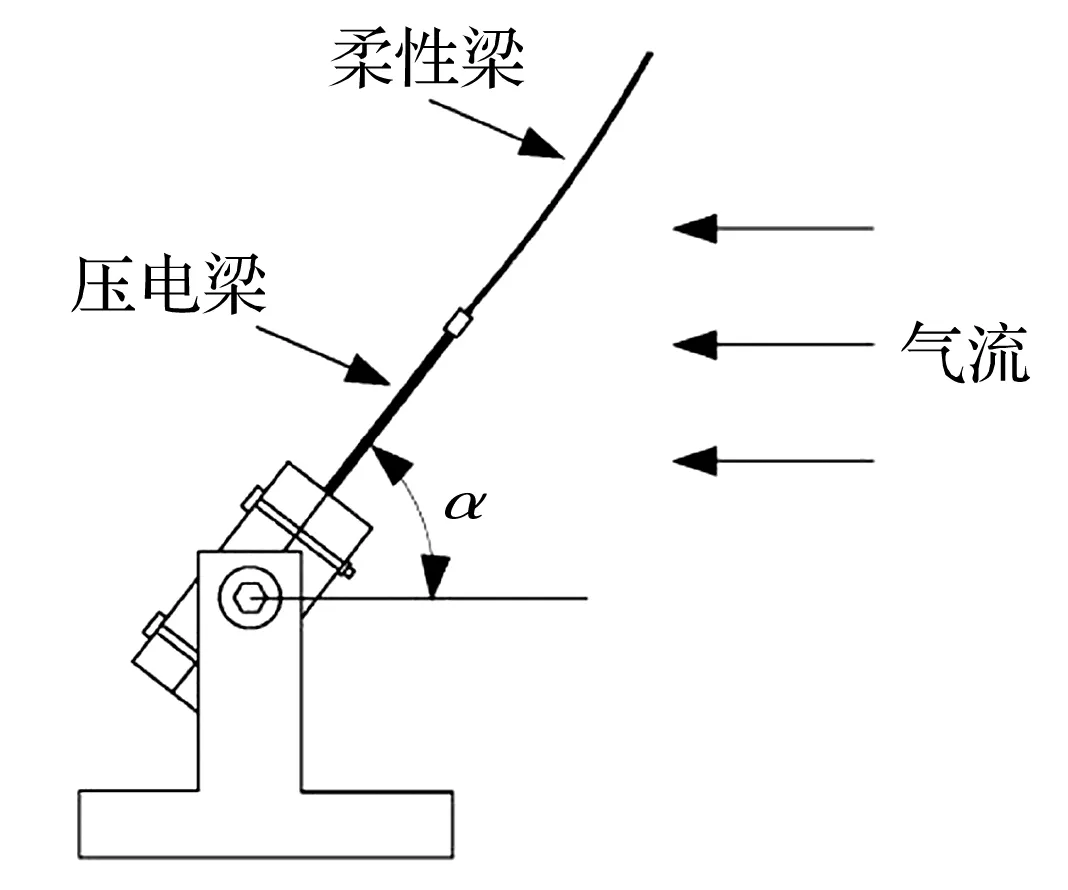
图1　压电风能采集器结构原理图Fig.1　Schematic diagram of piezoelectric harvester

与单一压电梁直吹式风能采集器不同，图1中柔性梁刚度远低于压电梁刚度，低风速时亦可被有效激励，带动压电梁振动发电；高风速时柔性梁变形大，从而减小复合梁的受力面积、避免压电梁因变形量过大而损毁，故可靠性高。

2　复合梁压电风能采集器的理论模型

根据流体力学知识，工作中复合梁所受气体压强及涡激频率可分别表示为：

(1)

(2)

式中：v、ρ分别为风速和气体密度;l1、l2分别为压电梁和柔性梁长度;St为Strouhal数;μL为与雷诺数及结构尺度相关的风力系数。根据振动分析理论，复合梁动力学方程及稳态响应振幅分别为:[14]

(3)

(4)

式中：F0=w(l1+l2)P为复合梁所受的气动激振力;m、c、k分别为复合梁的等效质量、等效阻尼系数及等效刚度;ξ为阻尼比。

以往的研究表明，悬臂型压电俘能器的输出电压与其自由端变形量成正比，所生成的开路电压Vg、单次形变产生的电能Eg及输出功率Pg可分别表示为：

(5)

(6)

(7)

式中：η为与压电梁结构尺寸及材料性能参数相关的系数;Cf为压电陶瓷的电容;R为负载电阻。当R=1/(ωCf)时，输出功率达到最大值，即

(8)

上述公式表明，其它条件确定时可通过改变柔性梁尺度及迎风角调整风能捕获器的输出性能。因电能及输出功率均为开路电压的函数，故本文主要通过试验的方法研究相关参数对输出电压的影响规律。

3　试验测试与分析

图2　压电风能采集器结构及测试系统Fig.2　Piezoelectric energy harvester and test system

为获得风能采集器输出性能与相关参数的关系，设计制作了样机及测试系统(见图2)。所用仪器设备有：风机(额定转速2 850 r/min)、变频器(0～50 Hz，步长0.5 Hz)、DS5042M型示波器及风速仪。压电梁尺寸为45 mm×40 mm×0.5 mm、电容为90 nF、刚度为400 N/m；柔性梁宽度为20 mm、厚度为0.1 mm/0.2 mm/0.3 mm、长度为0～180 mm。试验中能量捕获器置于距风机出口38 mm处，此时垂直面内距离管道中心200 mm范围内的风速基本相同，且与变频器频率f0间呈较好的线性关系(v=0.189f0)。

图3　柔性梁长度不同时输出电压与风速的关系Fig.3　Generated voltage vs wind velocity under different length of flexible beams

图4　柔性梁厚度不同时输出电压与柔性梁长度关系Fig.4　Generated voltage vs length of the flexible beam under different thickness of flexible beams

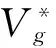
图5　迎风角不同时输出电压与风速关系Fig.5　Generated voltage vs wind velocity under different attack angles

图6　柔性梁厚度不同时输出电压与迎风角的关系Fig.6　Generated voltage vs attack angle under differentthickness of flexible beams

图7　柔性梁长度不同时的电压波形Fig.7　Voltage waveforms generated at different length of flexible beams

图7为v=7.6 m/s、α=40°、h2=0.1 mm、不同l2时的电压波形。对比图中电压波形可发现，随l2增加，振动频率逐渐减小(单位时间内电压波形数，图7(b)和图7(c)的波形数分别为30和25)、电压幅值先增加后减小，这再次说明存在最佳柔性梁长度使输出电压最高；此外，当柔性梁长度处于较佳范围(30～45 mm)时，电压波形较规则且出现了拍振。根据振动分析理论可知，受简谐激励的结构在激励频率ωs接近但不等于其固有频率ωn时有可能出现拍振，且拍频为fp=(ωn-ωs)/(2π)[14]。图7中所显示的频率(如图7(b)中的1.738 Hz)应为拍频而非梁的振动频率。由于拍振的随机性和偶然性以及柔性梁响应的不稳定性，相同试验条件下的电压波形幅值并不稳定。对此，试验中采用增加采样时间(数倍周期)的方法确保记录的均为最大电压值。

以上给出的是相关参数对输出电压的影响规律，根据电压还可获得输出功率(式(7)及式(8))。首先根据式(2)及图7(b)和图7(c)中的波形数，可求得l2=30 mm/45 mm时的激励频率与风速的关系为ωs=24.8v/20.6v，再利用图3中的电压值即可求得相应的功率曲线。鉴于能量采集器振动时出现的拍振使部分电压波形幅值降低，计算时所用电压为实测值的50%。图8和图9分别给出了最佳负载(R=1/(ωCf))时的Pg-v曲线和v=9.5 m/s时的Pg-R曲线。图中曲线表明，输出功率随风速增加呈近似指数关系递增，且l2=45 mm的增幅较大；此外，最佳负载也与柔性梁的长度有关，l2=30 mm/45 mm的最佳负载/功率分别为47.5 kΩ/2.3 mW和 57.5 kΩ/3.6 mW。

图8　最佳负载时功率与风速间的关系曲线Fig.8　Output power vs wind speed under optimal load

图9　风速为9.5 m/s时功率与负载间的关系曲线Fig.9　Output power vs load resistance under v=9.5 m/s

4　结　论

提出一种刚柔复合梁压电风能采集器，并进行了理论分析与试验研究，获得了柔性梁长度l2/厚度h2、迎风角α及风速v对输出电压Vg的影响规律，证明通过选取合适l2/h2/α提高发电能力的可行性，具体结论如下：

(3) 柔性梁长度对复合梁振动频率及振动稳定性有较大影响，振动频率随柔性梁长度增加而减小，柔性梁长度处于较佳范围(30～45 mm)时，输出电压波形较规则，且出现拍振。

[1] BEEBY S P, ZHU D. Vibration energy harvesting: fabrication, miniaturisation and application [J]. Proc of SPIE, 2015, 9517: 951703.

[2] MATIKO J W , GRABHAM N J , BEEBY S P， et al. Review of the application of energy harvesting in buildings [J]. Meas Sci Technol, 2014, 25: 012002.

[3] NIELL E, ALPER E. Advances in energy harvesting methods [M]. New York: Springer-Verlag New York Inc., 2013.

[4] DELNAVAZ A, VOIX J. Flexible piezoelectric energy harvesting from jaw movements [J]. Smart Mater Struct, 2014, 23:105020.

[5] DAQAQ M F, MASANA R, ERTURK A, et al. On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion [J]. ASME Appl Mech Rev, 2014, 66(4): 040801.

[6] 阚君武,于丽,王淑云,等.一种旋磁激励式圆形压电振子发电机 [J].振动与冲击, 2015, 34(2): 116-120.

KAN Junwu, YU Li, WANG Shuyun, et al. A piezodisc energy generator excited by rotary magnets [J]. Journal of Vibration and Shock, 2015, 34(2): 116-120.

[7] TRUITT A, MAHMOODI S N. A review on active wind energy harvesting designs[J]. International Journal of Precision Engineering and Manufacturing,2013,4(9):1667-1675.

[8] LUONG H T, GOO N S. Use of a magnetic force exciter to vibrate a piezocomposite generating element in a small-scale windmill [J]. Smart Mater Struct, 2012,21: 025017.

[9] SKOW E, KOONTZ Z, CUNEFARE K, et al. Hydraulic pressure energy harvester enhanced by Helmholtz resonator[C]// Active and Passive Smart Structures and Integrated Systems. San Diego, CA: SPIE 9431,2015.

[10] SIVADAS V, WICKENHEISER A M. A study of several vortex-induced vibration techniques for piezoelectric wind energy harvesting[C]// Active and Passive Smart Structures and Integrated Systems. San Diego, CA: SPIE 7977, 2011.

[11] HOBECK J D, GESLAIN D, INMAN D J. The dual cantilever flutter phenomenon: a novel energy harvesting method[C]// Active and Passive Smart Structures and Integrated Systems. San Diego, CA: SPIE 9061, 2014.

[12] WU N, WANG Q, XIE X D. Wind energy harvesting with a piezoelectric harvester [J]. Smart Mater Struct,2013, 22: 095023.

[13] 罗惕乾. 流体力学 [M]. 北京：机械工业出版社，2007.

[14] SINGIRESU S R. 机械振动[M]. 4版.李欣业，等，译.北京:清华大学出版社, 2013.

Test and analysis of piezoelectric wind energy harvester based on rigid-flexible composite beam

WANG Shuyun, SHEN Yalin, KAN Junwu, WANG Bin,ZHANG Zhonghua, YAN Mengjia, FANG Jianghai

(Institute of Precision Machinery, Zhejiang Normal University, Jinhua 321004, China)

piezoelectric; energy harvester; wind energy; rigid-flexible composite beam

国家自然基金项目(61574128;51277166;51377147;51577173);浙江省自然基金(Y16F010012);国家级大学生创新创业训练计划项目(201410345004;201410345010)

2015-07-17修改稿收到日期：2015-09-23

王淑云女，博士,教授，1965年生

阚君武男，博士,教授,博士生导师，1965年生

E-mail:jutkjw@163.com