基于差分进化算法的应急指挥堵控算法

基于差分进化算法的应急指挥堵控算法

科学合理地调度警力资源处理突发事件是提高公安部门执法能力的重要因素，为了优化调度方案并提高执法信息化水平，建立了以犯罪嫌疑人在逃时间最短的0-1整数规划模型。为了实现快速高效堵控，采用改进的差分进化算法求解最佳堵控方案。

近年来，随着我国改革开放的不断深入和社会经济的迅速发展，公安机关的执法面临更多的挑战。由于警力不足以及管理体制的原因，应急指挥经常呈现反应不及时和处置滞后等弱点。运用现代化的计算工具提高警力合理使用与调度的水平对于进一步提高公安机关的服务水平和实战能力显得尤为重要。

随着城市规模日益扩大，公安机关指挥处理重大突发事件时需要调度警力资源对交通要道进行封锁。相对于整个城市来说，警力资源肯定是不足的，处理突发事件时需要将平时分散部署的警力资源调度到某些位置实现“堵控”，这是一个受到资源不足约束的调度问题。如何构建合理的模型并利用快速有效的算法求解警力的调度与指挥方案，对公安机关提高处理应急事件的能力具有重要的意义。

本文为研究犯罪嫌疑人的堵控问题，建立以犯罪嫌疑人在逃时间最短为目标的堵控模型，设计基于差分进化算法的全市警力资源调度的算法求解该问题。

模型建立

设某城市有n 个路口｛P1， P2，…Pn｝及m 个警力资源｛S1， S2…，Sm｝，在t0时刻接到报警称在城市Pk，（k=1，2，…，n）路口发生了重大刑事案件，犯罪嫌疑人乘坐交通工具正在逃跑，为了堵控犯罪嫌疑人，需要搜索堵控路口集合｛P1， P2，…Pq｝以及相应警力资源｛S1， S2…，Sq｝的调度方案，确保将犯罪嫌疑人有效“围住”。该问题的最优方案需要满足警力资源｛S1， S2…，Sq｝能在最短时间从原先部署位置调度到堵控路口集合｛P， P…P｝，且

12q犯罪嫌疑人没有逃出堵控路口集合所形成的包围圈。

假设各路口交通畅通，案发地点和警力资源的位置在路口节点，每个路口只需要一个警车的警力即可封锁，罪犯逃跑方向是远离案发地点，罪犯的逃跑速度仅为60km/h。设xij为0-1变量，xij=1表示从第i 个路口的警力资源向第j个路口节点处调度，xij=0表示不从第i 个路口的警力资源向第j个路口节点处调度。xij是决策变量，也是问题的解。问题的最优方案应该满足三个要求：（1）犯罪嫌疑人最大堵控时间最小化；（2）警力资源由外向内调度；（3）犯罪嫌疑人到达某路口的时间大于或等于警力资源到达该路口的时间。

（1）堵控方案的最主要目标就是警力资源最短时间内控制犯罪嫌疑人的逃窜，使其可能的在逃时间最小，即警力资源到达所有堵控节点所用时间的最大值最小化，由此建立目标函数：

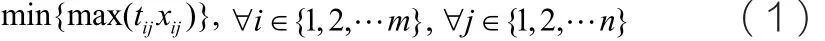
其中，tij表示第i 个警力资源到达第j个路口节点的最短时间，max（tijxij）表示调度方案中警力部署到指定路口节点的最长时间。

（2）考虑到追捕嫌疑人的策略，警力资源从外向内调度，建立约束条件如下：

（3）为保证第i 个警力资源调度到第j个路口围住犯罪嫌疑人，则警力资源一定要在犯罪嫌疑人之前到达第j个路口节点，所以警力资源从第i 个到第j个路口所用调度时间一定要小于等于犯罪嫌疑人到达第j个路口节点的时间，建立约束条件如下：

综上所述，堵控问题的数学模型可以表示为：

算法设计

该模型是一个0-1非线性规划问题，求解此类问题的传统方法有共轭梯度法、变尺度法、分支定界法、广义Benders分解法、外近似法等。由于上述传统方法计算量随着变量维数的增加而急剧增大，一般不能用于实时控制，难以满足本文提出的问题的要求。近年来，随着人工智能技术的提高，各种智能优化算法如遗传算法、粒子群优化算法、蚁群算法以及差分进化算法在不同领域得到了广泛的应用。差分进化算法（DE）是Storn等人于1995年共同提出的一种采用浮点矢量编码，和其它演化算法一样，是一种模拟生物进化的随机模型，在连续空间中进行启发式随机搜索的优化算法，具有较强的全局收敛能力和鲁棒性。

差分进化算法采用浮点数编码，要将其用于求解0-1非线性整数规划问题，必须先对其进行改进，主要是编码转为0-1整数。由于DE的基本操作包括变异、交叉，选择是根据适应值大小进行，这与其他进化算法是类似的。改进主要是进行初始化时对0-1变量先在｛0，1｝实数空间取值，然后根据其特点对变异操作进行改进，即采用四舍五入法进行取整运算，得到对应的0-1变量，就可以将DE用于0-1非线性规划问题。

变量描述与初始化

DE种群的每个个体是调度优化问题的一个解决方案，由n 个决策变量组成，用矩阵表示（k=1，2，…，n ，其中t 表示第t 代）：

其中，xij为0-1变量，表示从第i个路口的警力资源向第j个路口节点处调度。

按照式子（7）对决策变量X 初始化，其中，XL和XU分别为下限和上限，r为在［0，1］上服从均匀分布的随机数。首先在｛0，1｝实数空间随机取值，然后四舍五入取整，得到0-1整数变量：

变异操作

DE算法中，变异个体是由种群内个体的差分向量经过缩放之后与种群内其他相异个体相加得到的。根据变异个体的生成方法不同，对应就有多种不同的差分进化策略。本文对0-1变量进行变异操作并采用四舍五入的方法进行取整的方程为：

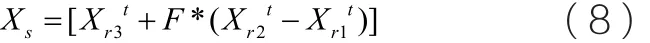
其中，r1≠r2≠r3≠s 为互不相同的随机个体，缩放因子F∈［0，2］。

交叉操作

DE的交叉操作可以保持种群的多样性，进而保持多个可能全局最优的个体，提高搜索的广度。DE算法包括二项式交叉和指数交叉两种交叉方式。本文采用指数交叉。

试验个体XT由群体中第t 代第k 个个体与变异个体Xs进行交叉操作，可以看成是个体的进化。首先通过随机选择使得试验个体XT至少有一位由变异个体Xs提供，其他位可以根据交叉概率因子CR 决定由Xs还是提供。交叉操作的方程为：

若CRmin和CRmax分别为最小交叉概率和最大交叉概率，Tmax为最大迭代次数，则CR 由下面式子确定：

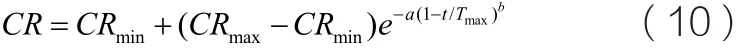
其中参数a=30，b=3

图1　算法流程图

选择操作

DE采用“贪婪”选择策略，将变异和交叉操作后生成的试验个体XT与Xkt进行竞争，根据适应度值f（·）来选择最优个体，若试验个体XT适应度值比Xkt更优时，则将其选为子代，否则将Xkt选为子代。选择操作的方程为：

约束条件处理

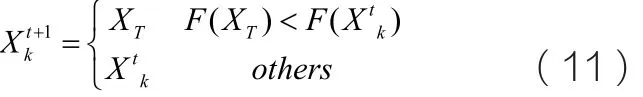
由于约束条件通常都是非线性的，一般采用惩罚函数法将带约束条件的原问题转为无约束问题。经过惩罚函数转化后的无约束问题可定义为：

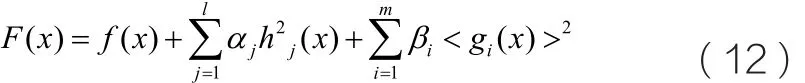
其中αj和βi为大于零的惩罚因子。

算法流程

算法流程如图1所示。

仿真实验

系统环境

硬件CPU频率2.4GHz，内存16GB，操作系统Centos7.0，仿真软件平台Matlab2015。

实验数据及参数设置

以2011年大学生数学建模竞赛B题数据为实验数据，根据算法思想编程求解，得到警力资源的堵控方案如下：

结语

本文针对公安机关在处理突发事件时警力调度问题，建立以犯罪嫌疑人在逃时间最短为目标，警力资源由外而内、警力资源先于犯罪嫌疑人到达路口为约束的调度策略的0-1规划模型，并就该模型采用差分进化算法进行求解。仿真实验结果表明，该方法能够快速有效解决警力调度问题，具有一定的实际意义和应用价值。

10.3969/j.issn.1001- 8972.2016.18.012