混合模拟退火与粒子群优化算法的无人艇路径规划*
2016-10-18郑佳春吴建华
郑佳春, 吴建华, 马 勇, 龙 延
(1.集美大学,福建 厦门361021; 2.武汉理工大学,湖北 武汉430063)
混合模拟退火与粒子群优化算法的无人艇路径规划*
郑佳春1, 吴建华2, 马勇2, 龙延1
(1.集美大学,福建 厦门361021; 2.武汉理工大学,湖北 武汉430063)
针对水面无人艇路径规划中单独使用模拟退火算法存在的不足,以提高无人艇在执行任务时的安全性为研究目的,解决传统无人艇在航行中未考虑来往船只而导致的碰撞危险,提出了模拟退火算法与粒子群算法相结合的混合路径规划算法,利用该算法的高收敛性和容易跳出局部最优等特点,结合避碰规则,实现海事无人艇在同一静态环境下对遇、交叉和追越三种会遇局面的最优路径规划。仿真结果表明:本文提出的算法可以实现无人艇在复杂水域条件下快速路径规划,使与他船的自动避碰行为成为可能,给出的路径规划具有可行、有效,能够为无人艇安全的航行、顺利的执行任务提供保障。
混合模拟退火与粒子群算法;无人艇;最优路径规划;自动避碰
引用格式:郑佳春, 吴建华, 马勇, 等. 混合模拟退火与粒子群优化算法的无人艇路径规划[J]. 中国海洋大学学报(自然科学版), 2016, 46(9): 116-122.
ZHENGJia-Chun,WUJian-Hua,MAYong,etal.AHybridoptimizationalgorithmofSimulatedAnnealingandParticleSwarmforUnmannedSurfaceVesselPathPlanning[J].PeriodicalofOceanUniversityofChina, 2016, 46(9): 116-122.
随着海洋资源的探索与开发,无人艇(UnmannedSurfaceVessel,USV)已经成为当前的研究热点[1-5]。路径规划是USV自主导航的关键技术之一,其核心技术是路径规划算法(PathPlanningAlgorithm,PPA)。目前常见的路径规划算法主要有:Dijkstra算法、神经网络算法、禁忌搜索算法、人工势场法、模拟退火算法、蚁群算法、遗传算法、粒子群算法等。在无人艇路径规划领域,庄佳园等[6]利用去噪平滑算法和自适应阈值法设计了一种基于航海雷达图像处理的方法,采用Dijkstra算法搜索最佳路径;陈超和唐坚[7]提出一种将A*算法与可视图法相结合的路径规划算法,解决了传统可视图法灵活性差的问题并通过实验验证了该算法的有效性;饶森[8]将路径规划的基本技术提升至分层次规划运行,其在对分层路径寻优的研发中,对ActivateValue计算方法与遗传算法协同融合,进行了全局路径规划的计算机仿真实验;但是,这些算法均存在局部最优和收敛性问题。粒子群算法(ParticleSwarmOptimization,PSO)是近年来发展起来的进化算法,和模拟退火算法相似,也是从随机解出发,通过迭代寻找最优解,也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,它没有遗传算法的“交叉”和“变异”操作,它通过追随当前搜索到的最优值来寻找全局最优。在PSO中,粒子飞行速度直接影响算法的性能:如果速度太大,微粒可能飞过最优解;反之,微粒容易进入局部搜索空间而导致无法进行全局搜索。为此,本文提出在PSO算法引入模拟退火机制更新粒子的位置和速度,计算更新前后的粒子适应度及其差值,对进化后的适应值按Metropolis准则接受优化解并以一定的概率接受恶化解,使PSO算法能从局部极值区域中跳出,收敛至全局最优粒子群解。利用该混合算法(SAPSO)的高收敛性和容易跳出局部最优等特点,结合避碰规则模拟仿真获取海事无人艇(MarineUnmannedSurfaceVessel,MUSV)自主避障的最优路径规划,取得很好的效果。
1 MUSV海上环境建模
考虑近海水域内,船舶数量多、交通流量大的特点,结合相关海上避碰规则;再综合对比栅格法[9-10]、单元树法[11]、可视图法[12]、Voronoi[13-15]等常用环境建模方法的优缺点,选择采用栅格法二维平面空间按以下步骤进行环境建模:
(1)确定栅格粒度:假设:lmax是栅格的最大边长,lmin是栅格的最小边长,l是最终的栅格边长,Sab为障碍物的面积和,Stotal为地图区域总面积,LM为MUSV在运动中的最大宽度,则栅格粒度大小为:
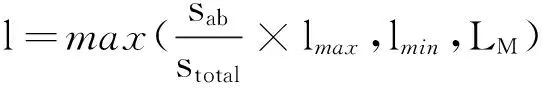
(1)
式(1)中,max表示取最大值。
(2)建立栅格坐标系:以左上角为坐标原点,水平向右横坐标增加为X轴,垂直向下纵坐标增加为Y轴。同时采用序号法和直角坐标法相结合来表示栅格。每个栅格的位置用该栅格的中心点坐标来描述,用(x,y)表示,例如:栅格1的坐标表示为(0.5,0.5)。
假设:Xmax表示X轴坐标的最大值,Ymax表示Y轴坐标的最大值,NX,NY分别表示X轴、Y轴的最大栅格数,由式(1)可得:NX=Xmax/l,NY=Ymax/l。
栅格用序号的表示以左上角为坐标的原点,水平向右,自上到下依次对每个栅格进行编号,编号的顺序为1,2,3,…。栅格位置坐标(x,y)与栅格编号i的映射变换关系如式(2)、(3)、(4)所示。
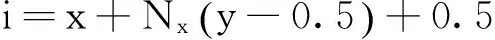
(2)
x=mod((i-1),Nx)+0.5,
(3)
y=fix((i-1)/Nx)+0.5。
(4)
式(3)中,mod表示取余函数,式(4)中fix表示取整函数。
(3)障碍区的栅格处理:忽略MUSV的旋转运动,则障碍物可视为整体障碍区。为了航行安全和避免算法出现局部死区,将障碍区作如下处理:1)如果划分区域内的障碍物不满1个栅格,按1个栅格表示;2)将障碍物内的空凹部分与该障碍物连成1个整体;3)如果2个障碍物间的距离较近,则把这两个障碍物连成为1个障碍物。在二维栅格坐标(x,y)存在障碍物时,B(x,y)采用表示:
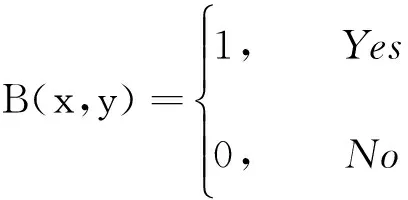
(5)
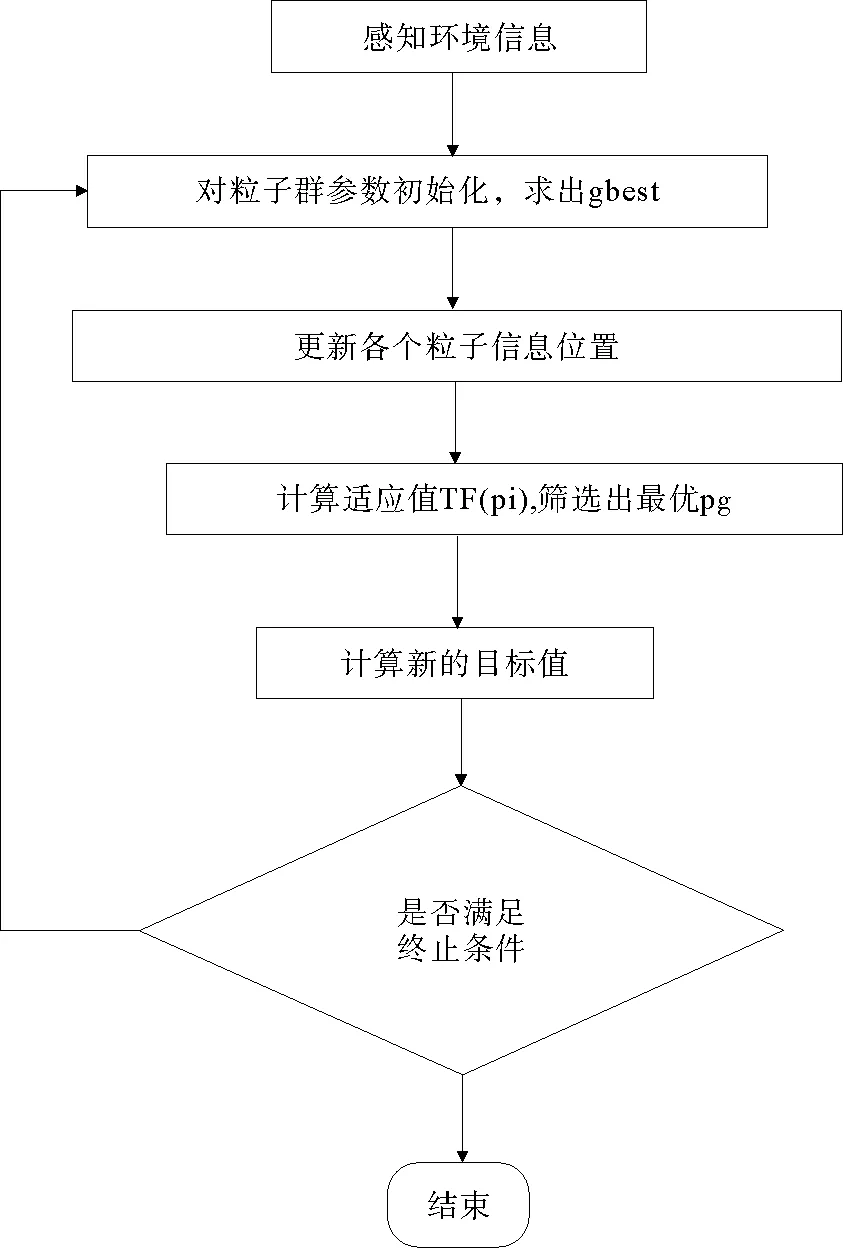
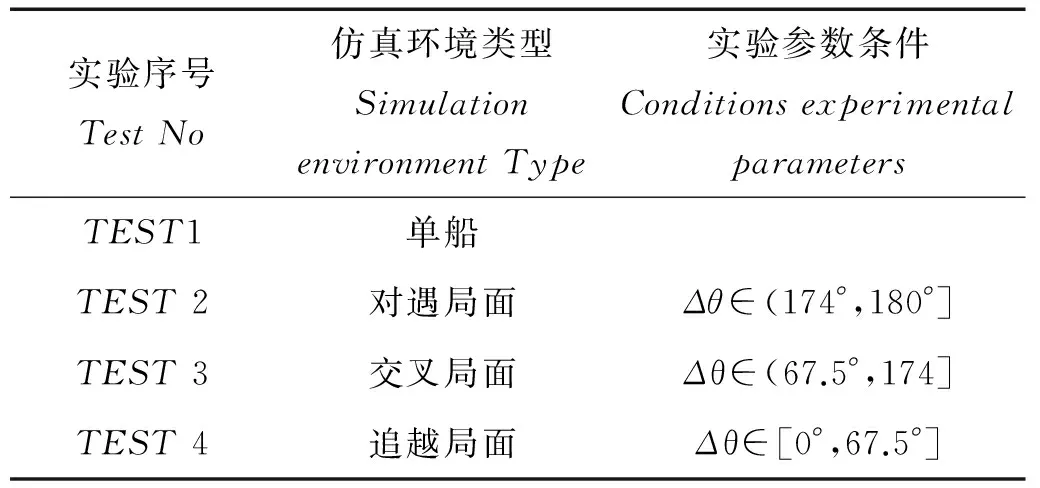
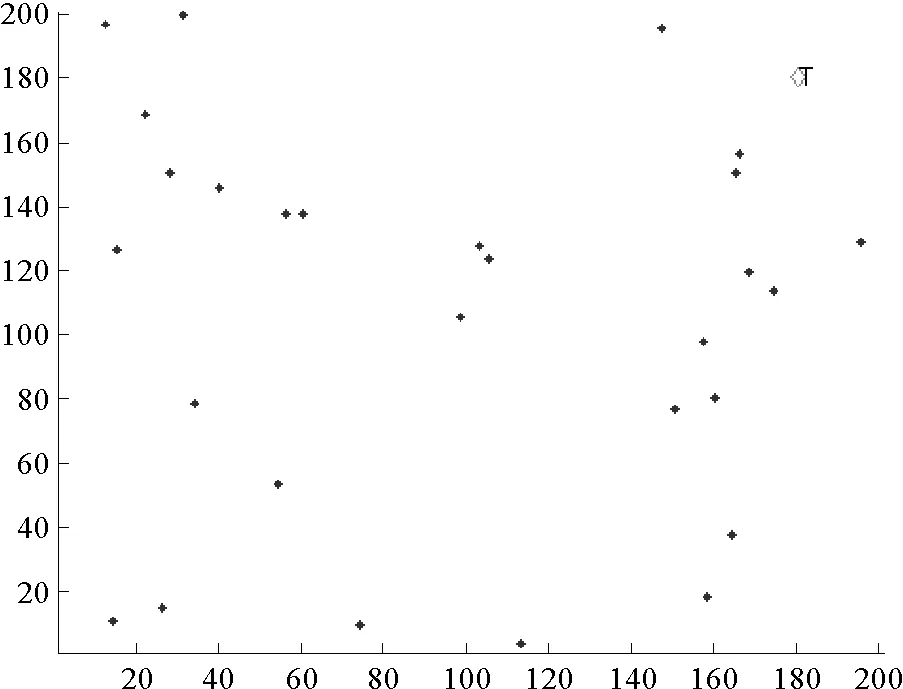
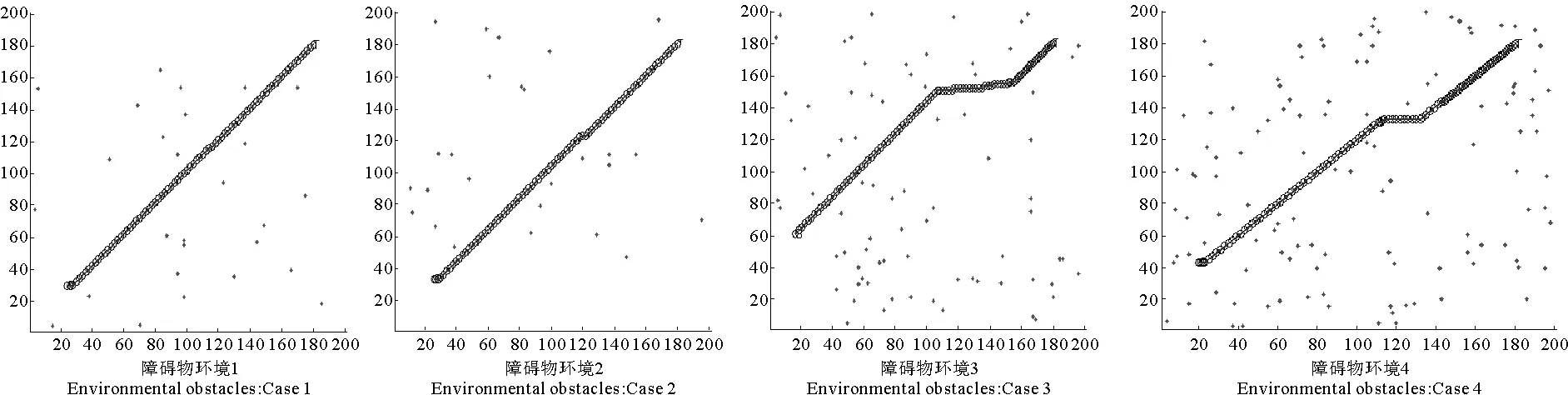
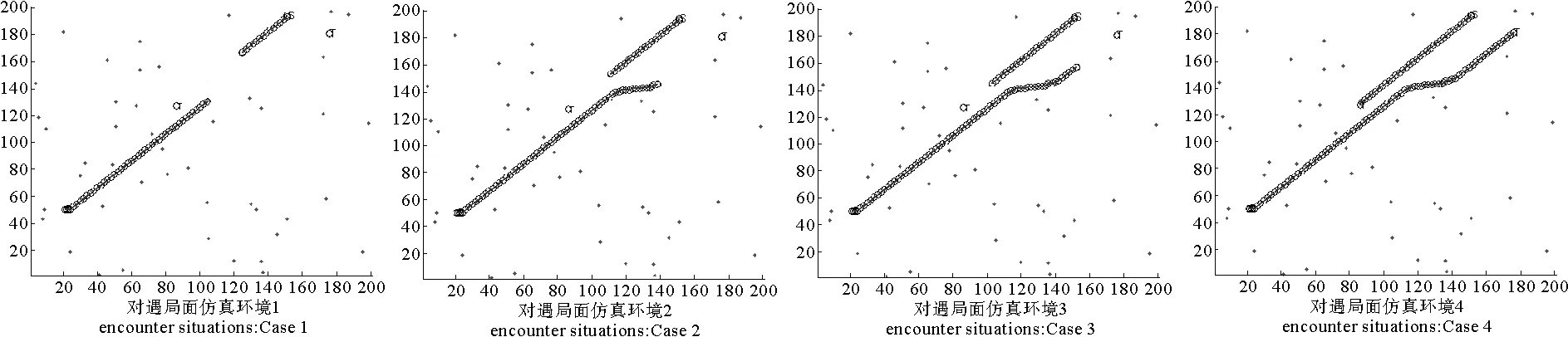
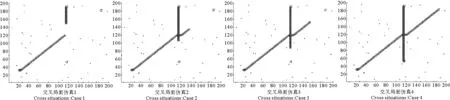
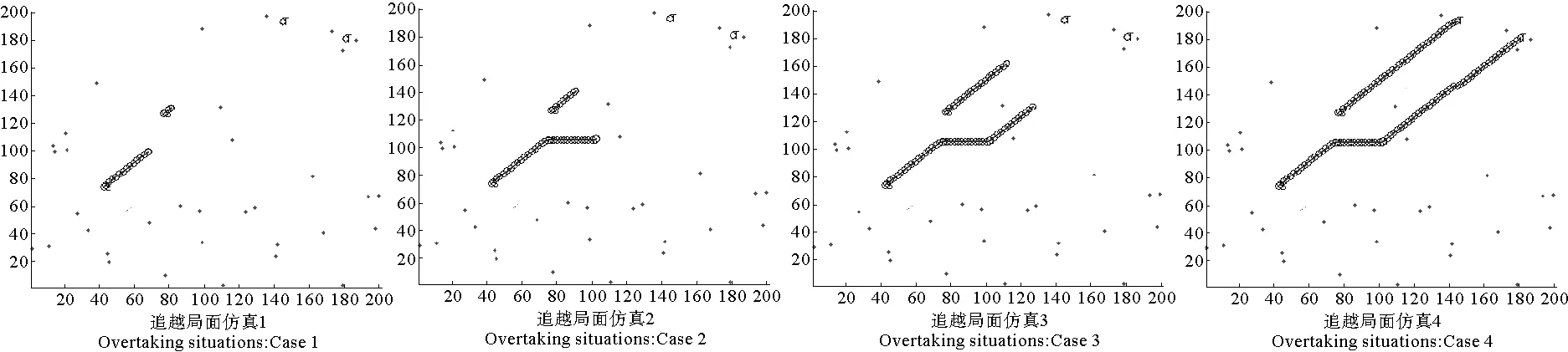
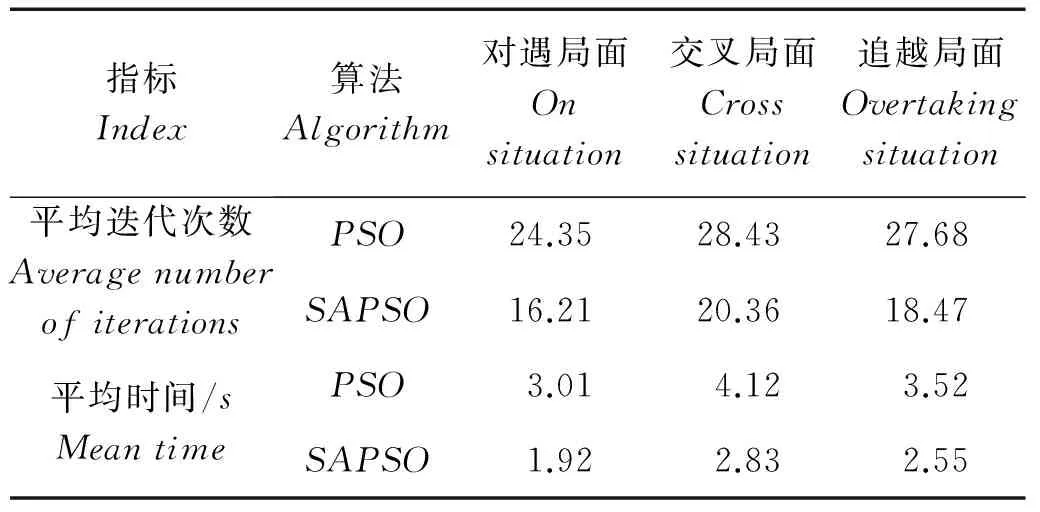
式(5)中,0 (4)环境场景设置为海上静态环境和动态环境。静态环境为已知障碍区的位置和数目,同时,不考虑船舶纵向运动以及外界环境对船舶运动的影响;动态环境为海事无人艇实际航行中,既要按航线的要求行进,还会受到风、浪和流的影响,也需要考虑一些随机因素的影响,如附近船舶的航行,水面漂浮物,以及其他突然出现的干扰等。本文研究时暂不考虑风浪流等因素对MUSV路径规划的作用,动态环境也主要是考虑与他船对遇、交叉、追越的3种局面。 2.1 问题描述 MUSV的路径规划问题可以描述为:某一海事无人艇在假定的条件和参数下,感知外界环境信息,在可航行区域内避开其他船舶的干扰,从设定Start点寻求最短航线L到达设定Target点。路径规划过程如下: (1)设置仿真无人艇的基本参数,包括艇长、艇宽、吃水及控制方程。 (6) 式(6)中,T为追随性指数(s),ω为旋回角速度(1/s),K为旋回性指数(1/s),δ为舵角。 (2)提取电子海图中岛屿、滩涂、航标等障碍物信息,建立栅格坐标系并分别以0、1表示可航区域与不可航区域。提取动态船舶信息并预测其路径趋势,根据与来船的方位差Δθ判断本船责任。 (3)无人艇与障碍物之间的距离(D)要求大于最小安全距离(dmin)。 D≥dmin。 (7) 相对距离(d)代表碰撞危险度如式(8)所示,当d小于设定值时,无人艇转向避让。 (8) (4)选取巡航出发点S(x0,y0)和目标点T(xt,yt)坐标;基于SAPSO求解可行路径的解空间: (9) 式(9)中,L为规划路径的总长,Li为第i段路径的长度。选取出路径最短的解为最优规划路径,得到最优解minL。 2.2 混合模拟退火机制的粒子群算法 SAPSO算法描述如下: (a)随机初始化种群中各个微粒的位置及速度,并按式(10)设置初始温度; t0=f(pg)/ln5。 (10) 式(10)中,pg为种群的群体极值,其选择为粒子群中适应值的最大值。 (b)将当前各个微粒的位置及适应值存于个体极值(pi)中,将适应值最优个体(pbest)的位置及适应值存储于pg中,根据式(11)计算各个微粒的适应值。 (11) (c)从所有pi中确定全局最优适应值更新pg,然后用式(12)更新各个微粒的速度,以式(13)更新各个微粒的位置。 vi,j(t+1)=φ{vi,j(t)+c1r1 (12) xi,j(t+1)=xi,j(t)+vi,j(t+1)·T, j=1,2,…, MaxDT。 (13) (d)计算各个微粒新的目标值,更新各个微粒的pi值及群体的pg值; (e)进行退温操作,退火方式按式(14)进行。若满足终止条件:运算精度或迭代次数达到预定值,搜索停止,输出结果,否则转向步骤(b)。算法流程图如图1所示。 图1 SAPSO算法流程图Fig.1 SAPSO algorithm flow chart tk+1=λtk。 (14) 式(14)中,λ为退火系数。 仿真时,基本参数设定为初始化粒子群体个数n=50,设定最大迭代次数MaxDT=50,搜索空间维数D=8。 3.1 仿真环境 表1 仿真条件 表2 仿真船舶基本参数 注:MUSV数据以国内自主研发的第一艘无人巡航艇为例;它船数据来源于《海港总平面设计规范》(JTJ156-2013)。 Note:MUSVdataisbasedonthefirstunmannedcruiseofindependentresearchanddevelopmentboat;othership'sdataisfromthe《Seaporttotalgraphicdesignspecification》(JTJ156-2013) 3.2 环境栅格模型的建立 3.2.1 静态障碍物坐标系上建立200×200的栅格,所建坐标以m为单位,以左下角为坐标原点O,横坐标、纵坐标每格均代表100m。在栅格环境中随机散布仿真静态障碍物,在MATLAB界面上显示,输出如图2所示,图中圆圈T代表无人艇巡航的目的地。 图2 栅格环境图 3.2.2 动态障碍物MUSV在活动范围内随时可能出现其他活动船舶,因此在MUSV的路径规划中还需解决如何处理与来船会遇局面的避碰问题。MUSV在动态环境中采取主动避让措施,具体方案是:首先判断与动态障碍物(来船)的距离,若d≤200m,再进一步确定与来船航向差,然后根据避碰规则决定采用何种避碰措施,即进行速度避让或航向避让,从而实现主动避碰。 3.3 单船路径仿真 本文首先在无他船干预的情况下进行单船路径仿真,即:根据MUSV仿真参数,在随机障碍物条件下,实现MUSV的日常海事巡航,航线为固定起始点S点到固定目标点T点的路径规划。在200×200的栅格环境中,变换环境中障碍物的数量,如图3所示,MUSV所在水域的障碍物数量不断增加,在同样的位置设置起始点和目标点,输出MUSV路径仿真图。从仿真图中看出,在该算法下,MUSV依然能规划出一条从起始点S到目标点T的一条不碰路径,说明在障碍物数量变化的情形下,实现MUSV的路径规划也是可行的。 图3 单船路径环境仿真 3.4 会遇局面下的路径仿真 会遇局面下的路径仿真包括在目标点之间的安全航行和与他船单船发生对遇、交叉和追越3种局面下的自主避障。 3.4.1 与来船对遇局面仿真在仿真实验下,MUSV与来船航向差范围在(174°,180°]内,当与来船接近至设定距离为200m(当目标船与MUSV间的相对距离小于等于200m时,即认为有碰撞危险,需对危险船采取避让措施),MUSV右转,让清他船后重新规划最短路径直至目标T点。如图5.4~5.6所示,假设他船航向保持不变,由右上起始点S驶往左下方目标T,下方蓝色轨迹线为MUSV航行轨迹,由左下起始点S往右上目标点T行驶,中间的航迹段为MUSV绕过障碍物及让清他船的过程图。 对遇局面下MUSV避让过程为:(1)图4-1,MUSV与他船同时从起始点S出发相向而行,航行一段时间后MUSV与来船之间距离为200m,且航向差范围在(174°,180°]内;(2)图4-2,根据航行规则,他船航向保持不变,MUSV为让路船大幅右转让清他船;(3)图4-3,MUSV在避让成功后,重新规划到目标点T的最短路径;(4)图4-4,MUSV在避开静态障碍物及来船后,完成了从起始点S到目标点T的路径仿真。 图4 对遇局面仿真 通过以上3组仿真实验可以看出,MUSV与来船在对遇局面下,能成功避让静态障碍物及来船,并能在遵守海事无人艇避碰规则前提下,完成起始点S到目标点T的路径规划任务。 3.4.2与来船交叉局面仿真当Δθ∈(67.5°,174°]时,视为交叉局面,MUSV属于机动性强的小艇船舶,与机动性较差的大型船舶会遇时应承担让路责任。他船为位于MUSV右舷时,属于大角度交叉局面,MUSV为让路船,当两船之间直线距离小于等于200m时,MUSV大幅度右转从他船后方驶过让清他船,然后重新规划最短路径。如图5示,为MUSV与他船交叉局面下的航行轨迹,航行轨迹为蓝色轨迹线,由左下起始点S往右上目标点T行驶。 交叉局面下MUSV避让过程为:(1)图5-1,MUSV与他船同时从起始点S出发,为(67.5°,174°]的交叉局面,航行一段时间后,他船为位于MUSV右舷时;(2)图5-2,他船航向航速保持不变,MUSV为让路船与来船之间距离为200m,此时MUSV大幅度右转从他船后方驶过让清他船;(3)图5-3,MUSV在避让成功后,重新规划到目标点T的最短路径;(4)图5-4,MUSV在避开静态障碍物及来船后,完成了从起始点S到目标点T的路径仿真。 图5 交叉局面仿真 通过以上三组仿真实验可以看出,MUSV与来船在交叉局面下,能成功避让静态障碍物及来船,并能在遵守海事无人艇避碰规则前提下,完成起始点S到目标点T的路径规划任务。 3.4.3 追越仿真当Δθ∈[0°,67.5°]时,视为追越局面发生,仿真实验中MUSV追越他船,根据MUSV在避碰规则,追越船舶有让路责任,右转从他船右舷驶过,而被追越船保速保向。MUSV通常速度较快,追越他船的常有发生局面,此时MUSV为让路船,在本次追越过程中右转,超过他船后重新规划最短路径,仿真结果如图6所示,坐标系中MUSV航行轨迹为长轨迹线,他船航行轨迹为短轨迹线,同由左下方往右上方行驶。 追越局面下MUSV避让过程为:(1)图6-1,MUSV与他船同时从左下角起始点S出发,由于MUSV速度快,航行一段时间后MUSV与来船距离缩短,并与被追越船之间距离为200m,且航向差范围在(174°,180°]内;(2)图6-2,根据航行规则,他船航向保持不变,MUSV右转从他船右舷驶过;(3)图6-3,MUSV重新规划后到目标点T的最短路径后,与他船距离远大于200m;(4)图6-4,MUSV在避开静态障碍物及来船后,完成了从起始点S到目标点T的路径仿真。 图6 追越局面仿真 通过以上3组仿真实验可以看出,MUSV与来船在追越局面下,能成功避让静态障碍物及来船,并能在遵守海事无人艇避碰规则前提下(MUSV从他船右舷驶过),完成起始点S到目标点T的路径规划任务。 3.5 仿真结果分析 设置同样的起始点S和目标点T,对三种会遇局面(对遇、交叉、追越)分别进行20次反复实验,得出如表3所示的统计数据。 通过分析上述USV的仿真实验结果,可以得出以下几个结论: (1)SAPSO算法迭代中只涉及初等运算,运算量少,速度快; (2)起始点和目标点之间的距离越远、障碍物越多,MUSV规划所需时间较长; (3)SAPSO算法运算收敛于最优解的几率高,能完成起始点到目标点的路径规划任务; (4)系统通过判断MUSV与静态障碍物是否有碰撞危险采取避碰决策,能根据静态障碍物的分布位置规划出最短路径。 (5)在更为复杂的动态障碍物环境中,MUSV能根据与他船的会遇态势做出符合避碰规则的规划,自身作为让路船调整航向实现避碰。 表3 仿真数据统计分析 本文采用SAPSO求解MUSV最优路径的问题,取得了较好的效果。通过在同一环境中将他船的行动融入到动态环境模型中,实现了在对遇、交叉和追越三种局面下,MUSV从起点到达目标点自动实施安全避碰决策的仿真实验。仿真结果验证了本文提出的算法可为实现MUSV在执行任务中与其他船舶发生对遇、交叉、追越局面下的自主避障,也可在更为复杂的动态障碍物环境中根据与他船的会遇态势做出符合避碰规则的规划,自动让路调整航向实现避碰。 [1]ShowalterS,ManleyJ.Legalandengineeringchallengestowidespreadadoptionofunmannedmaritimevehicles[C]//ProceedingsofOCEANS2009,MTS/IEEEBiloxi-MarineTechnologyforOurFuture:GlobalandLocalChallenges.IEEE, 2009: 1-5. [2]吴博, 文元桥, 肖长诗. 一种内河海事无人艇路径规划算法设计与仿真[J]. 计算机工程与应用, 2013, 49(14): 241-246. WuBo,WenYuanqiao,XiaoChangShi.Aninlandrivermaritimeunmannedvehiclepathplanningalgorithmdesignandsimulation[J].ComputerEngineeringandApplication, 2013, 49(14): 241-246. [3]王雨迪. 基于自抗扰控制算法的水面无人艇航向自动舵设计[D]. 大连: 大连海事大学, 2014. WangYudi.DesignofCourseAutopilotofUnmannedSurfaceVesselBasedontheImmunityControlAlgorithm[D].Dalian:DalianMaritimeUniversity, 2014. [4]杨炜帆. 水面无人艇的建模与运动特性仿真[D]. 大连: 大连海事大学, 2013. YangWeifan.UnmannedSurfaceVehicleModelingandMtionSimulation[D].Dalian:DalianMaritimeUniversity, 2013. [5]董早鹏. 无人艇运动模糊控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. DongZaopeng.TheResearchofFuzzyControlTechnologyofUnmannedSurfaceVessel[D].Harbin:HarbinEngineeringUniversity, 2013. [6]庄佳园, 苏玉民, 廖煜雷, 等. 基于航海雷达的水面无人艇局部路径规划[J]. 上海交通大学学报, 2012, 46(9): 1371-1375. ZhuangJiayuan,SuYumin,LiaoYulei,etal.ThelocalpathplanningofunmannedsurfacevesselbasedontheMarineradar[J].JournalofShanghaiJiaotongUniversity, 2012,46(9): 1371-1375. [7]陈超, 唐坚. 基于可视图法的水面无人艇路径规划设计[J]. 中国造船, 2013, 54(1): 129- 135. ChenChao,TangJian.Thepathplanningdesignforunmannedsurfacevesselbasedonthemethodofvisibilitygraph[J].JournalofChinaShipbuilding, 2013, 54(1): 129-135. [8]饶森. 水面无人艇的全局路径规划技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2007. RaoSen.ResearchoftheGlobalPathPlanningforUnmannedSurfaceVessel[D].Harbin:HarbinEngineeringUniversity, 2007. [9]王娟娟, 曹凯. 基于栅格法的机器人路径规划[J]. 农业装备与车辆工程, 2009, 47(4):14-17. WangJuanjuan,CaoKai.TheRobotpathplanningbasedonthegridmethod[J].JournalofAgriculturalEquipmentandVehicleEngineering, 2009, 47(4): 14-17. [10]朱庆保, 张玉兰. 基于栅格法的机器人路径规划蚁群算法[J]. 机器人, 2005(2): 132-136. ZhuQingbao,ZhangYulan.Therobotpathplanningofantcolonyalgorithmbasedongridmethod[J].Robot, 2005(2): 132-136. [11]于红斌, 李孝安. 基于栅格法的机器人快速路径规划[J]. 微电子学与计算机, 2005(6): 98-100. YuHongbin,LiXiaoan.Robotfastpathplanningbasedonthegridmethod[J].JournalofMicroelectronicsandComputer, 2005(6): 98-100. [12]Lozano-PerezT,WesleyM.Analgorithmforplanningcollision-freepathsamongpolyhedralobstacles[J].CommunicationsoftheACM, 1979(5): 436-450. [13]刘金义, 刘爽.Voronoi图应用综述[J]. 工程图学学报, 2004(2): 125-132. LiuJinyi,LiuShuang.Voronoidiagramapplicationreview[J].JournalofEngineeringGraphics, 2004(2): 125-132. [14]赵永利. 基于Voronoi图的机器人局部路径规划[D]. 南京: 南京理工大学, 2006. ZhaoYongli.RobotLocalPathPlanningBasedonVoronoiDiagram[D].Working:WorkingUniversityofScienceandTechnology, 2006. [15]卢艳爽. 水面无人艇路径规划算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. LuYanshuang.ResearchonthePathPlanningAlgorithmforUnmannedSurfaceVessel[D].Harbin:HarbinEngineeringUniversity, 2010. 责任编辑陈呈超 A Hybrid Optimization Algorithm of Simulated Annealing andParticleSwarmforUnmannedSurfaceVesselPathPlanning ZHENGJia-Chun1,WUJian-Hua2,MAYong2,LONGYan1 (1.JimeiUniversity,Xiamen361021,China; 2.WuhanUniversityofTechnology,Wuhan430063,China) Withtheexplorationanddevelopmentofmarineresources,UnmannedSurfaceVessel(USV)hasbecomeahotresearchtopic.PathplanningisoneofthekeytechnologiesofUSVautonomousnavigation,anditscoretechnologyisPlanningAlgorithmPath(PPA).Thispaperanalysesandstudiesseveralcommonpathplanningalgorithms,discussestheiradvantagesanddisadvantages.TheParticleSwarmOptimization(PSO)algorithmandSimulatedAnnealing(SA)algorithmareourmainresearchobject,anditisinsufficientbyusingthePSOalgorithmorSAalgorithmalonefortheexistenceofunmannedsurfacevehiclepathplanning.InordertoimprovethesafetyofUSVsailing,tosolvethetraditionalunmannedboatwithoutconsideringthecollisiondangercausedbythecomingandgoingvesselsduringthevoyage,thehybridpathplanningalgorithm(HybridofSimulatedAnnealingandParticleSwarmOptimizationAlgorithm,HSAPSO)combiningSAalgorithmandPSOalgorithmisproposed.TheSAPSOusingthealgorithmcharacteristicsofconvergenceandeasytojumpoutoflocaloptimum,combinedwiththecollisionregulations,itcanbeeasyimplementationtheoptimalpathplanningofUSVinthethreeencountersituationsofheadon,crossingandovertaking,especialforMarineUnmannedSurfaceVessel(MUSV).ThesimulationresultsshowthattheSAPSOalgorithmproposedinthispaperenabletheMUSVtodoautomaticcollisionavoidancebehaviorincomplexwaterconditions,andthegivenpathplanningisfeasibleandeffective.WhichcanprovidesafeguardfortheMUSV’ssafenavigationandsuccessfulimplementationofthetask. hybridofsimulatedannealingandparticleswarmoptimizationalgorithm;marineunmannedsurfacevessel;optimalpathplanning;collisionavoidance 国家自然科学基金项目(51309186)“复杂海况下的海事无人艇路径规划研究”;福建省科技计划重点项目(2014H0036);福建省自然科学基金项目(2013J01203)资助 2015-09-29; 2016-01-20 郑佳春(1965-),男,副教授。E-mail:zheng_xxgc@163.com S948;S943 A 1672-5174(2016)09-116-07 10.16441/j.cnki.hdxb.20150340 SupportbytheNationalNaturalScienceFundProjectofChina(51309186) “ComplexSeaConditionofMaritimeUnmannedCraftPathPlanningResearch”,TheKeyProjectofScienceandTechnologyPlanofFujianProvince(2014H0036);FujianProvinceNaturalScienceFundProject(2013J01203)2 路径规划算法
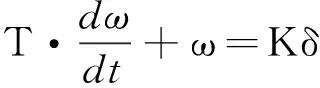
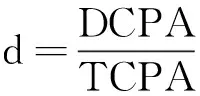
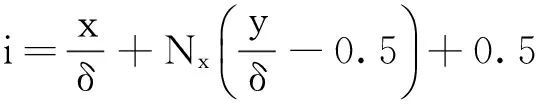
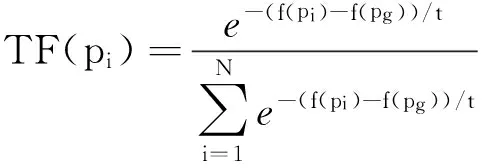
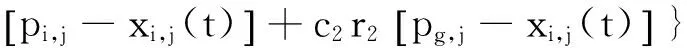
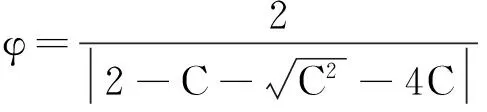
3 SAPSO算法路径规划仿真
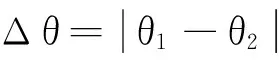

4 结语
