隐身飞机突防建模及低可探测性轨迹规划*

刘鸿福，周文宏，陈少飞

（国防科技大学机电工程与自动化学院，长沙410073）

隐身飞机突防建模及低可探测性轨迹规划*

刘鸿福，周文宏，陈少飞

（国防科技大学机电工程与自动化学院，长沙410073）

针对隐身飞机突防飞行规划，分析了隐身飞机对警戒雷达网突防过程问题特性，建立了雷达探测模型与组网警戒雷达信息融合模型；综合考虑隐身飞机的隐身能力、预警时间和燃料消耗将隐身飞机低可探测性轨迹规划问题形式化为一个复杂多目标非线性连续时间最优控制问题；并提出基于伪谱法的低可探测性轨迹规划方法。仿真实验实现了在组网警戒雷达下隐身飞机的低可探测性突防轨迹规划，证明了方法的可用性和有效性。

警戒雷达网，低可探测性，信息融合模型，伪谱法，轨迹规划

0　引言

技术的发展牵引了作战形式的变迁，随着隐身与反隐身技术的进步，飞行器与防空系统的对抗越来越激烈，单纯依靠隐身技术来实现作战飞机对敌方防空区域突防的可能性已经越来越小。提高隐身飞机突防可能性的一个重要手段就是综合考虑敌方防空区域的地理特征与防空警戒雷达的威胁模型来规划隐身飞机的飞行轨迹，并保证其轨迹对敌方防空警戒雷达具有较低的可探测性。当前航迹规划研究大多集中于航迹优化［1-2］、在线快速规划［3-5］等，较少考虑组网警戒雷达威胁，而雷达威胁是隐身飞机的重要威胁，所以本文对隐身飞机突防警戒雷达网的特性进行了充分的分析，建立了单、双基地雷达对隐身飞机探测的模型，对组网警戒雷达对隐身目标探测的信息融合规则进行建模，随后对隐身飞机低可探测性轨迹规划问题进行了数学形式化，描述为复杂多目标非线性连续时间最优控制问题，研究提出了基于伪谱法的低可探测性轨迹规划方法并进行了仿真实验。

1　分析与建模

1.1隐身飞机对警戒雷达网突防过程分析

警戒雷达的任务是发现和指示目标。组网警戒雷达从多个站点对一个指定的空域实施全方位覆盖探测，对空域内的所有飞行器进行搜索和跟踪，获取监视与警戒信息。布局合理的警戒雷达网可以实现在有限资源的条件下提高整体的目标探测能力。现今的警戒雷达网，一般针对RCS为1m2～5m2的目标具备完全覆盖的探测能力。而已经出现或即将装备的隐身作战飞机，其RCS在0.01m2～0.1m2的范围内，相比较隐身飞机的整体RCS下降了20 dBsm～30 dBsm。但是，隐身飞机的RCS沿其方位角分布复杂，波动剧烈，如图1所示，为隐身无人机在0°仰角估算的RCS曲线［6］。从图1中可看出，原始RCS曲线波动剧烈，有许多高低的尖峰，形如刺猬图，尤其是飞机的侧向RCS值较大，仍具有被探测发现的薄弱方向，特别是针对双基地雷达的探测［7-8］。因此，隐身飞机针对组网警戒雷达的低可探测性突防轨迹需要细致地规划，其过程如图2所示。

图1　X-47B无人机的典型RCS

隐身飞机对组网警戒雷达的隐身轨迹规划与警戒雷达网的工作特性密切相关。其隐身轨迹规划问题特性分析与建模都必须充分考虑中远程警戒雷达、双基地雷达以及雷达网信息融合的实际情况，进而利用其可能的防空漏洞进行隐身规划。从警戒雷达网与飞机的作战目标两方面出发，该规划问题的特性分析如下：

（1）单基地中远程警戒雷达与双基地雷达的波段一般选择为特高频（UHF）波段，以UHF波段（300MHz～1 000 MHz）、L波段（1 GHz～2 GHz）、S波段（2 GHz～4GHz）为主［9］，作战飞机需要重点考虑该波段的隐身，规划建模时需要该波段的飞机RCS模型。

（2）警戒雷达网需要对网内所有雷达探测的信息进行融合，信息融合的处理方式分为集中式与分布式，在中心节点进行集中式处理在较小的目标RCS情况下仍可能检测目标；而分布式融合并未对全局的所有信息进行融合，但提高了雷达网的稳健性与抗摧毁性。信息融合模型是警戒雷达网目标检测模型的重要组成部分。

图2　隐身飞机对组网警戒雷达低可探测性突防示意图

（3）双基地雷达探测隐身飞机的特点与优势。隐身技术使得飞机在鼻翼方向周围区域的后向散射场明显减弱，但同时有可能增强其他方向的散射场，双基地雷达可以利用隐身目标的侧向散射与前向散射增强区［9］。而且，双基地的雷达截面积与单基地的雷达截面积不同，目标相对于双基地雷达探测的RCS与双基地角密切相关，需要对双基地雷达探测进行建模。

（4）警戒雷达网由情报指挥中心直接实施灵活控制，反应速度快，尽可能地实现整个警戒雷达网探测效能最大化。特别是在我方实施电子干扰与反辐射攻击情况下，敌警戒雷达网的探测范围与能力将动态变化［10-11］。因此，有必要按照敌警戒雷达网的惯常工作方式进行建模与规划。

（5）作战飞机对警戒雷达网的隐身规划需要同时兼顾多个优化目标，抵达警戒雷达网的纵深，规避制导雷达及其地空导弹系统威胁之上，尽量压缩敌方的预警时间，同时优化飞行时间、油耗、探测概率等，使得整体的作战效能满意。

1.2隐身目标的双基地雷达截面积模型

双基地的雷达截面积是目标朝接收机方向上所散射能量的度量，对于目标的探测更为有效。双基地的RCS可以由单基地RCS推广得到。除了与单基地RCS类似的特性外，双基地RCS还是收、发基地视线角和双基地角β的函数，可以将双基地RCS作为双基地角β的函数。

双基地RCS比单基地RCS复杂得多。双基地雷达在基线附近存在由直达波所引起的角度盲区以及由杂波随机运动形成的多普勒盲区。模糊区为±（3°～5°），其大小随雷达参数与目标速度相关变化，一般设置模糊区界限为β＞175°；而目标的前向散射增强区为β≥130°，因此，双基地雷达前向散射区大致为130°≤β≤175°。单基地雷达和双基地雷达的数学模型可用文献［12，15］中得到，一般来说，对于形状复杂的目标，通过分析得出了由目标单基地RCS计算双基地RCS的经验公式，将双基地RCS表示为目标的单基地RCS和双基地角的函数［9，13］：

其中，σmon为目标的单基地RCS，β为双基地角，K为经验系数，由目标结构和复杂程度确定［12］，且有：

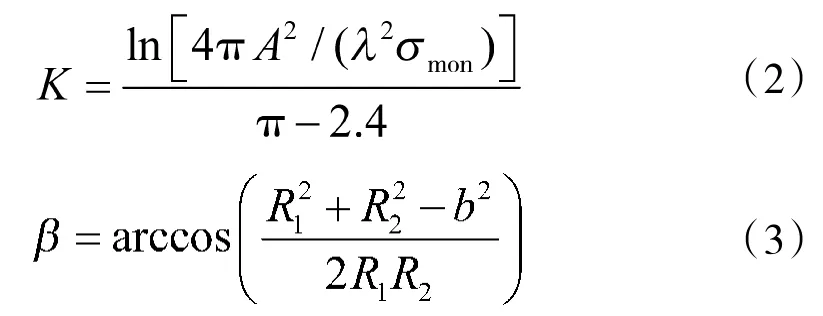
图3　σbi/σmon随双基地角β的变化曲线图

1.3组网警戒雷达信息融合模型

作战飞机在敌方严密的防空体系下突防，不可避免地将受到多部雷达同时探测。多种不同体制雷达组网是反隐身的重要手段，通过组合可显著提高捕获概率。雷达组网的融合探测概率是指信息融合中心得出的来袭目标发现概率［11］。秩K融合规则便于实现，所以在雷达网数据融合中应用非常广泛。本文对警戒雷达网的建模采取秩K规则融合。

假设某雷达网由N部雷达组成，依据秩K融合规则，即当雷达网内发现目标的雷达数超过检测门限K时，判定为发现目标。Schwartz的研究表明［14］，对于在噪声中检测非起伏目标或Swerling起伏目标，当Pf=10-5～10-10且Pd=0.5～0.9时，最优的第二级阈值近似为：

其中N为雷达网中总的雷达数目，例如6部雷达的雷达网，K取4。

图4　秩K融合规则判决流程

秩K融合规则判决流程如图4所示。每部雷达根据对隐身飞机探测得到的信息首先进行局部的判决，即依据设置的检测概率门限值，自己判断是否检测到目标，检测到目标为“1”，否则为“0”。然后将局部判决的结果全部集中到信息融合中心，构成整个的判决空间D。雷达组网信息融合中心采用并行融合结构，融合规则记为R，则判定规则为：

融合后雷达网总的探测概率为：

其中，J0，J1分别为Di中判H0，H1的雷达组合，Pi是第i部雷达的探测概率，D为整个判决空间Di∈D（i=1，2，…，2N）。

同样地，整个雷达网的虚警概率为：

2　隐身飞机低可探测性轨迹规划问题形式化

针对由多部不同体制、频段、极化方式的中远程警戒雷达与双基地雷达组成的警戒雷达网，定义隐身飞机低可探测性轨迹规划问题（Low Observability Trajectory Planning for Stealth Aircraft Against Netted Surveillance Radars，LOTPANA）。设警戒雷达网由Ns台单基地中远程警戒雷达与Nm台双基地雷达组成，相关要素与模型定义如下：

SR：SR=｛SR1，SR2，…，SRNs｝，为单基地中远程警戒雷达的集合；

MR：MR=｛MR1，MR2，…，MRNm｝，为双基地雷达的集合；

NRC：组网雷达信息融合中心，采取秩K规则融合；

R：R=｛RT，RP，RF，SNR，PF，RD｝为雷达的形式化定义，RT为雷达的工作体制，RP为雷达的极化方式，RF为雷达的工作频段，SNR为雷达能够检测的信噪比，PF为雷达的虚警概率，RD为标称的探测距离。

i：雷达索引，i∈｛1，…，Ns+Nm｝；

RCSi（t）：t时刻飞机相对于雷达i的RCS；

Pdi（t）：t时刻飞机被雷达i探测的概率；

PD（t）：t时刻飞机被警戒雷达网发现的概率，为组网雷达信息融合中心综合网内所有雷达的探测概率分析计算得到；

PD：飞机被警戒雷达网发现的累积探测概率；

Talarm：警戒雷达网发现飞机时给出的预警时间；

x：飞机的状态向量，x∈X，X为状态空间；

xinit，xexit：飞机在进入点和退出点的状态向量；

Je（xa，xb）：飞机从状态xa飞到状态xb的最优代价，由局部最优低可探测性轨迹规划器负责计算。由于飞机带有非完整性约束，Je（xa，xb）通常为非对称的，即∃xa，xb∈X，Je（xa，xb）≠Je（xb，xa）。

为了进一步优化突防轨迹的综合效能，定义3个部分的优化目标函数［20］：

（1）最小化飞机被警戒雷达网发现的累积探测概率PD；

（2）最小化警戒雷达网发现飞机时给出的预警时间Talarm；

（3）最小化总的飞行油耗Mfuel。

综合这三方面，建立多目标的优化函数：

其中ω1，ω2，ω3为权重系数，根据任务态势、规划员意图、专家规则来确定。

LOTPANA问题可形式化如下：

其中，状态xj，（j=1，…，p）为决策变量。规划目标为式（9）定义的多目标，约束包括飞机的非线性动力学约束，飞机控制量约束，低可探测性对探测概率的约束，边界条件的约束。上述问题求得最优解后，即可得到最佳的飞机飞行航迹。可见，LOTPANA为一个复杂的多目标非线性连续时间的最优控制问题。

3　低可探测性轨迹规划求解框架

对LOTPANA问题采用Radau伪谱法求解［16-17］。低可探测性轨迹规划算法如图5所示。

图5　基于伪谱法的低可探测性轨迹规划求解框架

Step 1：建模。①建立问题的约束模型，包括：飞机动力学模型及约束、油耗模型、雷达探测概率模型、具体雷达探测波段下的飞机RCS模型、时序约束、低探测概率约束与低径向速度约束。②按照LOTPANA的定义的多目标，分别形式化各子优化目标；然后确定各子目标权重，定义其加权和为综合优化目标。

Step 2：离散化。①对LOTPANA依据雷达部署给出初始启发式的暴露段、低探测概率段及低径向速度段的划分。②将定义好的LOTPANA问题进行伪谱离散化，把连续的轨迹规划问题转化为有限维NLP问题。

Step 3：求解NLP问题。①采用SNOPT［18-19］求解转换后的NLP问题，达到设定的求解精度或迭代次数，判断规划解是否收敛；②得到规划的隐身轨迹，进而计算各雷达对作战飞机沿轨迹飞行全过程的瞬时探测概率，并对结果进行分析。

4　想定与实验

通过两个想定的2D仿真实验来验证本文所建立的模型及提出的方法的有效性，并对仿真结果作出分析。

想定1为5个雷达组网的场景。设置各雷达的性能参数一致，雷达的位置分别为RA（-20，60），RB（-10，-40），RC（55，45），RD（65，-50），RE（110，12），雷达的纵坐标都为0，其探测角度均为360°。另外添加飞机的过载约束、时间约束、速度约束、飞行范围约束等相关的约束。设置飞机起始位置为（-50，-5），航向角10°；结束位置为（170，20），航向角30°。当组网雷达的融合概率大于0.5以上时认为飞机被雷达发现，航迹仿真结果如图6所示，飞机的过载变化如图7所示，飞机在暴露段被雷达发现的概率如图8所示。

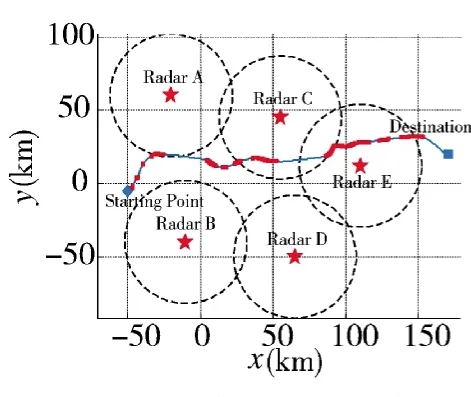
图6　想定1生成的航迹

图7想定1飞机过载

图6中蓝色实线为规划的隐身轨迹，该轨迹上的红色粗线段为飞机被雷达网探测发现的暴露段，虚线圆圈为该雷达对RCS为1 m2的目标的探测范围。飞机根据雷达的探测进行机动飞行，力图使得飞机以综合RCS较小的方位角朝向雷达。从图7中飞机在机动飞行时的过载在可用过载的范围内，同时从图8中可以看出飞机暴露段的时间较短，小于40 s；第3、4次暴露的总时间段为45 s，之后成功隐身；两次暴露之间的隐身时间段较长，足以使雷达丢失目标而重新搜索。总体来说在想定1中，航迹对综合任务效能进行了优化，隐身效果较好，可以成功抵达目的状态，可以在较短时间内进行轨迹规划。

图8　想定1飞机暴露时概率

想定2在想定1的基础上增加了一组双基地雷达，发射端在（-95，0），接收端在（-25，0），纵坐标都为0，利用极坐标系画出双基地雷达对RCS为1m2的目标的探测范围为Cassini卵形线［15］，添加相关的约束。设置飞机起始位置为（-130，-40），航向角10°；结束位置为（170，70），航向角30°。航迹仿真结果如图9所示。飞机的过载变化如图10所示，飞机在暴露段被雷达发现的概率如图11所示。

图9　想定2生成的航迹

图10　想定2飞机过载

结果表明，添加了双基地雷达后，依然可以规划出可行的飞行路线。图9、图10中可以看出，为了躲避雷达的探测，飞机飞行过程中同样经过了多次的机动飞行，横向激动次数明显比想定1中增多。图11中显示飞机被雷达发现的时间所占总时间比例较小，两次暴露之间的隐身时间段较长，足以使雷达丢失目标而重新搜索。总体来看，即使增加了双基地雷达，规划算法依然能在较短时间内规划处出实际可飞行的航迹。

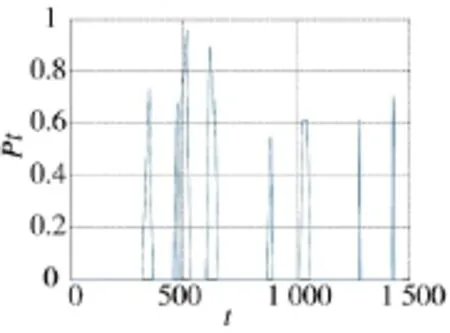
图11　想定2飞机暴露时概率

5　结论

本文主要针对隐身飞机对警戒雷达网突防问题，研究了警戒雷达组网对隐身飞机的探测和飞机的突防航迹规划两方面，基于单基地雷达和双基地雷达数学模型，进一步建立了组网警戒雷达信息融合模型；将隐身飞机低可探测性轨迹规划问题运用数学描述形式化，考虑突防轨迹综合效能，从而将LOTPANA描述为一个复杂的多目标非线性连续时间的最优控制问题；并提出了基于伪谱法的低可探测性轨迹规划方法。通过两个想定分别从对单基地组网雷达和单、双基地组网雷达的成功突防的仿真实验，飞机在飞行过程中通过自身姿态变化机动飞行降低被雷达发现对方概率和时间，充分验证了该模型和轨迹规划方法的可用性，为以后的进一步研究打下了基础。

［1］马云红，周德云.飞行器低空突防威胁建模与航迹优化算法［J］.火力与指挥控制，2004，29（5）：31-33.

［2］刘明华.基于遗传算法的飞行器路径规划研究［J］.现代电子技术，2008，18（4）：64-67.

［3］唐强，张新国，刘锡成.一种用于低空飞行的在线航迹重规划方法［J］.西北工业大学学报，2005，23（2）：271-275.

［4］姚远，周兴社，张凯龙，等.基于稀疏A*搜索和改进人工势场的无人机动态航迹规划［J］.控制理论与应用，2010，27（7）：953-959.

［5］黄超会，史宗鹏.巡航导弹航迹规划中雷达探测盲区的快速构造算法［J］.火力与指挥控制，2010，35（1）：88-90.

［6］LIY，HUANG J，HONG S，et al.A new assessmentmethod for the comprehensive stealth performance ofpenetration aircrafts［J］.Aerospace Science and Technology，2011，15（7）：511-518.

［7］张云飞，马武哲，张考.两种隐身飞机模型的雷达散射特性测试与分析［J］.北京航空航天大学学报，2003，29（2）：147-150.

［8］黄沛霖，姬金祖，武哲.飞行器目标的双站散射特性研究［J］.西安电子科技大学学报，2008，35（1）：140-143.

［9］王小谟，匡永胜，陈忠先.监视雷达技术［M］.北京：电子工业出版社，2008.

［10］张铁.偏微分、积分方程的有限元方法［M］.北京：科学大学出版社，2008.

［8］斯蒂芬·哈格，梅芙·卡明斯，埃米·菲利普斯.信息时代的管理信息系统［M］.6版.严建援，译.北京：机械工业出版社，2007.

［9］宋晓莉，余静，孙海传，等.模糊综合评价法在风险评估中的应用［J］.微计算机信息，2006，22（3）：71-73.

［10］查先进，陈明红.信息资源质量评估研究［J］.中国图书馆学报，2010，36（3）：46-55.

［11］秦继荣.指挥与控制概论［M］.北京：国防工业出版社，2012.

［12］SHANNON C E.A mathematical theory of communication［J］.The Bell System Technical Journal，1948，27（6）：379-423 and 27（10）623-656.

［13］赵振宇.关于建立社会科学成果评价机制的几个问题［J］.探索，2004，20（2）：92-95.

［14］王兵，权冀川.如何做好满意度调查问卷的设计［J］.学习导刊，2015，31（3）：56-60.

［15］权冀川，刘必欣，张童.指挥与控制系统信息资源评估指标研究［C］//第二届中国指挥控制大会论文集.北京：国防工业出版社，2014：92-95.

［16］曾宝昌，薛淑梅，任连芝.层次分析决策法及其应用研究［J］.内蒙古工业大学学报（社会科学版），1998，8（1）：66-74.出版社，2009.

［11］于荣欢，吴玲达，瞿师.组网雷达探测能力的并行计算与可视化方法研究［J］.系统工程与电子技术，2011，33（11）：2513-2517.

［12］陈璟，陈少飞，刘鸿福.基于RCS的三维低可探测性轨迹优化方法［J］.国防科技大学学报，2012，34（03）：89-93.

［13］BARR R S，SAMPSON M T.Qualitative assessment report portable-flightplanning software（PFPS）［R］.1997.

［14］M.S.A coincidence procedure for signaldetection［J］.IEEE Transactionson Information Theory，1956，2（1）：123-129.

［15］吴剑，喻玉华，周继强，等.隐身突防时战场环境建模与威胁分析［J］.火力与指挥控制，2011，36（11）：60-64.

［16］张煜，张万鹏，陈璟等.基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划［J］.航空学报，2011，32（7）：1240-1251.

［17］王铀，赵辉，惠百斌，等.利用Radau伪谱法求解UCAV对地攻击轨迹研究［J］.电光与控制，2012，19（10）：50-53.

［18］Philip E G.An SQP algorithm for large scale constrained optimization［J］.SIAM Review，2005，47（1）：99-131.

［19］Holmström K，Göran A O，Edvall M M.Users guide for TOMLAB/SNOPT［M］.Västerås，Sweden：Mälardalen University，Dept.ofMathematicsand Physics，2006.

［20］郭琳，周德云，汪凌霄.低可探测性飞机威胁建模及航迹规划仿真研究［J］.计算机仿真，2009，26（02）：89-92.

Low Observability Trajectory Planning for Stealth Aircraft PenetratesNetted Radars

LIUHong-fu，ZHOUWen-hong，CHENShao-fei
（School ofMechatronics Engineering and Automation，National University of Defense Technology，Changsha 410073，China）

To achieve low observability trajectory planning for stealth aircraft penetrates netted surveillance radars，the properties in penetrating process are analyzed firstly.And it establishes an information fusion model depending on themodels ofmonostatic radar and bistatic radar system.Then the trajectory planning problem is described with a mathematical method into an optimal control problem of complex multi-objective nonlinear continuous time，which considers the stealth ability，warning time and the fuel consumption with various restrictions.After that，the meyhod based on pseudospectralmethod is put forward for the low observability trajectory planning problem.Simulation results achieves the low observability trajectory planning for stealth aircraft penetrates netted surveillance radars and demonstrate the feasibility and availability of the proposedmethod.

netted surveillance radars，low observable，information fusion model，pseudospectral method，trajectory planning

V249.12

A

1002-0640（2016）09-0036-05

2015-07-16

2015-08-09

国家自然科学基金（61403411）；湖南省优秀研究生创新基金（No.CX 2013B013）；国防科技大学优秀研究生创新基金资助（No.B130302）

刘鸿福（1983-），男，湖南衡阳人，博士。研究方向：人工智能、任务规划。