地铁站Y型通道内行人汇集流交通特性

邱 果，宋 瑞，何世伟，邹彦雯

（1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京 100044；2.北京交通大学交通运输学院，北京 100044）

地铁站Y型通道内行人汇集流交通特性

邱 果1，宋 瑞2，何世伟2，邹彦雯1

（1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京 100044；2.北京交通大学交通运输学院，北京 100044）

为探索地铁站汇集通道内行人流密度的变化特征，建立改进偏随机步行者格子气模型来模拟开放边界条件下高峰期Y型通道内行人流汇集过程，模型由正方形与三角形格子组成，并利用QT编程仿真以任意角度相交的通道内的行人流.通过分析分支通道与汇集通道内行人流密度的相变规律特征，得到密度变化相图.研究证明汇集通道内行人流密度随分支通道宽度及偏移角度的变化关系，并结合理论推导证明仿真结果的准确性.研究发现:对于分支通道宽度相同的Y型通道，当分支通道行人流密度分别为0.4和0.3时，汇集通道内行人流发生拥挤过度，此时汇集处行人流密度约为0.5；但当分支通道宽度不同时，Y型通道汇集处发生拥挤的临界密度随分支通道宽度比值增大而减小，且随偏移角度增大而增大.

Y型通道；行人汇集流；相变规律；格子气模型；模型仿真

近年来，城市轨道交通以高效、快捷、准点等优势逐步成为市民出行的首选交通工具，步行通道是地铁站内乘客换乘、集散的主要设施，而Y型通道因存在两股汇入行人流的交织、冲突，客流高峰期在汇集处易受通道宽度限制而发生交通拥挤.格子气模型利用元胞自动机的动态特征来模拟流体粒子的运动，将宏观和微观交通模型有机结合，被广泛用于模拟行人流运行.Masakuni等［1-2］利用偏随机步行者格子气模型研究行人逆流、十字交叉处等情况下的行人流拥塞过渡问题.Yusuke等［3-4］运用偏随机步行者格子气模型探讨T型交叉口、大厅等行人疏散过程中的临界密度.Guo等［5］结合格子气模型与社会力模型的优势来模拟公共建筑中单一出口时的行人疏散过程.Akiyoshi等［6］利用平格子和转弯格子模型来模拟移动物体单向流的旋转运动.Fang等［7］利用改进格子气模型研究火车站带行李旅客的移动特性.Huo等［8］使用拓展格子气模型分析地板与楼梯接口处行人汇集流的移动特性.Shang等［9］提出考虑行人可变步长的拓展格子气模型.Yu等［10］基于格子气模型和地板场模型来模拟在单一出口和多障碍的房间内行人的疏散情况.岑华舵［11］利用格子气模型研究视觉和潜意识行为对通道内双向行人交通流的影响.李明华等［12］利用考虑行人移动偏好特性的格子气模型研究对向行人流中行人密度的分层现象.郭细伟等［13］利用异质格子气模型来模拟火灾情况下地铁人群疏散过程.马新露等［14］提出行人过街格子气模型研究有倒计时信号控制人行横道的行人过街特性.但是，目前的研究多是选择正方形格子模拟矩形空间内的行人运动，鲜有关于斜向相交区域的格子气模型及Y型通道内汇集行人流随通道宽度与偏移角度的变化关系研究.本文将正方形与三角形格子相结合，建立偏随机格子气模型来模拟高峰期Y型通道内2股分支行人流斜交汇入单一疏散出口的情况.模型可作为任意角度相交行人流普适模型.通过分析高峰期不同密度分支行人流汇集过程中Y型通道内汇集行人流密度的变化特性，可绘制Y型通道行人流密度相图，并研究汇集处行人拥塞临界宽度与分支通道宽度及偏移角度的关系.研究成果可为地铁站内步行通道设计及高峰期合理限流提供依据.

1　模型

1.1模型的构建

本文建立开放边界条件下Y型通道行人流汇集模型，见图1（以θ=45°为例）.模型被定义在L× H的区域中，L是Y型通道水平方向的长度，H为Y型通道竖直方向的高度.Y型通道由水平方向和斜向下（θ=45°）方向的2条分支通道相交组成.将模型系统分为4个部分，通道A为正方形区域eabf，通道B为平行四边形区域bdhg，汇集通道C为正方形区域acdb，出口通道D为正方形区域cijd.模型不考虑通道长度的影响，为简化设计，将水平通道宽度设为WA，通道B的宽度设为WB，通道A、D的水平长度及通道B的竖直高度均设为WA，通道C的大小随通道A、B的宽度变化而变化，WA、WB表示通道内允许并排行走的最大行人数.模型将水平主通道空间分成大小相同的正方形小格，以蓝色圆点表示来自通道A的行人，行人位于格子交叉处并沿正方形边长移动；而分支通道空间被分成等腰直角三角形小格，以红色圆点代表来自通道B的行人，行人位于格子交叉处并沿等腰直角三角形斜边移动.设计模型的格子大小为0.6 m×0.6 m，1 s走2格，即速度为1.2 m/s，模型中1个圆点仅代表1个不后退的偏随机步行者，格子每交叉点上仅容纳1个行人，行人不能重叠，且不考虑行人的体积.图1中箭头表示行人的最佳运动方向.

1.2模型的更新规则

仿真开始时行人分别从通道A的左侧和通道B的底部进入系统.模型由2类格子气模型组成，以实现Y型通道斜向相交.通道A内正方形格子上右行者的所有可能行走方式如图2（a）所示，通道B内等腰直角三角形格子上右上行者的所有可能行走方式如图2（b）所示.叉点代表此位置被其他行人占用，通道A内行人向前、左、右3个方向的移动概率分别用QAi，x，QAi，y，QAi，-y表示，通道B内行人向右上、左上、右下3个方向的移动概率分别用QBi，x，QBi，y，QBi，-y表示，通道A、B内不同行走方式对应的行人移动概率分别如表1、2所示.其中，i表示行人走行步数，D表示行人的移动偏好强度，且0＜D＜ l，当D=1时，行人移动的确定性最强；D=0时，行人移动的确定性最弱；随着D的增加，行人移动的确定性增加，D在不同位置取值不同，本文不考虑行人的偏好特性，即取D=0.

表1　通道A中不同行走方式下右行行人的移动概率Table 1 Transition probabilities of the right walker in Channel A under different configurations

当通道A中的行人向右行走经边界ab在交叉区域acdb（即汇集通道C）与通道B内向右上方行走经边界bd的行人发生交汇时，通道A中的行人将保持原有的行走规则继续移动，而通道B中的行人将改变原有的行走规则并按通道A内行人的行走规则移动，但是，根据走行习惯，行人不会在经过边界bd后立即向右行，而是以右上方为行走的偏好方向逐渐向右转变，因此，通道B中行人在汇集通道C中所有可能的行走方式，见图2（b）.与通道A内行人移动概率相比，通道B内前3种状态行人向各个方向的移动概率发生变化，见表2.

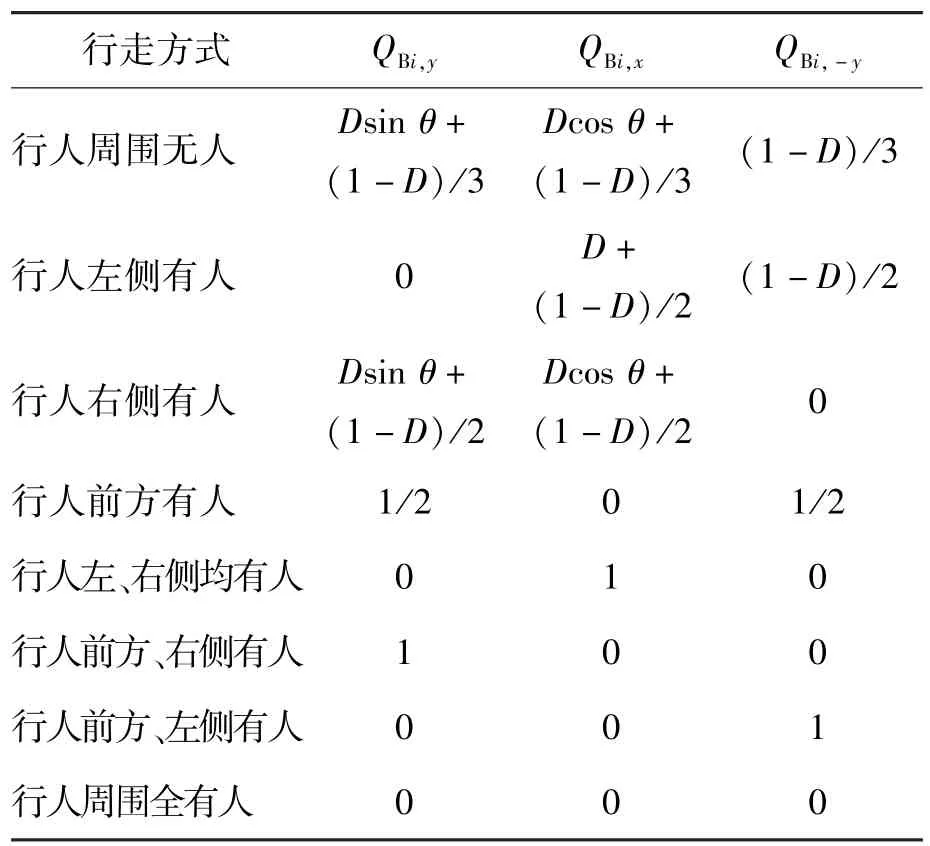
表2　通道B中不同行走方式下右行行人的移动概率Table 2 Transition probabilities of the right walker in Channel B under different configurations

表2中，QBi，x、QBi，y、QBi，-y分别表示通道B内行人向前、左、右3个方向的移动概率，θ为两相交通道之间的夹角.

模型采用并行更新机制，在仿真模型的演化规则中，每个行人都必须遵守如下行人移动规则:

1）单位时间步长t内，每个行人只能移动1个格子的长度.

2）在行人选择下一目标位置时，当存在多个空格子可供选择时，行人在这些格子中以相同的概率随机选择1个作为自己的下一步目标位置.

3）由于1个格子交叉点只能容纳1个行人，因此，在模型演化过程中，存在多个行人竞争同1个空格子的位置冲突问题.此时，系统将会以相等概率随机选择1个行人占据该位置，被选择的行人在下一步内移动到目标位置，没有被选中的行人将保持原来的位置不变.

2　仿真过程

本文以通道夹角45°为例进行仿真研究.在仿真研究中，通道行人流密度K定义为某时刻通道内含有的行人总数与通道面积内可容纳的最大行人数的比值，以KA、KB、KC、KD分别表示通道A、B、C、D内行人流的平均密度.最初，行人流以给定的初始密度KA和KB随机分布在通道A和通道B中.行人按上述行走规则由通道A、B向通道C、D移动，当某一行人通过通道D时，该行人将被移出系统.系统内行人每单位时间步长仅更新1次，更新过程服从上述规则.更新后，当通道A、B内的行人流密度分别低于KA和KB时，需向通道A、B入口加入行人流量以保证通道内行人流密度保持恒定，通道行人流量Q定义为单位时间步长内通过系统单位边界的行人数量.针对通道C的汇集行人流密度、流量公式为:

式中:t表示时间步长的计数；TCt表示t时刻通道C内含有的行人总数；PAt表示t时刻通道A中经边界ab进入通道C的人数；TBt表示t时刻通道B中经边界bd进入通道C的人数；TDt表示t时刻通道D内含有的行人总数；TD（t-1）表示t-1时刻通道D内含有的行人总数.使用计算机编程语言工具Qt Creator编写格子气模型行走规则并建立模型，对Y型通道内行人流汇集过程进行仿真并利用MATLAB处理仿真结果.

3　结果分析

3.1KA、KB和KC的相图

通过模拟高峰期Y型通道内行人流汇集过程发现，当分支通道内行人流密度逐渐增大并同步变化时，Y型通道汇集处行人流从低密度的自由流状态逐渐向高密度的拥挤状态转变，转变发生在临界密度处.将汇集通道行人流密度KC随分支通道初始行人流密度KA和KB的变化关系绘制在三维图中，即可得到Y型通道行人流汇集前后密度的相变规律，见图3.以（KA，KB，KC）为相空间的三维相图包含4个区域.在KA＜0.4且KB＜0.3的区域内，通道A、B、C内行人均处于自由流状态，汇集通道行人流密度KC随2分支通道密度KA、KB的增大而增大；在KA≥0.4且KB＜0.3的区域内，通道A中为拥挤流，而通道B中为自由流，此时通道C内汇集行人流密度为0.5；在KA＜0.4且KB≥0.3的区域内，通道B中为拥挤流，而通道A中为自由流，此时通道C内的汇集行人流密度为0.55；在KA＞0.4且KB＞0.3的区域内，通道A与通道B均处于拥挤状态.

3.2汇集通道行人流密度KC与通道宽度及偏移角度的关系

以W′B=WB/sinθ表示分支通道宽度WB在水平方向的分量，选择通道宽度WA和W′B分别为11～31的不同值进行实验，利用模型仿真来探索高峰期Y型通道内汇集行人流密度随分支通道宽度的变化情况.图4显示Y型通道在不同分支通道宽度情况下行人流汇集过程的仿真快照图，θ=45°，KA=KB=0.5，i=50.

仿真过程中，将通道A、B的行人流密度KA和KB设为从0.1～1以0.1为间隔的相同值并同步变化，偏移角度θ取45°，通过改变分支通道宽度及偏移角度，记录模拟过程中汇集行人流密度KC的变化情况，并绘制KC与通道宽度及偏移角度的变化关系曲线，见图5、6.令W*=W′B/WA，图5显示当θ=45°时，在自由流状态下，KC随分支通道内行人流初始密度之比的增大快速上升直至饱和，当0＜W*≤1时（见图5（a）），此时W′B不变，在KA、KB均为0.1时，KC随WA增大而增大，在KA、KB从0.1～0.3变化时，KC快速增大，在KA、KB均大于0.3并同步增长时，KC趋于稳定，随WA增大而增长缓慢；而当W*≥1时（见图5（b）），此时WA不变，在KA、KB从0.1～0.3变化时，KC快速增大，且KC随W′B增大而减小，在KA、KB均大于0.3并同步增长时，KC减小速度逐渐缓慢，当W*＞11/25后，随着W′B增大，对应于不同W′B的KC曲线几乎重叠.综上，汇集通道行人流密度KC随通道A宽度WA增大而增大，随通道B宽度水平分量W′B增大而减小.图6显示当WA=W′B=11时，汇集通道行人流密度KC随通道偏移角度θ的增大而增大，在KA、KB从0.1～0.4变化时，KC快速增大，且KC随θ的增大而增大，在KA、KB均大于0.4并同步增长时，KC增长速度较缓慢，且随θ变化趋于一致，总体来看，KC随θ增大而增长.

为了明确汇集通道拥挤时行人流临界密度与通道宽度及偏移角度的关系，做以下2点简化假设:

1）系统t时刻行人的运动仅与t-1时刻的行人运动有关.

2）当某一时刻通道密度达到饱和时，该时刻进入通道的人数等于离开通道的人数.

基于以上假设，当通道汇集处发生拥挤时，单位时间步长内进入通道C的人员数量Ni可表示为

而拥挤发生时，单位时间步长内从通道C向出口通道疏散的人员数量No可表示为

根据假设2，当通道汇集处发生拥挤时有Ni= No，联立式（3）（4），可以得到Y型通道内汇集流临界密度公式为

由式（5）可知，Y型通道汇集处发生拥挤的临界密度取决于分支通道宽度与偏移角度双重因素.当偏移角度θ=90°，即通道垂直相交时，Y型通道内汇集流临界密度取最大值，此时K*C仅与分支通道宽度的比值有关.当通道偏移角度确定时，Y型通道内汇集流临界密度KC随水平通道宽度WA增大而增大，随斜向通道宽度WB增大而减小；当分支通道宽度相同时，Y型通道内汇集流临界密度随分支通道偏移角度θ增大而增大，由此可见模拟结果显示出与推导结果一致的特征.

4　结论

以正方形与三角形格子相结合的偏随机步行者格子气模型模拟任意角度斜交的Y型通道内不同汇入密度条件下通道汇集处行人流的集散过程，通过改变行人输入密度、通道宽度及偏移角度，以模型输出的汇集流密度绘制分支通道与汇集通道行人流密度关系相图，并研究汇集流密度随通道宽度及偏移角度的变化情况.研究得到以下结论:

1）对于给定形式的Y型通道，汇集处行人流从自由流状态到拥挤排队状态过渡发生在分支通道行人流密度达到临界密度处，此时汇集通道内行人流密度为0.5左右.

2）当改变Y型通道两分支通道宽度及偏移角度时，汇集通道内行人流密度随分支通道宽度比值的增大而减小，随偏移角度的增大而增大.

3）推导出Y型通道内汇集流临界密度与通道宽度及偏移角度的关系式.

研究成果可为进一步研究斜交区域内行人流冲突及考虑行人偏移特性的相交通道行人移动特性等提供依据.

［1］MASAKUNI M，TUNEMASA I，TAKASHI N.Jamming transition in pedestrian counter flow［J］.Physica A: Statistical Mechanics and its Applications，1999，267（3/4）:487-498.

［2］MASAKUNI M，TAKASHI N.Jamming transition of pedestrian traffic at a crossing with open boundaries［J］.Physica A:Statistical Mechanics and its Applications，2000，286（1/2）:377-390.

［3］YUSUKE T，TAKASHI N.Scaling behavior of crowd flow outside a hall［J］.Physica A:Statistical Mechanics and its Applications，2001，292（1/2/3/4）:545-554.

［4］YUSUKET，TAKASHIN.Cloggingtransitionof pedestrian flow in T-shaped channel［J］.Physica A: Statistical Mechanics and its Applications，2002，303（1/2）:239-250.

［5］GUO R Y，HUANG H J.A mobile lattice gas model for simulatingpedestrianevacuation［J］.PhysicaA: Statistical Mechanics and its Applications，2008，387（2/3）:580-586.

［6］AKIYOSHI M，TAKASHI M，TAKASHI N.Traffic flow of mobile objects through obstacles:turning and translational objects［J］.Physica A:Statistical Mechanics and its Applications，2009，388（2/3）:157-173.

［7］FANG Z M，LV W，JIANG L X，et al.Observation，simulation and optimization of the movement of passengers with baggage in railway station［J］.International Journal of Modern Physics C，2015，26（11）:1-15.

［8］HUO F Z，SONG W G，LV W.Analyzing pedestrian merging flow on a floor-stair interface using an extended lattice gas model［J］.Simulation:Transactions of the Society for Modeling and Simulation International，2014，90（5）:501-510.

［9］SHANG H Y，HUANG H J，ZHANG Y M.An extended mobile lattice gas model allowing pedestrian step size variable［J］.Physica A:Statistical Mechanics and its Applications，2015，424:283-293.

［10］YU X Q，CHANG R R，ZHANG C H.Evacuation of pedestrians using lattice gas model and floor field model［C］//2014 International Conference on Audio，Language and Image Processing（ICALIP）.New Jersy:IEEE，2014:812-816.

［11］岑华舵.考虑视觉和潜意识作用的行人流格子气模型的研究［D］.南宁:广西大学，2013.CEN H D.Study of lattice-gas models of pedestrian flow by considering the effects of sights and subconscious［D］.Nanning:Guangxi University，2013.（in Chinese）

［12］李明华，袁振洲，许琰，等.基于改进格子气模型的对向行人流分层现象的随机性研究［J］.物理学报，2015，64（1）:1-12.LI M H，YUAN Z Z，XU Y，et al.Randomness analysis of lane formation in pedestrian counter flow based on improved lattice gas model［J］.Acta Physica Sinica，2015，64（1）:018903-1-12.（in Chinese）

［13］郭细伟，陈建桥，魏俊红.格子气模型在地铁站人群疏散运动中的应用［J］.武汉理工大学学报（交通科学与工程版），2014，38（3）:567-571.GUO X W，CHEN J Q，WEI J H.Application of lattice gas model to pedestrian evacuation from subway station［J］.JournalofWuhanUniversityofTechnology（Transportation Science&Engineering），2014，38（3）: 567-571.（in Chinese）

［14］马新露，孙惠芳.信号控制人行横道格子气行人仿真模型［J］.交通运输系统工程与信息，2014，14（4）: 59-65.MA X L，SUN H F.Lattice gas simulation model of pedestrian at signalised crosswalks［J］.Journalof TransportationSystemsEngineeringandInformation Technology，2014，14（4）:59-65.（in Chinese）

（责任编辑 郑筱梅）

Characteristics of Pedestrian Merging Flow in the Subway Y-shaped Channel

QIU Guo1，SONG Rui2，HE Shiwei2，ZOU Yanwen1
（1.State Key Laboratory of Rail Traffic Control and Safety，Beijing Jiaotong University，Beijing 100044，China；2.School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China）

To explore the variation of pedestrian density in the merging channel of subway station，a modified lattice gas model with biased random walkers was proposed to simulate the aggregation process of pedestrian flows in Y-shaped channel in peak time under open boundary conditions.The model consisted of square and triangular lattices，and QT simulation program was used to mimic the pedestrian flow in channels intersected at any angle.By analyzing the phase transition characteristics of pedestrian flow densities in both branch channels and merging channel，the density phase diagram was obtained.Studies show that the pedestrian flow density of the merging channel changed with variation of the width and offset angle of the branch channels，combined with theoretical analysis to prove the accuracy of the simulation results.It is found in the study that for a Y-shaped channel with the same branch channel width，the dynamic transition of Y-shaped channel occurs at density of branch channel is 0.4 and 0.3 respectively，and the merging channel density is at around 0.5，but when the widths of branch channels are not the same，the critical density of merging flow decreases with the channel width ratio increase and increases with the offset angle increase.

Y-shaped channel；pedestrian merging flow；phase transition；lattice gas model；model simulation

U 491

A

0254-0037（2016）10-1526-06

10.11936/bjutxb2015120043

2015-12-17

国家“973”计划资助项目（2012CB725403）

邱 果（1990—），女，博士研究生，主要从事交通运输规划与管理方面的研究，E-mail:14114250@bjtu.edu.cn