基于混沌果蝇优化最小二乘支持向量机的秸秆发酵过程软测量建模
2016-10-18朱湘临华天争
朱湘临,华天争
(江苏大学电气信息工程学院,江苏镇江 212013)
基于混沌果蝇优化最小二乘支持向量机的秸秆发酵过程软测量建模
朱湘临,华天争
(江苏大学电气信息工程学院,江苏镇江 212013)
针对秸秆发酵制取燃料乙醇过程的关键参量乙醇质量浓度难以用传统物理传感器实时在线测量,给发酵过程的监测与控制带来困难这一难题,采用混沌果蝇优化算法(chaos fruit fly optimization algorithm,CFOA)优化最小二乘支持向量机(least square support vector machine,LSSVM)的关键参数,避免了普通交叉验证法选取参数的耗时性和盲目性,建立混沌果蝇最小二乘支持向量机软测量模型,实现乙醇质量浓度的在线实时测量.实验仿真表明:基于CFOA的LSSVM模型平均误差为4.55%,明显优于LSSVM模型,表明该软测量建模方法预测能力强,测量精度高.
秸秆;果蝇优化算法;最小二乘支持向量机(LSSVM);乙醇质量浓度
由于秸秆发酵制取燃料乙醇过程的机理复杂性和高度非线性,利用常规方法建立发酵过程的精确机理模型难度很大.菌体质量浓度、可发酵糖质量浓度以及乙醇质量浓度是反映秸秆发酵进程的关键参数,但实际中没有直接的在线实时测量器材[1],因此建立这些参数的软测量模型十分必要.通常这些参数的获取是经过实验室周期采样、离线操作、分析测定,取样间隔对获得的测量数值影响较大,且时滞大,不利于发酵过程的实时控制优化[2],而且在实际操作中,取样容易引起染菌,造成发酵产物产量和质量的下降.秸秆发酵过程相对于部分化学反应过程,反应条件温和,系统运行过程较为稳定,发酵过程是一个慢时变过程,可近似看作静态过程.支持向量机适合小样本学习,学习能力强,泛化能力优越,不过分依赖样本的数量和质量,利用其特点针对发酵过程进行软测量建模是解决以上问题的有效方法[3-6].
传统建模方法会遇到模型选择、维数灾难、局部极小值点等问题,标准SVM则在有限样本的情况下,算法的经验风险和推广能力得以兼顾,但其复杂性会因为样本的增加而加深[7-8].最小二乘支持向量机(least square support vector machine,LSSVM)方法是对标准SVM进行了优化,在目标函数中选用误差平方和项替换误差的绝对值项,降低了计算难度,解决了基本SVM计算过程复杂等问题[9].LSSVM的目标函数仅要解线性方程组,计算难度降低,有效提高了求解速度.在LSSVM建模过程时,正则化参数和核参数的优化设计尤为重要,它们直接关系到模型的拟合精度和泛化性能.目前常用的参数优化方法如人工免疫算法、混沌蚁群优化算法等能有效提高SVM的建模精度[10-14].果蝇优化算法(fruit fly optimization algorithm,FOA)通过模拟果蝇觅食的动作完成对最佳位置的获取,是基于随机搜索的全局优化算法,具有运算速度快、全局收敛效果好等优点[15].
本文将混沌算法与FOA相结合,由于混沌运动具有遍历性、随机性等特点,将其引入迭代寻优的搜索过程,对LSSVM模型中的2个关键参数组合寻优,建立了基于混沌果蝇优化的LSSVM软测量模型,基于秸秆发酵制取燃料乙醇实验数据,开展算法的仿真与验证研究.仿真结果表明:该方法能较好实现发酵过程乙醇质量浓度的实时测量.
1 LSSVM软测量建模
给定训练数据集{(xi,yi)|i=1,2,…,N},其中xi∈ RRn为系统的输入量,yi∈ RR为系统的输出量,LSSVM数学模型为
其约束条件为
式中:γ∈ RR+是惩罚参数;ξi=[ξ1,ξ2,…,ξn]T;ω为权向量;b为偏差量;φ(·)是一个非线性映射,能把xi从输入空间映射到高维(甚至无限维)的特征空间.
用Lagrange法求解优化问题
式中ai为Lagrange乘子.根据KKT条件将求解,最终可转换为求
式中:y=[y1,y2,…,yn];1=[1,1,…,1]T;a=[a1,a2,…,an]T;Ω是一个方阵,其第i行j列的元素为Ωi=φT(xi)φ(xj)=K(xi,xj),i,j=1,2,…,n;K(·)为核函数,选用径向基核函数
式中σ为核函数宽度.
可以用最小二乘法求出式(4)中的ai和b,最终得到LSSVM发酵过程软测量回归模型为
2 混沌果蝇优化
2.1FOA
果蝇是一种昆虫,其嗅觉敏锐,可较好地搜集漂浮着的食物气味,接近目标以后利用视觉得知目标和同伴的位置,然后朝该方向飞近.通过对其觅食行为进行模拟,可建立交互式的FOA[15].根据果蝇寻找目标的方式,FOA可总结成以下步骤:
1)确定种群大小与迭代次数上限,设定种群中单体个体数量m,随机地产生果蝇群体初始化位置Xaxis与Yaxis.
2)随机地产生单个果蝇寻找食物的方向和距离,保证种群所有单体的随机性,有
其中r为随机数.
3)初始状态下不清楚目标的位置信息,则求得果蝇个体和原点之间的直线距离,设其倒数是味道质量浓度的判定值,求得判定值Si,有
4)判定值Si代入味道判定函数,求解出各果蝇单体的对应的味道质量浓度
5)找到当前果蝇群体中Smelli最高的个体(求极小值),并记录该位置
6)记下当前代最佳味道质量浓度bestSmell和相应横纵坐标值,然后果蝇种群通过视觉向最佳位置逼近
7)开始迭代寻优,重复操作2)~5),同时判断bestSmell是不是比Smellbest更优,如果是,则跳转至6).
2.2混沌优化算法
混沌[16]是确定系统中出现的一种貌似无规则且复杂的运动形态,普遍存在于非线性系统中,具备随机性、遍历性、规律性.所以混沌能够进行寻优,并且可以防止过早地陷入局部极小进而提高搜索效率.本文采用Logistic混沌映射,其模型为
式中:μ为控制参量;z(0)∈[0,1].初值不包括混沌迭代方程的4个不动点(0,0.25,0.75,1).
当μ=4,取0<x<1,系统呈现着完全混沌的状态.设求解m维变量极小值问题
为混沌变量czi的一种推演等式,czi对应着Logistic映射的第i个混沌变量.
根据式(14)把czi从混沌变量区间[0,1]映射到对应的优化变量区间[ai,bi].
2.3混沌果蝇优化算法
FOA优点突出,但算法的收敛精度对初始取值很敏感,如果初值选择得恰当,收敛精度会比较高,一旦初值选定得不合适,迭代搜索时容易陷入局部最优,而且收敛精度不高.由于混沌运动的特点,将其引入迭代寻优过程中可以避免陷入局部极小[17].利用混沌序列对果蝇群体的位置进行初始化[18],提升种群多样化程度,加强搜索的遍历性.
混沌果蝇优化算法(chaos fruit fly optimization algorithm,CFOA)的步骤如下.
1)设置初始值:群体大小sizepop,迭代上限值maxgen,迭代次数gen.
2)混沌初始化,随机生成2个sizepop个果蝇的最初位置,用行向量zi表示(本文需要优化2个参数,故zi在本文中采用4维向量,前2位表示xi,后2位表示yi).
3)将所有zi的各个分量经过式(15)完成转换,映射为混沌变量czi,且czi∈[0,1].
4)把czi的各分量通过式(12)完成混沌操作,然后将各分量根据式(15)进行逆变换,变换成[ai,bi]间的普通变量zi.
5)根据FOA中的步骤3)计算出Disti,并由D(i,1)和D(i,2)表示,类似地,用S(i,1)和S(i,2)表示Si,且S(i,1)=1/D(i,1),S(i,2)=1/D(i,2).然后,代入Si至LSSVM的预测模型,设γ=60S(i,1),σ2=S(i,2),LSSVM模型的参数[γ,σ]由[S(i,1),S(i,2)]表示.依据预测结果,能够求得气味质量浓度Smelli,Smelli采用训练集的均方差为适应度值.获得最优适应度值对应的味道质量浓度Smellbest,以及对应的位置.
6)迭代数gen=gen+1,一旦达到停止条件,搜索行为终止,返回最优参数γ和σ,若没有达到,转至步骤2).
3 秸秆发酵过程的软测量模型的建立
3.1选取输入样本
秸秆发酵过程的工艺流程如图1所示.为了验证上述算法对秸秆发酵制取燃料乙醇过程软测量建模的可行性,本文基于KRH-100L-Y发酵系统平台开展实验研究,按照工艺提供的特定的配方配制培养基分批发酵实验.发酵罐蒸汽高温消毒后加入培养液,接种发酵菌种,接种量为5%,温度控制在37℃±1℃,通气量为0.08 L/min,搅拌转速控制为120~180 r/min.
通过对秸秆发酵制取燃料乙醇过程机理的分析,以发酵工艺的实际实验经验,选取能直接可测量且与过程密切相关的外部变量(发酵罐温度t、发酵罐压力p、电机搅拌转速r、发酵液体积V、空气流量l、CO2质量浓度μ、葡萄糖流加速率ρ、氨水流加速率η、溶解氧DO质量浓度、发酵液酸碱度pH),输出变量为乙醇质量浓度.由数字系统每隔1 h采集发酵过程的变量值,由下位机传送到上位机,形成数据库.在发酵正常工况下,每1 h取样1次发酵液,采用气相色谱法测试乙醇质量浓度.总共采集10个发酵批次的数据,在一个发酵周期取出1批数据(每批次数据含72个样本),取9批数据当作训练样本集,1批数据作为测试样本集.
式中:μij为两变量的相关系数;si、sj分别为不可测变量数据组和可测变量数据组;M为样本数.
式中:λij(k)为变化率关联系数;ζk为符号因子;rij为关联度;β为数据变化率对关联度的影响因子.
应用一致相关度分析,依照式(16)(17)计算采集的外部变量数据与输出变量的关联度,计算结果如表1所示.
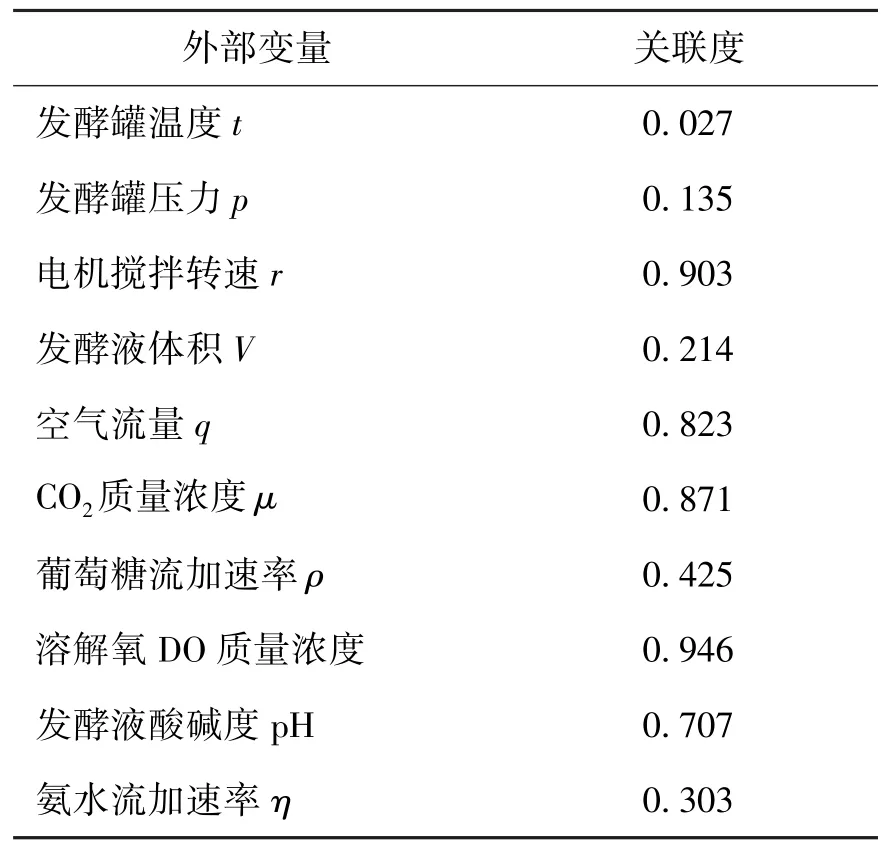
表1 环境变量和主导变量的关联度Table 1 Incidence degree between environmental variables and dominant variables
通过相关性分析和发酵过程经验,设定关联度值rij≥0.7的条件下,选取可测外部变量溶解氧质量浓度、发酵液酸碱度、CO2质量浓度、电机搅拌速度、空气流量作为辅助变量.
3.2CFOA-LSSVM软测量建模
本文将混沌运动与FOA有机结合,先通过混沌序列对果蝇位置进行初始化,避免FOA过早陷入局部最优解,再通过FOA获得较为精确的全局最优解,寻求最佳惩罚参数γ和核参数σ.CFOA-LSSVM建模方法如下:
1)针对现场采集的数据,存储成原始样本集,利用一致关联度法分析、确定模型的输入输出变量,输入向量X=[pH,DO,μ,γ,q].
2)对样本数据做预处理.
3)初始化参数γ和σ,构造线性回归函数对样本数据进行拟合,建立LSSVM模型.
4)用CFOA对参数γ和σ迭代寻优并重建回归模型,满足中断条件即到达迭代上限maxgen,停止搜索,结束后将最优参数γ和σ赋予LSSVM.
5)用测试样本集对模型进行仿真验证.
6)设置性能评价指标来评价预测结果以及估计模型的预测能力,其计算公式为
式中:yi为离线测量值;为模型预测值;n为预测数据的个数.
3.3模型的仿真验证和分析
3.3.1参数寻优仿真
为了验证FOA参数寻优的有效性,本文选用粒子群优化(particle swarm optimization,PSO)算法进行参数寻优作为参考,并与FOA寻优效果进行对比.把训练样本数据作为研究对象,分别采用CFOA和粒子群算法对LSSVM的惩罚参数γ和核参数σ进行寻优,先对比2种方式寻优的效率,再利用得到的2个重要参数建立LSSVM模型并根据此模型来做预测,进而验证所得参数的应用有效性.
图2为CFOA和PSO算法分别对LSSVM优化关键参数的曲线图.可见,当迭代到128代的时候,粒子群中最优的适应度值显现出来,对应的最低均方误差是2.5×10-4,而果蝇群体迭代到35代的时候,出现了最优的适应度值,对应的最低均方差是1.72×10-4,此时获得的优化参数[γ,σ]=[120,4.65].比较迭代曲线趋势图可以看出,CFOA较PSO寻优的速度更快,而且收敛的精度也更高.
图3为基于2种算法参数寻优的LSSVM模型对乙醇质量浓度的预测输出情况.比较预测输出曲线可以看出,2种方法的预测值都能较好地跟踪真实值,CFOA所建立的模型拟合程度稍优于PSO所建模型的拟合程度,说明CFOA-LSSVM软测量模型以较高的精度逼近真实值,与实际情况十分贴近,表明关键参数选取的正确和有效.
3.3.2乙醇质量浓度的预测仿真和分析
为了说明CFOA能够有效提高LSSVM的建模精度以及具有较强的预测能力,根据交叉验证法建立参数未经优化的LSSVM的秸秆发酵乙醇质量浓度预测曲线,如图4所示.从图4可以看出:CFOALSSVM预测结果基本和乙醇质量浓度的实验值一致,误差很小;而参数没有经过优化的LSSVM的乙醇质量浓度预测结果和乙醇质量浓度的实验值有较大的误差,表明CFOA-LSSVM对于该发酵过程乙醇质量浓度更加逼近于离线化验值,预测精度更高.
图5是CFOA-LSSVM建模方法和基本LSSVM模型2种方法的预测误差对比仿真图,可见采用混沌果蝇寻优参数建立的模型预测结果的变化范围较之参数不进行优化的基本LSSVM模型更小,逼近程度更优,CFOA-LSSVM建模的预测值在极小的误差范围内逼近实验测量值,具有更高的建模精度.
为了更好地比较秸秆发酵预测结果,仿真过程中计算了性能指标,如表2所示.从表2给出的2种建模方法的性能及预测误差对比来看,CFOALSSVM算法预测时的平均误差0.045 5显著低于用LS-SVM算法的平均误差0.234 3,同时均方差0.124 8明显低于LS-SVM均方差0.697 5,CFOALSSVM算法最大误差0.483 9也明显低于LS-SVM最大误差1.788 1,表明CFOA-LSSVM建模的预测性能更为优越,稳定性更强并且精度更高.

表2 2种方法所得参数与预测误差的对比Table 2 Performance comparisons of straw fermentation process
4 结论
1)针对常规交叉验证法选取LSSVM关键参数的耗时性和盲目性,将混沌优化引入FOA的迭代寻优过程,组合寻优的参数γ和σ.仿真结果显示,所提算法是选取LSSVM参数的一种有效方法,搜索效率高,有着较快的收敛速度以及较高的收敛精度,能高效地寻得所需参数.
2)针对秸秆发酵过程中乙醇质量浓度难以在线测量的难题,基于发酵控制系统平台的实验数据,建立CFOA-LSSVM秸秆发酵过程软测量模型,仿真验证了该算法用于秸秆发酵过程建模的有效性,优化后的模型能以更高的精度跟踪预测乙醇质量浓度.
[1]YUAN J Q,XU Y Y,HU K L,et al.On-line application orientedoptimalschedulingforpenicillinfed-batch fermentation[J].Chemical Engineering and Processing,2009,48(2):651-658.
[2]黄永红,孙丽娜,程浩.燃料乙醇发酵过程生物参量的软测量建模[J].控制工程,2014,21(2):263-267.HUANG Y H,SUN L N,CHENG H.Soft sensor modeling of biological parameters in the fuel ethanol fermentation process[J].Control Engineering of China,2014,21(2): 263-267.(in Chinese)
[3]顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报(自然科学版),2010,50(7): 1063-1066.GU Y P,ZHAO W J,WU Z S.Least squares support vector machinealgorithm[J].JournalofTsinghua University(Science&Technology),2010,50(7):1063-1066.(in Chinese)
[4]黄丽,孙玉坤,嵇小辅,等.基于CPSO与LSSVM融合的发酵过程软测量建模[J].仪表仪器学报,2011,32(9):2066-2070.HUANG L,SUN Y K,JI X F,et al.Soft sensor modeling of fermentation process based on the combination of CPSO and LSSVM[J].Chinese Journal of Scientific Instrument,2011,32(9):2066-2070.(in Chinese)
[5]张淑宁,王福利,何大阔,等.基于多最小二乘支持向量机的草酸钴粒度软测量[J].仪表仪器学报,2010,31(9):2081-2087.ZHANG S N,WANG F L,HE D K,et al.Soft sensor prcobalt oxalate partical size based on multiple LSSVM regression[J].Chinese Journal of Scientific Instrument,2010,31(9):2081-2087.(in Chinese)
[6]高学金,王普,孙崇正,等.一种建立发酵过程模型的新方法[J].北京工业大学学报,2006,32(5):405-409.GAO X J,WANG P,SUN C Z,et al.A new effective method on modeling for fermentation process[J].Journal of Beijing University of Technoology,2006,32(5):405-409.(in Chinese)
[7]VAPNIK V N.The nature statistical learning theory[M].New York:Springer-Verlag,1999:18-290.
[8]VAPNIK V N.An overview of statistical learning theory[J].IEEE Transactions on Neural network,1999,10(5):988-999.
[9]SUYKENS J A K,VANDEWALLE J.Least squares support vector machines classifiers[J].Neural Processing Letters,1999,10(5):1032-1037.
[10]YANG F G,WANG R L,WANG Y Q.Study onclassification performance and parameter optimization of least squares support vector machines[J].International Journal ofAdvancementsinComputingTechnology,2012,4(12):152-159.
[11]XIE C L,SHAO C,ZHAO D D.Parameter optimization ofleastsquaressupportvectormachinesandits application[J].Journal of Computers,2011,6(9): 1935-1941.
[12]王博,孙玉坤,嵇小辅,等.基于PSO-SVM逆的赖氨酸发酵过程软测量[J].化工学报,2012,63(9): 3000-3007.WANG B,SUN Y K,JI X F,et al.Soft-sensor modeling for lysine fermentation processes based on PSO-SVM inversion[J].CIESC Journal,2012,63(9):3000-3007.(in Chinese)
[13]张春晓,张涛.基于最小二乘支持向量机和粒子群算法的两相流含油率软测量方法[J].中国电机工程学报,2010,30(2):86-91.ZHANG C X,ZHANG T.Soft measurement method for oil holdup of two phase flow based on least squares support vector machine and particle swarm optimization[J].Proceedings of the CSEE,2010,30(2):86-91.(in Chinese)
[14]陈如清,俞金寿.基于粒子群最小二乘支持向量机的软测量建模[J].系统仿真学报,2007,19(22): 5307-5310.CHEN R Q,YU J S.Soft sensor modeling based on particle swarm optimization and least squares support vector machines[J].Journal of System Simulation,2007,19(22):5307-5310.(in Chinese)
[15]PAN W C.A new fruit fly optimization algorithm:taking the financialdistressmodelasanexample[J].Knowledge-Based Systems,2012,26:69-74.
[16]熊伟丽,姚乐,徐保国.混沌最小二乘支持向量机及其在发酵过程建模中的应用[J].化工学报,2013,64(12):4585-4591.XIONG W L,YAO L,XU B G.Chaos least squares support vector machine and its application on fermentation process modeling[J].CIESC Journal,2013,64(12): 4585-4591.(in Chinese)
[17]李霞,孙灵芳,杨明.基于改进FOA匹配追踪的超声信号处理研究[J].仪表仪器学报,2013,34(9): 2068-2073.LI X,SUN L F,YANG M.Research on ultrasonic signal processing based on improved FOA matching pursuit[J].Chinese Journal of Scientific Instrument,2013,34(9): 2068-2073.(in Chinese)
[18]周平,白广忱.基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J].航空动力学报,2013,28(5):1013-1018.ZHOU P,BAI G C.Robust design of turbine-blade low cycle fatigue life based on neural networks and fruit fly optimization algorithm[J].Journal of Aerospace Power,2013,28(5):1013-1018.(in Chinese)
(责任编辑 吕小红)
Soft Sensor Model for Straw Fermentation Process Based on Least Squares Support Vector Machine Optimized by Chaos Fruit Fly Algorithm
ZHU Xianglin,HUA Tianzheng
(College of Electrical and Information Engineering,Jiangsu University,Zhenjiang 212013,Jiangsu,China)
It is difficult to directly measure the product concentration by using traditional physical sensors during the straw fermentation process,which makes the monitoring and real-time control impossible.To resolve this problem,the chaos fruit fly optimization algorithm(CFOA)is introduced to least square support vector machine(LSSVM)to optimize some key parameters,which overcomes some shortcomings of the cross validation method such as time consuming and blindness in parameter selection.Using this way,the CFOA-LSSVM soft sensor model is built for the straw fermentation process,which realizes the real-time measure of product concentration in this process.The simulation shows that the average measurement error of the proposed CFOA-LSSVM soft sensor is 4.55%,which is smaller than the traditional LSSVM model.The proposed CFOA-LSSVM soft sensor model has strong forecasting capability and high accuracy.
straw;fruit fly optimization algorithm(FOA);least square support vector machine(LSSVM);ethanol concentration
TP 183
A
0254-0037(2016)10-1468-07
10.11936/bjutxb2016030039
2016-03-16
吉林省重大科技攻关专项(20140203005SF);江苏省科技支撑项目(BE2010354)
朱湘临(1963—),男,研究员,主要从事鲁棒控制、生物反应过程优化控制方面的研究,E-mail:zxl4390@126.com
