三旋翼飞行器的建模及其姿态自抗扰控制

阮晓钢，张晓锐，王丹阳

（北京工业大学电子信息与控制工程学院，北京100124）

三旋翼飞行器的建模及其姿态自抗扰控制

阮晓钢，张晓锐，王丹阳

（北京工业大学电子信息与控制工程学院，北京100124）

根据国内外旋翼飞行器的研究现状以及三旋翼飞行器的机械结构，对三旋翼飞行器进行力矩分析，建立数学模型.采用自抗扰控制方法对三旋翼飞行器的姿态角进行姿态控制，通过Matlab仿真与PID控制方法的对比试验，以及跟踪不同数值大小的阶跃响应信号进行分组仿真.仿真结果表明，自抗扰控制算法具有有效性和快速性，分组试验表明针对不同大小的阶跃信号，可采用不同的参数进行调节.结果表明:该方法既具有良好的滤波性与鲁棒性，又保留了PID控制的大体框架与结构简单等优势，在工程和之后的试验中有一定的指导价值.

三旋翼飞行器；数学模型；自抗扰控制；鲁棒性

小型旋翼飞行器具有广阔的军事和民用前景，近年来已成为国际上新的研究热点，当前国内外各高等院校及研究机构针对于三旋翼式无人飞行器的研究与开发尚处于起步阶段，大多数研究旋翼的实验室对小型飞行器的研究主要是基于四旋翼、六旋翼、八旋翼等具有对称结构的飞行器.迄今为止，四旋翼、六旋翼等具有对称结构飞行器在学术研究和工程应用上取得相当大的进展，在国外的旋翼飞行器中，如瑞士洛桑联邦科技学院OS4，使用4个超声波传感器探测障碍物、1个超声波传感器测高度，很好地实现了飞行器的避障功能；美国DragonflyerX4采用碳纤维螺旋桨，由4个无刷电机驱动，具有自动平衡及定点悬浮功能，由于自身结构轻便，平衡性在原有旋翼飞行器的基础上大大提高；在国内旋翼飞行器的研究中，国防科技大学的实验室通过利用DragonflyerX4旋翼的动力系统和瑞士Maxon电机与自己设计的齿轮减速装置结合的方式来开展针对于微小型四旋翼飞行器的研究工作.这些四旋翼飞行器都是国内外具有代表性的旋翼飞行器，已经具有很好的飞行性能与指标［1］.但是在关键技术的研究上，还有诸多的困难值得去挑战，如控制系统的最优化、机械电气结构的精简、旋翼飞行器的持续航行的时间、飞行姿态的精确控制等，这使其距离真正走向成熟达到实用要求还有一定的差距.

相比较于四旋翼飞行器，三旋翼飞行器具有结构简单、稳定性好、材料节省等优势.但由于三旋翼飞行器是一种不对称的结构的飞行器，因此它的力矩分析、动力学建模、姿态控制等与四旋翼大为不同.国内外对于三旋翼飞行器的研究尚处于待开发状态，本文在国内外相关研究基础上提出了三旋翼飞行器的研究方案，目的是为三旋翼飞行器的姿态控制研究提供有效途径并丰富无人机领域的发展［2］.

1　三旋翼飞行器的力矩平衡分析

在三旋翼飞行器飞行过程中，螺旋桨电机会产生2种力，如图1所示.一种是电机产生的扭转力f1、f2、f3，扭转力的方向可近似被认为是绕着l1、l2、l3为轴的方向；另一种力是3个电机产生的升力F1、F2、F3［3］，如图2所示，此组力为旋翼提供向上的力使飞行器在半空中能完成上下的飞行，升力的方向可近似看成是与l1、l2、l3端点接触，垂直于x-y轴方向向上.当飞行器处于悬停状态时，应当满足3个力矩的平衡条件使飞机不会绕着x、y、z轴转动.

第1个平衡条件，使三旋翼飞行器在悬停状态下不绕着z轴转动，f1、f2逆时针旋转，f3顺时针旋转，所以，可以得出平衡方程

第2个平衡条件，使三旋翼飞行器在悬停状态下不绕着x轴转动，F1、F2分别在x轴两侧，相反的力矩方向可以使飞行器不绕着x轴转动，可得到平衡方程

第3个平衡条件，使三旋翼飞行器在悬停状态不绕着y轴转动，且会产生一个与F1、F2产生的相反的力矩，可列出平衡方程

式中l0为飞行器的控制器配重O到重心O′的距离.

除上述的3个平衡条件之外，在悬停状态下还需要3个螺旋桨提供的升力大小平衡旋翼飞行器的重量，由此可列出平衡方程

式中mg为飞行器总重量（包括配重器）.

假设x轴为正方向，在悬停状态下x、y、z轴所受螺旋桨合力为［4］

单个电机可提供的升力为

式中:Ki为升力与转速平方的比例系数；Fi为单个电机可提供的升力.

单个电机可提供的扭转力为

式中:ki为升力与转速平方的比例系数；fj为单个点击可提供的升力.

由图2可知，由图可知，三旋翼飞行器在x、y、z轴上的力矩分析如下［5］

2　三旋翼飞行器数学模型的建立

在建立三旋翼无人机的数学模型之前，必须求出适合三旋翼飞行器的坐标转换矩，将物体坐标通过欧拉公式转换为地面坐标［6］

式中:c表示cos；s表示sin.

在建立好坐标转换矩阵后，x、y、z轴3个方向三旋翼无人机受力情况为

根据牛顿第二定律，建立在地面坐标下沿着x、y、z方向的线性方程为

式中K′为空气的阻力系数，空气的阻力和物体运动的速度成正比，再加上飞行器姿态角之间的耦合动量矩又可通过力矩矩阵可得到角加速度的表达式［7］:

式中Ix、Iy、Iz分别为对应轴的转动惯量.

由此得出三旋翼直升机最终动力学数学模型方程为

由于飞行器在悬停状态下对于姿态进行调节的过程中，3个通道的角度变化不会太大，因此，项对于系统不会产生太大的影响，可以在计算过程中不考虑这几项的影响，为了保证飞行器在悬停状态时需要监测的状态量为φ、θ、ψ，所以系统的输出矩阵为Y=（φ，θ，ψ）T，在此选择了4个输入量u（1）、u（2）、u（3）、u（4），这4个输入量的表达式为

由于l′1、l′2、l′3、l1、l2、l3由机体的机械结构决定，为常量，因此可知，系统的输入量由电机3个旋叶的转速所决定，从而建立起数学模型.

3　自抗扰姿态控制器的设计

自抗扰控制器是一种不用依赖精确的数学模型而通过局部误差来抑制全局误差的较为先进的控制方法，具有算法简便、鲁棒性好、抗噪声性能好等优点.常见的自抗扰控制器分为非线性跟踪微分器（tracking differentiator，TD）、扩张状态观测器（extended state observer，ESO）和非线性误差反馈控制模块（nonlinear state error feedback，NLSEF）3个模块［8］.跟踪微分器TD能够跟踪参考输入信号υ（t），安排预期过渡过程，还能够于有限时间单调地跟上输入信号，同时也给出过程的微分信号，用TD来安排过渡过程，是否预先得知目标υ（t）的变化，更重要的是能否实时得到信号υ（t）的值使得系统输的超调减少，TD的输入为υ（t），输出υ1，υ2，…，υn.分别代表经过分步柔化以后的各阶导数.扩张状态观测器ESO能实时估计出作用与系统的扰动总和，并给予补偿的办法替代误差积分的反馈作用.而非线性误差反馈控制模块NLSEF能在非线性领域寻找更合适的组合形式来形成误差反馈律.自抗扰控制器的结构如图3所示.

3.1非线性跟踪微分器的设计

在许多经典意义下的不可微函数作为输入信号用许多传统上的经典方法无法跟踪，但许多在经典意义下不可微的函数却有着其广义函数，对广义函数来说，其微分运算是比较自由的.所以自抗扰控制器引入非线性跟踪微分器环节来构造非线性微分跟踪器.它的设计理论所述为

式（27）所有解都满足

那么对任意局部可积信号υ（t），和任意T＞0，微分方程

的解的第1个分量x1（γ，t），将满足

为了使系统能够更好地跟踪类似阶跃信号的控制量很大的信号，使预期过渡过程能更好地跟踪输入信号，现将f函数定为fhan（x1，x2，γ，h），表示为

式中:h为积分步长；γ为速度因子.选择合适的积分步长和速度因子可以更好地跟踪输入号.

3.2非线性误差反馈设计

由于函数fhan（x1，x2，γ，h）［8］具有快速并消除震颤的特殊功能，因此用它来进行状态反馈的非线性配置，非线性PID和自抗扰控制器等一些中的误差的非线性组合等是很理想的.

为了更有效地把fhan（x1，x2，γ，h）用于状态反馈中，引入阻尼因子c来把fhan（x1，x2，γ，h）中的变量x2改成cx2，得fhan（x1，x2，γ，h）.

在上述公式当中，c、γ、h1是可以调节的参数，c的有限调节可以减小震荡［9］，抑制超调，γ、h1的调节与非线性跟踪微分器的方法相同.

3.3扩张状态观测器设计

对于动态过程而言，系统外部变量的观测来确定系统内部状态变量的装置叫做状态观测器，非线性状态观测器是可以推广到任意阶系统上［8］，如对系统:

可以建立如下状态观测器

在进行数值仿真时，为了避免高频颤振现象的出现，把函数|e1|αsign（e1）改造成原点附近具有线性段的连续的幂次函数

最后，使用基于fal函数的观测器方程组

式中:β01、β02、β03为可选参数；α越小，跟踪越快［10］，但是会影响观测器滤波的效率，本文依据每个模块的整定方法，整定出一组合适的参数.

4　三旋翼飞行器的控制模拟仿真

在上述建模过程中，将三旋翼三通道耦合系统通过数学变换变成了四通道单输入输出系统，更方便用经典的PID控制方法和自抗扰控制方法对系统进行控制调节.

通过三维仿真软件可测得该设计机体的转动惯量和质量分别为

三旋翼自抗扰控制器的设计思路如图4所示.

本文采用Matlab进行对比实验（见图5～16），在各个姿态角上对跟踪，3°、10°、30°阶跃信号的PID控制与自抗扰控制仿真结果进行对比，并且在以上跟踪30°阶跃信号的参数上对于偏航30°进行白噪声干扰和俯仰通道跟踪正弦信号和方波信号的实验，各个参数的值见表1～3（各姿态角参数）.

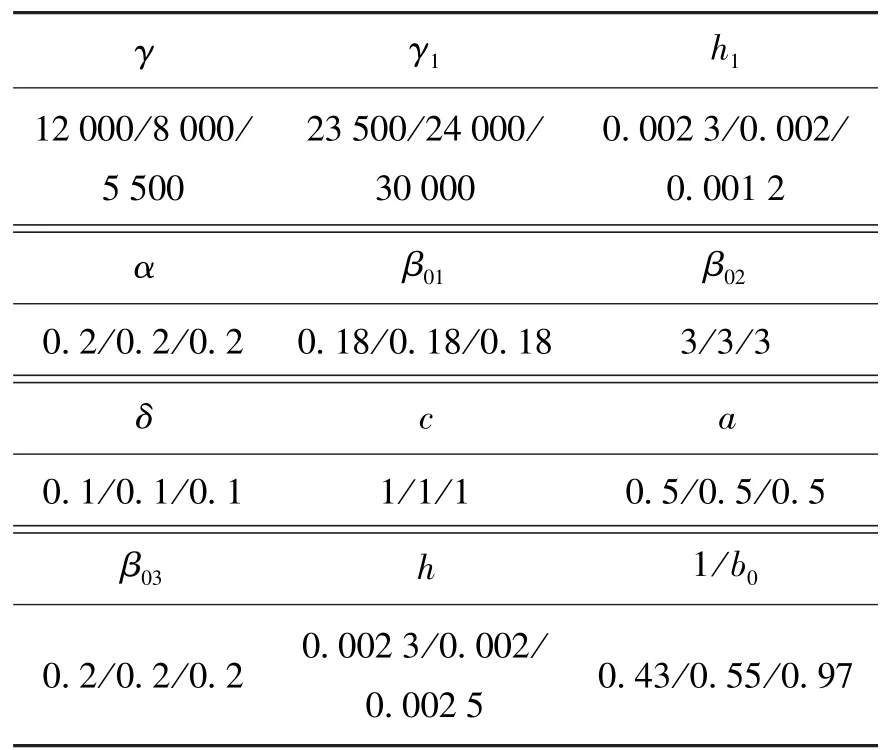
表1　10°姿态角自抗扰参数Table 1 10°attitude angle ADRC parameters

仿真结果表明:在各个单通道姿态角上的不同角度的阶跃信号的响应，自抗扰控制算法超调量要比PID控制算法小，并且响应速度比PID控制算法要迅速.而对于较小的角度的阶跃响应，采用较大的速度因子γ、γ1会使得系统的超调量增大或使系统的曲线不平滑以及欠补偿等一系列不稳定的现象，所以，选择合适的步长h，合适的速度因子γ、γ1来跟踪不同数值的角度阶跃信号，在跟踪30°阶跃信号的参数下进行白噪声实验和跟踪正弦信号和方波信号的实验中，可以看到自抗扰控制方法相比于PID控制方法具有更好地抗干扰和跟踪信号的能力，由此可以充分地体现自抗扰控制的有效性和抗干扰性.

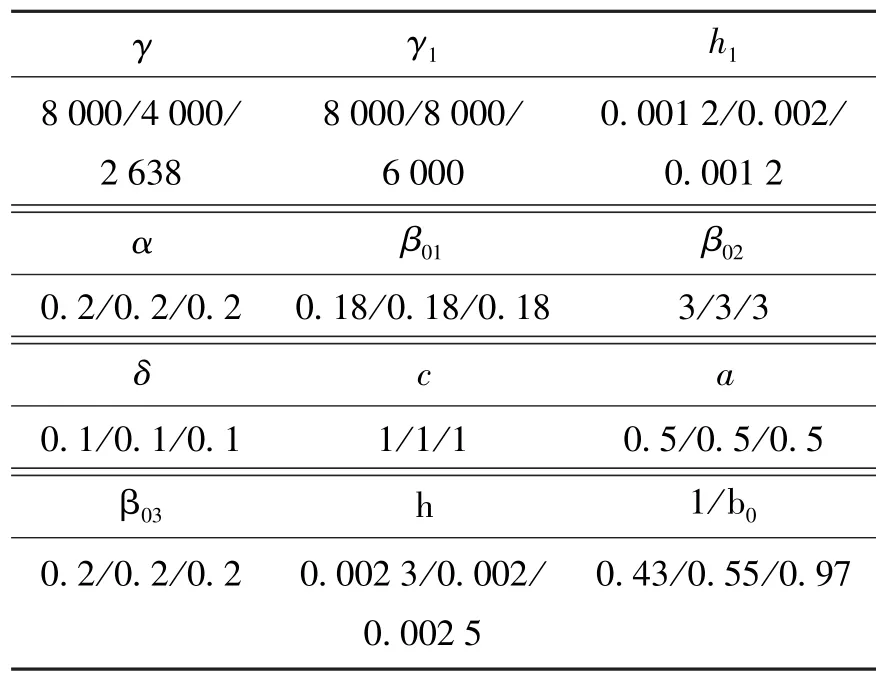
表2　3°姿态角自抗扰参数Table 2 3°attitude angle ADRC parameters

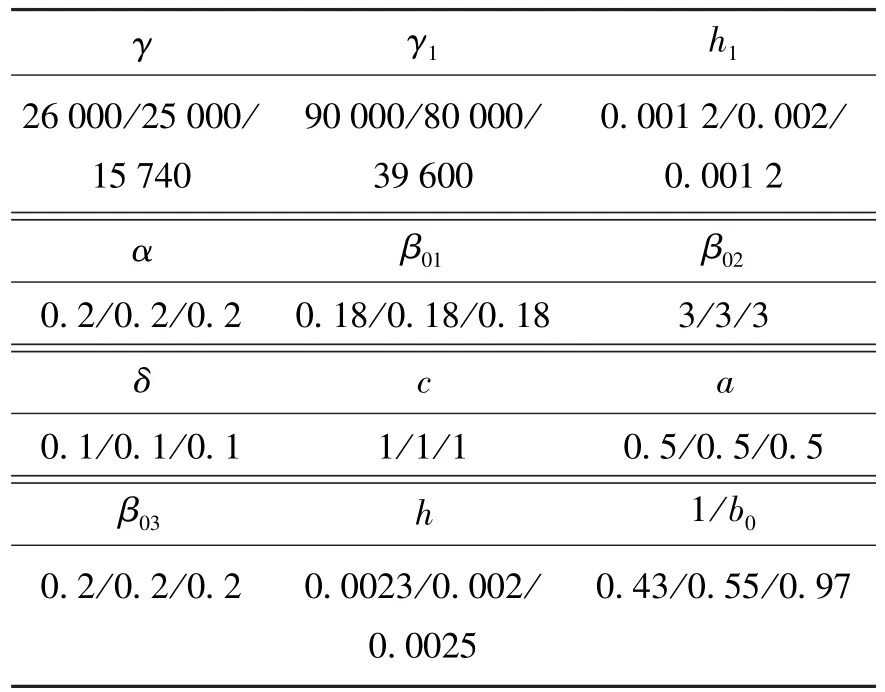
表3　30°姿态角自抗扰参数Table 3 30°attitude angle ADRC parameters

5　结论

1）相比于传统的PID控制方法，自抗扰控制方法具有更好的跟踪阶跃信号的优势.

2）在此基础上，针对于不同幅值的阶跃信号可采取不同的参数进行跟踪.

3）在白噪声的抗干扰实验中，自抗扰控制方法比PID控制方法具有更好的抗噪声效率.

4）在三旋翼动力学模型的基础上，自抗扰控制方法跟踪不同种类的信号比PID控制方法效果更好.

［1］赵晓辉，国倩倩.微型四旋翼飞行器控制系统设计及控制方法研究［D］.长春:吉林大学，2013.ZHAO X H，GUO Q Q.Study on design and control method for mini-quadrotor UAV control system［D］.Changchun:Jilin University，2013.（in Chinese）

［2］杨阳，崔金峰.三旋翼飞行器动力学分析及建模［J］.光学精密工程，2013，21（7）:1-3.YANG Y，CUI J F.Dynamical analysis and mathematical modelingoftricopter［J］.OpticsandPrecision Engineering，2013，21（7）:1-3.（in Chinese）

［3］KENDOUIF S S.Real-time stabilization of a small threerotor aircraft［J］.Aerospace and Electronic Systems，2008，44（2）:3-7.

［4］KENDOUIF S S.Real-time control of a small-scale helicopter having and three rotors［C］//International Conference on Intelligent Robots and Systems.Beijing: IROS，2006:2921-2929.

［5］KENDOUIF S S C.Stabilization and nonlinear control for a noveltri-rotormini-air-craft［C］//Proceedingsof InternationalConferenceonRobotandAutomation.Barcelone:IEEE，2005:2612-2617.

［6］DANG T Q，BUSHNELL P R.Aero dynamics of cross-flow fans and their application to aircraft propulsion and flow control［J］.Aerospace Sciences，2009（45）:1-29.

［7］陈航科，张东升，盛晓超，等.四旋翼飞行器悬停状态姿态控制建模与仿真［J］.计算机仿真，2013，30（11）:41-42.CHEN H K，ZHANG D S，SHENG X C，et al.Modeling and attitude control simulation for four rotor aircraft in hover［J］.Computer Simulation，2013，30（11）:41-42.（in Chinese）

［8］韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008:489-524.

［9］万晖.自抗扰控制器的绝对稳定性分析［J］.上海电力学院学报，2011，27（5）:507-511.WAN H.Absolute stability analysis of active disturbance rejection controller［J］.Journal of Shanghai University of Electric Power，2011，27（5）:507-511.（in Chinese）

［10］韩京清.从PID技术到“自抗扰控制”技术［J］.控制工程，2002，9（3）:13-18.HAN J Q.From PID technique to active disturbances rejection control technique［J］.Control Engineering of China，2002，9（3）:13-18.（in Chinese）

（责任编辑 杨开英）

Modeling of Three-rotor Aircraft and Its Attitude Based on ADRC

RUAN Xiaogang，ZHANG Xiaorui，WANG Danyang
（School of Electronic Information and Control Engineering，Beijing University of Technology，Beijing 100124，China）

According to the status of rotorcraft and mechanical structure of three-rotor，this paper analyzed the torque of a three-rotor aircraft and established its mathematical model.Active disturbance rejection control（ADRC）was applied to the control of attitude.To investigate the performance between ADRC and PID，series of comparative experiments were carried out.Results show that different sizes of step signal can be adjusted by different parameters in ADRC，and ADRC is more effective and rapid than PID.ADRC can not only keep the general framework and structure of PID，but also has better performance on filtering and robustness，which has important guiding significance in engineering and experiments.

three-rotor aircraft；mathematical model；active disturbance rejection control（ADRC）；robustness

U 461；TP 308

A

0254-0037（2016）10-1461-07

10.11936/bjutxb2015020006

2015-02-03

国家自然科学基金资助项目（61375086）；国家“973”计划资助项目（2012CB720000）

阮晓钢（1958—），男，教授，博士生导师，主要从事人工智能与机器学习方面的研究，E-mail:adrxg@bjut.edu.cn