液力变矩器的流量和扭矩的实时监测
2016-10-17刘振杰李翠芬李志伟
刘振杰, 衣 超, 徐 飞, 李翠芬, 李志伟
(中国北方车辆研究所,北京 100072)
液力变矩器的流量和扭矩的实时监测
刘振杰,衣超,徐飞,李翠芬,李志伟
(中国北方车辆研究所,北京 100072)
车辆起步和换挡过程中液力变矩器涡轮扭矩变化对其舒适性有较大影响.为了在控制模型中精确地计算液力变矩器涡轮的扭矩,以搭载W305型液力变矩器的某轻型越野车为例,根据液力变矩器动态特性方程,搭建了液力变矩器仿真模型,并将液力变矩器的外特性仿真曲线与试验获取的外特性曲线进行了对比,误差小于3%,表明建立的液力变矩器的仿真模型满足滑模观测器的要求.采集试验车发动机转速(即泵轮转速)和输入轴转速(即涡轮转速),建立滑模观测器,观测涡轮扭矩和液力变矩器流量.结果表明,使用滑模观测器能准确地计算液力变矩器涡轮扭矩和流量.该滑模观测器已应用于车辆起步和换挡过程中液力变矩器的控制.
液力变矩器;涡轮扭矩;滑模观测器
在车辆起步及换挡过程中,液力变矩器的泵轮、涡轮转速和扭矩变化较大,这对有液力变矩器控制的车辆舒适性有非常大的影响,因此研究液力变矩器的动态特性[1]具有非常重要的意义.传统的基于计算流体力学流场分析的全流道瞬态流场分析虽然考虑了液力变矩器的动态特性[2-4],但其分析是基于时间的瞬态流场扭矩预测,无法考虑发动机扭矩及车辆负载的影响.为此,Hrovat和Tobler提出了基于四个一阶微分方程的液力变矩器动态特性描述方程[5],该方程是以泵轮扭矩、涡轮扭矩为输入条件,分析液力变矩器动态特性.
车辆液力变矩器的控制是以涡轮扭矩为控制目标,但是液力变矩器的泵轮转速、扭矩和涡轮转速是可以获取的,而涡轮扭矩是未知的.解决现有问题的主要办法是在控制模型中建立液力变矩器扭矩计算模型[6],但是现有扭矩计算模型均是基于液力变矩器的稳态特性建立的,不能体现液力变矩器工作时的实际扭矩变化.为此,本研究以搭载了W305型液力变矩器的某轻型越野车为例,搭建了液力变矩器动态模型,建立了滑模观测器来计算液力变矩器涡轮的扭矩,并将其应用于该车的液力变矩器的控制中.
1 液力变矩器仿真模型
1.1液力变矩器动态特性描述
从整个动力传动系统建模及控制的角度出发,需要一个完整的描述液力变矩器动态特性的模型,该模型可以用来做以下研究:
1)液力变矩器设计参数的改变对液力变矩器性能的影响;
2)当发动机节气门开度突变或液力变矩器涡轮、泵轮速比突变时,液力变矩器的瞬态特性变化;
3)发动机扭矩脉冲特性的改变对液力变矩器振动冲击的影响.
液力变矩器的动态特性可以用液力变矩器泵轮、涡轮、导轮的动量守恒方程(1)~(3)以及液力变矩器的能量守恒方程(4)来描述.

(1)

(2)
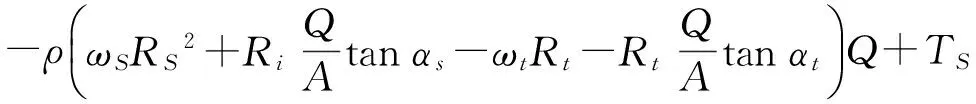
(3)
(4)
能量守恒方程(4)中的PL为液力变矩器的能量损失,包括冲击损失和压力损失,即:
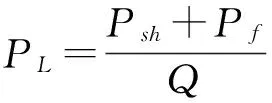
(5)
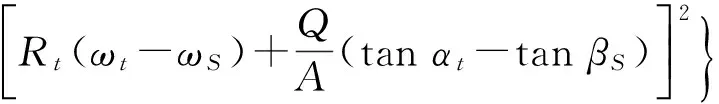
(6)
(3+tan2αi+tan2αt+tan2αS).
(7)
式中:ρ为液力变矩器工作油密度,kg/m3;A为工作油循环圆截面积,m2;Ri为泵轮半径,m;Rt为涡轮半径,m;Rs为导轮半径,m;αi为泵轮出口角,(°);αt为涡轮出口角,(°);αs为导轮出口角,(°);βi为泵轮入口角,(°);βt为涡轮入口角,(°);βs为导轮入口角,(°);Ii为泵轮转动惯量,kg·m2;It为涡轮转动惯量,kg·m2;Is为导轮转动惯量,kg·m2;Lf为流体惯性长度,m;Csh为流体冲击损失系数;Cf为流体摩擦损失系数;Si为泵轮设计常数;St为涡轮设计常数;Ss为导轮设计常数.
以上参数均来源于W305型液力变矩器设计参数.导轮扭矩Ts作为一个切换准则,在整个液力变矩器工作范围内,当液力变矩器工作在偶合器工况之前,导轮是固定的,导轮转速ωs设定为零;当液力变矩器工作在偶合器工况时,导轮自由旋转,此时导轮扭矩Ts设定为零.
这种方法用来解决前面提出的描述液力变矩器的4个一阶微分方程.当液力变矩器工作在偶合器工况之前,导轮转速ωs设定为零,此时上述方程变为3个一阶微分方程和1个代数方程.当Ts达到设定的阀值时认为液力变矩器达到偶合器工况,设定的阀值为0.1 N·m.当达到偶合器工况时,用上述一阶4个微分方程来描述液力变矩器的特性.
1.2液力变矩器动态仿真模型验证
Hrovat和Tobler提出的液力变矩器动态特性描述方程是以泵轮扭矩、涡轮扭矩为输入条件,分析液力变矩器动态特性.在MATLAB/Simulink环境中搭建W305型液力变矩器动态仿真模型,仿真模型结构如图1所示.

图1 液力变矩器仿真模型结构图
根据状态方程,模型共分为4个模块.泵轮模块以导轮转速、流量、流量变化率、泵轮扭矩为输入,以泵轮转速、泵轮转速变化率为输出;涡轮模块以泵轮转速、流量、流量变化率、涡轮扭矩为输入,以涡轮转速、涡轮转速变化率为输出;导轮模块以涡轮转速、流量、流量变化率、导轮扭矩为输入,以导轮转速、导轮转速变化率为输出.流量模块以泵轮转速、泵轮转速变化率、涡轮转速、涡轮转速变化率、导轮转速、导轮转速变化率为输入,以流量、流量变化率为输出.
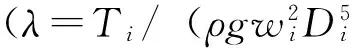
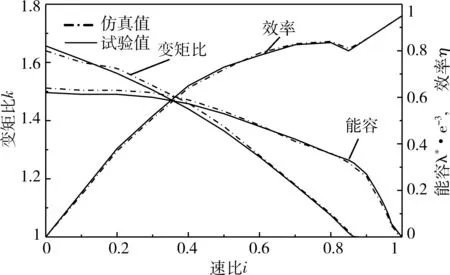
图2 液力变矩器外特性曲线
由图2可以看出,液力变矩器的变矩比、效率、能容仿真曲线和试验曲线也具有很好的一致性,误差在3%以内,说明液力变矩器的动态模型是准确可靠的,从而为下一步涡轮扭矩计算奠定了良好的基础.
2 液力变矩器的流量和涡轮扭矩的动态计算
液力变矩器涡轮扭矩计算流程如图3所示.

图3 液力变矩器涡轮扭矩计算流程图
首先采集某轻型越野车的发动机转速(即泵轮转速)和涡轮转速信息,通过基于液力变矩器动态特性方程建立的滑模观测器计算其扭矩,将计算扭矩输入到液力变矩器动态仿真模型中进行对比验证.
2.1滑模观测器搭建
在现有的试验和仿真技术条件下,液力变矩器导轮转速和扭矩难以获取,通常对其进行假设.在变矩器工况时,导轮转速设定为零;在偶合器工况时,导轮转速设定与涡轮转速相同,这种假设虽不能与实际情况相符,但不影响其仿真结果.由公式(4)可知,液力变矩器流量Q仅与泵轮转速ωi、涡轮转速ωt以及导轮转速ωs有关,这样关于液力变矩器的4个一阶微分方程(1)~(4)中,仅式(1)、式(2)起主要作用,式(1)、式(2)简化成式(8).

(8)
式(8)中的Ti、Tt作为带计算的扭矩输入.如果一个线性系统是可观测的,那么其任何初始状态是可重构的.但对于非线性系统来说,其输入对其是否可观测具有重大影响.
非线性系统的计算误差定义为:
(9)
那么含未知输入非线性系统的滑模观测器为:
(10)
式中:v1=M1sgn(e1),v2=M2sgn(e2).
假设非线性系统至少有部分输入已知,且未知输入是有界的,那么M定义如下:
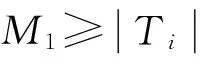

(11)
式(8)中的Ti、Tt被不连续的向量vi、v2取代,那么明显地可以发现,动态误差的表达式如式(12)所示.


(12)
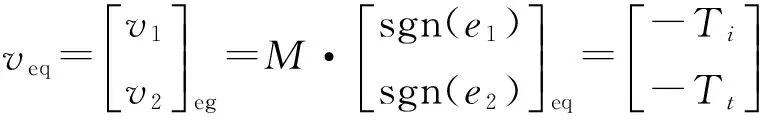
(13)
式中:veq为等效输出误差,代表不连续向量v1、v2的平均特性.
2.2预测结果
采用台架试验的方法验证滑模观测器的可行性.以某轻型越野车为试验车,该车为前置前驱.将该车前轮悬置,后轮做好固定后,通过CAN总线采集全油门开度下的泵轮、涡轮转速值.仿真时间为2.5 s,变速箱始终处于1挡.其仿真结果如图4、图5、图6所示.通过对比仿真模型与滑模观测器模型数据的一致性来验证滑模观测器模型的准确性.
图4为仿真模型与滑模观测器模型关于液力变矩器流量的对比曲线图.
由图4可知,从起步开始到0.5 s左右时,液力变矩器流量发生剧烈变化,原因为发动机转速、扭矩迅速增大且发动机转速处于不稳定状态,此时液力变矩器的流量也会随之产生不稳定的供给;液力变矩器的流量随着时间先迅速增加,随后慢慢减小,最终趋于平衡,随着转速增大,泵轮涡轮转速差慢慢减小,液力变矩器的变矩功能也会慢慢减小,直至到达偶合器工况时,液力变矩器不再具有变矩功能,流量趋于平衡.仿真结果与滑模观测器结果具有很好的一致性,说明所设计的滑模观测器是可行且有效的.

图4 液力变矩器流量图
图5为液力变矩器泵轮和涡轮的转速的仿真值与滑模观测器计算值的对比曲线图.
由图5可知,泵轮转速的仿真值与滑模观测器计算值大体相同,涡轮转速仿真值与滑模观测器计算值趋势相同;从起步开始到0.5 s这个阶段发动机转速波动大,而涡轮计算值更能说明液力变矩器工作的不稳定性;从0.5到1.8 s左右,涡轮转速计算值比仿真值略低,但转速变化率高,更好地解释了液力变矩器在此阶段的变矩功能;从1.8到2.5 s涡轮转速计算值与仿真值大体相同,说明基于滑模观测器的涡轮转速计算值比仿真值更能反映车辆起步特性.

图5 液力变矩器转速图
图6为基于滑模观测器的液力变矩器泵轮、涡轮动态扭矩曲线图.

图6 液力变矩器泵轮、涡轮动态扭矩图
图6中,泵轮扭矩为发动机实际输出扭矩,涡轮扭矩为基于滑模观测器的计算扭矩,该图为车辆起步工况液力变矩器泵轮、涡轮的动态扭矩特性.
由图6可以看出,从起步开始到0.5 s这个阶段,液力变矩器处于不稳定工作状态时,涡轮扭矩变化剧烈,这与车辆起步实际状况是相符的;随后,涡轮扭矩逐渐减小,直到到达偶合器工况,液力变矩器失去变矩作用.该结果验证了基于滑模观测器的涡轮扭矩计算模型的准确性.
3 结 论
针对现有的基于台架试验以及流体仿真的液力变矩器动态特性的预测结果不能很好地反映液力变矩器涡轮扭矩瞬态变化特性这一问题,根据Hrovat和Tobler提出的液力变矩器动态特性描述方程,建立了W305型液力变矩器仿真模型,其液力变矩器的外特性仿真曲线与台架试验曲线的误差小于3%,表明建立的液力变矩器仿真模型精度较高,满足建立滑模观测器要求;针对车辆液力变矩器的
控制以涡轮扭矩为控制目标,但是涡轮扭矩又未知这一问题,建立了滑模观测器.以搭载W305型液力变矩器的某越野车为例,模拟车辆起步时,计算液力变矩器的特性,结果表明,使用滑模观测器计算的液力变矩器的流量,与液力变矩器仿真模型计算一致;涡轮扭矩变化与实际车辆特性相符,满足车辆液力变矩器的控制要求.该滑模观测器已应用于该车起步和换挡过程中液力变矩器的控制.
[1]Kotwicki. A.Dynamic Models for Torque Converter Equipped Vehicles[C].//SAE Technical Paper, 820393,1982.
[2]陈东升,项昌乐,刘辉. 液力变矩器的动态特性和动力学模型研究[J]. 中国机械工程,2002,13(11):913-917.
[3]李吉元,闫清东. 新型牵引-制动型液力变矩器动态特性研究[J]. 系统仿真学报,2005,17(10):2521-2525.
[4]刘春宝,马文星,朱喜林. 液力变矩器三维瞬态流场计算[J]. 机械工程学报,2010,46(14):161-166.
[5]Hrovat. Dand Tobler. W. E.Bond Graph Modeling and Computer Simulation of Automotive Torque Converters [J]. Journal of the Franklin Institute, 1985, 319(1/2):93-114.
[6]Rong. W. H, Tanaka. K and Tsukamoto. H. Torque Converter with Lock-up Clutch by Bond Graphs[C].//ASME, FEDSM97-3368SM97, 2007.
Real-time Monitoring Flow and Torque of TorqueConverter Clutch
LIU Zhen-jie,YI Chao,XU Fei,LI Cui-fen,LI Zhi-wei
(China North Vehicle Research Institute,Beijing 100072,China)
Vehicles riding comfort was affected by turbine torque changes of Torque Converter Clutch in the process of starting and shifting conditions. Taking an off-road vehicle that installed the W305 Torque Converter as an example, in order to calculate the turbine torque precisely, a Torque Converter Simulink model was established. Simulation results and experimental results were compared, and the error was within 3%. Pump speed(equal to engine speed) and turbine speed were obtained in real time through the establishment of a sliding mode observer, and the turbine torque as well as the flow of Torque Converter were monitored. The results showed that the turbine torque and the flow of Torque Converter were calculated accurately by using the sliding mode observer.
rorque converter;turbine torque;sliding mode observer.
1009-4687(2016)03-0008-05
2016-05-05.
刘振杰(1986-),男,工程师,研究方向为传动信息与控制.
U463.22+1
A
