永磁同步电机混合多模型控制方法研究

姚统，张华强，鲁晓彤

（哈尔滨工业大学（威海）电气工程系，山东 威海 264209）

永磁同步电机混合多模型控制方法研究

姚统，张华强，鲁晓彤

（哈尔滨工业大学（威海）电气工程系，山东 威海 264209）

以面贴式三相永磁同步电机（PMSM）为研究对象，研究基于递推最小二乘法和模型参考自适应法的混合多模型在线辨识方案，通过指标函数实时优化动态模型库。在电机运行过程中，根据“优胜、劣汰”规则匹配调节器模型和参数，提出基于混合多模型控制的永磁同步电机在线控制策略，达到在线整定参数的目的。将混合多模型策略应用于PMSM调速系统测试平台，仿真和试验结果验证了所提方案的可行性和混合多模型控制策略的正确性。

永磁同步电机；递推最小二乘法；模型参考自适应法；混合多模型；在线辨识

基于传统的PI调节器设计与电机的参数有关，因此参数的准确性决定控制器的性能。由于生产工艺的变化或负载特性的不确定性，系统在运行中参数可能发生变化，为保证动态性能，提高稳定性和鲁棒性，就需要研究多模型控制技术。

1975年提出的多模型控制技术，没有采用切换方法，而是采用加权平均算法，提高控制器输出的鲁棒性。后来美国Narendra教授及其团队研究的多模型切换技术，采用指标函数选择切换模型，开创了多模型切换技术的先河［1-3］。针对非线性系统参数的不确定性，学者Cezayirli等采用多模型切换控制方法提高系统的动态响应［4］。文献［5-6］将多模型切换控制与神经网络学习进行联合，应用到非线性系统中。

多模型切换控制关键技术之一就是建立模型库，模型库中的模型与实际系统匹配程度决定了模型库的优劣。由于被控系统的不确定性，需要大量的模型来匹配关键工作点。模型库模型数量越多匹配性能就越好，但计算量大；模型数量太少又不能很好匹配实际系统，动态响应变差。为保证匹配度、减少计算量，文献［7-8］对模型库进行优化，在相同的模型数量下，提高了匹配度，但模型数量仍然较大。文献［9］提出在线学习的动态模型库优化方法，实时在线优化模型库中的模型，使模型向实际系统趋近，保证匹配度。

近年来，多模型控制技术在BTT导弹系统、汽车温度调节系统、磁悬浮系统、飞行器控制系统等方面得到良好应用［10-14］。PMSM调速系统对调速性能要求苛刻，而电机参数易受温度等因素影响，具有不确定性，因此本文主要研究基于混合多模型及其切换控制技术的永磁同步电机调速控制系统。

1　基于RLSE的多模型控制

1.1多模型系统建立

为了应对电机参数的变化，采用RLSE在线实时辨识电机参数，得到离散模型的参数向量。因辨识结果易受干扰，若只辨识和保存1组参数向量，可能会偏离真实值。因此需要辨识多组参数向量历史值，保存误差小的参数向量，误差大的参数向量自然剔除，以提高参数辨识的鲁棒性，为控制器模型提供准确的电机参数。

电机初次运行，需要1组离线辨识参数向量作为控制器基本参数。所以多模型系统中的模型由1个固定参数模型和1个可变参数模型库组成，可变参数模型库由基于RLSE辨识得到的多个模型组成。若模型过多计算量大，模型太少鲁棒性会变差，因此限定模型为3个。基于RLSE的多模型控制系统结构如图1所示。

图1　基于RLSE的多模型控制系统结构Fig.1　Structure of multi model control system based on RLSE

由RLSE优化的模型库如下：

从表2可以看出，从1级到3级，土壤 pH 降低，酸性越来越强，水田中作物所需氮养分呈上升趋势，磷养分下降。从 4 级到 6 级，氮含量逐渐减少，磷养分逐渐上升；从1级到6级，旱田土壤中钾养分大幅度减少，硼养分递增，锌含量整体呈递减趋势。在水田中，有机质在各级别土壤中的含量差别不大，但在旱田中整体呈减少趋势[7]。

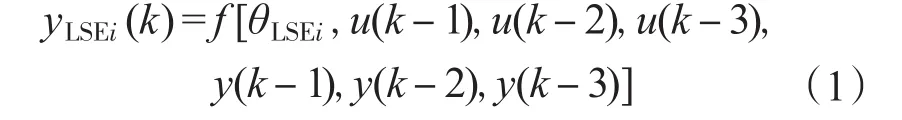
式中：yLSEi（k）为模型i的预测输出；θLSEi为模型i的参数向量。

当前实际输出与预测输出误差为

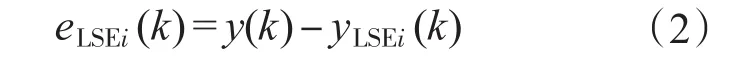
式中：y（k）为k时刻系统输出的检测值。

模型i在有限时域长度h内预测误差，设模型i的指标函数为

式中：α为当前误差权重，α≥0；β为历史误差权重，β＞0；τ为遗忘因子，τ＞0；i为模型的标号，i∈｛1，2，3｝。

由RLSE辨识得到的3个模型采用“劣汰”方法优化，用指标PLSEi（k）最大的模型参数向量θLSEi替换为当前辨识的θLSE（k），即：

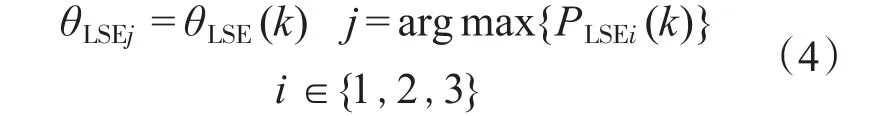
式中：θLSEj为模型j的参数向量；θLSE（k）为当前RLSE辨识的参数向量。

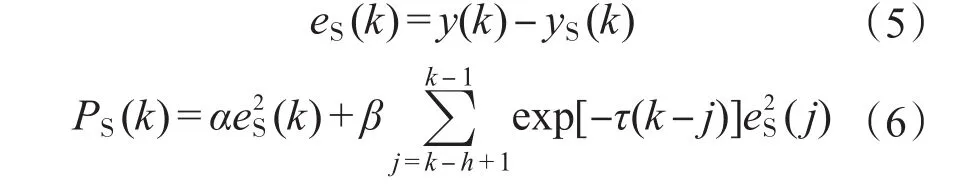
4个PMSM离散模型对应4个指标值，分别为PS，PLSE1，PLSE2，PLSE3，选择最小值对应的模型为最优模型，以此模型的参数向量作为控制器参数在线整定依据，称之为“优胜”。

1.2多模型控制系统仿真

仿真时，对4个模型编号，固定模型编号为1，RLSE模型编号为2，3，4。仿真系统主要参数配置如表1所示。

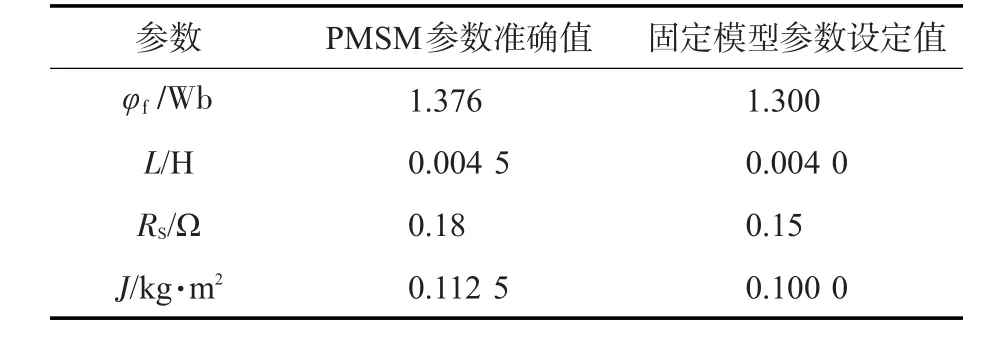
表1　仿真系统的主要参数配置Tab.1　Main parameters configuration of simulation

基于RLSE的多模型控制系统转速仿真结果如图2所示，多模型控制器采用“劣汰”方法在线优化模型参数，采用“优胜”方法挑选最佳匹配模型作为PMSM的PI调节器参数设计依据。图2 中Number为挑选出的最佳匹配模型编号，开始时，基于RLSE的辨识过程未稳定，辨识参数处于有效优化阶段，PI调节器参数随之变化。待RLSE辨识稳定后，匹配的参考模型号不再变化，PI调节器参数基本稳定不变，转速很快稳定下来，结果表明基于RLSE辨识的多模型切换可以保证系统的稳定运行。

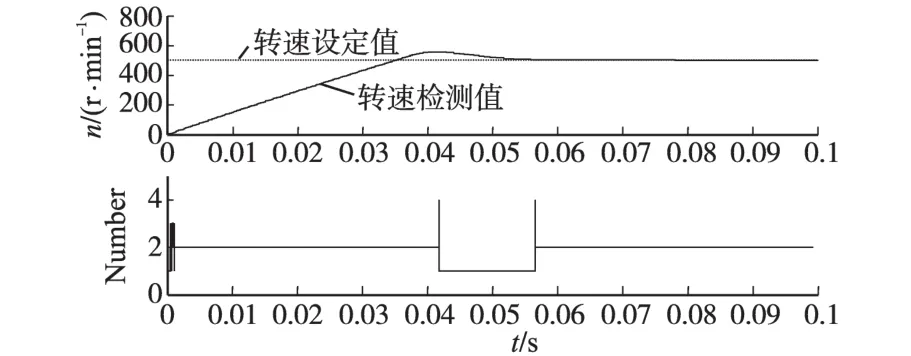
图2　基于RLSE的多模型控制系统转速仿真结果Fig.2　Simulation results of multi model control system based on RLSE

2　基于MRAS的混合多模型控制

2.1混合多模型系统建立

在一定误差范围内，基于RLSE辨识速度较快，而基于MRAS辨识较慢，但基于MRAS辨识误差较小。因此提出混合多模型控制，系统中含有2种可变模型库：一个是基于RLSE辨识的模型库；另一个是基于MRAS辨识的模型库，还有一个固定模型，供不同的工作点择优选用。由不同辨识方法获得的参数值构建的模型越接近实际模型越好。考虑到计算量和鲁棒性因素，限定每个模型库中含有3个可变模型，于是系统共有7个模型，结构如图3所示。

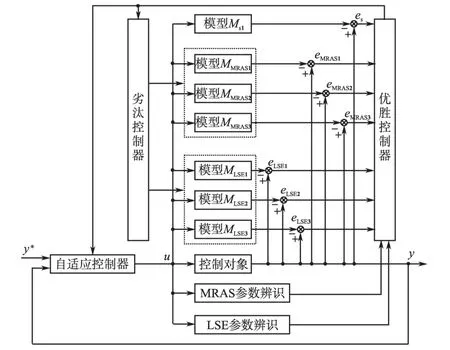
图3　混合多模型控制系统结构Fig.3　Hybrid multi model control system structure

2.2混合多模型的切换策略

多模型切换控制是通过选择一个合适模型来调节控制器参数，改变其结构和性能，达到匹配控制系统的目的。采用“优胜”方法选择模型，用指标P（k）最小的模型中参数向量θ（k）作为调整控制器的依据，将7个模型分别编号为M1～M7，其对应的指标函数为 P1（k）～P7（k）。同时引入滞环方法，防止模型频繁切换，切换策略如下：

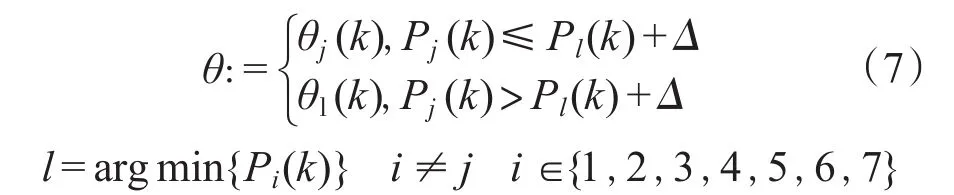
式中：θ为控制器调整时使用的参数向量；当前控制器采用第j个模型；Δ为滞环宽度，Δ＞0。

2.3混合多模型控制系统仿真

仿真时，对7个模型进行编号，固定模型编号为1，基于RLSE的模型编号为2，3，4，基于MRAS的模型编号为5，6，7。仿真系统的主要配置参数同样如表1所示。

仿真结果如图4所示，多模型控制器采用“劣汰”方法在线优化多模型参数，采用“优胜”方法选择最佳匹配模型作为PMSM的PI调节器参数整定依据，图中Number为挑选出最佳匹配模型编号。开始RLSE辨识的模型和固定模型被选择的概率较大，然后倾向于MRAS辨识的模型，模型参数处于有效优化过程，待RLSE和MRAS辨识稳定后。由于MRAS辨识的稳态精度比RLSE辨识高，所以最终选定的参考模型来自MRAS辨识的模型库。结果表明，基于混合多模型控制的切换模式能够保证系统的稳定运行，综合了RLSE辨识的快速性和MRAS辨识的高稳态精度等特性。

图4　混合多模型控制系统转速仿真结果Fig.4　Simulation results of hybrid multi model control system

3　PMSM混合多模型控制实验研究

永磁同步电机调速系统采用380 V/50 Hz三相交流电源，利用变频装置驱动电机运行，负载为三相永磁同步发电机。测试平台还有力矩传感器、示波器、PC机、仿真器等辅助调试设备。系统结构如图5所示。

图5中，Emulator为TI公司出品的DSP仿真器，型号为XDS100V2；Torque Transducer为力矩传感器；Encoder为2 500线增量式正交编码器；Load为Y型连接的纯电阻负载；Rectifier，Inverter和DSP Board共同组成变频驱动装置。由供电箱、15 kW变频器、PMSM、力矩传感器、示波器、DSP仿真器和PC机组成的永磁同步电机变频测试平台。

试验电机参数为：额定功率PN=0.4 kW，额定转速nN=3 000 r/min，额定电流IN=2.8 A，额定电压UN=220 V，极对数p=4，交轴电感Lq=6 mH，直轴电感Ld=6 mH，定子相电阻Rs=1.37Ω，转子磁链Ψf=0.037 8 Wb，转动惯量J=3.221×10-5kg·m2，载波频率fc=10 kHz，直流母线电压UDC=580 V。

进行调试，变频器硬件电路有2路独立的模拟量输出模块，输出电压范围0～10 V，输出电压控制2路PWM占空比。试验中，将所有信号进行归一化处理，改变PWM占空比，输出电压同步改变，达到监测变量的目的。得到的uα和uβ波形如图6所示，uα和uβ均为正弦波，而且uα相位比uβ超前90°。

图5　永磁同步电机调速系统结构Fig.5　Structure of permanent magnet synchronous motor speed control system

图6　uα和uβ波形Fig.6　uαanduβwaveforms

在PMSM双闭环控制的基础上，引入多模型切换控制，在线整定PI调节器参数，系统结构如图7所示，PI Para Adjust模块采用基于混合多模型库的PI参数在线调整方法，试验给定转速500 r/min，对应电角度频率33.33 Hz。转子位置和U相电流波形如图8所示，U，V两相电流波形如图9所示。可以看出，位置信号频率33.33 Hz， U，V两相电流波形为正弦波，说明混合多模型控制效果较好。

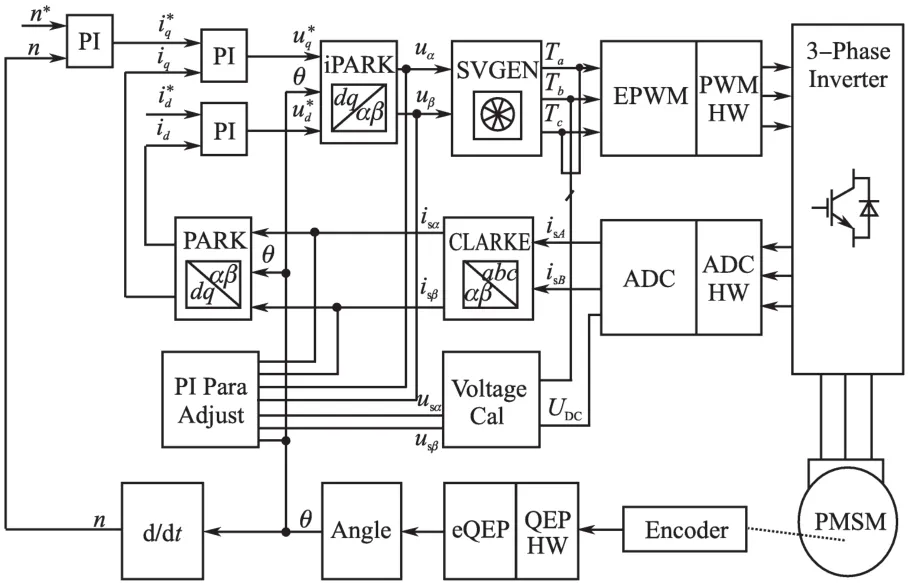
图7　基于转子磁场定向的永磁同步电机双闭环矢量控制系统Fig.7　Double closed-loop vector control system of PMSM based on rotor flux orientation

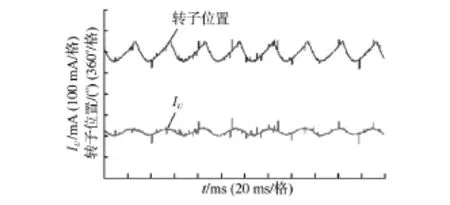
图8　转子位置和U相电流波形Fig.8　Rotor position and U phase current waveforms

图9　U，V两相电流波形Fig.9　V phase and U phase current waveforms

4　结论

本文以三相PMSM为研究对象，提出混合多模型控制策略，研究了基于混合多模型控制的PMSM驱动系统，提出了由基于RLSE辨识的模型库和固定模型组成的多模型控制系统，以及由基于MRAS辨识的模型库和固定模型组成的多模型控制系统。遵循“优胜、劣汰”原则，综合两者优点，选择由2种在线辨识方法建立的模型库和固定模型组成混合多模型控制系统，提高系统的鲁棒性和稳定性。通过Matlab/Simulink仿真验证该方法的可行性。将所提混合多模型控制方法应用于永磁同步电机调速系统，利用变频装置驱动电机运行，负载为三相永磁同步发电机。采用CCS5.2进行变频算法设计，分别对模块和系统进行实验调试，实现了基于混合多模型控制的三相PMSM双闭环矢量控制功能，获得了良好的动态和稳态性能。

［1］Athans M，Castanon D，Dunn K，et al.The Stochastic Control of the F-8C Aircraft Using a Multiple Model Adaptive Control （MMAC）Method-part I：Equilibrium Flight［J］.IEEE Trans⁃actions on Automatic Control，1977，22（5）：768-780.

［2］ Narendra K S，Balakrishnan J.Improving Transient Response of Adaptive Control Systems Using Multiple Models and Switching［J］.IEEE Transactions on Automatic Control，1994，39（9）：186-1866.

［3］Narendra K S，Balakrishnan J.Adaptive Control Using Multi⁃ple Models［J］.IEEE Transactions on Automatic Control，1997，42（2）：171-187.

［4］Narendra K S，CHENG X.Adaptive Control of Discrete-time Systems Using Multiple Models［J］.IEEE Transactions on Au⁃tomatic Control，2000，45（9）：1669-1686.

［5］ 翟军勇，费树岷，达飞鹏.基于神经网络多模型自适应切换控制研究［J］.中国电机工程报.2005，25（24）：61-66.

［6］ Fu Y，Chai T Y.Nonlinear Multivariable Adaptive Control Us⁃ing Multiple Models and Neural Networks［J］.Automatica，2007，43（6）：110-1110.

［7］ Zhivoglyadov P，Midleton R，Fu M.Localization Based Switch⁃ing Adaptive Control for Time-varying Discrete-time Systems ［J］.IEEE Transactions on Automatic Control，2000，45（4）：752-755.

［8］Gustafson J，Maybeck P.Flexible Space Structure Control Via Moving-bank Multiple Model Algorithms［J］.IEEE Transac⁃tions on Aerospace and Electronic Systems，1994，30（3）：750-757.

［9］ 翟军勇，费树岷.基于在线学习的多模型自适应控制［J］.中国电机工程报，2005，25（9）：80-83.

［10］穆向禹，周荻，段广仁.BTT导弹的抖动抑制多模型切换控制［J］.航空学报，2002，23（3）：268-271.

［11］段广仁，王好谦.多模型切换控制及其在BTT导弹设计中的应用［J］.航空学报，2005，26（2）：144-147.

［12］彭辉，高杰.多模型切换控制方法在磁悬浮系统中的应用［J］.控制工程，2011，18（2）：206-209，247.

［13］王宇飞，吴庆宪，姜长生，等.近空间飞行器的多模型切换控制［J］.控制与决策，2012，27（10）：1452-1458.

［14］张华，沈胜强，郭慧彬.多模型分形切换预测控制在主汽温度调节中的应用［J］.电机与控制学报，2014，18（2）：108-114.

Study on Hybrid Multiple Model Control Method for Permanent Magnet Synchronous Motor

YAO Tong，ZHANG Huaqiang，LU Xiaotong
（Department of Electrical Engineering，Harbin Institute of Technology at Weihai，Weihai 264209，Shandong，China）

Taking the stick-type three-phase permanent magnet synchronous motor（PMSM）as the research object，studied the hybrid multiple model online identification scheme based on the recursive least squares estimation （RLSE）method and model reference adaptive system（MRAS）method.Dynamic model library was optimized real-time by index function.A control system based on hybrid multi-mode library was proposed and the parameters were adjusted online according to the rule“superior win，bad discard”.The hybrid multi model strategy was applied to the PMSM speed control system.The simulation and experimental results verify the feasibility and correctness of the proposed scheme.

permanent magnet synchronous motor（PMSM）；recursive least squares estimation（RLSE）method；model reference adaptive system（MRAS）method；hybrid multi-model；online identification

TM343

A

2015-09-10

修改稿日期：2016-02-25

国家自然科学基金（51377168）；科技部创新基金（11C26223702363）

姚统（1988-），男，硕士，工程师，Email：yaotong888@qq.com