基于双参数匹配追踪算法的不同孔深爆炸地震波特性研究

周　辉， 龙　源, 钟明寿， 谢兴博， 郭　涛(解放军理工大学 野战工程学院，南京　210007)



基于双参数匹配追踪算法的不同孔深爆炸地震波特性研究

周辉， 龙源, 钟明寿， 谢兴博， 郭涛(解放军理工大学 野战工程学院，南京210007)

利用爆炸地震波信号的非平稳随机特性，对其进行Hilbert变换转换成复数信号，获得爆炸地震波信号瞬时频率和相位双参数。使用双参数匹配追踪(Matching Pursuits)算法分解爆炸地震波信号，有效提高了匹配追踪(MP)算法的扫描效率，降低算法复杂度，较传统过完备匹配追踪算法运算速率明显提高;结合维格纳瑞利分布(Wigner Ville Distribution,WVD)分析了不同孔深的爆炸地震波时频特性，有效消除了WVD交叉干扰项的影响。分析结果表明：在一定深度范围内，孔深增加，爆炸地震波能量增大，但高频能量衰减更严重；当孔深超过一定深度时，爆炸地震波高频能量衰减趋于稳定。

双参数；匹配追踪；维格纳瑞利分布；孔深；爆炸地震波

爆炸地震波的传播[1-2]受到多种因素的影响，由于介质条件的多变性和边界条件的复杂性，目前尚不能从理论上对包含有爆炸荷载作用下特定介质本构关系的波动方程进行精确求解。因此，对爆炸地震波特性主要通过实验和实际测试进行研究[3-5]。通过对实测数据进行归整和合理剔除后，采用各种理论方法[6-7]在幅域，时域和频域内分析处理数据，得到地震波的特性和基本规律。

MALLAT等[8]提出的匹配追踪算法(Matching Pursuit,MP)是信号稀疏分解最常用的一类算法。其基本思想就是在满足一定条件的情况下，用最少的一类信号原子来表示原信号。该方法有很多优良的性质，如较高的时间—频率分辨率，暂态结构的局部自适应性，信号结构的参数表示更加灵活等[9-10]。其核心思想是将原信号表示为一系列与信号局部结构特征最佳匹配的时频原子的线性组合，然后求各时频原子维格纳瑞利分布(Wigner Ville Distribution,WVD)并将其叠加，得到信号的时频分布，并能很好的降低WVD交叉干扰项的影响[11]。由于子波受振幅、频率、中心时间和相位控制，为了提高匹配追踪算法的扫描效率，本文利用Hilbert变换，将地震信号转换为复数地震信号[12-13]，提前提取地震信号瞬时频率和相位参数信息来确定动态扫描范围，提高了运算效率，取得了较好的效果。

本文拟通过在野外进行的多组不同孔深土中爆炸试验测得的地震波信号，运用双参数匹配追踪算法来分析孔深对爆炸地震波特性的影响。

1　双参数匹配追踪算法的时频分析

1.1匹配追踪算法原理

匹配追踪算法是一种贪婪算法，是将信号在超完备子波库中进行分解，超完备意味着信号的分解目标在信号所组成的空间中足够密集，因此无法保持相互正交的基函数特性，因此信号被分解为子波的线性组合[14]，假设D为进行信号分解的超完备子波库，信号为f，长度为N，D中的元素满足：

D={gγ:γ∈Γ}‖gγ‖=1

匹配追踪算法通过把信号f垂直投影到子波库D的匹配子波上。设gγ0∈D，则f可以表示为：

f=〈f,gγ0〉gγ0+Rf

(1)

式中：Rf为信号f利用匹配子波gγ0进行近似后的差值。为了使差值尽可能小， 就必须使内积项〈f，gγ0〉尽可能大。很显然,gγ0与Rf是正交的，因此：

(2)

设R0f=f，且进行了n次迭代(n》0)得到差值Rnf，此时再选择一个匹配子波gγn∈D，使其匹配Rnf，即

Rnf=〈Rnf,gγn〉gγn+Rn+1f

(3)

Rn+1f就是进行了n+1次迭代得到的差值。可见匹配追踪就是利用式(3)描述的一个重复迭代过程，若迭代m次，则可将f表示为如下形式：

(4)

因此经过m次分解计算后，原始信号可表示为m个匹配子波的线性组合，其误差为第m-1次迭代计算后的差值。虽然MP算法是属于非线性迭代过程，但能量有限的特点可以保证它的收敛性。

由于Gaussian 函数具有良好的时频聚集性，一般选用Gabor原子构建原子库。先将此基函数的时频参数进行离散化，形成过完备的原子库，原子库中Gabor原子可表示为：

(5)

在通过将待分解的信号逐次从原子库中进行比对迭代，直至差值满足一定的条件。该方法的缺点是计算量大，运算速度慢。

1.2双参数匹配追踪算法

匹配追踪的最佳基函数求解实质涉及到多极值优化求解，传统的匹配追踪算法采用的是贪心算法，虽能获得全局最优解但存在计算量庞大的不足。在保证对信号分解精度的基础上，不少人对如何提高匹配追踪运算效率进行了大量研究[14-16]，考虑到Gabor原子受振幅、频率、中心时间和相位四个参数控制，对过完备原子库的扫描实质上是对四个参数的整体寻优过程，若能根据实际情况提前获取某些参数的取值范围，便能降低基函数的扫描范围，提高算法运算速率。

利用Hilbert变换可提前提取其瞬时频率和相位，但Hilbert变换要求原始信号为单频率信号，爆炸地震波信号明显不符合这一条件。由于可将爆炸地震波信号可看成由一定数量的子波组成，这也是进行匹配追踪的前提。再此基础上，可对爆炸地震波信号进行Hilbert变换，获取优势频率范围，再建立动态子波库[17]，再基于此在有限的动态子波库范围内进行匹配搜索，可以有效降低运算量，提高运算速率。

具体算法步骤如下：①离散化Gabor基函数的时频参数，形成原子库Di(i=1，2，…，I)；②将原始信号X(t)赋值给初始差值信号r0；③用Hilbert 变换计算差值信号rm(m=0，1，2，…，M-1)；④计算信号的瞬时包络、瞬时相位和瞬时频率；⑤找到包络最大值及其对应的时间位置，计算相应时间处的瞬时频率和瞬时相位，得到Gabor函数相位角和主频的估计值；⑥将差值rm从限定的原子库中找出与原始信号最匹配的原子dmi，求出匹配细数cmi，并将差值减去匹配原子，得到新差值信号rm+1；⑦重复步骤③～⑥步，直到差值小于一定的阈值，完成了对信号X(t)的分解：

(6)

1.3算法复杂度比较

假定对一长度为N的信号进行匹配追踪分解，为了保证原子库的过完备性，需对四个参数进行过完备扫描，对中心时间u和频率v扫描的计算复杂度均为O(N)，振幅扫描计算复杂度为O(log2(N))，相位参数在0～2π之间扫描，故传统过完备匹配追踪算法复杂度为(N2.log2(N))。而双参数匹配追踪算法已获取频率相位参数信息，其算法复杂度为O(N.log2(N))，运算速率明显提高，且分解信号长度越长，双参数匹配追踪算法运算速率优势越大，更适合处理数据量大的地震波信号。

1.4基于匹配追踪算法的时频分析

时频分析是地震信号数据处理中一种非常重要的信号处理方法，把地震数据变换到频率域是一系列重要地震资料处理算法和解释技术的基础。WVD是由瑞利(Ville)引进信号分析的并对魏格纳分布给出了一个似乎合理的论证，并根据特征函数方法推导得出[18]。

信号X(t)的WVD如下：

(7)

由于式中不含有任何的窗函数，因此避免短时傅里叶变换时间分辨率与频率分辨率相互牵制的矛盾，它的时间-带宽达到了测不准原理给出的下界。但是维格纳-瑞利分布本质不是线性的，即两信号和的 WVD并不等于每一个信号的 WVD之和。令X(t)=X1(t)+X2(t)，则

Wx1(t,ω)+Wx2(t,ω)+2Re[Wx1+x2(t,ω)]

(8)

式中:2Re[Wx1+x2(t,ω)]是X1(t)和X2(t)互WVD，称之为交叉项。

由式(8)可以看到：有时魏格纳分布在时间和频率上把这些值置于两个信号的中间；有时这些值又处在时-频平面和所期望的东西争夺位置。因此产生了交叉项。交叉项极大的干扰时频分布，同时也抑制了二次型时频分布的推广。若能结合匹配追踪算法，将信号分解成基本原子的线性叠加，分别对每个信号做WVD，在将其叠加，能达到很好的时频分析效果。例如，图1是由四种频率成分的调制信号。

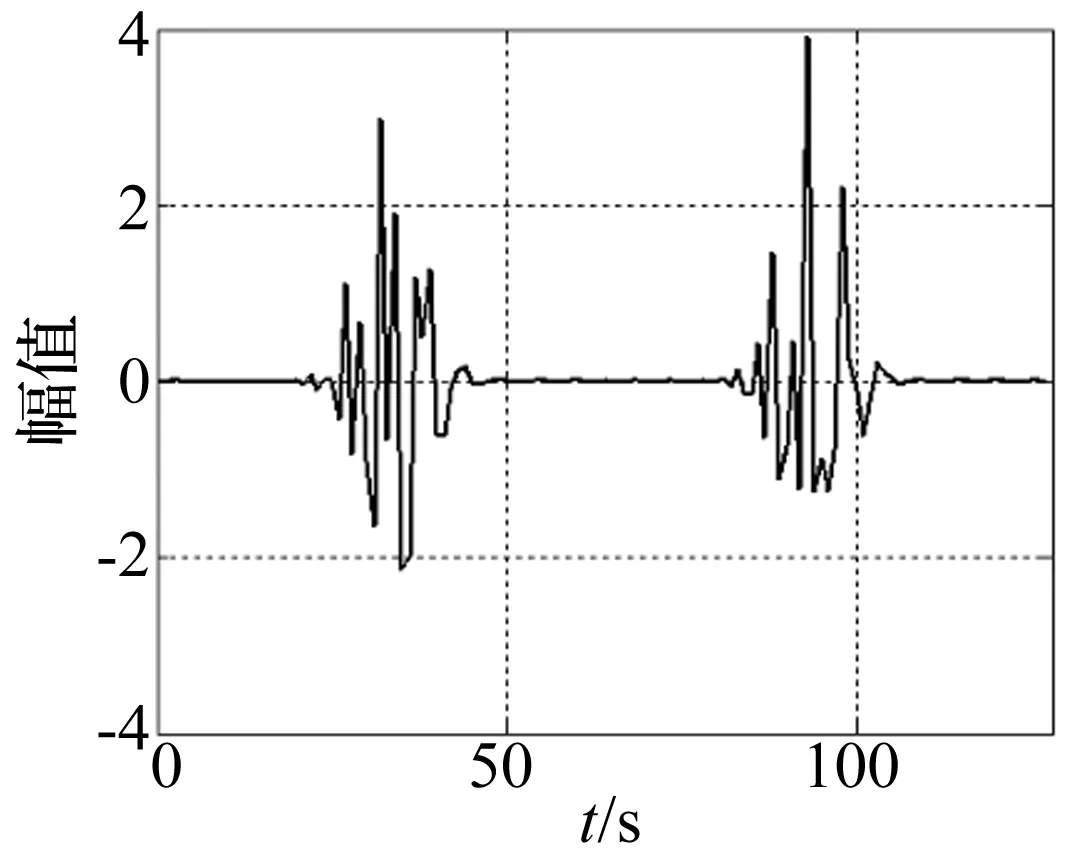
图1　四频率成分信号Fig.1　Signals with four frequencies

分别直接计算WVD和对其进行子波分解后计算WVD，结果如图2所示。

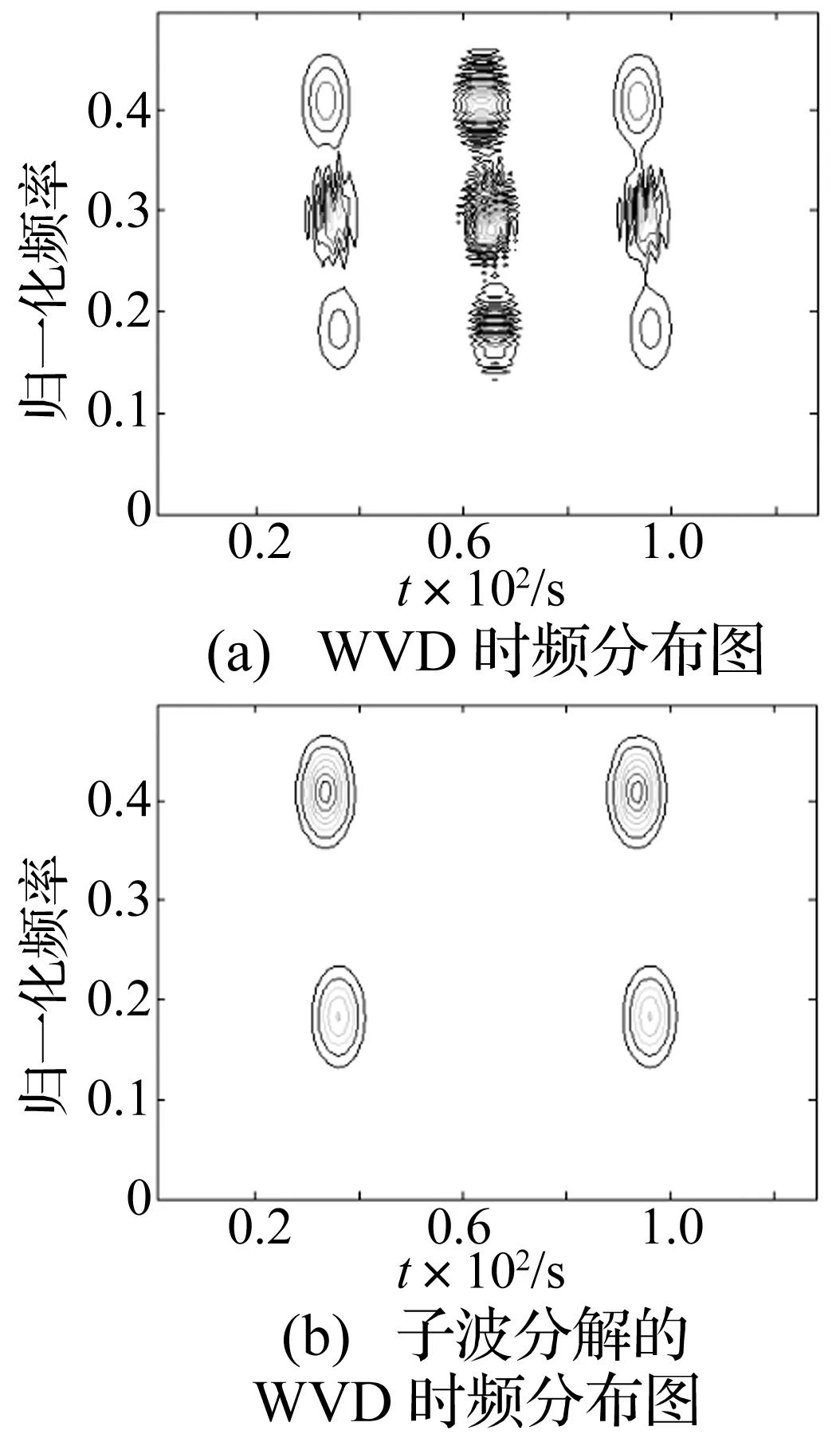
图2　Wigner-Ville 时频图Fig.2　Time-frequency of Wigner-Ville distribution

在图2(a)中，处理后的信号细节部分主要集中在三个时间段和三个频率段上，而原始四频率成分信号主要是由两两频率或相位相近的信号组成，这表明处理后的信号并不能很好的还原原始合成信号的细节部分。这是因为由式(8)可以看到WVD是在时间域和频率域将这些值置于两个信号之间，产生了干扰项。四频率成分信号两两相互形成干扰项，共产生 6 个交叉项(其中中间阴影部分的交叉项为重叠交叉项，为由左上与右下交叉项和左下与右上交叉项的重叠)。

若将WVD对t进行积分，可以得到：

(9)

式(9)表明，若将WVD在某频率处对t积分等于该频率处的能量谱。

2　不同孔深土中爆炸试验

2.1试验方法

本次试验的方法是进行多组不同孔深的爆炸试验，装药选用的是75 gTNT药柱，采用电起爆法。分组进行试验，孔深依次为0 m、0.2 m、0.4 m、0.5 m、0.6 m、0.8 m。炸药竖直放置在孔底部，不回填。试验方案(见图3)。

图3　土中爆炸试验方案Fig.3　Testing program of the explosion in earth

分别在距离炮孔3 m、4 m、5 m处布置传感器。传感器采用中国地震局工程力学研究所研制的891-Ⅱ型磁电式拾振传感器，主要用于感应地震波、机械振动和各种冲击信号。爆破测震仪采用成都中科测控有限公司生产的TC-4850型爆破测震仪，主要用于对地震波、机械振动和各种冲击信号进行记录。仪器为自适应量程，一般为35 cm/s。试验现场布置(见图4)，设置仪器采样时间为10 s，采样率8 kHz。

各组试验具体的爆破参数见表1

图4　现场试验布置Fig.4　Field test arrangment

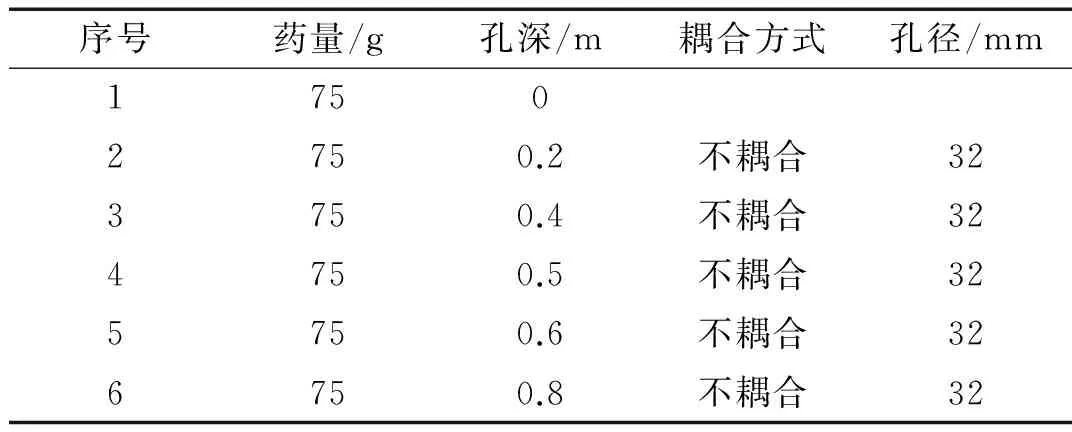
表1　孔深试验爆破参数

2.2试验结果

根据试验所测地震波数据得到各测点不同孔深土中爆炸地震波质点振动速度峰值主频情况见图5。

由图5(a)可知随着孔深增加，地震波质点振动速度增大，表明炸药的能量更多的作用于土壤内部，较少的耗散到空气中，使得地震波的能量增大；当在地面爆炸时，产生的地震波明显较土中爆炸产生的地震波弱。

图5　各测点处振动峰值与主频Fig.5　The vibration peak and main frequency of each measuring point

由图5(b)可知，地面爆炸产生的地震波主频较高，而土中爆炸产生的爆炸地震波主频低，为几十赫兹(Hz)。表明高频分量的地震波在土中衰减较快。

3　不同孔深爆炸地震波特性分析

3.1地震波信号分析

利用双参数匹配追踪算法分解爆炸地震波，以孔深60 cm，5 m处测点为列，分解结果见图6。

图6　爆炸地震波信号分解Fig.6　Decomposition of explosion seismic wave

图6为在使得残差信号比原始信号低一个数量级的标准下进行的分解，因其算法复杂度为O(N.log2N))，较过完备匹配追踪少一个信号长度，使得其运算速率明显提高。选定的残差信号标准保证了分解结果的有效性和准确性，并达到了去噪的效果，更能反应实际地震波特性。对其进行时频分析，得到其WVD和频谱能量图见图7。

图7　爆炸地震波时频分析Fig.7　Time-frequency analysis on explosion seismic wave

由图可知爆炸地震波能量谱有较高的分辨率，地震波能量集中在低频部分，且主频处的能量并不一定为爆炸地震波频谱能量的峰值。

3.2不同孔深地震波特性分析

分别计算爆炸地震波频谱能量，得到最大能量及其对应的频率如图8所示。

图8　各测点频谱峰值能量及应频率Fig.8　The peak energy and frequency of each test points

由图8可知，在一定深度范围内，孔深增加，爆炸地震波峰值能量增加，更多的向低频分量集中，高频分量衰减更严重，但当孔深超过一定深度时，峰值能量和频率变化不大，表明此时孔深的影响较小。因此，浅孔爆破时，孔深对土中爆炸地震波频谱能量有较大影响，在进行爆炸地震波危害防护时应予以考虑。

为了进一步量化分析不同孔深爆炸地震波特性，分别计算不同孔深爆炸地震波峰值能量随传播距离的衰减斜率，计算结果如图9所示。

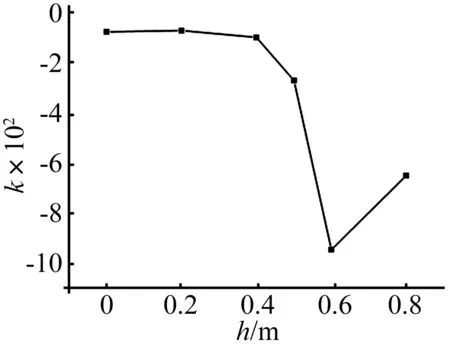
图9　不同孔深处爆炸地震波峰值能量衰减斜率Fig.9　The slope of peak energy attenuation with different hole depth

计算结果表明，在一定深度范围内，孔深增加，爆炸地震波的能量衰减更严重，但当深度超过一定范围时，爆炸地震波峰值能量衰减不再增加。

4　结　论

(1) 双参数匹配追踪算法能够极大的提高分解信号的运算速率，符合处理大量地震信号数据的需求；

(2) 利用匹配追踪分解地震信号后进行WVD计算，能够充分利用其没有窗函数的高分辨率的优势并能很好消除其交叉干扰项的影响；

(3) 在一定范围内，孔深增加，爆炸地震波峰值能量增加，高频衰减更严重，当孔深超过一定深度时，爆炸地震波峰值能量衰减不再增加；

(4) 浅孔土中爆破作业时，在进行爆炸地震波危害防护时应予以考虑合理的孔深参数。

[1] 张义平，吴桂义. 爆破地震波特性研究[J]. 矿业研究与开发，2007，27(6)：68-72.

ZHANG Yiping, WU Guiyi. Study on characteristics of blasting-caused seismic wave[J]. Mining R & D,2007,27(6):68-72.

[2] 龙源，冯长根，徐全军，等. 爆破地震波在岩石介质中传播特性与数值计算研究[J]. 工程爆破，2000，6(3)：1-7.

LONG Yuan, FENG Changgen, XU Quanjun, et al. Study on profagation characteristics of blasting seismic waves in a rock medium and nuerical calculation[J]. Engineering Blasting, 2000, 6(3): 1-7.

[3] 施鹏，邓国强，杨秀敏，等. 土中爆炸地冲击能量分布研究[J]. 爆炸与冲击，2006，26(3)：240-244.

SHI Peng, DENG Guoqiang, YANG Xiumin, et al. Study on ground shock energy distribution of explosion in soil[J]. Explosion and Shock Waves, 2006, 26(3): 240-244.

[4] 赵跃堂，郑大亮，王明洋，等. 饱和土介质中爆炸波传播的时间特征试验研究[J]. 防灾减灾工程学报，2004，24(2)：162-167.

ZHAO Yuetang, ZHENG Daliang, WANG Mingyang, et al. Experimental investigation on time characteristics of explosive wave propagation[J]. Journal of Disaster Prevention and Mitigation Engineering, 2004, 24(2): 162-167.

[5] 施鹏，辛凯，杨秀敏，等. 土中装药不同埋深爆炸试验研究[J]. 工程力学，2006，23(12)：171-174.

SHI Peng, XIN Kai, YANG Xiumin, et al. Experimental study of explosion with different burial depths soil[J]. Engineering Mechanics, 2006, 23(12): 171-174.

[6] 李兴华，龙源，纪冲，等. 基于小波包变换的高程差对爆破震动信号影响分析[J]. 振动与冲击，2013，32(4)：44-47.

LI Xinghua, LONG Yuan, JI Chong, et al. Influence of height difference based on wavelet packets transformation on blasting vibration signals[J]. Journal of Vibration and Shock, 2013, 32(4): 44-47.

[7] XING Xiaojun, HE Xilei, PU Yong, et al. High-precision frequency attenuation analysis and its application[J]. Applied Geophysics, 2011, 8(4): 337-343.

[8] MALLAT S, ZHANG Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Trans Signal Processing，1993,41(12): 3397-3415.

[9] WANG Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics,2007,72(1):13-20.

[10] 刘继承，富爽. 基于MP算法的快速地震信号谱分析[J]. 计算机技术与发展，2010，20(7)：231-234.

LIU Jicheng, FU Shuang. Fast spectral analysis of seismic signal based on matching pursuits algorithm[J]. Computer Technology and Development, 2010, 20(7): 231-234.

[11] 赵中华，王文延. 基于时频分析的去除魏格纳交叉干扰项的方法[J]. 北京交通大学学报，2010，34(6)：81-85.

ZHAO Zhonghua, WANG Wenyan. Simulation of method to eliminate cross-term in wigner distribution based on matching pursuits in time-frequency domain[J]. Journal of Beijing Jiaotong University, 2010, 34(6): 81-85.

[12] 黄玱，金河. 地震资料复数道分析的解释基础和应用[J]. 石油物探，1984，22(3)：1-19.

HUANG Qiang, JIN He. The oretical basis for interpretation of the seismic data by complex trace analysis and its application[J]. Geophysical Prospecting for Petroleum, 1984, 22(3): 1-19.

[13] 武国宁，曹思远，孙娜. 基于复数道地震记录的匹配追踪算法及其在储层预测中的应用[J]. 地球物理学报，2012，55(6)：2027-2034.

WU Guoning, CAO Siyuan, SUN Na. Matching pursuit method based on complex seismic traces and its application of hydrocarbon exploration[J]. Chinese Journal of Geophysics, 2012, 55(6): 2027-2034.

[14] 邵君. 基于MP的信号稀疏分解算法研究[D]. 北京：中国科学院研究生学院(软件研究所)，2002.

[15] 熊纯，何卫锋. 基于匹配追踪算法的自适应时频分解改进及应用[J]. 长沙航空职业技术学院学报，2007，7(4)：44-48.

XIONG Chun, HE Weifeng. Application of adaptive time-frequency decomposition with modified matching pursuit [J]. Changsha Aeronautical Vocational and Technical College Journal, 2007, 7(4): 44-48.

[16] 孟庆丰. 信号特征表示方法与应用[D]. 西安：西安电子科技大学，2006.

[17] 张繁昌，李传辉，印兴耀. 基于动态匹配子波库的地震数据快速匹配追踪[J]. 石油地球物理勘探，2010，45(5)：667-673.

ZHANG Fanchang, LI Chuanhui, YIN Xingyao. The fast matching pursuit of seismic data based on dynamic matching library [J]. Oil Geophysical Prospecting, 2010, 45(5): 667-673.

[18] 王培茂. 地震信号时频特征表示方法[D]. 长春：吉林大学， 2008.

Characteristics analysis of explosion seismic waves with different hole depth based on the method of double parameters matching pursuit

ZHOU Hui, LONG Yuan, ZHONG Mingshou, XIE Xingbo, GUO Tao

(College of Field Engineering, PLA University of Science & Technology, Nanjing 210007, China)

Taking advantage of the non-stationary random nature of explosion seismic signals, and using the Hilbert transformation to covert the signal into a plurality signal, the two parameters, namely the instantaneous frequency and phase parameter of the signal were acquired. The method of double parameter matching pursuit was introduced to decompose explosion seismic wave signals. The scan efficiency of the matching pursuit (MP) algorithm, the complexity of the algorithm, and the operation rate of the algorithm were effectively improved compared with the ordinary complete matching pursuit algorithm. With resorting to the Wigner Ville distribution, in which the influence of its cross interference terms was effectively eliminated, the time-frequency characteristics of the explosion seismic waves with different hole depth were analysed. The results show that: in a certain depth range, with the increase of hole depth, the energy of the seismic wave is increased, while the attenuation of the explosion seismic wave energy of high frequency also becomes more intense. When the hole depth is over a certain value, the attenuation of the explosion seismic wave energy of high frequency remains at a stable level.

double parameter; matching pursuit; WVD; hole depth; explosion seismic wave

国家自然科学基金项目(51304218;51178460)

2015-10-09修改稿收到日期：2016-03-16

周辉 男，博士生，1990年生

龙源 男，博士，教授，1958年生

E-mail:long_yuan@sohu.com

TB236

A DOI:10.13465/j.cnki.jvs.2016.14.013