高动态DS/FH信号的载波捕获技术研究

董汉清，王玉文，孟凡计

（电子科技大学航空航天学院，四川 成都　611731）

高动态DS/FH信号的载波捕获技术研究

董汉清，王玉文，孟凡计

（电子科技大学航空航天学院，四川 成都611731）

针对高动态跳频信号的载波同步技术问题，提出一种混合域联合估计算法，包括基于时域的扩展卡尔曼滤波和基于频域的FFT算法。理论研究和仿真结果表明：直扩载波捕获可以在一个跳频时隙内完成，继而引导跳频端同步跟跳，满足系统要求。

直扩/跳频；高动态；扩展卡尔曼；快速傅里叶变换

0　引　言

DS/FH体制是在直接扩频的基础上增加了载波跳变，可以提高系统的抗干扰性能，已经成功应用在通信领域[1]，但在航天测控领域还处于理论研究阶段。主要原因是测控距离远、卫星运动速度快，导致产生的多普勒频移和频移变化率非常大，在接收端进行的载波捕获非常困难[2]。本论文针对这一课题，提出了一种混合多普勒频移补偿算法，可以在一个跳频时间间隔内快速而精确地捕获多普勒频移值。

1　算法分析

航天测控系统中，由于高速运动的卫星会对测控信号产生高动态的多普勒频移值。在跳扩频体制的测控系统中，接收到的信号会随着跳频码的快速跳变而改变其载波频率。在10000跳/s的情况下，每个驻频点的时间间隔仅为0.1ms，如果在这段时间内不能快速捕获并补偿多普勒频移值，那么测控伪码就会移位[3]。不同于直接序列扩频体制的是，在跳频体制下，由于每个跳频段的载波和多普勒频移值的不同，会导致各段伪码偏移值的不同，最终无法解调出正确的伪码，无法达到测控的目的。

本文在考虑上述情况下，提出了一种结合扩展卡尔曼滤波和FFT的多普勒频移捕获算法：对接收到的信号进行下变频后，得到中频信号。首先对下变频信号进行扩展卡尔曼滤波，由于扩展卡尔曼滤波具有在较少数据的情况下进行快速估计的性能，所以能够快速获得多普勒频移的大致范围，同时通过反馈回路对估计出的多普勒进行频移补偿[4]。之后对残余多普勒频偏进行非线性变换和数据抽样变换，用FFT对粗估计的信号进行精确多普勒频移估计和补偿，其算法流程如图1所示。

图1　算法流程图

1.1基于扩展卡尔曼滤波估计算法

扩展卡尔曼滤波是将卡尔曼滤波思想扩展到非线性模型[5]。对于多普勒频移估计，接收到的信号经过降频处理后的实部和虚部表示为

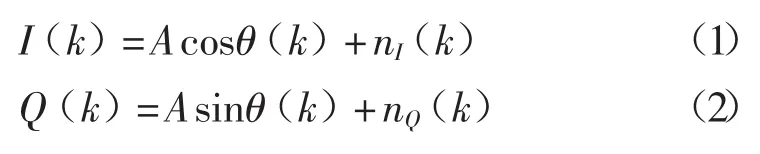
相位θ（t）定义为多普勒频率fd（t）的积分形式：

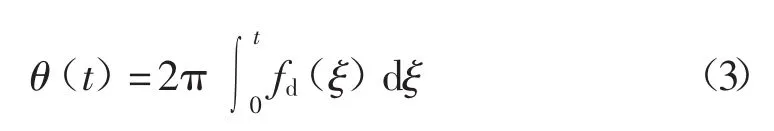
在t0点对多普勒频率fd（t）进行泰勒级数展开：

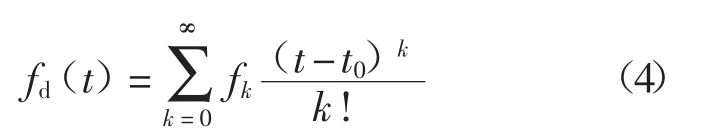
在t=t0时将t0=0时的多普勒二阶表达式带入相位表达式得到：

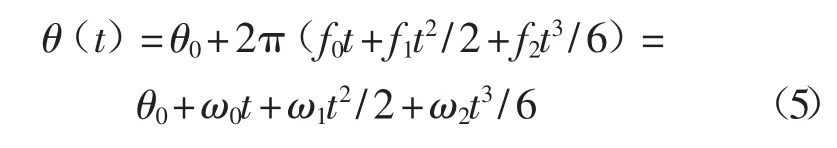
对于扩展卡尔曼滤波，相位可视为频率轨迹的积分函数，并对其进行估计。

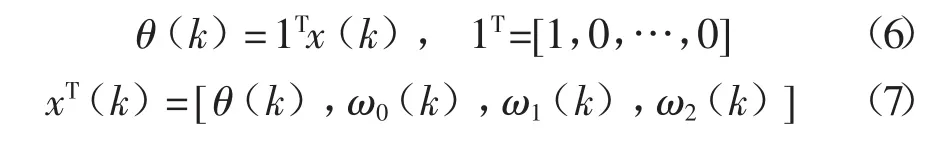
它们的关系如下：

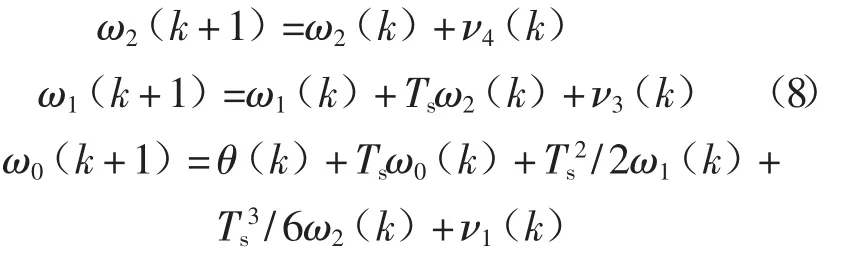
状态方程转移矩阵Φ：

其中Q为噪声干扰矢量的协方差矩阵：

综上，通过扩展卡尔曼滤波算法对状态向量x（k）的估计过程如下：

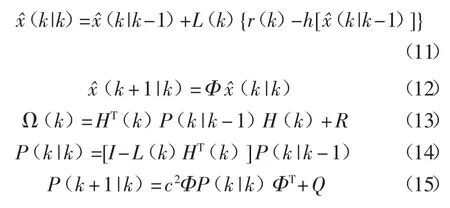
式中：R=δn2I，δn2为噪声均方误差，δn2=N0/2Ts；

c——标量因子；

HT（k）——h[x（k）]的线性化因子。

1.2基于FFT的改进算法

在T时间内接收到的信号经采样后表示为

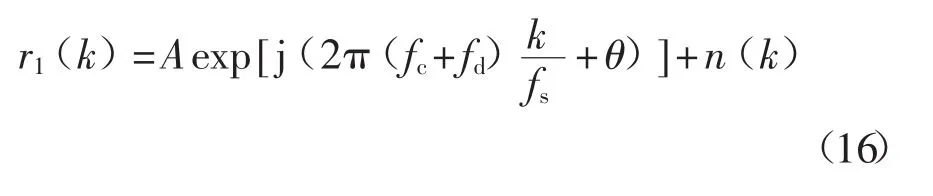
式中：A——信号的幅度；

fc——载波信号的频率；

fd——多普勒频移；

fs——信号的采样频率；

n（k）——高斯白噪声。

信号经过下变频后表示为

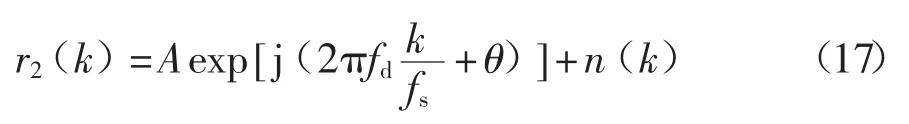
FFT的计算精度与其采样率成正比，如果想得到高精度的多普勒频移值[6]，就要求很大的采样数据，进而增加的FFT运算复杂度和时间，在DS/FH测控系统中是不能接受的。

本文对FFT算法进行改进，将粗估计后的信号进行抽取滤波，这样就可以降低采样率，同时对多普勒频移值进行倍频处理。

假设抽取滤波器的抽取因子为R，则抽取后信号采样频率为抽取前的1/R：

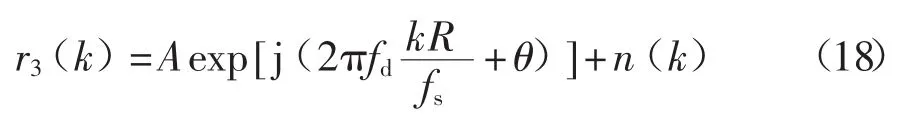
在高动态环境下，滤波器往往要通过增加带宽来满足大多普勒频移的要求，而这样会使信号的信噪比大幅降低。针对这一问题，可对信号进行自相关处理：

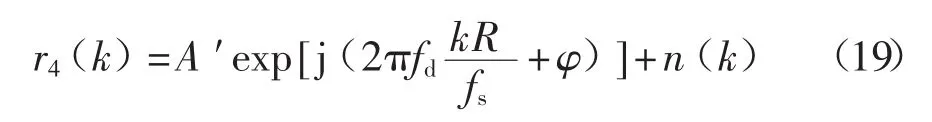
根据自相关原理，信号的幅度和相位值发生了改变，不变的是信号的频率，即多普勒频移值没有变化。而新产生的噪声n（k）要比原来的噪声n（k）小，从而提高了信噪比。

对自相

关运算信号r4（k）进行FFT变换，便可在频域上精确地估计出信号多普勒频移，从而得到数据信号的多普勒频移。

抽取滤波器的抽取因子为R的FFT变换的分辨率为

当FFT变换的点数N一定时，频率分辨率精度与抽取因子R的大小有关。在合理范围内，抽取因子R越大，FFT频移估计算法精度越高[7]。

经过扩展卡尔曼滤波的多普勒频移粗估计和频移补偿之后，多普勒频移远远小于采样率，根据奈奎斯特准则，采样率必须大于两倍的频移值，这样就可以将多普勒频移进行倍频处理，进一步提高FFT的计算精度[8-10]。

倍频系数为K的FFT变换的分辨率表示为

综上所述，经过扩展卡尔曼粗估计和多普勒频移补偿后，信号中的残余多普勒频移再经过抽取和倍频，就可以在FFT精估计时，大大提高多普勒频移的估计精度，其最终的估计值为

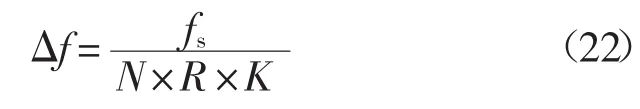
2　计算机仿真

2.1仿真模型

本系统采用的跳频系统跳速为10 000跳/s，跳频驻留时间为0.1ms，跳频频率量化间隔选为10kHz，直扩PN码速率为20Mchips/s，直扩码码长255位，跳频点数为128点，载波为25GHz。接收端匹配滤波器长度为4096位，多普勒频率设置为900kHz。

2.2多普勒频移对接收信号的影响

当伪码完全对齐的情况下，载波多普勒频移引起的频率偏移差对相关峰值检测的影响如图2所示。可以看出，当频率偏差fd等于0.5倍的信息速率Rb时，信号相关峰值下降约3dB。

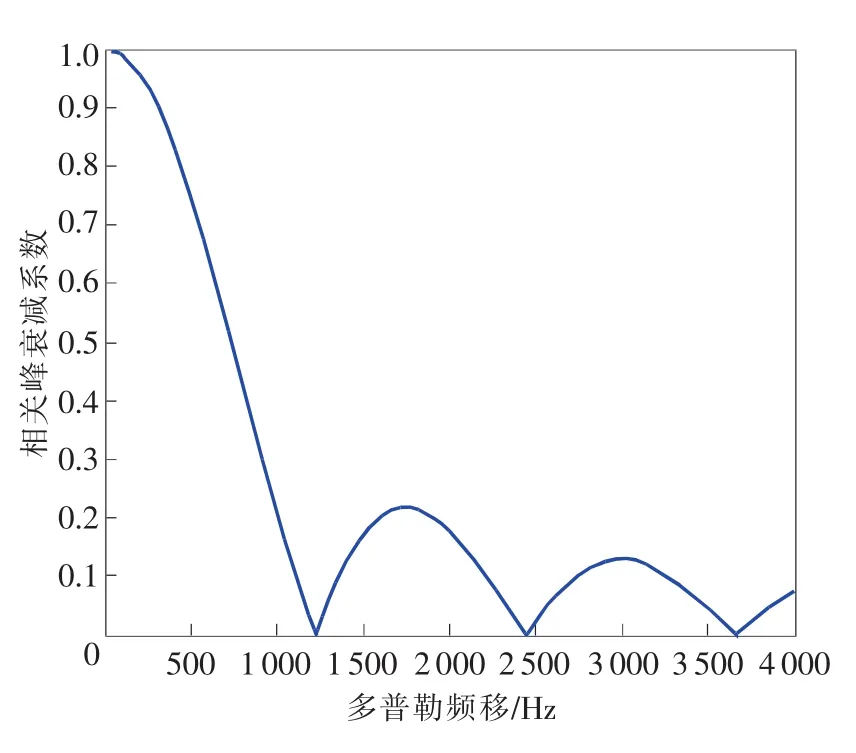
图2　多普勒频移对相关峰衰减系数的影响图

2.3多普勒频移的估计

多普勒频移估计的均方误差（MSE）表达式为

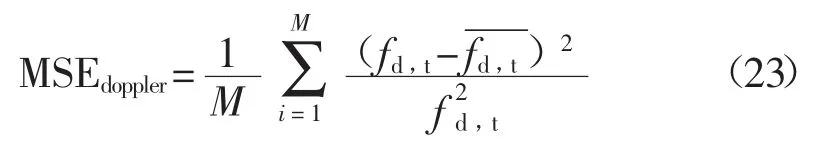
当信噪比SNR=10dB，多普勒频移为900kHz条件下，扩展卡尔曼滤波算法在不同数据点数下的估计性能曲线如图3所示。

图3　扩展卡尔曼滤波在不同点数的估计性能

从图中可以看出，扩展卡尔曼滤波在数据点数较少的情况下，可以快速估算出多普勒频移的大致范围，当数据点数增多时，扩展卡尔曼滤波算法的估计精度区域平稳，根据这一特点，系统采用4000点数据仿真，多普勒频移值的误差为540Hz，为下一步的精确估计缩小范围和计算量。

表1　仿真条件

仿真在表1所示的数据条件下进行，其中倍频因子和抽取因子都受限于采样频率，不宜过高，得到精确估计的多普勒频移值为

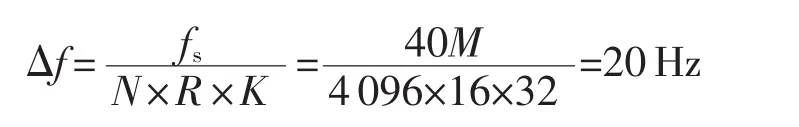
图4为联合估计算法和FFT算法对多普勒频移值的估计结果，可以看出，经过两次估计的联合估计算法大大提高了多普勒频移的估计精度。

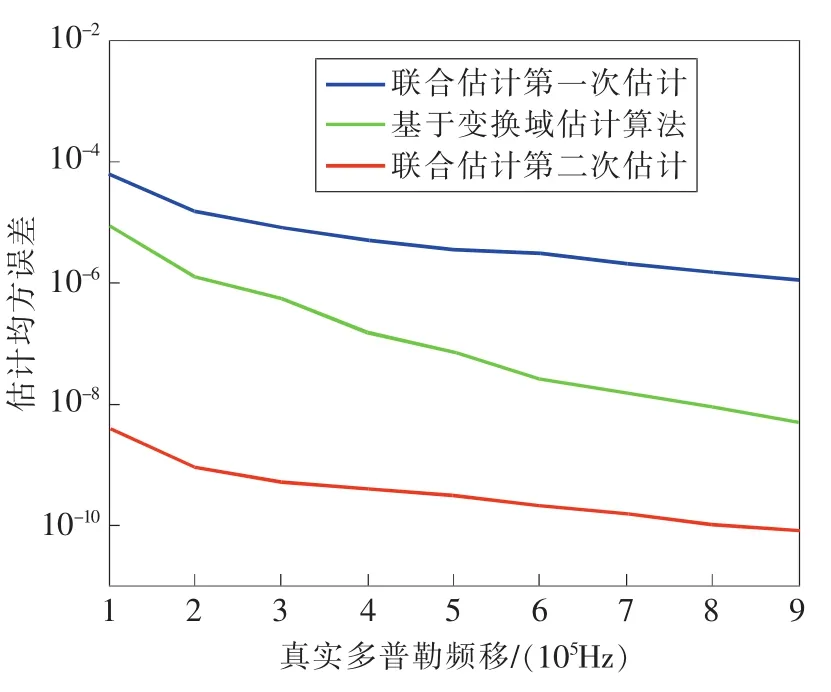
图4　各算法的评估性能比较

图5是联合估计算法所需要的时间0.051 ms，满足一个跳频驻点时间0.1 ms。捕获结束后，通过反馈回路对载波进行多普勒频移补偿结束后，如图5所示，多普勒频移被消除掉。

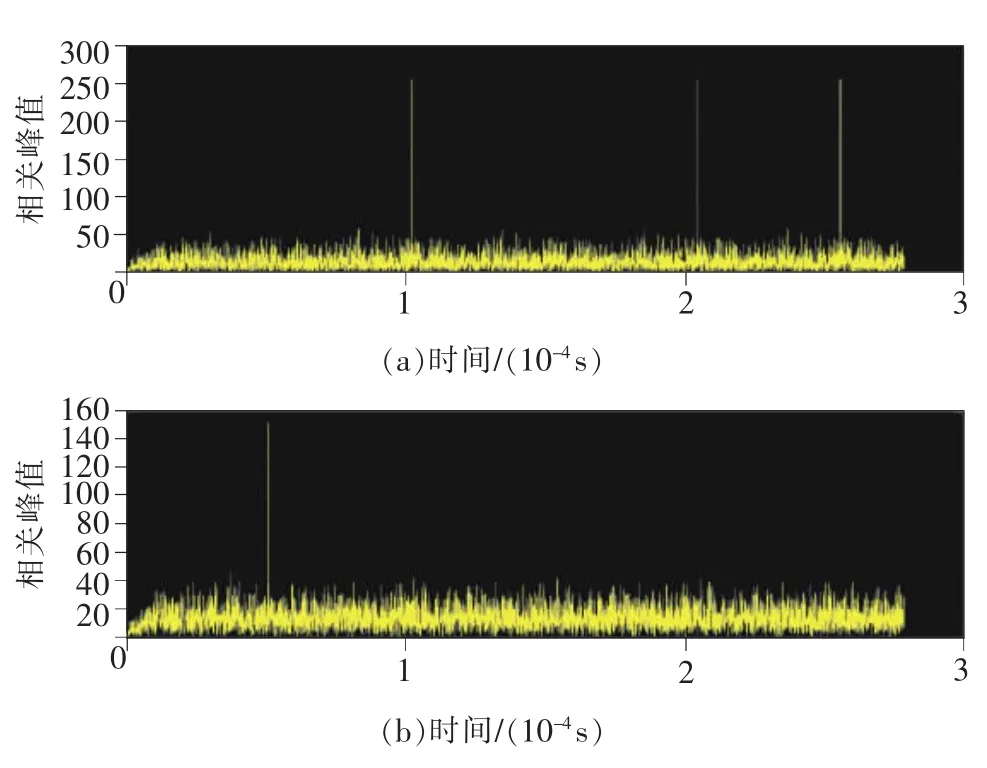
图5　联合估计算法的时间测试

3　结束语

DS/FH系统有着优越的抗干扰特性，备受国内外学者的青睐，由于跳频系统的特殊性，使得其多普勒频移和多普勒频移变化率都非常大，而且允许的捕获时间非常短暂，传统的捕获方法已经不能满足要求。

本文借鉴了直接扩频测控系统的捕获方法，通过改进，设计出一种满足跳扩频测控系统的多普勒频移补偿方法，将扩展卡尔曼滤波算法和FFT算法相结合，通过Matlab仿真验证，实现了载波多普勒频移的实时高精度捕获。

[1]田日才.扩频通信[M].北京：清华大学出版社，2007：143-148.

[2]杨昂.高动态环境下多普勒频移估计技术研究[D].西安：西安电子科技大学，2011：45-52.

[3]陈静.DS/FH混合扩频测控信号同步及抗干扰研究[D].成都：电子科技大学，2009：38-41.

[4]杨文革，孟生云，王金宝.DS/FH扩频测控信号的一种同步方案分析[J].电视技术，2009，49（6）：5-9.

[5]周靖宇，田书林.利用Simulink及AWG产生扩跳频通信信号的方法[J].中国测试，2011，37（1）：74-76.

[6]孙峰，金炜东，王博.基于扩展卡尔曼滤波的高动态多普勒频移估计[J].现代电子技术，2009，32（8）：69-71.

[7]童卓，王东进，刘发林.低轨卫星的多普勒频移实时估计[J].中国科学技术大学学报，2004，34（2）：190-195.

[8]黄振，陆建华，杨士中.卫星通信中多普勒频移的快速捕获[J].电子学报，2003，31（7）：1052-1056.

[9]刘美生.全球定位系统及其应用综述——导航定位技术发展的沿革[J].中国测试，2006，32（5）：1-7.

[10]刘剑锋，王虹淞，李云.卫星移动通信多普勒频移补偿研究[J].重庆邮电大学学报（自然科学版），2014，26（3）：352-357.

（编辑：徐柳）

Study of carrier capture for high dynamic DS/FH signals

DONG Hanqing，WANG Yuwen，MENG Fanji
（Institute of Aeronautics and Astronautics，University of Electronic Science and Technology of China，Chengdu 611731，China）

The main reason is its complex Doppler shift under high dynamic characteristics.For the carrier synchronization problem of high dynamic frequency hopping signals，a mixed-domain joint estimation algorithm has been proposed.The algorithm consists of the extended Kalman filter based on the time domain and FFT algorithm based on frequency domain.The theoretical studies and simulation results show that DS carrier capture can be done in the time slot of a frequency hopping，and then guide the hopping side to synchronize with the jump，which meet the system requirements.

DS/FH；high dynamic；EKF；FFT

A

1674-5124（2016）03-0099-04

10.11857/j.issn.1674-5124.2016.03.023

2015-01-21；

2015-03-09

董汉清（1986-），男，山东荷泽市人，硕士研究生，专业方向为航空航天测控、通信技术。