不同偏最小二乘法在化学需氧量近红外光谱特征波段选择中的应用
2016-10-16朱乾华杨季冬
杨 琼, 朱乾华, 任 鹏, 龙 帅, 杨季冬*,2
(1.长江师范学院化学化工学院,重庆 408100;2.重庆三峡学院化学及环境工程学院,重庆 404000;3.西南科技大学生命科学与工程学院,四川绵阳 621010)
化学需氧量(COD)为水体受污染程度的重要计量指标之一,因此,研究 COD 的测定方法具有重要意义。COD传统的检测方法有重铬酸盐法[1]、高锰酸钾法[2]以及其它的方法[3,4],但这些化学分析法操作繁琐,需用重金属药品,可能造成二次污染。因此,建立一种快速无损且高效的COD的分析方法很有必要,近红外光谱分析技术就能达到这一要求。
近红外(NIR)光谱技术具有快速、准确、简单和成本较低等优点,因此得到各行业的青睐[5],且在COD检测领域迅速发展[6,7]。近红外光谱分析结果的准确性,取决于模型的合理使用和定标模型的质量好坏,所以必须选择合适的模型建立方法。偏最小二乘法(PLS)是光谱数据处理常用的方法之一,且在使用中对其进行了改进[8],并发展了间隔偏最小二乘法(iPLS)、前向、后向间隔偏最小二乘法(FiPLS,BiPLS)等建模方法。PLS法一般利用全波谱建立模型,为了尽可能选择灵敏度较高的波段,以简化模型、提高模型精度。本文在利用近红外光谱法结合PLS研究COD的基础上,提出一种基于iPLS、FiBLS和BiPLS的COD近红外光谱特征波段选择方法。将全谱波段等分为30、20、15、12个子区间,以PLS算法对全谱波段和每个子区间单独进行回归建模,然后以FiPLS 和BiPLS算法对各个区间进行重新组合并得出优化结果模型,用预测集标准偏差(RMSEP)和交叉验证均方差(RMSECV)作为模型的评价参数。结果显示:全波段所建立的PLS的选择效果最差,iPLS、FiPLS、 BiPLS选择效果均有所改进,且BiPLS算法提升的效果最好。
1 实验部分
1.1 仪器与药品
日立U-4100 紫外-可见/近红外分光光度计;OPUS5.5光谱软件;EL104 分析天平(Mettler-toledo,上海)。
重铬酸钾、硫酸亚铁、邻菲咯啉、硫酸亚铁铵、硫酸银、浓硫酸均为分析纯。实验所用水为超纯水。
1.2 样品的采集和处理
按照环境监测提供的方法在生活污水沉淀池采集120个水样,其中80个样本作校正集,40个样本作预测集,经20 min沉淀后,分为2组,一组测定其COD化学值,一组采集其近红外光谱。COD 化学值测定参照国家标准方法[1]。测得COD标准值的范围为28.40~528.0 mg·L-1。
1.3 光谱采集
使用1 cm 石英池,在波长800~1 800 nm 的近红外区域,以空气为参比,扫描废水样品,波长间隔2 nm,设置狭缝为2 nm,扫描速度为1 500 nm/s,每个样品扫描3次,取平均值为废水的NIR透射光谱图,如图1所示。
1.4 不同PLS选择最佳波段
1.4.1PLS全谱模型PLS法最先产生于化学计量领域[9],用于克服解释变量超出化学样本个数而导致多重相关性问题。本文采用OPUS5.5计量学软件建立PLS模型,采用留一法交互验证(Leave-one-out Cross Validation,LOO-CV)计算RMSECV。
1.4.2iPLS模型iPLS法原理是将预处理后的全光谱模型波段等分成若干子区间,然后逐个将子区间建立待测的PLS回归模型。将得出各组结果中的RMSECV值进行对比,最小的即为最优的建立模型区间。
1.4.3BiPLS模型BiPLS法是在iPLS 的基础上建立的一种算法,BiPLS法是一种对子区间只减不加的方法。方法是将含有n个单独区间整个iPLS模型中逐一去除一个子区间,将剩余的n-1个子区间联合建立PLS 模型,并记录相应的RMSECV值。然后固定剔除局部模型精度低的子区间进入下一轮运算,即去除该子区间之后,所建立的模型得到的RMSECV值最小,以这种方法逐一剔除最差区间,直到只剩一个子区间。将RMSECV值最小的联合模型确定为最优组合。
1.4.4FiPLS模型FiPLS法是一种对子区间只加不减的方法。它的操作方法是将iPLS单独区间模型中RMSECV值最低的子区间作为第一入选区间(若RMSECV值一致,优选相关值大的子区间),然后依次把剩下的n-1个子区间逐一与第一入选区间组合成n-1组联合区间,进行PLS回归建模,以这种循环的方式优选,各最优组逐个联合直到全部区间被同时建模。将RMSECV值最小的联合模型确定为最优组合模型。
2 结果与讨论
2.1 建模样本的划分
预测集样本与校正集样本的划分对数学模型的建立有着重要的作用,校正集样本范围需覆盖预测集样本,如果预测集样本不在校正集样本范围之内,就必须扩充校正集样本。因此,本实验选用80个样品作为校正集样本,40个样品作为预测集样本。样品中校正集化学值范围为19.64~528.0 mg·L-1,平均值为120.4 mg·L-1;预测集化学值范围为41.6~227.2 mg·L-1,平均值为98.38 mg·L-1。
2.2 光谱预处理
从图1可以看出,废水样品的近红外透射光谱图重叠很严重,所以对光谱进行预处理是非常有必要的。本实验对比了原始光谱、多元散射校正、平滑处理、消除常量偏移、矢量归一化、一阶导数以及二阶导数处理等光谱处理方法,结果显示,效果最好的模型是由矢量归一化法对光谱数据进行处理而得到。因此,本实验所有模型的建立均选用矢量归一法对光谱数据进行预处理。
2.3 不同PLS模型的建立
2.3.1PLS模型的建立图1为废水样品波长800~1 800 nm近红外光谱全谱,由图可见该光谱的特征吸收范围应该在800~1 400 nm处,而在其他的波长点处吸收微弱或者没有特征吸收,应该选择该波长范围进行建模。本文光谱预处理使用OPUS软件,选用矢量归一化法在全波进行处理,将最优波段自动选择为800~1 400 nm。一般通过以下几个主要参数评价一个模型的好坏:RMSECV作为局部模型精度衡量标准,相关系数(R2)表示变量间的相关紧密程度;RMSEP反映实测值与预测值的差异,一个模型具有较高的R2,较低且值接近的RMSECV和RMSEP,就是较好的模型。根据选择最优模型的参数,选出了最优模型,其最优模型的RMSECV为18.8 mg·L-1,相关系数(R2)为0.8219。
2.3.2iPLS模型的建立对原始光谱采用矢量归一化法预处理后,确定全波段800~1 400 nm,将全谱每隔20 nm、30 nm、40 nm、50 nm分为30、20、15、12个子区间,将每个子区间利用PLS分别建立回归模型,并选择了各个区间的最优模型,其最优模型的统计结果分别如下表1所示。由表1可以看出,利用iPLS所建立的最佳模型比用全波段所建立的模型各个参数都有所提高。而把全波谱间隔20 nm划分为30个区间所得的最优模型为最佳,所以,选用把全波谱划分为30个子区间来建立后面的FiPLS和BiPLS模型。

表1 iPLS模型的优化结果
2.3.3FiPLS和BiPLS模型的建立因为iPLS只能在一个子区间内建模,没有考虑到多个区间的组合,虽然减少了运算量,但是它也会丢失一些其他区间的有用信息。因此我们在iPLS的基础上,又使用BiPLS和FiPLS建立模型。因为把全波谱间隔20 nm划分为30个区间所得的模型为最优模型,因此,选用把全波谱划分为30个子区间来建立FiPLS和BiPLS模型。两个模型的结果参数如表2所示。
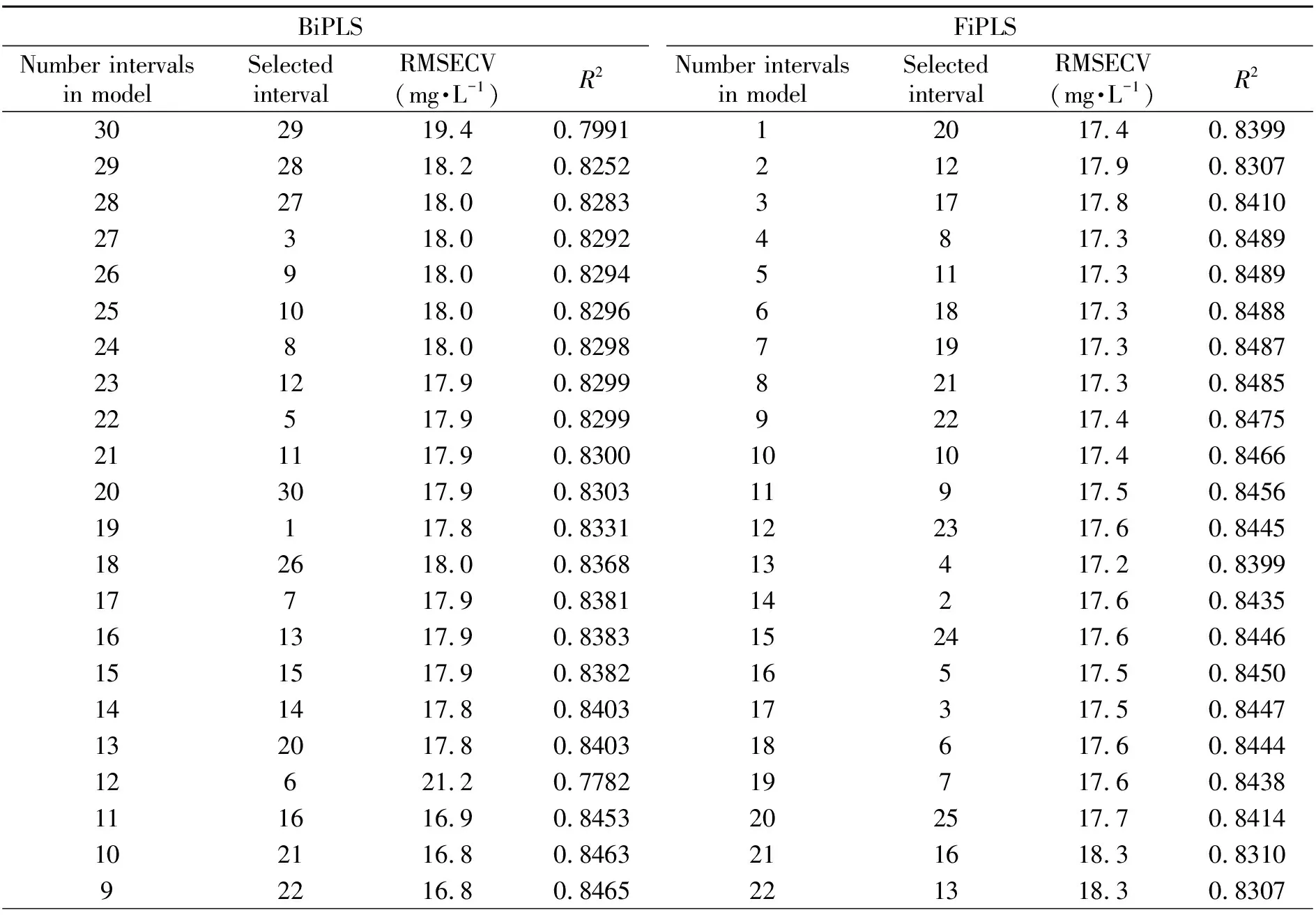
表2 BiPLS和FiPLS的模型参数
(续表2)
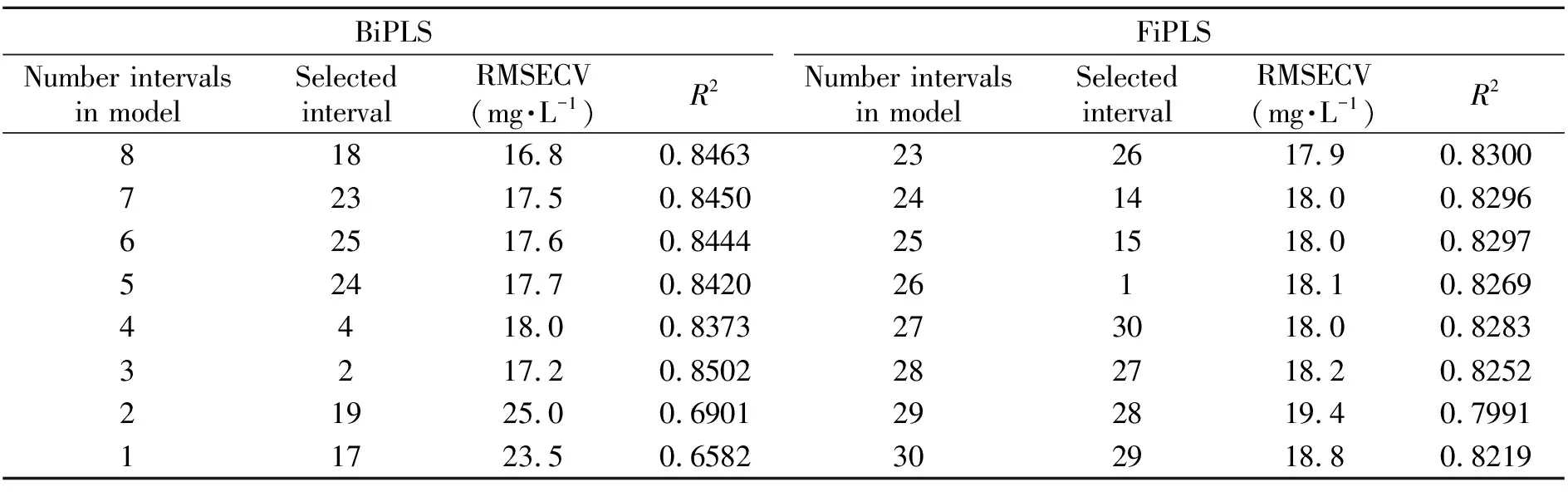
BiPLSFiPLSNumber intervals in modelSelected intervalRMSECV(mg·L-1)R2Number intervals in modelSelected intervalRMSECV(mg·L-1)R281816.80.8463232617.90.830072317.50.8450241418.00.829662517.60.8444251518.00.829752417.70.842026118.10.82694418.00.8373273018.00.82833217.20.8502282718.20.825221925.00.6901292819.40.799111723.50.6582302918.80.8219
从表2可以看出,在BiPLS模型中,当入选区间数达到8、9、10个,此时的模型RMSECV值最小,为16.8 mg·L-1,当入选区间数达到9时,相关系数最大为84.65,故选用入选区间为9时为最佳模型。为剩下参与建模区间序号有22、18、23、25、24、4、2、19、17。在FiPLS模型中,当入选区间数达到13个,此时的RMSECV值最小,为17.2 mg·L-1,入选参与建模的区间序号有20、12、17、8、11、18、19、21、22、10、9、23、4。研究发现BiPLS和FiPLS均比全谱建模的PLS法以及iPLS所得的结果更为精确,且通过BiPLS和FiPLS的对比发现,BiPLS最优组合所得的RMSECV值比FiPLS最优组合的更小,更为精确。所以我们选用参与建模区间序号为22、18、23、25、24、4、2、19、17组合所建立BiPLS模型来测定废水中COD值,其最佳模型的RMSECV为16.8 mg·L-1,R2为0.8465。BiPLS法所建立的模型吸取了PLS全波长建模和iPLS建模的优点,既考虑到多个区间的组合,也减少了运算量。
2.4 最优模型的验证
通常外部验证采用性质与参与建模的校正集样本具有相似的未参与建模样本,为了评价模型的预测准确性,普遍通过对比化学测量值和模型外部预测集样品的预测值差别进行验证。本实验用校正集样本经BiPLS算法优选后的波长范围建立数学分析模型,对预测集样本的COD值进行了预测,其RMSEP为15.9 mg·L-1,R2为0.8265。结果显示近红外光谱预测值和标准方法所测值具有较高的相关性,预测效果达到预期目标。
2.5 最优模型与其它模型的对比
前人利用近红外光谱法对COD研究颇多,我们把本文方法与其他部分文献做了对比,结果如表3所示。从表中可以看出,所列出来的文献所用建模方法均为PLS,波段范围比较广,而我们为了去除全波段中的无用部分来减小运算量,通过研究发现利用BiPLS最优组合所得的RMSECV值与RMSEP值更小,更为精确。其RMSECV和RMSEP分别为16.8 mg·L-1和15.9 mg·L-1。

表3 模型参数对比
3 结论
本文利用近红外光谱法结合PLS、iPLS、BiPLS和FiPLS对废水样品中的COD进行分析,并对近红外光谱特征波段进行了选择。结果表明:iPLS算法较全谱建模更为精确,且有效减少了模型的变量个数,但是改进的BiPLS和FiPLS算法更能体现这一优势,不仅在选择中剔除了噪音多的区间,还能将多个较佳的区间进行组合,但是FiPLS是只加不减的算法,在与BiPLS这种只减不加的算法相比较,更容易被干扰而导致精确度降低,使BiPLS最终结果比FiPLS更佳。所以,BiPLS更适合作为COD近红外光谱特征波段选择的算法。用最优模型对预测集样本的COD的含量进行了预测,获得较好结果。
