光栅最小偏向角法测量汞灯谱线波长的理论和实验验证

彭华雨,范　婷

(石河子大学 理学院，新疆 石河子　832003)



光栅最小偏向角法测量汞灯谱线波长的理论和实验验证

彭华雨,范婷

(石河子大学 理学院，新疆 石河子832003)

通过理论推导，给出了最小偏向角的表达式，测量得到最小偏向角的具体数值.实验结果表明，用最小偏向角法测量的波长较对称法更准确，另外，光栅常数也是影响实验误差的原因.

最小偏向角；光栅衍射；谱线波长

衍射光栅是由大量等间距狭缝组成的集合体.当一束平行光垂直入射衍射光栅时(如图1)，光波在各狭缝处发生衍射，据光栅方程可知，衍射条纹的主极大位置：

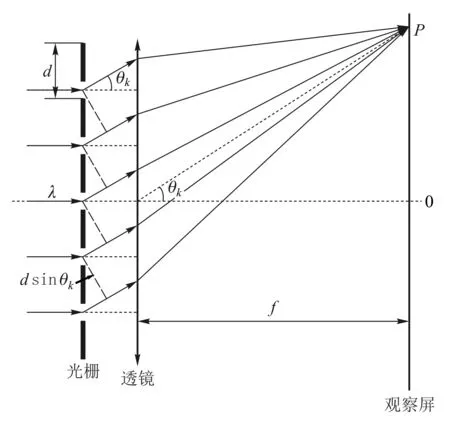
图1　衍射光栅垂直入射示意图

(1)

其中d为光栅常数，θk为第k级衍射明纹所对应的衍射角，λ为入射光波波长.

当一束平行光以一定角度射入光栅时(如图2)，光栅方程则为

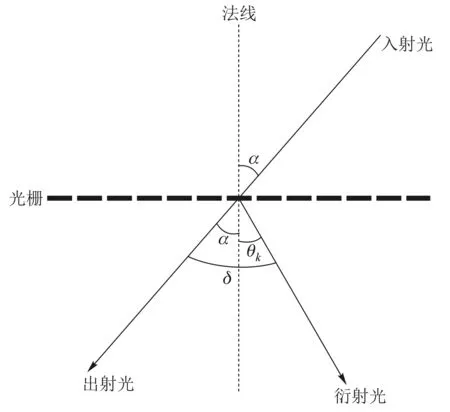
图2　衍射光栅斜入射示意图

d(sinθk±sinα)=kλ,(k=0,±1,±2,…)

(2)

1　理论证明最小偏向角的存在

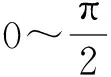
最小偏向角存在的两个条件[1,2]：

(3)

(4)

式(3)给出

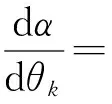
(5)

式(2)给出

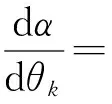
(6)

(7)

正负号一一对应，式(7)简化为cosθk=cosα

(8)

当θk=α，θk和α处于法线的同一侧，最小偏向角δ=2α；

当θk=-α，θk和α处于法线的异侧，即入射光线与衍射光线重合，δ=0，显然这是中央明纹的位置，不是最小偏向角的位置.

以上是由式(2)和(3)推出最小偏向角δ=2α，下面验证结果对于式(4)是否成立.

式(2)中

(9)

对式(9)求关于θk的二阶导数

(10)

将式(9)代入式(10)，得到

(11)

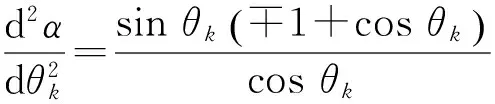
1+cosθk>0

(12)

-1+cosθk>0

(13)

显然式(12)成立，而式(13)不成立.式(13)中的负号对应式(2)光栅方程中的负号，即衍射光线与入射光线位于法线异侧的情况，该式的不成立说明了最小偏向角只能在入射光线的法线的同侧位置，这也证明了按照条件(3)得到的δ=0是不成立的.

通过以上证明，当一束单色平行光斜入射到衍射光栅上时，衍射光线与入射光线之间存在最小的偏向角，且最小偏向角只有一个，此时衍射光线位于入射光线的法线同侧，大小δ=2α.此时光栅方程就可以写成：

(14)

式(14)是求入射谱线波长的基本公式，关键在于测量最小偏向角δ.

2　利用最小偏向角法测量汞灯入射光波长

2.1确定最小偏向角位置

实验用的仪器包括：分光计、300条/mm透射光栅、600条/mm透射光栅、汞灯.找到最小偏向角的位置是实验的关键，可以分为4步：1) 调节分光计；2) 将光栅放在载物台上，使光栅平面和光栅刻痕平行于载物台的转轴；3) 打开汞灯，待光源稳定后，通过目镜观察衍射明纹，确保可以观察到第三级，并且明纹在一条水平线上；4) 改变入射角，则谱线将随之移动，当某一条谱线与零级偏离最小时，即可由该谱线与零级谱线的方位测出相应的最小偏向角δ[2].不同谱线的δ值是不同的.

2.2实验结果

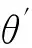
2.3实验分析

1) 实验证实最小偏向角的存在，可通过最小偏向角测量光波波长；

2) 对于300条/mm的光栅，级数不同误差也不同，第一级的误差最小，满足误差随级数的增加而增大；

3) 相比300条/mm的光栅，600条/mm光栅的实验误差更大，这是由于600条/mm光栅观察的谱线光强较弱，所以选择300条/mm光栅即可满足实验需要.

4) 对比相同的谱线，发现对称法的误差比最小偏向角法的误差大；但是通过对左右谱线测量结果进行平均(对称法第一级平均之后的误差为0.102%)，误差可以减小，但相比最小偏向角法仍然大了些.

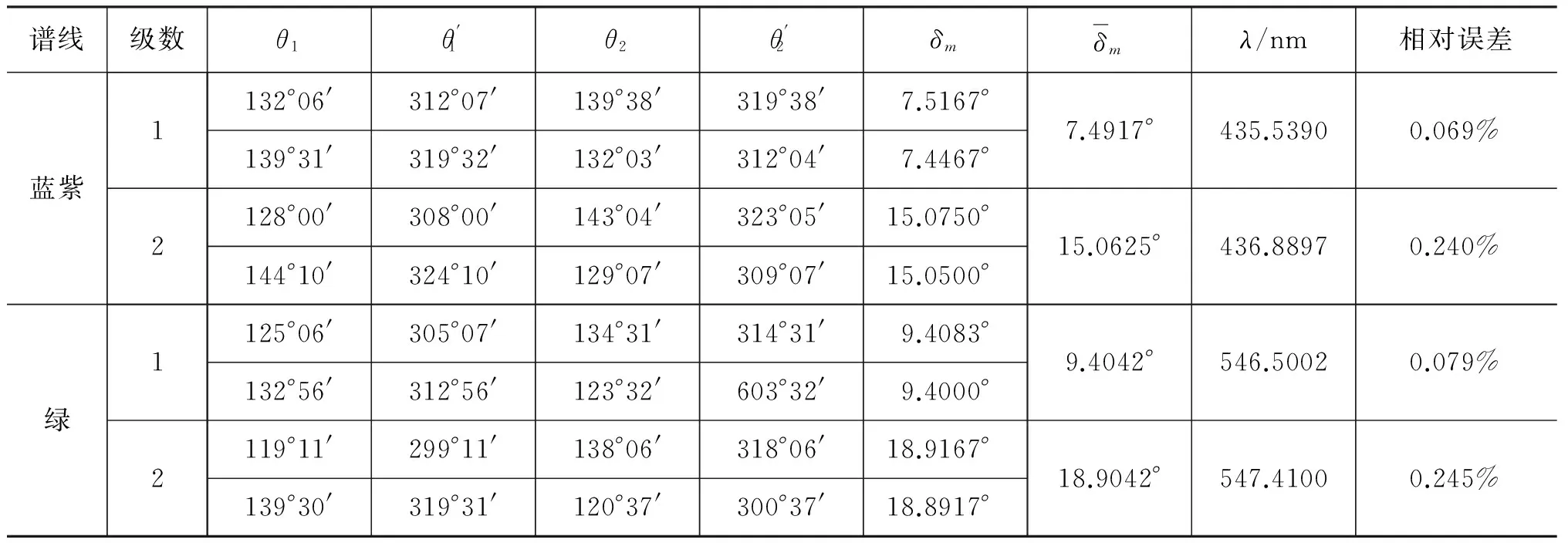
表1　300条/mm光栅最小偏向角法实验测量结果

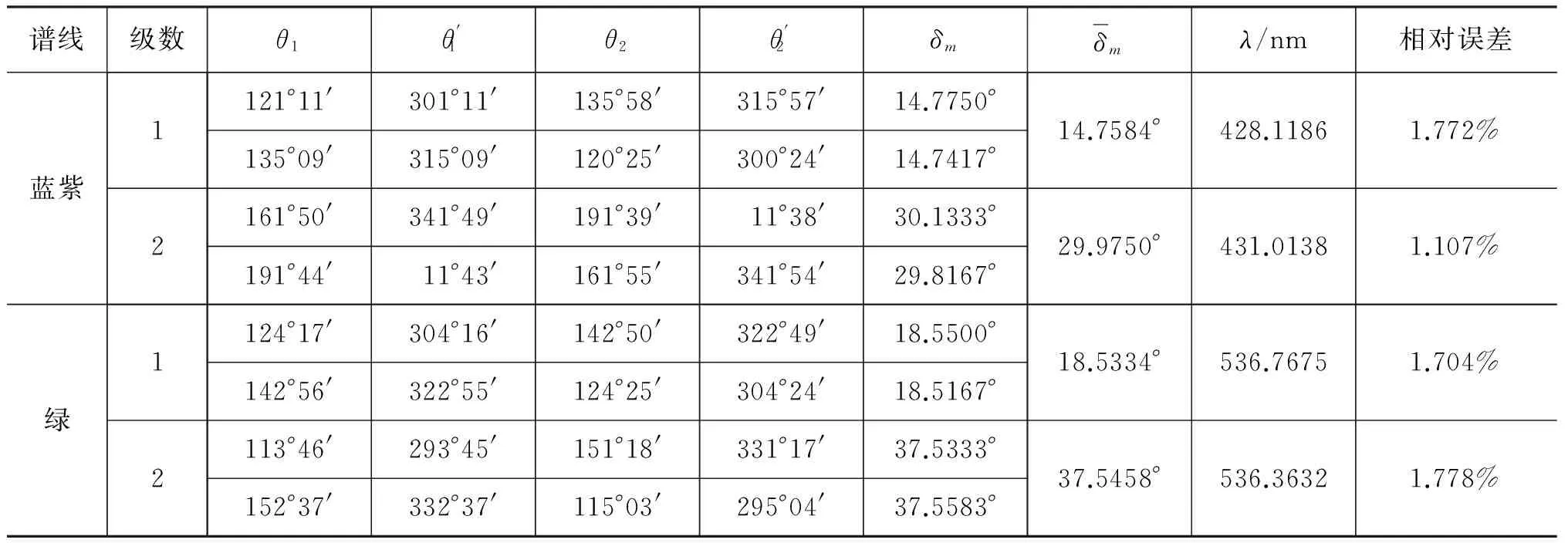
表2　600条/mm光栅最小偏向角法实验测量结果

表3　300条/mm光栅对称法实验测量结果(435.84 nm蓝紫光)

3　结论

使用简单的求导方法，在光栅方程的基础上验证并推导出了最小偏向角和最小偏向角测量波长的公式.利用最小偏向角法，分别使用300条/mm和600条/mm的光栅测量了汞灯的蓝紫和绿光的波长，验证了此方法的可行性，并通过对比对称法的实验数据，表明最小偏向角法相比对称法误差更小.从实验数据总结得到，此实验选用300条/mm的光栅非常合适，误差在0.3%以内.测量的蓝紫光波长比绿光波长更准确，适合测量级数较低的谱线波长.

对比对称法，最小偏向角法的缺点是追踪到最小偏向角的位置相比对称法麻烦了一些.

对比对称法，最小偏向角法的优点有以下3方面：

1) 需要测量的数据少，误差更小.由最小偏向角的方法原理可以知，只需要测出最小偏向角的位置，不需要测量左右两条对称谱线来减小误差，不需要入射光波与光栅平面垂直，且波长的获得与斜入射角α无关,消除了对称法由α所引起的误差.

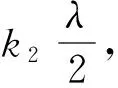
3) 衍射现象更为明显.理论和实验都可以证明，最小偏向角法观察到的同级明纹的光强比对称法的同级光强要强，更易于观察[4].

[1]王宏明.再议用最小偏向角测光波波长的实验原理[J].大学物理实验，1997,3(10):26-27.

[2]吴粟英.一种用光栅测定光波波长的方法[J].物理实验，1983(6):253-254.

[3]薛新英,彭桂兰.利用最小偏向角法测定光的波长[J].塔里木农垦大学学报，2000,3(12):40.

[4]姚启钧.光学教程[M].北京：高等教育出版社，1989：223-237.

Theory and experimental verification of measuring mercury lamp wavelength by the grating least deviation angle method

PENG Hua-yu, FAN Ting

(College of Sciences，Shihezi University，Shihezi, Xinjiang 832000，China)

Through theoretical derivation, the expression of the minimum deviation angle is given. We get the accurate values of the minimum deviation angle by measure. The experimental results show that the measurement is more accurate than symmetry method. The results also show that the grating constant is one of the reasons of the experimental error.

least deviation angle; grating diffraction; line wavelength

2015-05-05；

2015-10-12

石河子大学教改项目(JG-2012-028)资助

彭华雨，(1994—)，男，江苏连云港人，石河子大学理学院应用物理学专业2012级本科生.

范婷，E-mail:ft_tea@shzu.edu.cn

O 436.1

A

1000- 0712(2016)02- 0056- 04