极性分子晶体的振动模式及其频谱结构

周艳丽

(国防科技大学 理学院，湖南 长沙　410073)



极性分子晶体的振动模式及其频谱结构

周艳丽

(国防科技大学 理学院，湖南 长沙410073)

讨论了一维极性分子晶体晶格运动的简正模式与频谱结构，分别针对一维均匀和非均匀晶体链给出了理论计算方法以及数值计算结果，并对计算结果进行了详细的讨论与分析.

简正模式；极性分子；一维非均匀晶体；一维均匀晶体；模式频率

在固体物理、理论物理以及大学物理等多门物理学课程中，简正模式是一个很重要的概念[1-3]. 它是人们在考虑两个或多个耦合振子的运动时引入的.我们知道，对于一个具有多个运动自由度的复杂系统来说，其一般运动表现非常复杂，因为没有一个部分的运动是简谐运动.但是，如果其运动方程是线性的，则该体系的最一般运动就是多个同时发生的独立的简谐运动的叠加. 我们把这些独立的简谐运动称为简正模式，简称为模式[3-5]. 简正模式就像一个“扩展”的谐振子，它的所有组成部分都以相同的频率和相位振动.

大多数大学物理教材一般只对少体耦合系统如耦合摆，以及连续体系如绳子等宏观物理系统的简正模式进行了较详细的讲解. 其实除了宏观物理系统，微观量子系统的一般微扰运动也可以写成它的所有各个模式的叠加，每个模式的振幅和相位都由初始条件决定. 本文针对极性分子晶体这样一种量子系统[6-8]，来讨论它的简正模式以及频谱结构，并详细地给出了理论计算方法和数值计算结果，这对我们更形象直观地理解微观量子系统的运动情况是有意义的.

极性分子又称有极分子.由于其正电荷系的中心与负电荷系的中心不重合[9]，极性分子具有內禀电偶极矩，所以极性分子之间存在偶极-偶极相互作用[10].人们已经证明，在低温情况下，极性分子的正负电荷中心会在电场的作用下发生转动，以期顺着外电场的方向，即偶极矩的排列变得有秩序了，有序的极性分子会因相排斥的偶极-偶极相互作用而形成一种稳定结构[6].在这种状况下，如果极性分子运动的动能小于其受到的势能，每个分子将会在其平衡位置附近做相互关联的微扰运动，我们称这种状态为晶体相[10].晶体中各个分子之间的这种相互关联的微扰运动就可以用集体振动模式——简正模式来描述. 在低温条件下，晶体中的分子运动即晶格运动可以量子化，其中每种简正模式的能量量子就是声子，声子的频率就等于简正模式的频率[10].

为了形成分子晶体，除了极低温之外，还需要外加囚禁势将分子限制在有限范围内，以保证分子在平衡位置附近作微扰运动. 在理论研究方面，比较具有代表性的是一维均匀分子晶体和一维非均匀分子晶体，在实验上这两种晶体结构分别可以通过施加弱囚禁势和谐势阱来产生[10]. 关于这种晶体相的研究，不仅涉及到凝聚态物理、原子分子物理等领域，甚至也是近期非常热门的量子操控、量子模拟等方向的研究重点[11-14]. 在文献[15]中，作者研究了一维量子系统——离子晶体链的晶格运动和频谱结构. 与离子之间的相互作用是距离平方反比的库仑力不同，极性分子之间是距离4次方反比的偶极-偶极力. 本文将针对一维分子晶体链展开讨论，分别研究非均匀与均匀一维晶体的简正模式与模式的频谱结构，讨论分子个数对频谱结构的影响，以及两种晶体结构之间的差异.

1　一维非均匀晶体

考虑一个三维谐势阱，其径向囚禁频率远大于轴向囚禁频率，这样极性分子的径向运动将会大大地受到限制，从而沿着轴向排成线，故将这种结构称之为一维分子链.在讨论其运动时，可近似认为径向运动被冻结，故在本文我们只讨论轴向(纵向)运动.在轴向囚禁频率为ν的谐势阱中，极性分子所受到的总势能为[7-8,10-11]

(1)

其中xi为分子i在轴向的动量和位置坐标分量，m是分子的质量，ν是阱的轴向囚禁频率，μ0是极性分子的电偶极矩. 上式中第一项为势阱提供的势能，第二项为分子之间的偶极-偶极相互作用. 如果温度足够低，各个分子将会在平衡位置附近作微扰运动，即

(2)

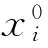
分子的平衡位置由下式决定

(3)

(4)

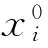
将总势能V在平衡位置处展开到二阶并忽略更高阶项，得

由于矩阵Bij是实的非负对称矩阵，它的本征值应该大于0，且满足本征值方程：

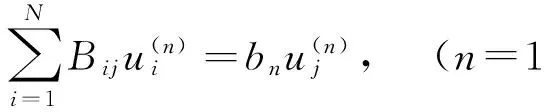
(6)

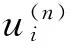
(7)

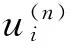
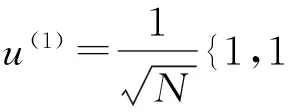
(8)

(9)

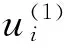
表2　分子数N=2～10时矩阵Bij的本征值和对应的本征矢

定义简正坐标与简正动量：

(10)

系统的哈密顿量可以表示为

(11)

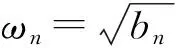
图1　N=2～4时一维分子链的(纵向)振动模式.具有N个分子的一维分子链有N种模式.箭头的方向表明各分子偏离平衡位置时振动的方向，箭头的(相对)长短表明各分子的振幅大小

分析表2容易得出：

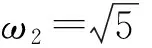
2) 对于第n阶模式(除了质心模和呼吸模)来说，其频率随着N的增大而会微弱地减小. 比如N=4时第4阶模式的频率ω4=4.82ν，N=5时的第4阶模式频率ω4=4.79ν，二者相差很小；这是因为N越大分子之间的间距慢慢减小，导致相对运动的幅度减小，这样分子需要的回复力减小，所以模式频率会稍微变小.

3) 模式频率随着模式阶数n的增大而增大. 其原因是，随着n的增大，越多的相邻分子对开始反步调地振动——也就是对应的驻波节点越多，并且相对位移增大，这就意味着分子所需要的单位位移的回复力将增大，所以模式频率随着n增大. 由于在谐势阱中极性分子所受的势能不均匀，各相邻分子的平衡位置的间距不相等，且受分子数的影响，所以很难给出高阶频谱的解析形式[15]. 但是考虑到分子数N对各阶频率的影响不明显，根据数值结果，可以拟合出高阶模式的频谱表达式：

(12)

图2给出了N=15时，各阶模式频率的大小，其中离散点给出数值计算的结果，线状给出的是拟合表达式(12)的结果. 可以看到ωn几乎随着模式阶数n线性增大，且对高阶模式来说，频谱可近似写为线性表达式ωn=ν1.22n[10].

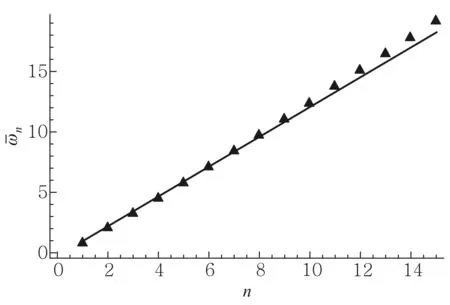
图2　N=15时，一维非均匀分子晶体的频谱结构，其中点状给出的是数值计算的结果，线状给出的是拟合式(12)的结果

2　一维均匀晶体

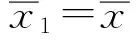
(13)

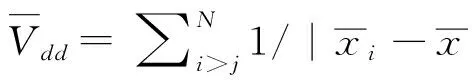
(14)

得到

(15)

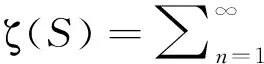
(16)

(17)

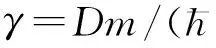
图3给出了各阶模式的无量纲频谱随阶数n的变化情况. 与图2进行对比，可以看到:

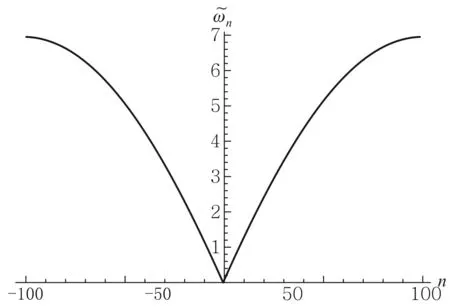
图3　N=100时，一维均匀分子晶体的各阶振动模式的频谱结构

1) 同于谐势阱中n∈[1,N]，这里n∈[-N/2,N/2]，且相同的|n|具有相同的能量；即能量是简并的；

2) 谐势阱中模式频率随n的变化几乎是线性的，而这里则是存在最大值，且该最大值与分子数N无关，人们一般将之称为德拜频率

(18)

但是值得注意的是，当n<

3) 在谐势阱中模式频率最小值为囚禁势频率，而这里模式最小频率为零. 这是因为在谐势阱中分子总会受到外加的囚禁势所产生的回复力的作用，而在一维均匀晶体链情况下该外加的回复力近似为零.

3　结束语

本文讨论了一维极性分子晶体链的简正振动模式和频谱结构，并分别对一维均匀晶体链和一维非均匀晶体链这两种情况给出了详细的理论计算方法和数值计算结果. 对一维非均匀晶体，我们给出了数值计算结果和频谱的拟合公式，结果表明，其振动模式的频率随着阶数n几乎成线性变化，但是依赖于分子总数N；而对于一维均匀晶体的振动模式和频率结构，我们给出了解析形式，结果表明，其振动模式的频率存在最大值且不依赖于N，但是对低阶模式来说，其频谱随阶数可近似看作线性变化.

[1]黄昆,韩汝琦.固体物理学[M]. 北京：高等教育出版社, 1998.

[2]刘年寿. 理论物理基础教程[M]. 北京: 高等教育出版社，2008.

[3]张三慧. 大学物理学：热学、光学、量子物理[M]. 3版.北京：清华大学出版社，2009.

[4]李承祖，杨丽佳. 大学物理学(下册)[M]北京：科学出版社，2009.

[5]F. S.克劳福德[美]. 伯克利物理学教程 (3卷上册)[M]. 北京：科学出版社，1981.

[6]Pupillo G, Micheli A, Büchler H P, et al. Cold Molecules: Creation and Applications[M]. Boca Raton: CRC Press, 2009.

[7]Pupillo G, Griessner A, Micheli A, et al. Cold Atoms and Molecules in Self-Assembled Dipolar Lattices[J]. Physical Review Letters, 2008, 100(5):050402.

[8]Micheli A, Brennen G K, Zoller P. A toolbox for lattice-spin models with polar molecules[J]. Nature Physics, 2006, 2:341.

[9]徐龙道,等. 物理学词典[M]. 北京: 科学出版社,2007.

[10]Rabl P, Zoller P. Molecular dipolar crystals as high-fidelity quantum memory for hybrid quantum computing[J]. Phys Rev A, 2007, 76: 042308.

[11]Zhou Y L, Ortner M, Rabl P. Long-range and frustrated spin-spin interactions in crystals of cold polar molecules[J]. Phys Rev A, 2011, 84: 052332.

[12]Syzranov S V, Wall M L, Gurarie V. Rey AM. Spin-orbital dynamics in a system of polar molecules[J]. Nature Communication, 2014, 5: 5391.

[13]Zhou Y L, Ou B Q, Wu W. Quantum simulating the frustrated Heisenberg model in a molecular dipolar crystal[J]. Physics Letters A, 2015, 379: 2569-76.

[14]Wen W, Wu W, Zhou Y L, et al. Energy-level structure of ion cloud and crystal in a linear Paul trap[J]. New J Physics, 2014, 16: 083041.

[15]James D F V.Quantum dynamics of cold trapped ions with application to quantum computation[J]. Applied Physics B, 1998, 66: 181-90.

The normal modes and the energy spectrums of molecular dipolar crystals

ZHOU Yan-li

(College of Science, National University of Defense Technology, Changsha, Hunan 410073, China)

The normal modes and phonon spectrums of an ensemble of polar molecules are discussed, which are prepared in a dipolar crystalline phase. Detailed results are presented for a one-dimensional dipolar chain trapped in harmonic trap and for a homogeneous dipolar crystal, respectively.

normal modes; polar molecules; homogeneous dipolar crystal in 1D; harmonically confined dipolar crystal in 1D; phonon spectrum

2015-08-25；

2015-12-02

国家自然科学基金项目(11304390)资助

周艳丽(1981—)，女，湖北宜城人，国防科技大学讲师，博士，主要从事量子信息、量子光学的研究工作以及大学物理教学工作.

O 481

A

1000- 0712(2016)07- 0017- 07