大坝实测变形差值统计分析

王建学，李　民,曹学兴

(1.广东省水利电力勘测设计研究院，广州 510635；2.武汉大学 水利水电学院，武汉 430072；3.华能澜沧江水电股份有限公司，昆明 650214)



大坝实测变形差值统计分析

王建学1，李民2，*,曹学兴3

(1.广东省水利电力勘测设计研究院，广州 510635；2.武汉大学 水利水电学院，武汉 430072；3.华能澜沧江水电股份有限公司，昆明 650214)

环境量因子之间存在的相关性直接影响大坝安全监测统计分析的结果。基于某混凝土拱坝实测变形资料，采用差值统计分析方法对因子间的相关影响进行消除，并与常规逐步回归分析方法进行了对比。结果表明，差值统计分析在自动化监测采集条件下可达到逐步回归的精度并保证统计分析的可靠性。

相关性；大坝；变形；差值统计分析

混凝土坝在各种环境因素的作用下会产生变形、应力以及渗流等效应，它们反映了大坝的结构性态[1]。大坝安全监测就是要根据监测资料建立有关效应量与环境量之间的关系，以此来反映相应环境量对大坝效应量的影响程度，并据此关系是否符合一般规律来判断其性态是否正常。大坝变形是容易且必须监测的一个主要效应量，通过变形性态来反映大坝的实际工作性态，并作为判断其是否正常的依据。

建立大坝变形效应监测量与相应环境量之间的关系一般通过建立统计模型来实现，但在统计分析中，由于上游水位与坝址气温等环境因素之间往往存在相关性，从而影响统计回归分析的结果[2]。对于统计回归分析中因子间的相关影响是一个有待于解决的难题[3-7]，但针对一个具体工程变形效应量的分析，可以结合实际情况，在统计分析过程中尽可能避免或通过适当的取值方式消除环境量之间的相关影响来保证统计分析成果的可靠性[8-10]。本文针对某混凝土拱坝变形效应量采用差值统计分析来消除环境量之间的相关影响。

1　工程概况

某水库拦河大坝为三心双曲变厚混凝土拱坝，最大坝高102 m，坝顶高程194 m，坝顶弧长350.6 m，坝顶厚5 m，底部最大厚度24.6 m，厚高比0.24，共分为20个坝段。泄水建筑物为2对中、浅泄水孔，其中1对泄水浅孔布置在2#和15#坝段中线上，另1对泄水中孔则分别布置在6#和14#坝段中心线上。

为监测大坝的变形情况，在各坝段坝顶设有前方交会监测点，在拱冠11#坝段、左岸4#坝段、左1/4拱弧的7#坝段、右1/4拱弧的13#坝段和右岸17#坝段各设1组正倒垂线监测坝体挠度情况。变形监测设施在下闸蓄水前已投入使用，之后具有完整的监测数据系列，并在2004年6月对坝体挠度以及相应的环境量实现了监测数据自动化采集。由于该水库属于调节性水库，上游水位变化和相应的坝址气温变化皆具有明显的年周期特点，它们之间存在相关关系的可能性较大。为确定变形与相应环境量之间的统计关系，最好消除上游水位与坝址气温的相关影响。为此对该混凝土拱坝变形监测数据采取差值统计分析方法。

2　差值统计分析

该拱坝变形效应监测量δ通过建立统计分析模型后一般可以表示为各环境影响分量之和，即：

(1)

式中δW为水压分量；δT为温度分量；δτ为时效分量；a0为常数项。

式(1)又可以表示为以下形式：

(2)

式中m1、m2、m3分别为水压因子、温度因子和时效因子的个数；H为坝前水深或水位值；Ti为第i个温度因子；τi为第i个时效因子；bi、ci、di分别为第i个水压因子、温度因子和时效因子前的回归系数。

差值统计计算的基本思路是选取某一环境量作用相同条件下的一系列(n1次)效应量监测值代入式(2)，于是得到n1个效应量测值以及相应的方程，各方程中那个具有相同作用条件的环境影响分量值都是一样的，将它们适当相减即可消除该环境影响分量而得到n1-1个差值方程式，由此通过回归分析可确定余下环境影响分量，然后再建立剩余效应量与相应环境量之间的统计关系，两者结合共同描述大坝监测效应量与相应环境量之间的关系。

2.1等水位位移差值统计模型

给定一上游水位H1，在效应量实测系列中找到k1个效应量值δti(i=1,2,…,k1)，也即：

(3)

式中ti时刻的位移值、温度值的取值在测次较疏时(人工观测)采用线性插值获得，在测次较密时(自动化监测)则可直接读取。

由式(3)，将δt2、δt3、…、δtk1减去δt1，得k1-1个差分方程：

(4)

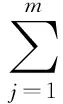
(5)

2.2剩余位移与水位相关的统计模型

将对应上游水位为H1、H2、H3、…、Hm时刻的总效应量测值δi(i=1,2,…,m)减掉由式(5)确定的温度及时效环境分量值δT,τi(i=1,2,…,m)，得到剩余位移值δWi(i=1,2,…,m)，再对其进行逐步回归分析确定剩余位移值与上游水位的关系：

(6)

2.3位移总模型

最后得到最终模型为：

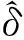
(7)

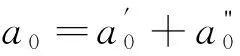
3　大坝实测位移差值统计分析计算

对该混凝土拱坝拱冠梁11#坝段坝顶194 m高程径向水平位移监测值进行差值统计分析，选取2004年11月22日至2008年10月31日每天9:00时的测值共1 424个位移值作为样本数据。

1)选取在相同水位下的位移监测值。编制计算机程序，认为变化在±0.1 m范围内的水位是相同水位，由此选取130个位移值。

2)构造温度和时效因子形式。时效分量选取ln(1+t)、1-e-t和t因子得线性组合形式，其中t是当次观测日相对首次观测日的日序值；温度分量选取T0-1、T2-15、T16-30、T31-60、T61-90、T91-120因子的线性组合形式，其中Ti-j表示观测日前i至前j天的日平均气温值。

3)计算位移差值。由式(4)计算相应的129组位移差值。

4)建立消除水压后的位移统计分析模型。以上述9个因子为待选因子，根据129组位移差值，通过逐步回归建立相应的回归模型：

0.087 960 02T0-1+0.367 951 602T2-15+0.174 623 396T16-30+0.292 625 576T31-60+

0.538 691 58T61-90+0.377 594 888T91-120

(8)

其复相关系数R为0.983；剩余标准差S为2.037 mm。

(9)

6)综合式(8)和式(9)，得到位移差值统计总模型如下:

0.087 960 02T0-1+0.367 951 602T2-15+0.174 623 396T16-30+

0.292 625 576T31-60+0.538 691 58T61-90+0.377 594 888T91-120-

0.551 613ln(1+t)+8.288 851 738(1-e-t)+0.001 397 434t

(10)

7)差值统计分析与常规逐步回归分析成果比较。由常规逐步回归分析得到该拱坝11坝段坝顶194 m 高程挠度回归方程为:

0.001 676 526t-3.653 494×10-8H4+0.109 686 9T0-1+0.293 536T2-15+

0.203 885 9T16-30+0.421 304 2T31-60+0.368 818 7T61-90+0.397 158 6T91-120

(11)

复相关系数R为0.996，剩余标准差S为0.814 mm。

实测位移值、逐步回归拟合值和差值统计拟合值过程线见图1。

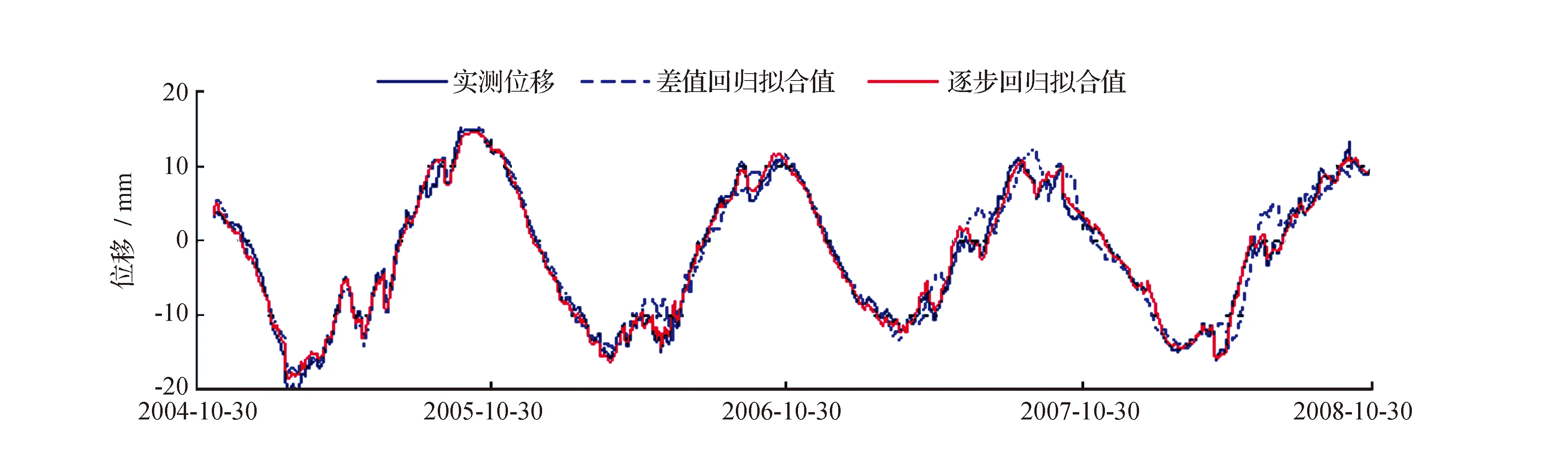
图1　实测位移值、逐步回归拟合值和差值统计拟合值过程线Fig.1　Process line of measured deformation,stepwise regression fitted values and difference statistical fitted values

由对实测位移的拟合情况可见，两者的复相关系数皆在0.9以上，逐步回归方法高于差值统计方法。从原理上来说，为消除密切相关的因子对回归的影响，差值统计是有效的，但由于建模过程中多了差值计算、剩余位移值计算等环节，增大了误差，还有用于差值统计的差值数据量仅129个远小于用于逐步回归的1 424个，此为一重要原因。

为解决此问题，须增加相同水位条件下的位移值。在仅具有人工观测条件的情况下效果无法达到最佳，因为增加测值就是要增加插值，但在具备自动化监测的条件下会有一定效果，因为在此种条件下数据采集频率通过人为进行设置，可达到1次/10 min甚至更高。

差值统计分析的长处在于分离各环境影响分量上，由于消除了环境量因子间的相关性影响，由差值统计分析确定的各环境影响分量更为准确。当然要保证这一点，先要解决好整体拟合精度问题。

4　结　论

在大坝安全监测统计分析中，由于环境量因子间密切相关的影响，难以准确地从大坝实测效应量中分离出各环境影响分量。采用差值统计分析大坝实测位移可有效地消除环境量因子间密切相关的影响，从而保证相应环境影响分量分解的质量。在现有自动化采集监测数据的条件下，差值统计分析方法不仅能够达到与常规逐步回归分析相当的精度，更主要的是由于消除了环境因子间相关影响，所得到的统计分析成果更为可靠。

[1]李珍照.混凝土坝观测资料分析[M].北京:水利电力出版社,1989.

[2]杨晓灵,朱建.差值逐步回归法新方法[J].水电自动化与大坝监测,1989(1):10-14.

[3]赵松山.对多重共线性的深入思考[J].当代财经,2003(6) :125-128.

[4]王玉梅.多重共线性的消除:不相关法[J].统计教育,2006(7):18-19.

[5]鲁茂,贺昌政.对多重共线性问题的探讨[J].理论新探,2007(8):6-9.

[6]刘琼,多重共线性的程序选优法[J].学术研讨,2008(11):393-394.

[7]肖雪梦，张应应.三种回归方法在消除多重共线性及预测结果的比较[J].统计与决策，2015(24)：75-78.

[8]周祖权.天荒坪抽水蓄能电站上库廊道渗水观测回归分析[J].华东电力,2002(5):1-4.

[9]李海枫，张国新，周景秋.特高拱坝施工及初次蓄水期变形回归模型研究[J].水利水电技术，2015，46(1)：70-74.

[10] 曹苏娜,王素云,曹贻鹏.一种新的多元回归思路-因子与回归联合分析法[J].西安文理学院学报：自然科学版,2010,13(2):39-43.

Statistical analysis of difference methods on the measured deformation of the dam

WANG Jian-Xue1，LI Min2，*，CAO Xue-Xing3

(1.GuangdongHydropowerPlanningandDesignInstitue,Guangzhou510635,China；2.SchoolofWaterResourcesandHydropower,WuhanUniversity,Wuhan430072,China;3.HuanengLancangRiverHydropowerInc.,Kunming650214,China)

The existence of correlation among environment factors affects the result of dam safety monitoring statistical data analysis. Basing on a arch concrete dam measured deformation data, statistical analysis of the difference methods is used to eliminate the correlation among impact factors, and the conventional stepwise regression analysis methods are compared. The result shows that statistical analysis of the difference methods can achieve the precision of stepwise regression statistical analysis under the automated monitoring acquisition conditions, while guaranteeing the reliability of statistical analysis.

correlation；dam；deformation；statistical analysis of difference

10.13524/j.2095-008x.2016.03.036

2016-04-22

国家科技计划支撑项目(2013BAB06B01)

TV698.11

A

2095-008X(2016)03-0020-05

王建学(1986-)，男(回族)，河北承德人，工程师，硕士，研究方向：水工建筑物安全监测，E-mail:wangxihao1986@163.com；*通讯作者：李民(1961-)，男，浙江衢州人，副教授，博士，研究方向：大坝安全监测，E-mail:mili613@126.com。

网络出版地址：http:www.cnki.net/kcms/detail/23.1566.T.20160719.1132.004.html