基于模糊聚类的峰谷时段划分
2016-10-15成田宇陈一怀
郑 成田 宇陈一怀
(1. 西华大学电气与电子信息学院,成都 610039;2. 四川省资阳市电力公司,四川 资阳 641300)
基于模糊聚类的峰谷时段划分
郑 成1田 宇1陈一怀2
(1. 西华大学电气与电子信息学院,成都 610039;2. 四川省资阳市电力公司,四川 资阳 641300)
本文根据半梯形隶属函数,采用基于模糊聚类的方法对峰谷时段进行划分调整,并兼顾了系统负荷曲线本身的峰谷形态特征和用户侧的相应需求。通过四川某地的夏季和冬季日负荷数据的算例验证分析表明,该方法可以有效的进行峰谷时段划分,能够为后续实施峰谷分时电价提供参考依据。
分时电价;峰谷时段划分;隶属函数;模糊聚类
目前国内外普遍采用需求侧管理(Demand Side Management)来缓解电力紧张局面,其中峰谷分时电价政策作为有效反映电力系统不同时段供电成本差别的电价机制,也在我国逐步推广使用[1-3]。如何合理的进行峰谷时段的划分则成为分时电价实施的重要基础。
针对峰谷时段划分的理论研究并不多,主要分为以下3个方法[4]:基于隶属度函数的峰谷时段划分、基于供电成本的峰谷时段划分、基于因素分析法的峰谷时段划分。其中,采用隶属度函数的峰谷时段划分方法,是基于定性分析用户负荷侧曲线,更能够体现出峰谷分时电价在用户需求响应中的价格杠杆作用。采用模糊聚类的方法能合理的针对负荷曲线分布特征进行时段划分,也能为后续进一步根据实际情况进行修正提供指导[5]。
1 模糊聚类在时段划分应用中的基本原理
模糊数学的基本思想在于确定研究对象的隶属程度,研究对象的隶属程度存在过渡阶段,不会由一个极端跳跃到另一个极端,这是隶属度具有客观规律,不能主管捏造。聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。隶属度函数是模糊聚类分析的一种方法,主要用于将类型和性质相同的部分归类。
图1为典型日负荷曲线[6],可见该负荷曲线具有双峰特性。
由图 1可见:A点为日负荷曲线中谷负荷,C点为峰负荷,B点为另一个峰值。而其他点却无法清楚的确定是否为峰谷点,只能引入模糊数学的概念对其可能性进行判断,即某点有多大的可能性属于某个时段。而结合负荷曲线分布利用模糊判断确定峰平谷时段中各时段位于峰时段和谷时段的可能性大小时,要注意以下两项原则:①日负荷曲线上最小值一定位于谷时段,不可能处于峰时段;②日负荷曲线上最大值一定位于峰时段,不可能处于谷时段。
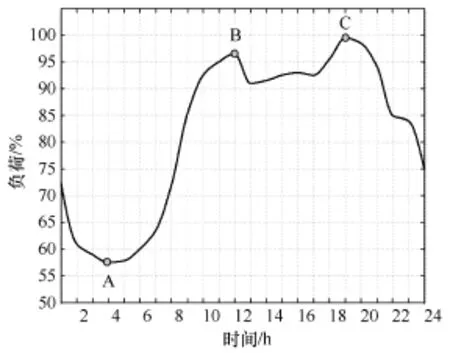
图1 典型日负荷曲线
所以,本文将一天24h内负荷分为峰时刻、平时刻、谷时刻三个时段,分别为Tt、Tm、Tb,Tt+Tm+ Tb=24,通过模糊聚类的方法对24个时间点进行峰平谷时段的划分。对于其他非最值点,采用隶属度函数的方法进行确定[7]。文中采用的额峰谷隶属度是为了判断一天 24个时刻的负荷与当日峰负荷和谷负荷的相关性,与这个时刻具体负荷大小无关。因此考虑使用简单的中间部分呈线性结构的半梯形隶属度函数[8],用偏小型半梯形隶属函数确定各个时刻处于谷时段的可能性,用偏大型半梯形隶属函数确定各个时刻与峰时段的可能性。图2为偏大型半梯形分布和偏小型半梯形分布;式(1)、式(2)分别为偏大型和偏小型半梯形的隶属度计算公式。
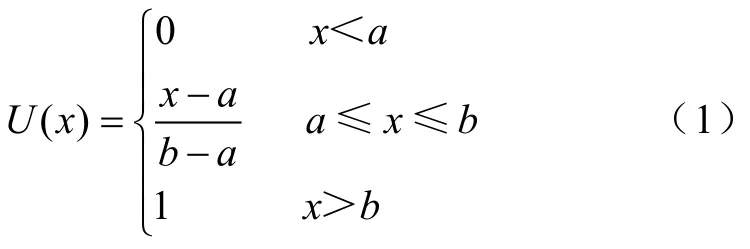

图2 偏大型半梯形分布和偏小型半梯形分布
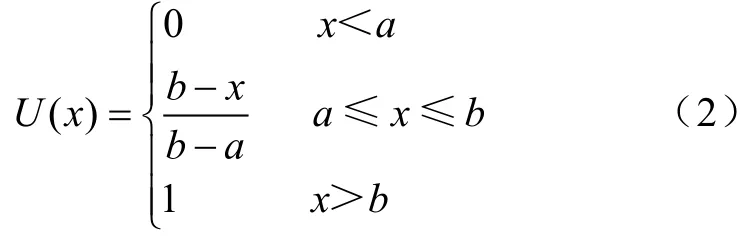
假设日负荷曲线上时间点 T=[T1,T2,…,T24],利用以点盖段的思想,对应的负荷值Pl= [P1(1),P1(2),…, P1(24)]。采用偏大梯形隶属度和偏小型半梯度隶属度函数计算时刻点 Ti(i=1,2,…,24)的峰时段隶属度uti和谷时段隶属度ubi。
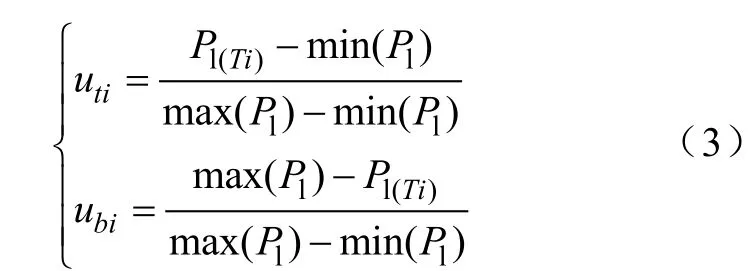
2 模糊聚类在峰谷时段划分中的具体应用
聚类即按照一定规则将特性相同或相似性大的对象划分在一起研究,差异很大的划分到另一类,如此对研究对象进行逐一划分归类。对于研究对象之间存在模糊界限的情况,就需要引入模糊聚类的方法。同理,单一的隶属度函数划分,不能充分确定峰谷时刻,本文引入模糊聚类的方法,根据各时段负荷特性,制定出对应的时段划分规则,从而更为合理的对时段进行峰谷划分。在进行确定峰谷时段划分主要考虑以下三个原则[9]。
(1)要充分考虑各时段用电情况:为方便负荷侧避峰,峰时段不能超过谷时段2h。
(2)要尽可能保持负荷侧的电费支出不出现大幅波动:峰、平、谷三个时段的总时间长度均不能低于6h。
(3)要方便负荷侧调整生产计划:每一个时段长度不应低于2h。
考虑到数据特性,本文主要采用基于模糊等价关系的传递闭包方法,具体过程如下所示[10]。
(1)统计指标选择:本文以各时刻点负荷数据为分类对象,各时刻点的峰、谷隶属度统计指标,有

式中,i=1,2,…,24。则可得到日负荷曲线上各点组成的时刻点集合的特性指标矩阵T:
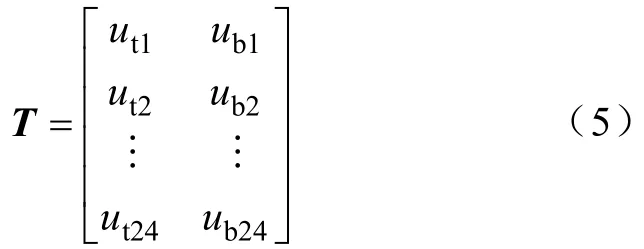
(2)数据标准化处理:采用平移—标准差变化的方法对矩阵T进行处理,具体如下:

(3)建立模糊相似矩阵,建立 ti与 tj的相似关系:依照传统聚类方法确定相似系数,建立模糊相似矩阵,ti与tj的相似程度rij=R(ufi,ugj)。

式中,i=1,2,…,24;j=1,2,…,24;为保证0≤rij≤1,在聚类过程中把c作为约束变量,得到模糊相似矩阵(rij)24×24:

(4)采用模糊传递闭包法,进行聚类:采用平方法求取R的传递包t(R*)。对标定的模糊相似矩阵R依次求取平方,R2=R*R,R4=R2*R2,,经过n次运算后,R2n=Rn*Rn=Rn时,R*=Rn即为传递闭包,有
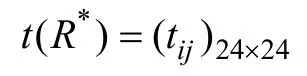


(5)确定阈值λ:最佳模糊聚类分析中对于各个不同的λ∈[0,1],可以得到不同的分类,需要设定一个具体的阈值λ,以确定分类数目。在动态聚类图中,不需要事先估计样本应分成几类,可以令λ 从1开始逐渐减小进行动态聚类,直到聚类数为3,就可得到峰、平、谷时段划分结果[11]。
3 算例分析
选择四川某地的夏季典型日负荷和冬季典型日负荷数据进行基于模糊聚类的峰谷时段划分,具体数据见表1。
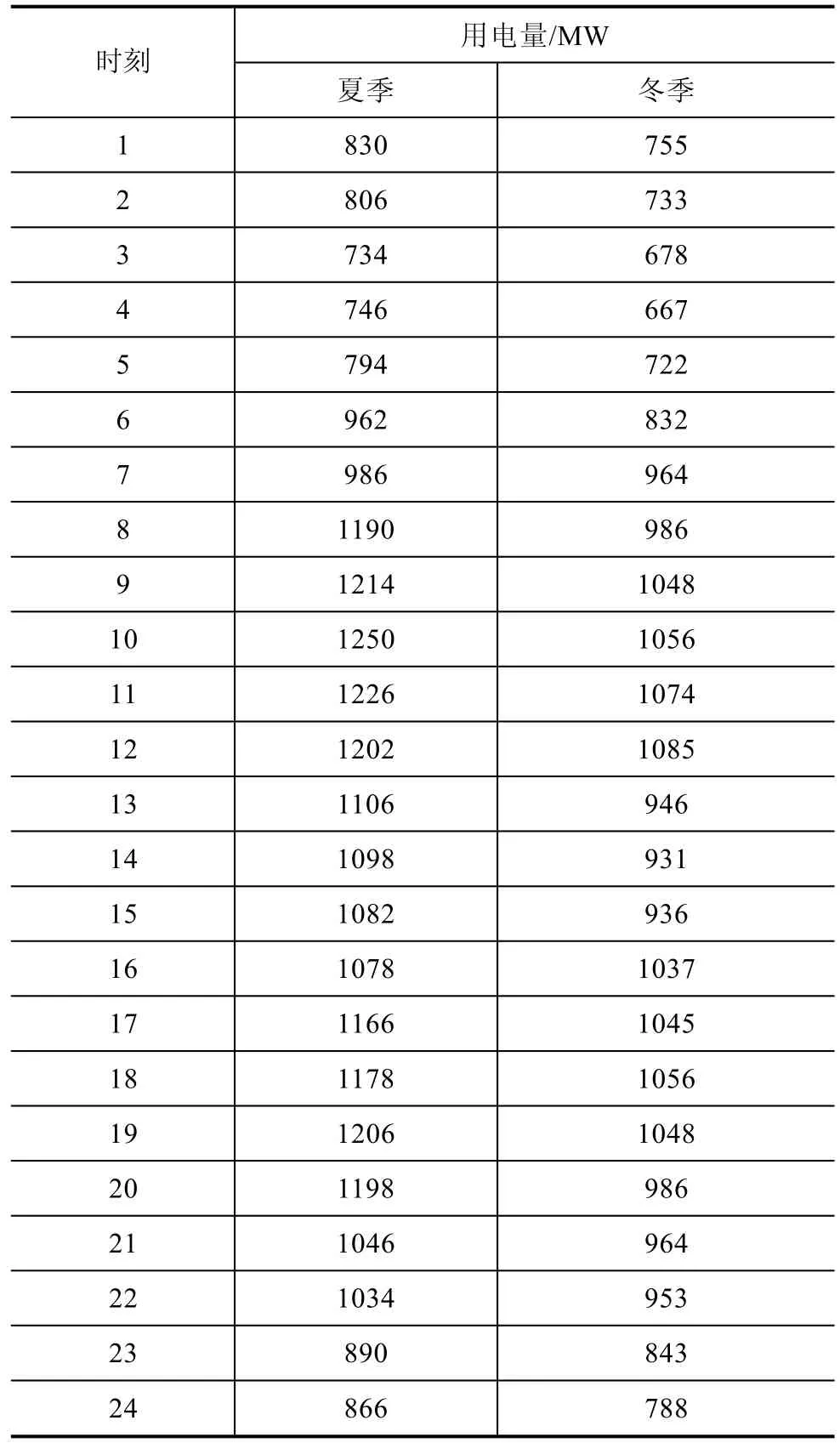
表1 四川某地日负荷数据
根据峰谷时段划分的模糊判断准则,由式(3)得出各时刻点处于谷时段与峰时段的隶属度,见表2。

表2 夏季和冬季各时刻点的峰/谷隶属度
基于表2中各时刻峰、谷隶属度属性值的大小,采用Matlab实现模糊聚类,图3、图4分别给出了夏季和冬季树状聚类图,利用截矩阵进行聚类,当聚类图右侧分类数取3时,得到了峰平谷的时段划分方案。

图3 夏季峰谷时段划分动态聚类图

图4 冬季峰谷时段划分动态聚类图
夏季时段划分:λ由1变到0.8332,如树状聚类图3所示,得到峰谷时段划分方案如图5所示。

图5 夏季日负荷曲线峰平谷划分情况
峰时段 Tf:t8、t9、t10、t11、t12;t17、t18、t19、t20。
平时段Tp:t6、t7;t13、t14、t15、t16;t21、t22。
谷时段Tg:t23、t24;t1、t2、t3、t4、t5。
冬季时段划分:λ由1变到0.8475,如树状聚类图4所示,得到峰谷时段划分方案如图6所示。
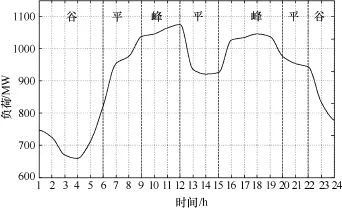
图6 冬季日负荷曲线峰平谷划分情况
峰时段Tf:t10、t11、t12;t16、t17、t18、t19、t20。
平时段Tp:t7、t8、t9;t13、t14、t15;t21、t22。
谷时段Tg:t23、t24;t1、t2、t3、t4、t5、t6。
由图 5、图 6可以看出,将四川某地夏季和冬季日负荷曲线划分成7个时段:2个峰时段、3个平时段、2个谷时段。经检验,夏季某日的峰、平、谷三个时段分别时长为9h、8h、7h,其中最长时段的时长为5h,最短时段的时长为2h;冬季某日的峰、平、谷三个时段分别时长为8h、8h、8h,其中最长时段的时长为6h,最短时段的时长为2h,时段划分情况符合前文所述划分原则。
4 结论
合理划分峰谷时段是后续进行分时电价的基础,本文采用四川某地的夏季典型日负荷和冬季典型日负荷数据,对基于模糊聚类的峰谷时段划分方法进行了验证。结果表明,采用模糊聚类的方法能够迅速准确的反应各时点的峰谷负荷情况,能够为后续添加峰谷分时电价等政策提供有效指导。
[1] 胡兆光, 陈铁成, 纪洪, 等. 在北京地区实施需求侧管理的效益分析[J]. 电力系统自动化, 1999, 23(13): 22-25.
[2] 杨大雄, 陈雁. 上海市峰谷分时电价特性及效益分析[J]. 华东电力, 2005, 33(11): 20-23.
[3] 赵娟, 谭忠富, 李强. 我国峰谷分时电价的状况分析[J]. 现代电力, 2005, 22(2): 82-85.
[4] 李虹, 贾玲. 分时电价峰谷时段划分方法研究[J].中国电业(技术版), 2011(9): 1-3.
[5] 丁宁, 吴军基, 邹云. 基于 DSM 的峰谷时段划分及分时电价研究[J]. 电力系统自动化, 2001, 25(23): 9-12, 16.
[6] 连振洲, 温步瀛, 江岳文. 基于负荷曲线分布特征的峰谷时段划分和修正策略研究[J]. 电网与清洁能源, 2014, 30(7): 15-19.
[7] 胡福年, 汤玉东, 邹云. 需求侧实行峰谷分时电价策略的影响分析[J]. 电工技术学报, 2007, 22(4): 168-174.
[8] 罗伶. 基于模糊c均值聚类的分类分时电价研究[D].济南: 山东大学, 2013.
[9] 范春梅. 梯级水库群短期优化调度研究[D]. 南京:河海大学, 2007.
[10] 曲福恒, 崔广才, 李岩芳, 等. 模糊聚类算法及应用[M]. 北京: 国防工业出版社, 2011.
[11] 翟娜娜. 基于负荷侧响应的峰谷分时电价时段划分[D]. 北京: 华北电力大学, 2011.
Research of Peak and Valley Time Period Partition based on Fuzzy Clustering
Zheng Cheng1Tian Yu1Chen Yihuai2
(1. School of Electrical and Electronic Information Engineerin, Xihua University, Chengdu 610039; 2. Ziyang Electric Power Corporation, Ziyang, Sichuan 641300)
According to semi-trapezoidal membership function, this paper adopts fuzzy clustering method to peak and valley time period partition, and takes into account both the peak-valley morphological features of load curve of power system and the corresponding requirements of users. By analyzing the summer and winter daily load data of somewhere in Sichuan province, it shows that this method can effectively partition peak and valley time periods and provide
for subsequent implementation of peak and valley time price.
time-of-use price; peak and valley time period partition; membership function; fuzzy clustering
郑 成(1989-),男,硕士研究生,研究方向为分布式电源准入。
