激波针气动特性及外形参数优化研究

李永红，高川，唐新武

（中国空气动力研究与发展中心高速空气动力研究所，四川绵阳621000）

激波针气动特性及外形参数优化研究

李永红，高川，唐新武

（中国空气动力研究与发展中心高速空气动力研究所，四川绵阳621000）

采用钝头体的飞行器在超声速特别是高超声速条件下，其前缘会形成头部弓形激波，进而带来较大的波阻，严重影响飞行器的气动性能。相关研究表明，在高超声速条件下，钝前缘安装激波针可以将激波推离物面，从而减小头部表面压力，是减小超声速钝体阻力的有效方法，但在超声速，特别是一些巡航速度不高（马赫数Ma=1.5左右）的导弹中，为满足射程等相关要求，对激波针减阻的使用价值还有待进行验证。为了研究激波针在Ma=1.5条件下对轴对称钝锥外形气动特性的影响，通过数值模拟方法对比了不同形状激波针在Ma=1.5条件下的减阻效果，分析了减阻机理及外形参数影响；通过基于Kriging和遗传算法相结合的优化方法对主要外形参数进行了优化设计，给出了减阻效果较好的激波针外形参数选取范围，对工程应用具有一定的借鉴意义。

兵器科学与技术；激波针；阻力特性；激波；Kriging模型；优化

0 引言

头部装有雷达或红外制导系统的飞行器，需要采用较钝的头部以满足导引头空间布置的需要，另外，高超声速飞行器采用钝头体主要基于防热的需要。然而，对于钝头体飞行器来说，在超声速特别是高超声速条件下形成的头部弓形激波，使得头部表面压力较高，进而带来较大的阻力，严重影响飞行器的气动性能。在钝前缘安装激波针可以把激波推离物面并在头部形成低压回流区，从而减小头部表面的压力，对超声速飞行器巡航状态下的波阻减小量可高达50%，是减小超声速钝体阻力最简单有效的方法［1-3］。

大量关于激波针气动特性的计算和实验研究主要在高超声速条件下开展的，而在马赫数较低的超声速范围，由于钝头体飞行器外形的激波强度较高超声速时弱，安装激波针的减阻效果可能有限，因而没有引起研究者的重视。针对某导弹射程需要，为了探索超声速（马赫数Ma=1.5）条件下在轴对称钝锥外形弹体头部安装激波针的可行性，以及评估激波针对全弹气动特性的影响，通过数值模拟方法对不同激波针外形进行了对比研究，分析了激波针的减阻机理和主要影响参数，最后基于Kringing和遗传算法相结合的优化方法对主要的外形参数进行了优化设计，给出了减阻效果较好的激波针外形参数选取范围。

1 计算外形与优化方法

1.1计算外形

基于文献［4］所述的带激波针的半球形钝头体外形，全弹具有半球体头部，旋成体弹身以及收缩尾段，激波针为半球体头部和旋成体弹身（见图1）及其在Ma=1.89时的气动特性试验结果，对拟提出的数值模拟方法和网格划分进行了验证。

图1　带激波针的半球形钝头体外形示意图Fig.1 Selected model of hemispherical blunt-noised body with spike

在保持激波针总长和激波针旋成体弹身直径不变的情况下，通过改变激波针的头部形状，研究了4种不同形状激波针外形对轴对称钝锥外形气动特性的影响，如图2所示。图2中:激波针1为半球盘结构，直径为d；激波针2为平面形状，头部直径为d；激波针3为椭球锥外形，最大宽度直径为d；激波针4为圆锥形外形，锥角为20°.

1.2优化方法

与其他近似模拟技术相比，Kriging是一种更具有“统计性”的近似技术。同时，kriging模型的有效性并不依赖于随机误差的存在，即己知信息中是否包含噪声信息不会影响kriging模拟的有效性程度［5］。

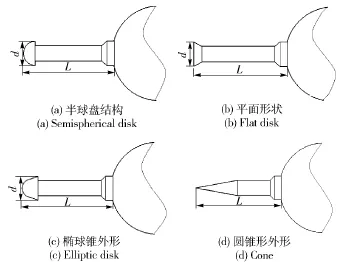
图2　不同激波针外形示意图Fig.2 Four models of spike

一般来说，Kriging模型包含两部分:多项式和随机分布，具体模型为

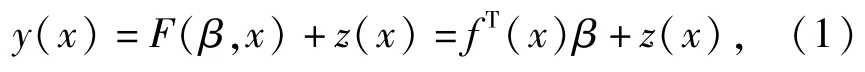
式中:β为回归系数；f（x）为变量x的多项式；z（x）服从正态分布N（0，σ2），其协方差矩阵为Cov［z（xi），z（xj）］=σ2［R（xi，xj）］，R（xi，xj）为ns个样本点中任何两个样本点xi和xj的空间相关方程，它对模拟的精确程度起决定性作用。其中计算效果最好，被广泛采用的相关方程是高斯相关方程

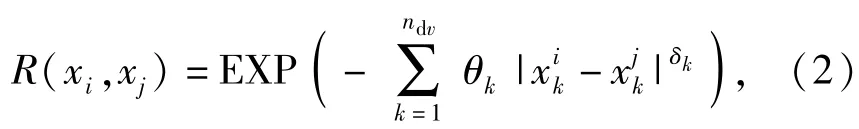
式中:ndv是已知设计变量的数量和是样本点xi和xj的第k个分量；待定参数θk为相关性参数；δk为光滑程度参数，0≤δk≤2，本文δk=1.5.

根据模型要求预测模型的方差最小，可以得出待测点的响应估计值为

式中:r（x）为点x与ns个样本点之间的相关向量；β*为参数β的极大似然估计。所以对于每一个新的样本，只需要求出f和r，就可以估计新样本的响应值。z（x）服从正态分布，那么y（x）也服从正态分布。它的对数似然函数为

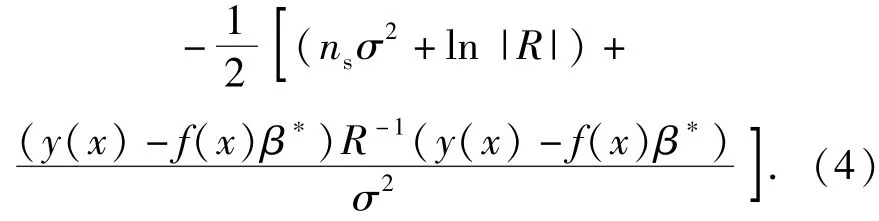
在给定参数θk的情况下，（4）式对β*和σ2求导，可以得到它们的极大似然估计为

将β*和σ2代入（3）式可以得到如下的最大化问题:

综上所述，最优Kriging模型的构造问题被转换为非线性的无约束优化问题。任意一个θk值都能生成一个插值模型，最终Kriging模型是通过利用优化方法找到最优的θk值使得似然函数最大，从而使得构造的模型精度最高。

2 计算结果与分析

2.1数值模拟方法有效性检验

控制方程采用雷诺平均的Navier-Stokes方程，采用有限体积法进行空间离散，空间无黏通量采用ROE格式进行离散，黏性通量采用2阶中心差分格式离散，时间项采用隐式LU-SGS方法求解。为加快收敛速度，采用局部时间步长和多重网格技术。湍流模型是两方程k-ωSST模型。

图3为绕激波针钝头体的流场结构示意图。绕半球盘和平面盘激波针钝头体外形主要由弓形激波、大分离区、再附激波和分离激波为主体结构的基本流动模型［6-8］。

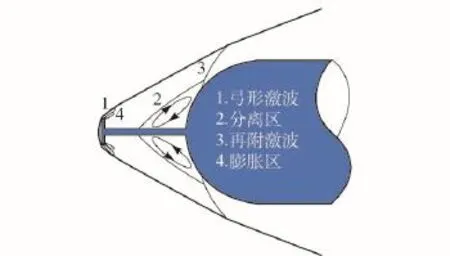
图3　绕激波针钝头体的流场结构示意图Fig.3 Flow field structure around blunt-nosed body with spike

图4给出了不同攻角δ下的升力系数CL和阻力系数CD计算结果和试验值的对比。从图4中可以看出，升力系数计算结果和实验值吻合得较好，光弹身和带半球体激波针外形阻力系数计算结果与试验值相比都有约10%左右的增量误差，这主要与网格量和湍流模式有关，但是激波针对阻力系数影响量的计算结果和试验值吻合得较好，可认为本文采用的数值计算方法研究激波针气动特性的影响是有效的。

图4　Ma=1.89时升力和阻力系数计算结果与试验结果的对比Fig.4 Comparison of CFD calculated and experimental results for Ma=1.89

2.2不同激波针减阻效果对比

上述5种激波针外形的减阻效果在Ma=1.5，δ=0°下的对比结果如图5所示。

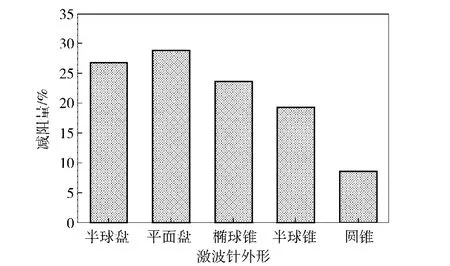
图5　Ma=1.5和δ=0°时不同形状激波针减阻效果对比Fig.5 Drag reduction for different spike models for Ma=1.5 and δ=0°

从图5可以看出在该条件下，与光弹身相比，5种带激波针外形都有一定的减阻效果，减阻量在8.6%～28.9%之间；激波针外形的不同对激波针的减阻效果影响较大，减阻效果最好的激波针外形为平面盘形，与光弹身相比减阻量约为28.9%，半球盘减阻效果次之约为26.8%，随后是椭球和半球体激波针，减阻量分别为23.7%和19.3%，圆锥形激波针减阻效果最差，减阻量仅为8.6%.

图6给出了δ=0°时光弹身、带半球盘和平面盘激波针外形对称剖面头部前缘压力系数CP的对比，θ为周向角。从图6中可以看出，光弹身外形靠近头部前缘位置压力系数明显高于带激波针外形，平面盘激波针外形压力系数在弹体头部前缘略小于半球盘外形，这也解释了图5所示的平面盘外形减阻效果优于半球盘的的原因。从图6中还可以看出，在弹体头部中、后缘（θ＞30°）两种激波针外形的对弹体表面的压力系数影响趋于一致，并且弹体表面的压力系数都要高于光弹身外形。这也说明激波针外形主要通过降低弹体头部前缘表面的压力系数来达到减阻的效果，不同激波针外形对弹体后缘压力系数的影响趋于一致。

图6　Ma=1.5和δ=0°时弹体头部压力系数对比Fig.6 Pressure coefficients on forebody nose for Ma=1.5 and δ=0°

图7给出了δ=0°时半球盘和平面盘外形对称剖面马赫数云图对比。从图7中可以看出，两种激波针外形的波系是相似的，不同的是平面盘前缘激波和弹体前缘激波的交点距弹体肩部的距离（约为2.25D，D为弹身直径）要大于半球盘外形（约为1.45D），还可以看出两种激波针外形在弹体头部前缘都形成了较大的回流区，平面盘外形回流区的涡心位置和壁面再附点位置的纵向距离都略大于半球盘外形。

图8给出了δ=0°时半球盘和平面盘激波针外形和光弹身外形阻力系数随马赫数变化的对比。从图8中可以看出，两种激波针外形在超声速范围都具有明显的减阻效果，并且减阻效果随马赫数的增大而增加，激波针在亚声速、跨声速会带来一定的附加阻力，造成带激波针外形较光弹身外形阻力的增加，另外，由于平面盘为钝前缘，在亚声速、跨声速的附加阻力要大于半球盘外形。

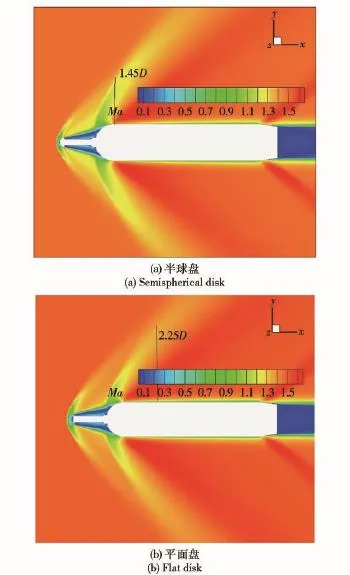
图7　Ma=1.5和δ=0°时对称剖面马赫数云图对比Fig.7 Mach number counters for Ma=1.5 and δ=0°图8　δ=0°

图8　δ=0°时3种外形阻力系数随马赫数的变化Fig.8 Drag coefficient versus Mach number for δ=0°

因此，半球盘形激波针外形在兼顾亚声速、跨声速、超声速减阻效果方面是5种激波针中最好的。另外，当Ma=1.5时，由图9升力系数随攻角变化曲线可以看出，安装激波针对弹体布局的升力系数影响较小。

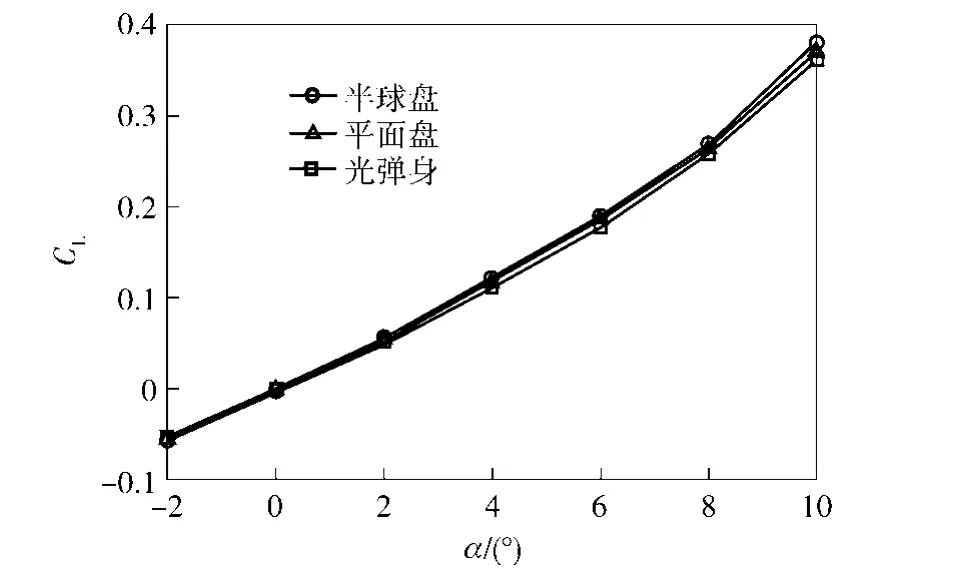
图9　Ma=1.5时升力系数随攻角变化Fig.9 Lift coefficient versus angle of attack for Ma=1.5

3 激波针外形参数优化

对原始外形进行参数化建模，通过优化设计变量L、R、l、r的值达到减阻目的，对应的外形参数如图10所示。其中:L为激波针总长度；r为激波针头部最大截面半径；l为激波针头部长度；R为激波针头部钝化半径。

图10　优化外形参数示意图Fig.10 Optimized parameters of base model

图11　相应曲面Fig.11 Response surface

图12　优化前后外形示意图Fig.12 Comparison of original and optimized models

为了简化激波针头部外形描述，定义两个系数代替参数l和r:

激波针头部钝化半径比:k_rR=r/R；

激波针头部长细比:k_lR=l/R.

优化问题可以归纳为:

设计变量:L∈［30mm，90mm］，R∈［4mm，10mm］，k_rR∈［0.2，1.0］，k_lR∈［0.5，3.0］。

目标函数:minCD.

采用全局优化方法遗传算法，优化迭代639步。设计变量L、R与目标函数CD的相应值如图11所示。

从图11中可以看出，阻力最小值在L、R的最大边界位置附近，优化空间内最优值为:L=90mm（边界值），R=10mm（边界值），k_rR=0.6（即r= 6mm），k_lR=1.75（即l=17.5mm），此时与原始外形相比阻力降低量约为10.2%，与不带激波针外形相比阻力降低33.7%.优化前后外形参数对比如图12所示，可以看出优化后激波针长度和激波针头部最大截面半径增大较多，优化后激波针长度与弹径的比L/D=1.268，与相关文献［9］中所述在超声速时激波针长度L/D的取值在1.3附近时减阻效果最好的结论一致。然而激波针长度的增加会一定程度上降低结构强度，为进一步认识阻力系数与激波针长度的关系，固定R=10mm，k_rR=0.6（即r= 6mm），k_lR=1.75，仅改变激波针的长度，设计变量L与目标函数CD的关系如图13所示，图13中初始外形L=66.1mm对应CD=0.6017，由此可见，随L值变大，零阻单调变小，在选取的优化空间内L= 90mm时模型零阻最小，最小值0.5694.但考虑到增加伸长杆长度将减小其结构强度，同时观察图13中3号点至1号点零阻变化很小，实际可选取3号点。如需进一步提高伸长杆强度，也可选择5号点。

图13　阻力系数随激波针长度的变化Fig.13 Dragcoefficientversusspikelength

4 结论

1）激波针的主要作用是把激波推离物面并在头部形成低压回流区，从而减小头部表面的压力，达到降低钝头体外形的阻力。

2）在Ma=1.5时，激波针外形对钝头体具有一定的减阻效果，并且激波针头部形状对减阻效果影响较大，在前缘能够形成脱体弓形激波的激波针外形的减阻效果要优于形成锥形激波的激波针外形。

3）激波针长度取弹身直径的1.3倍左右减阻效果最好，但是综合考虑激波针的结构强度和可能因尺寸过大引起的激波振荡，在激波针尺寸的选择中不能只关注减阻效果，需要综合考虑。

（References）

［1］ Asif M，Zahir S，Kamran N，et al.Computational investigations aerodynamic forces at supersonic/hypersonic flow past a blunt body with various forward facing spikes，AIAA-2004-5189［R］.Reston，VA，US:AIAA，2004.

［2］ Srulijes J，Gnemmi P，Runne K，et al.High-pressure shock tunnel experiment and CFD calculations on spike-tipped blunt bodies，AIAA-2002-2918［R］.Reston，VA，US:AIAA，2002.

［3］ 姜维.高超声速飞行器减阻杆气动特性研究［D］.长沙:国防科学技术大学，2012:42-45. JIANG Wei.Investigations on aerodynamics of a spike-tipped hypersonic vehicle［D］.Changsha:National University of Defense Technology，2012:42-45.（in Chinese）

［4］ Milicev S S，Pavlovic D.Influence of spike shape at supersonic flow past blunt-nosed bodies:experimental study［J］.AIAA Journal，2002，40（5）:1018-1020.

［5］ 王红，王希诚，李克秋.混合Kriging代理模型的高维参数估计优化算法［J］.大连理工大学学报，2015，55（2）:215-219. WANG Hong，WANG Xi-cheng，LI Ke-qiu.Hybrid Kriging surrogate model optimization algorithm for high-dimension parameter estimation［J］.Journal of Dalian University of Technology，2015，55（2）:215-219.（in Chinese）

［6］ 侯文新，吴颂平.带激波针的高超声速飞行器多目标优化设计［J］.战术导弹技术，2015（2）:23-27. HOU Wen-xin，WU Song-ping.Multi-objective optimization design of hypersonic spiked bodies［J］.Tactical Missile Technology，2015（2）:23-27.（in Chinese）

［7］ 张江，彭程，蔡琛芳，等.基于响应面法的带喷流激波针参数优化研究［J］.空气动力学学报，2015，33（2）:204-210. ZHANG Jiang，PENG Cheng，CAI Chen-fang，et al.Optimization research on combination of spike and forward-facing jet using response surface methodology［J］.Acta Aerodynamica Sinica，2015，33（2）:204-210.（in Chinese）

［8］ Menezes V，Saravanan S，Jagadeesh G，et al.Experimental investigations of hypersonic flow over highly blunted cones with aerospikes［J］.AIAA Journal，2003，41（10）:1955-1966.

［9］ Gnemmi P，Srulijes J，Roussel K，et al.Flowfield around spiketipped bodies for high attack angles at Mach 4.5［J］.Journal of Spacecraft and Rockets，2003，40（5）:622-631.

Drag Reduction Characteristics and Design Optimization of Spikes

LI Yong-hong，GAO Chuan，TANG Xin-wu
（High Speed Aerodynamic Institute，China Aerodynamics Research and Development Center，Mianyang 621000，Sichuan，China）

Taking into account the configuration or aerodynamic heating，most hypersonic flight vehicles have to use the blunt-nosed body.A strong bow shock forms ahead of the blunt nose to introduce a rather high shock drag in supersonic flow，especially in hypersonic flow，that affects the aerodynamic performance of the vehicles seriously.A spike mounted on a blunt-noised body pushes the strong bow shock away from the body surface，which forms recirculation flow with low pressure ahead of the body surface，and then decreases the drag.The drag reduction effects of spikes in high supersonic and hypersonic flows are validated through experimental and numerical methods.In order to analyze the influence of spike on aerodynamic characteristics of blunt-nosed body in supersonic（Ma=1.5）flow，the numerical studies are carried out.The design optimization of spike shape is carried out based on Kriging model and genetic algorithm.

ordnance science and technology；spike；drag characteristic；shock wave；Kriging model；optimization

V211.3

A

1000-1093（2016）08-1415-06

10.3969/j.issn.1000-1093.2016.08.011

2016-01-06

李永红（1986—），男，工程师。E-mail:hello_niu1@163.com