广义Nekrasovrasov矩阵的一组充分条件

郭爱丽，邓慧琳

（贵州工程应用技术学院理学院，贵州 毕节 551700）

广义Nekrasovrasov矩阵的一组充分条件

郭爱丽，邓慧琳

（贵州工程应用技术学院理学院，贵州 毕节 551700）

利用定义和不等式的放缩给出广义Nekrasov矩阵的一组充分条件，改进和推广了已有相关结果，并用数值实例说明了所得结果的有效性。

广义Nekrasov矩阵；Nekrasov矩阵；对角矩阵;广义严格对角占优矩阵

1　引言

广义Nekrasov矩阵在计算数学、数学物理及控制系统等领域有着重要的应用，其判定问题是近年来研究的热点问题之一。本文在判定广义Nekrasov矩阵一系列经典研究结果的基础上，利用定义结合不等式的放缩给出广义Nekrasov矩阵的一组判别条件，改进和推广了文献[1]的结果，并用相应的数值实例说明了所得结果的有效性。

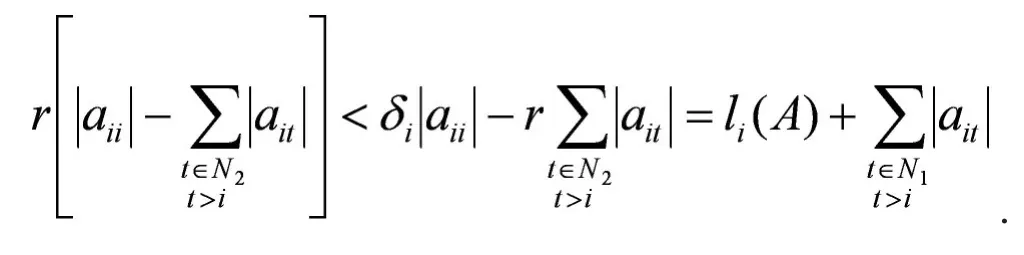
即

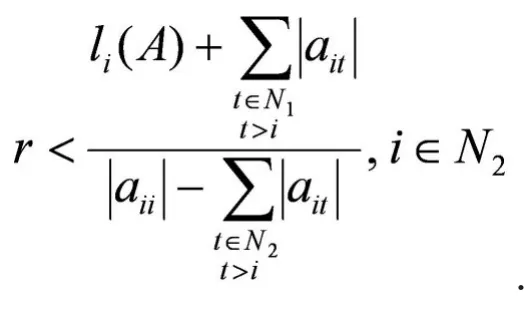
证毕。

由引理5知广义Nekrasov矩阵是一类特殊的广义严格对角占优矩阵，因此，本文相应地也得到了判定广义严格对角占优矩阵的一类方法。

2　主要结果

本节利用定义，结合不等式的放缩技巧给出广义Nekrasov矩阵的一组判别条件。

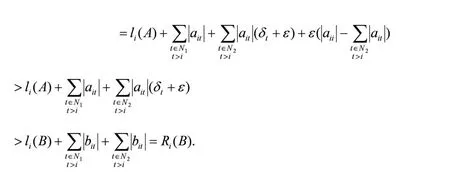
证毕。

3　数值实例

例设矩阵

[1]郭爱丽,刘建州.广义Nekrasov矩阵的充分条件[J].数学的实践与认识,2013(3):189-195.

[2]郭爱丽,周立新.广义Nekrasov矩阵的一类递进判别法[J].重庆工商大学学报,2014(8):59-63.

[3]郭爱丽.广义Nekrasov矩阵的实用性新判定[J].毕节学院学报,2012(8):59-63.

[4]郭爱丽,刘建州.广义Nekrasov矩阵的判定[J].工程数学学报,2009(4):697-702.

[5]郭爱丽.广义Nekrasov矩阵的迭代判别法[J].毕节学院学报,2009(4):66-69.

[6]Li W.On Nekrasov matrices[J].Linear Algebra Appl,1998(87):87-96.

[7]WANG Q,SONG Y ZH,LI W Q.Estimates of upper bounds of the spectral radius for some iteration matrices[J].Jouranl of Nanjing university mathematical biquarteraly,2005(22):96-106.

[8]Szulc T.Some remarks on a theorem of Gudkov[J].Lin Alg Appl,1995（225）:236-242.

[9]PANG M X,ZHU X L.Generalized Nekrasov matrices and applications[J].Journal of Computational Mathematics,2003(21):183-188.

A Set of Criteria for Generalized Nekrasov Matrices

GUO Ai-li，DENG Hui-lin
（The Faculty of science,Guizhou University of Engineering Science,Bijie,Guizhou551700,China）

A set of criteria for generalized Nekrasov matrices is given by the definition and the tech⁃niques of inequalities,which improves the existing and related results.Furthermore,the effectiveness of the proposed result is confirmed by a numerical example.

Generalized Nekrasov Matrices;Nekrasov Matrices;Positive Diagonal Matrices;General⁃ized Strictly Diagonally Dominant Matrices

O151.21

A

2096-0239（2016）02-0139-05

（责编：彭麟淋责校：明茂修）

2016-03-21

贵州省科技厅联合基金项目“特殊矩阵类的性质及应用研究”，项目编号：2015GZ62783。

郭爱丽（1979－），女，山东菏泽人，贵州工程应用技术学院理学院副教授，硕士。研究方向：矩阵理论及其应用。