超微晶合金旋转磁特性测量用励磁装置的设计与优化

陈 龙 汪友华 赵浛宇 戈文祺 王 苗



超微晶合金旋转磁特性测量用励磁装置的设计与优化

陈 龙 汪友华 赵浛宇 戈文祺 王 苗

（河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130）

旋转磁心损耗广泛存在于高频变压器T形连接点处与高速电机的定子上。为了对二者进行更好的分析，需要将高频下的旋转磁心损耗进行精确测量。本文就四种不同的励磁结构进行有限元分析，阐述了励磁结构对准确度的影响。在此基础上，根据超微晶物理特性提出一种立体式二维高频励磁装置，对励磁绕组进行计算，并优化设计了磁轭结构，将测试频率提高到10kHz。

超微晶合金 二维旋转磁特性 高频励磁装置 优化设计

0 引言

高速电机与高频电工设备由于其较高的功率密度，而具有广泛的应用前景[1-4]。超微晶合金与非晶合金等新兴材料被广泛应用于各种高频领域[5]。但是，目前仅限于一维超微晶磁特性的测量[6]。日本学者测试了二维非晶合金，但频率最高只达到750Hz[7]。为了在电机设计过程中更有效地分析材料在高频下的损耗，有必要对超微晶合金的高频旋转磁特性进行精确测量。

当频率达到1kHz以上时，二维磁化问题变得十分复杂，相比一维，其对励磁电源提出了更高要求。在保证样片磁化均匀的前提下，选择合适的励磁结构显得尤为重要。

目前世界上对二维旋转磁化问题的研究已有三十多年[8]，早期的旋转磁特性主要是通过测量样片在旋转过程中受到的转矩，计算其旋转一周的平均损耗[6]。但这种方法校准十分困难，很难分离出在旋转过程中因摩擦力等因素带来的误差。自1965年起，有学者开始研究用温度传感法测量旋转磁心损耗，其表达式为

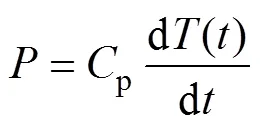
式中，p、()分别为被测样片的比热和温度。该方法在磁通密度较高时有较好的准确度和灵敏度，但磁通密度较低时灵敏性较差，并且对样片绝热十分困难，因此，限制了该方法的广泛应用。磁场计算测量法由于实施简单、准确度高、可重复性好，得到了国际上的广泛认可。在磁场计算测量法中，通过样片磁化后测得的磁场强度和磁通密度可得到磁心损耗，由坡印亭定理经过一系列推导可得旋转磁心比损耗t为

（2）

为了在样片中模拟变压器T形连接点与电机齿部所产生的旋转磁场，德国、意大利、奥地利和日本学者分别建立了不同的励磁装置[9-14]。这些装置大体上可按样片形状分为三类：基于方形样片的十字形单片测量仪（Square Rotational Single Sheet Tester, SRSST）、基于六边形样片的单片测量仪（Hexagonal Rotational Single Sheet Tester, HRSST）和基于圆形样片的类感应电机式单片测量仪（Round Rotational Single Sheet Tester, RRSST）。但这些装置都只适合低频情况下的励磁（几百Hz）。为了测试更高频率，意大利国家计量学院研制了基于三相励磁的二维高频励磁装置（3 Phase-RRSST, 3P-RRSST）[15]，其是在原类电机励磁结构的基础上进行了改进，采用集中绕组，减小了每相绕组的磁通，从而将测试频率提高到5kHz。然而国际上还没有形成统一的二维磁特性测量标准，其中一部分原因是二维磁特性测量的可重复性较差，各种测量装置测量结果有一定偏差[16]。

本文分别建立上述四种主要励磁装置的有限元模型，以15°为步长分析了样片的磁化性能。首先，对比了不同装置磁化对样片均匀性的影响；其次，分析了不同结构的励磁性能；最后，根据分析结论，考虑超微晶合金本身的物理特性[17]，提出一种适合超微晶二维高频磁特性测量的立体式励磁装置。

1 励磁结构对样片磁化均匀性的影响

样片形状与其对应的励磁结构对样片磁化的均匀性有重要影响。四种不同的励磁结构如图1所示。SRSST结构最早由W. Brix提出[18]，之后有很多改进版本[19-24]。其主要原理是在空间相对正交的两个磁极上缠绕绕组，通有相位正交的两相电流，在样片中产生旋转磁场。HRSST由H. Pfützner于1996年提出[25]，由于该结构采用多对磁极的三相励磁系统，使矢量的轨迹更接近圆形。RRSST将传统感应电机的转子替换为圆形样片，如图1c所示，在定子中缠绕正交分布的两相分布式绕组，在较低磁通密度下无反馈控制也可以达到圆形旋转磁场。3P- RRSST[26]结构如图1d所示，此结构由于是三相励磁，在波形上更容易实现圆形控制。

（a）SRSST   （b）HRSST

（c）RRSST   （d）3P-RRSS

图1 四种不同的励磁结构

Fig.1 Four different structure of magnetizer

测量过程中，样片中央位置分别在方向和方向上垂直放置两组H线圈与B线圈。从而用一定区域内磁场的均值来模拟中心点处磁场的大小和方向。磁场矢量计算式为

（4）

为了得到更精确的结果，样片磁化的均匀性对测量结果起着重要的影响。气隙作为样片磁化中非常关键的参数，对磁化的均匀度影响很大。这主要是由于不同气隙条件下样片中退磁场分布不均，而退磁场随气隙的减小而减小。考虑到实际加工的准确度，这个值并不能无限减小。而文献[27]未提及气隙的影响，为了说明励磁结构对样片均匀性的单一影响，本文所分析的四种结构使用统一的参数：气隙大小=0.5mm，样片内切圆直径。

计算过程中，不考虑样片材料的各向异性，认为样片在不同方向上具有相同的磁化曲线。为了得到更精确的结果，样片部分网格剖分采用极端细化网格，样片被磁化到1T左右。当磁化角度为45°时，四种结构中样片的磁力线分布与磁通密度分布分别如图2和图3所示。

（a）SRSST

（b）HRSST

（c）RRSST

（d）3P-RRSST

图2 不同励磁装置的磁力线分布

Fig.2 Flux lines distribution of differnet magnetizers

（a）SRSST

（b）HRSST

（c）RRSST

（d）3P-RRSST

图3 不同励磁装置的磁通密度分布

Fig.3 Magnetic flux density distribution of different magnetizers

由图2和图3可知，方形样片和六边形样片所对应的励磁结构在顶角处磁通密度较高，但样片整体磁通密度分布比较均匀。而圆形样片对应的励磁结构，由于存在齿槽效应，样片边缘的磁通密度变化剧烈，缩小了样片的可测量范围，对于两相感应电机式励磁装置，存在明显的弱磁区，磁力线在对应磁化角度45°与135°的区域向两边分散，导致这部分的磁通密度较低。而对三相励磁结构各相磁通进行了补偿，没有出现明显的弱磁区，但是齿槽磁阻周期性变化剧烈，导致了磁通密度随圆周振荡剧烈。在方形样片与六边形样片的励磁装置中，由于微小气隙的存在（=0.5mm），减小了磁极间的相互吸引，使磁力线大部分从样片中经过，减小了漏磁，因此导致样片的磁通密度分布相对均匀。

为了进一步定量分析样片的均匀性，将样片上各点磁通密度标准差作为定量分析样片均匀性的标准，其计算式为

式中，x为样片区域内每个点的磁通密度大小；为整个样片磁通密度的均值。

图4和图5分别给出了半个周期内样片磁通密度分布的标准差与均值随着角度变化的分布。如图4所示，在相同气隙条件下，四种结构中方形样片所对应的SRSST具有最小的标准差，磁通密度分布在整个样片的变化最小，六边形样片次之。这与图3磁通密度三维云图的结果是吻合的。圆形样片所对应的RRSST与3P-RRSST的标准差较高，反映出弱磁区与齿槽效应对样片均匀性的影响。方形样片与六边形样片在不同磁化角度上的标准差出现不同程度的振荡，而圆形样片在不同角度上变化很小，说明圆形样片在不同磁化角度上的磁化状态是一致的。图5进一步验证了上述观点。圆形样片在一个磁化周期内样片内的磁通密度基本保持不变，而方形样片和六边形样片由于磁路不对称，在不同角度上表现出不同的磁化能力。对于方形样片SRSST在45°、135°等方向上，在气隙中磁力线长度大于0°、90°与180°的情况，相对磁阻较大，从而在相同的磁动势下这些角度上的磁通密度相对较低。类似的结论也可以从六边形样片的励磁结构中得到。而圆形样片由于磁路对称，在不同磁化角度上磁阻处处相等，磁通密度大小保持恒定，可以实现标准圆形磁化。

图4 磁通密度标准差随磁化角度的分布

图5 磁通密度均值随磁化角度的分布

由上面分析可知，在不考虑材料各向异性的情况下，从样片均匀度的角度考虑，方形样片具有更低的磁通密度变化；从实现圆形控制角度考虑，圆形样片更容易达到开环的圆形旋转磁场，而降低了对控制程序的要求。但是超微晶合金材料不是完全的各向同性，所以无论哪种结构都需要反馈的调节。对于方形样片和六边形样片，在实际测量过程中需要更强的反馈算法才能保证圆形旋转磁场的实现。通过考察整体的标准差和图3的磁通密度云图，可为传感器的设计提供理论指导，从而进一步提高高频磁场测量的传感器灵敏度。

2 超微晶磁心励磁结构设计

由励磁结构对样片磁化均匀性的分析可知，当样片被磁化到1T时，基于方形样片的SRSST在一个周期内的各个角度上均具有最好的均匀性。超微晶磁心的饱和磁通密度在1.23T左右，完全满足测量需求。考虑到超微晶带材宽度一般为50mm且易碎，圆形样片的加工成本远超过方形样片。在均匀度满足要求的前提下，综合考虑，本文设计了基于方形样片的超微晶高频旋转测量装置。由于超微晶合金通常应用在高频领域，而传统的SRSST只能工作在几百Hz的频率下，所以需要在传统的励磁结构上进行改进。本文提出的超微晶高频旋转励磁装置如图6所示，可将测试频率提高到10kHz。

（a）模型     （b）实物

2.1 励磁结构的磁路设计

当频率达到1kHz以上时，磁心的发热问题及磁场的建立都变得十分困难。若用传统的硅钢叠制成磁心，在10kHz时磁心发热十分严重，容易破坏绕组绝缘，引起安全问题。超微晶带材拥有超高的磁导率及在高频下接近硅钢1/10的损耗[28]，非常适合在频率1～20kHz的频段内工作。所以本文以超微晶材料作为制作磁心的带材。对于传统的平面式SRSST[29]，采用四个磁极与四个L形磁轭构成闭合磁路，在磁极与L形磁轭连接处，磁通垂直传入带材表面，引起较大涡流损耗，并且绝缘介质增大了磁动势降落，导致需要更大的电流才能将样片磁化到饱和，这样提高了对电源的要求。本文提出的双C形立体式励磁结构有效地避免了这一问题，并且两条相互垂直的磁路相互独立，可以分开计算。若忽略漏磁场，由安培环路定律得

式中，y、s分别为磁心截面积与样片截面积；ys分别为磁心磁通密度与样片磁通密度。实际情况下，由于漏磁通的存在，样片磁通并不完全等于磁心磁通。由于被测样片极薄，空气中的漏磁通a可由不放样片时测得，从而计算得到考虑漏磁场下的修正系数a，则式（7）可修正为

（8）

由式（6）可知，为了避免磁心过热，应降低磁心磁通密度y，因而磁心应保证一定的厚度。

2.2 几何结构的优化

本文为了减小高频的电容效应，将绕组分别缠绕在了两只磁心的磁轭上，而这样会增加磁极杂散磁场的分布，这部分磁场会缩小样片均匀区域的大小，影响样片的均匀性。磁屏蔽层对样片均匀性的影响如图7a和图7b所示。由图7可见，在没有屏蔽层的情况下，通过三维有限元计算可发现，磁极中的一部分磁通在空气中与另一边磁极闭合，导致在样片边缘处的磁场要小于中心部位。而增加了屏蔽层后，外部磁场在屏蔽层处闭合，屏蔽层内部没有杂散磁场，样片的均匀区域几乎扩大到整个样片。此外，在高频测量时，如何有效去除与测量频率接近的空间谐波是一大难题。由于屏蔽层的存在，屏蔽层内部空间可避免外界磁场的干扰，这对高频测量十分重要，可有效分离出有效信号，提高测量准确度。

（a）磁力线分布（未加屏蔽层） （b）磁通密度分布（未加屏蔽层）

（c）磁力线分布（加屏蔽层） （d）磁通密度分布（加屏蔽层）

图7 磁屏蔽层对样片均匀性的影响

Fig.7 Influence of the magnetic shielding on sample uniformity

在考虑屏蔽层后，屏蔽层与样片的距离、磁极间各部分的尺寸也显得尤为重要。文献[30,31]分析了当磁极形状为楔形时，具有较好的聚磁效果；当楔角为54.5°时，中心获得最大磁场。但实际气隙存在样片时，磁路接近闭合磁路的情况，样片的存在将影响周围空间磁场的分布，最优的楔角还需要进一步修正。由于在考虑样片时，不能得到精确的解析表达式，本文以当样片被磁化到1T时所需的功率为优化目标，以自适应模拟退火法[32]作为优化算法，对这一问题进行了优化。磁极尺寸的设计参数如图8所示。

图8 磁极尺寸的设计参数

图8中，1为磁心磁轭厚度，2为磁极高度，3为磁极长度，4为屏蔽层到样片的距离。气隙大小没有作为优化设计的变量，气隙越小，所需磁动势越小，样片均匀性的退磁磁场越小。由于机械加工准确度的原因，本文设计的超微晶磁心样片与磁极的距离设定为0.3mm。由于=[1234]这一组变量，并不是相互独立的，所以不能通过参数化扫描的方式来确定最终的尺寸，需要进行全局优化。本文通过Comsol与Matlab联合仿真，在Matlab中编写优化算法，实现了对参数的优化。优化问题可总结为

（11）

式中，coil()、p()分别为当样片磁通密度为1T时绕组的电压和电流，可通过对磁心有限元模型进行频域分析得到；为设计变量，=[1,2,3,4]，下限min为几何尺寸的约束，min[2, 0.2, 0.2, 0.2]，上限max[25, 25, 25, 5]。考虑楔角的极限情况，为保证磁极的楔形，有

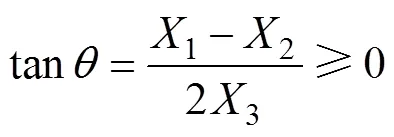
（1）初始化。设定可行域，最大温度max，下降速率，步长，初始min及每一代的个体数rp。

（2）在T温度下，按一定规律随机产生一个步长，生成rp个个体，通过有限元计算，计算每个个体的目标函数值S。

（3）每个S与min作比较，若S≤min则接受，并更新min；若S＞min则按式（13）进行判断。

式中，为[0,1]上的伪随机数；为玻耳兹曼概率。在整个过程中，统计T下S＞min的次数1与被接受的次数2。

（4）降低温度T并回到步骤（2）迭代。若2/1偏大，则优化过程中限制了下山性，加大下降速率；若2/1偏小，则限制了上山性，此时T下降速率应比原来小一些。

这样，经过反复迭代，得到磁极初始与优化后的尺寸见表1。由表1可看出，最终的优化尺寸对电源功率的需求降低了36%，提高了高频励磁装置的励磁能力。

表1 磁极初始与优化后的尺寸

Tab.1 Initial and optimal size of the magnetic pole

2.3 励磁绕组的设计

当频率升高时，导体之间的电容效应、趋肤效应和邻近效应不能忽略。为减小高频时两相绕组的电容效应，将单层绕组缠绕在磁心的轭部上，由于磁心厚度远大于样片厚度，即使样片饱和，磁心磁通密度仍然较低，具有较高的磁导率，因此漏磁较小，可忽略不计。为了减小高频时绕组的趋肤效应与邻近效应带来的损耗，用litz线制作了单层绕组，litz线单根导体半径为

式中，Cu为铜的电阻率；0为真空磁导率；max为最高实验频率。由于litz线采用ETFE绝缘，极限温升可达155℃，最大电流密度为5A/mm2，因此，绕组最大电流为

（15）

式中，Cu为单根导线截面积；max为导体能承受的最大电流密度。最终匝数为

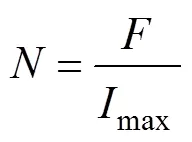
式中，为磁动势。通过三维有限元计算可得到，当样片被磁化到1T时，litz线电流为8.9A，对应绕组的匝数为12匝、绕组长度为37.5mm。最终绕组的电感可由计算磁场能量得到，直流电阻由LCR分析仪测得为0.061W。为减小高频的损耗，本文采用的litz绕组线径为0.01mm，分5股，每股60匝，共300根漆包线。在10kHz时，交流电阻为直流电阻的5倍，相较电抗的变化，整体阻抗主要由电抗决定。为了减小电抗以适应更高频率的测试，须减小最终设计的励磁电感。本文设计的litz绕组实际上是增大了单位通流能力，从而在保证安匝数不变的情况下，减小了匝数，进而减小了励磁电感。励磁绕组电压为

（17）

式中，ac为绕组等效交流电阻；为绕组等效电感；为绕组电流。

当频率为10kHz时，绕组上的励磁电压为65.52V，对应电感为0.116mH，由此得到视在功率=589V·A。为了将样片磁化到更接近饱和，在10kHz条件下，两相绕组分别加载10A电流，可由实验室购买的功放AE 7548安全提供。

3 实验装置的可行性

高频旋转励磁装置的励磁实验系统如图9所示，主要包括以下几部分：美国NI公司提供的PXI测试平台，通过高性能的多功能DAQ卡实现信号的产生并采集；两台高性能的线性功放，可以实现DC～50kHz的功率放大，为超微晶高频励磁装置提供励磁电流；超微晶二维高频励磁装置及复合式B&H传感器。当磁通密度较小时，传感器产生的信号较小，且周围空间中存在一些干扰磁场。对传感器信号的前置处理如图10所示，本课题组通过SR560得到了较好的结果。图11给出了当p=1.0T、= 10kHz时两相绕组上的电压和电流波形，可看出电流波形基本符合计算结果，而电压略高于计算值，这主要是因为litz线在高频时交流电阻的上升，但并不影响整体实验。

（a）实验框图

（b）实物图

图9 高频旋转励磁装置的励磁实验系统

Fig.9 Exciting experiment system of the high frequency rotational magnetizer

（a）处理前

（b）处理后

图10 对传感器信号的前置处理

Fig.10 Preprocessing of the sensor signal

图11 两相绕组上的电压和电流波形

4 结论

本文对四种主要的二维磁特性测量装置进行了有限元分析。通过比较，发现方形样片及其所对应的励磁结构在不同磁化角度上都具有最好的均匀性，但是不同方向的磁化能力不同，产生圆形旋转磁场时需要结合适当的反馈算法。而圆形样片对应的励磁结构由于齿槽效应，影响了样片的均匀性。基于分析比较，本文以方形样片为基础，提出了一种立体式高频旋转励磁装置，针对高频绕组电容效应、趋肤效应对绕组进行了改进，然后分析了磁极杂散磁场对样片均匀性的影响，提出了添加屏蔽层的方案，使样片均匀的区域几乎扩大到整个样片，提高了测量的准确性。最后，在考虑磁屏蔽层的情况下，对磁极尺寸进行了优化，采用优化后的励磁装置，励磁效果提高了36%，明显降低了对电源的要求，采用超微晶磁心的励磁装置可以将测量频率扩展到10kHz。

参考文献：

[1] 赵争菡, 汪友华, 凌跃胜, 等. 大容量高频变压器绕组损耗的计算与分析[J]. 电工技术学报, 2014, 29(5): 261-264, 270.

Zhao Zhenghan, Wang Youhua, Ling Yuesheng, et al. Calculation and analysis of loss in high-capacity high-frequency transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 261-264, 270.

[2] 张树东, 朱大为, 刘闯, 等. 交直流混合配电型通用功率变换器（UPC）研究[J]. 电力系统保护与控制, 2016, 44(1): 48-55.

Zhang Shudong, Zhu Dawei, Liu Chuang, et al. Universal power converter (UPC) for hybrid AC and DC distribution[J]. Power System Protection and Control, 2016, 44(1): 48-55.

[3] 王晓毛, 梅桂华, 谢应耿. 基于高频开关电源的反向注入式直流平衡装置的研究及应用[J]. 电力系统保护与控制, 2015, 43(8): 139-144.

Wang Xiaomao, Mei Guihua, Xie Yinggeng. Research and application of reverse injection DC- balancing device based on high-frequency switching power supply[J]. Power System Protection and Control, 2015, 43(8): 139-144.

[4] 丁茂生, 王辉, 舒兵成, 等. 含风电场的多直流送出电网电磁暂态仿真建模[J]. 电力系统保护与控制, 2015, 43(23): 63-70.

Ding Maosheng, Wang Hui, Shu Bingcheng, et al. Electromagnetic transient simulation model of multi-send HVDC system with wind plants[J]. Power System Protection and Control, 2015, 43(23): 64-70.

[5] Shen W, Ferd W, Boroyevich D, et al. High-density nanocrystalline core transformer for high-power high-frequency resonant converter[J]. IEEE Transa- ctions on Industry Applications, 2008, 44(1): 213-222.

[6] Sergeant P, Dupre L. Modeling the electromagnetic behavior of nanocrystalline soft materials[J]. IEEE Transactions on Magnetics, 2009, 45(2): 678-686.

[7] Ueno S, Todaka T, Enokizono M. Measurement of vector magnetic properties of Fe-Si-B amorphous material[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3188-3191.

[8] 李丹丹, 刘福贵, 李永建, 等. 一种新的混合矢量磁滞模型磁滞算子定义方法[J]. 电工技术学报, 2015, 30(1): 15-21.

Li Dandan, Liu Fugui, Li Yongjian, et al. A new definition of the hysteron in hybrid vector hysteresis model[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 15-21.

[9] Guo Y G, Zhu J G, Zhong J J, et al. Measurement and modeling of rotational core losses of soft magnetic materials used in electrical machines: a review[J]. IEEE Transactions on Magnetics, 2008, 44(2): 279-291.

[10] Pfutzner H. Rotational magnetization and rotational losses of grain oriented silicon steel sheets- fundamental aspects and theory[J]. IEEE Transa- ctions on Magnetics, 1994, 30(5): 2802-2807.

[11] Pfutzner H, Mulasalihovic E, Yamaguchi H, et al. Rotational magnetization in transformer cores—a review[J]. IEEE Transactions on Magnetics, 2011, 47(11): 4523-4533.

[12] Takahashi N, Mori Y, Yunoki Y, et al. Development of the 2-D single-sheet tester using diagonal exciting coil and the measurement of magnetic properties of grain-oriented electrical steel sheet[J]. IEEE Transa- ctions on Magnetics, 2011, 47(10): 4348-4351.

[13] Maeda Y, Shimoji H, Todaka T, et al. Rotational power loss of magnetic steel sheets in a circular rotational magnetic field in CCW/CW directions[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): 567-570.

[14] Ragusa C, Zurek S, Appino C, et al. An inter- comparison of rotational loss measurements in non-oriented Fe-Si alloys[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): 623-626.

[15] De la Barriere O, Appino C, Fiorillo F, et al. A novel magnetizer for 2D broadband characterization of steel sheets and soft magnetic composites[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 48(2-3): 239-245.

[16] Sievert J, Ahlers H, Birkfeld M, et al. European intercomparison of measurements of rotational power loss in electrical sheet steel[J]. Journal of Magnetism and Magnetic Materials, 1996, 160(7): 115-118.

[17] Swieboda C. Current and future use of the nanocry- stal line strips[C]//3rd International Students Conference on Electrodynamics and Mechatronics, 2011: 151-154.

[18] Brix W, Hempel K, Schulte F. Improved method for the investigation of the rotational magnetization process in electrical steel sheets[J]. IEEE Transa- ctions on Magnetics, 1984, 20(5): 1708-1710.

[19] Enokizono M, Shirakawa G, Suzuki T, et al. Two- dimensional magnetic properties of silicon-steel sheet[J]. IEEE Translation Journal on Magnetics in Japan, 1991, 6(11): 937-946.

[20] Zhang Y L, Chu X, Young H E, et al. An improved magnetic property modeling for electrical steel sheets based on double-exciting type 2D measuring system[C]// International Conference on Electrical Machines and Systems, Wuhan, 2008: 4053-4056.

[21] Zhu J G, Zhong J J, Ramsden V, et al. Power losses of soft magnetic composite materials under two- dimensional excitation[J]. Journal of Applied Physics, 1999, 85(8): 4403-4405.

[22] Makaveev D, Von Rauch M, De Wulf M, et al. Accurate field strength measurement in rotational single sheet testers[J]. Journal of Magnetism and Magnetic Materials, 2000, 215-216: 673-676.

[23] Nakano M, Nishimoto H, Fujiwara K, et al. Improve- ments of single sheet testers for measurement of 2-D magnetic properties up to high flux density[J]. IEEE Transactions on Magnetics, 1999, 35(5): 3965-3967.

[24] Mori Y, Miyagi D, Nakano M, et al. Measurement of magnetic properties of grain-oriented electrical steel sheet using 2D single sheet tester[J]. Przegląd Elektrotechniczny, 2011, 87(9b): 47-51.

[25] Hasenzagl A, Weiser B, Pfützner H. Novel 3-phase excited single sheet tester for rotational magneti- zation[J]. Journal of Magnetism and Magnetic Materials, 1996, 160(7): 180-182.

[26] De la Barriere O, Appino C, Fiorillo F, et al. Extended frequency analysis of magnetic losses under rotating induction in soft magnetic composites[J]. Journal of Applied Physics, 2012, 111(7): 07E325(1-3).

[27] Alatawneh N, Pillay P. Test specimen shape considerations for the measurement of rotational core losses[J]. IEEE Transactions on Energy Conversion, 2012, 27(1): 151-159.

[28] Makino A, Kubota T, Yubuta K, et al. Low core losses and magnetic properties of Fe85-86Si1- 2B8P4Cu1 nanocrystalline alloys with high B for power applications[J]. Journal of Applied Physics, 2011, 109(7): 07A302.

[29] Enokizono M, Suzuki T, Sievert J, et al. Rotational power loss of silicon steel sheet[J]. IEEE Transa- ctions on Magnetics, 1990, 26(5): 2562-2564.

[30] Yang Q X, Li Y J, Zhao Z H, et al. Design of a 3-D rotational magnetic properties measurement structure for soft magnetic materials[J]. IEEE Transactions on Applied Superconductivity, 2014, 24(3): 1-4.

[31] 林楠, 王东, 魏锟, 等. 高速混合励磁发电机的结构及调压性能[J]. 电工技术学报, 2016, 31(7): 19-25.

Li Nan, Wang Dong, Wei Kun, et al. Structure and voltage regulation performance of high speed hybrid excitation synchronous generators[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 19-25.

[32] Wang Y H, Yan W L, Zhang G S. Adaptive simulated annealing for the optimal design of electromagnetic devices[J]. IEEE Transactions on Magnetics, 1996, 32(3): 1214-1217.

Design and Optimization of a Magnetizer for High Frequency Rotational Magnetic Characterization for Nanocrystalline Alloy

（Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China）

Rotational core loss is widely distributed in the T-joint of high frequency transformer and the stator of high speed motor. In order to have a better understanding of such properties, rotational core loss need to be characterized accurately in high frequencies. In this paper, four different magnetizing structures have been analyzed through the finite element method. The influence of the structures on the accuracy has been discussed. A new type magnetizer for high frequency two-dimensional magnetization is developed considering the physical characteristics of nanocrystalline alloy. The yoke geometric structure is optimized, which can extend the measuring frequency up to 10kHz.

Nanocrystalline alloy, 2D rotational magnetic property, high frequency magnetizer, optimization design

TM936

国家自然科学基金（51377042），河北省高等学校自然科学青年基金（QN2016200），河北省高等学校创新团队领军人才培育计划(LJRC003)和新能源电力系统国家重点实验室开放课题（LAPS16002）资助项目。

2016-03-30 改稿日期 2016-06-26

陈 龙 男，1989年生，博士研究生，研究方向为磁性材料特性。E-mail: zhouhuoxuan@sina.com

汪友华 男，1964年生，教授，博士生导师，研究方向为电磁场数值计算和全局优化设计。E-mail: wangyi@hebut.edu.cn（通信作者）