快速高精度双站距离空间投影定位算法

2016-10-14张晓玲吴喜亮何蜀丰

电子与信息学报 2016年9期

张晓玲余檑吴喜亮何蜀丰

快速高精度双站距离空间投影定位算法

张晓玲*余檑吴喜亮何蜀丰

(电子科技大学电子工程学院成都 611731)

传统的传感器网络多目标定位方法面临的关键问题是目标与回波数据之间的匹配关联，而关联过程会带来计算量大以及如何准确提取目标的问题。基于成像策略的双站距离空间投影(Bistatic Range Space Projection, BRSP)定位算法可以有效地解决回波关联问题。然而，此算法存在运算量较大以及定位精度较低的问题。该文提出一种快速高精度双站距离空间投影(Fast and High Precision Bistatic Range Space Projection)定位算法。该算法采用分层处理，先进行低分辨率投影定位，获取目标可能区域，再以更高分辨率在目标可能区域进行投影定位，以减少运算量。然后将定位结果作为初值，构建方程组，利用泰勒级数展开算法进一步提高定位精度。仿真验证了该文所提方法的有效性，与BRSP定位算法相比，该文算法在提高定位精度的同时，相同硬件条件下定位速度可以提高数十倍，有利于实现实时定位。

传感器网络；数据关联；成像策略；分层处理；泰勒级数展开算法

1 引言

传感器网络的目标定位技术是利用分布在不同地理位置的多个传感器，对传感器回波信号的融合处理实现目标定位的技术。由于传感器网络可以获得目标从不同方位散射的回波，而空中隐身目标往往只对特定的观测角度具有隐身作用，因此传感器网络对于空中隐身目标的检测具有优势。根据测量量的不同，传感器网络定位方法也多种多样，包括基于到达时间(Time Of Arrival, TOA)[1,2]，到达角度(Angel Of Arrival, AOA)[3]，到达时间差(Time Difference Of Arrival, TDOA)，到达频差(Frequency Difference Of Arrival，FDOA)等定位方法。

传统定位方法在多目标目标定位前，必须从各个传感器的回波中区分出每个目标的对应的回波信号，才能正确建立各目标与传感器的位置方程组[10]。当传感器和目标数量增加时，可能的方程组的数量会急剧增大，解算方程组的运算量巨大，而且还存在如何从这些解中正确提取目标位置的问题[11]。

为了解决多目标与回波关联的问题，可以采用基于成像策略的投影定位方法[11]。文献[12]给出了一种基于双站距离空间投影的多目标定位方法，该方法在解决多目标定位中的回波关联问题的同时解决了投影算法带来的等价单元空变性和不规则的问题。然而该仍然算法存在两个问题：一是在整个区域投影，运算量较大，算法的实时性较差；二是目标的定位精度仍有待提高。本文分别针对上述两个问题，提出了一种快速高精度双站距离空间投影定位算法。该算法首先利用分层处理对目标进行双站空间投影定位以减小运算量，然后将最终的分层投影定位的结果作为初始值，利用泰勒级数展开定位算法进一步提高定位精度。

2 双站距离空间投影(BRSP)定位算法

2.1投影定位基本原理

从成像的角度来看，可以把传感器网络看作一个稀疏天线阵列。在此情况下，可以将成像领域的后向投影算法应用到目标定位中[13]。图1给出了多目标投影定位的示意图。

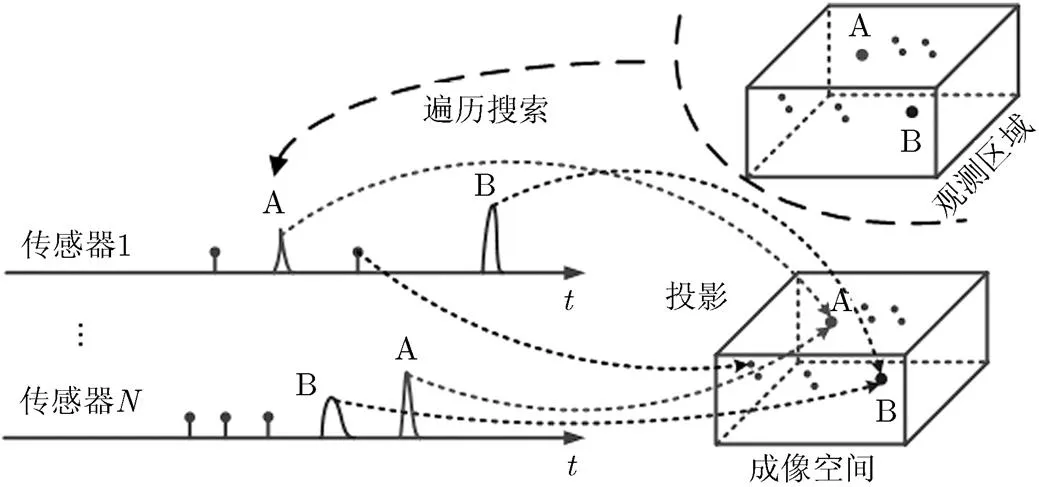
图1 多目标投影定位示意图

图1观测区域中的A, B两个目标在每个传感器中分别对应两个回波信号A和B(若目标与某个传感器距离位于该传感器接收范围以外则没有此目标的回波信息)。由于传感器可以在地面几十千米的范围内进行分布，因此不同传感器到目标的距离可能会有较大差异，从而使得两个目标回波到达不同传感器的时间先后有所不同。通过投影算法将传感器网络中的回波信息积累可以在成像空间中恢复A, B两个目标。图1中整个观测区域被划分为一组微小栅格单元，每个单元都分配一个代表点，即遍历观测区域。对于每个代表点，计算其到各个传感器的距离，利用距离取出对应的回波数据，将回波数据往成像空间中代表点所对应的像素单元进行积累，得到一幅3维图像，根据像素单元值的大小以及对应像素点坐标对目标进行定位。为了确保积累过程中各传感器所占权值相同，对回波数据的积累采用了基于目标回波的统计概率处理方法。在基于目标回波的统计概率积累的处理中，回波数据能够被表达为一个延时-概率对的集合。

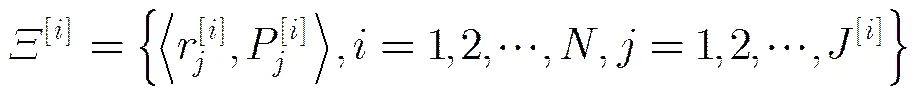
对于整个传感器网络来说，数据是不同传感器数据的集合，记作。假设传感器是互相独立的，对每个像素单元的积累可以写为式(2)的形式：

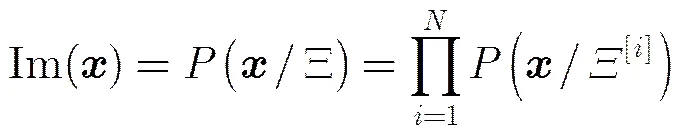
2.2 双站距离空间投影

基于成像策略的定位的一个方法是对地理空间进行投影定位，但其投影过程中会出现等价单元空变性和不规则的问题，导致定位精度较低。为了解决这个问题，文献[12]提出了一种基于双站距离空间投影的多目标定位方法。该方法将地理空间中不规则的等价单元映射为双站距离空间中规则的等价单元，映射关系定义为

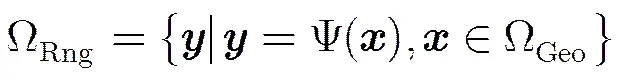
(4)

对空间进行投影成像之前，需要对成像空间进行栅格单元划分。因此完成BR空间映射后，需要对BR空间进行栅格单元划分。在BR空间中，可以对栅格单元进行式(5)所示的划分：

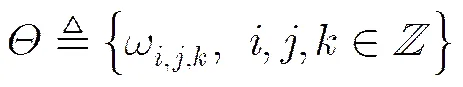
(6)

(7)

构建BR空间后，就可以利用投影算法进行成像并提取目标位置。BRSP定位算法步骤如下：

步骤 1 选择3个传感器，这3个传感器组成的三角形区域要能够包含尽可能多的传感器；

步骤 2 完成地理空间到BR空间的映射：由式(7)计算BR空间中所有的代表点，并且通过式(4)将BR空间的代表点与地理空间的坐标点建立起一一对应关系；

步骤 3 计算步骤2得到的地理空间代表点相对于一个传感器的双站距离。将此双站距离对应回波的统计概率信息往BR空间的代表点进行累加；

步骤 4 重复步骤3，直到所有传感器都被进行同样处理；

步骤 5 重复步骤3和步骤4，直到整个求解域的代表点都被处理过，最终得到一个BR空间的3维图像；

步骤 6 得到3维图像后，利用贪婪清除算法，提取目标位置。

3 快速高精度双站距离空间投影定位算法

通过上节分析可以看出，BRSP定位算法需要遍历整个BR空间的代表点才能进行成像，因此运算量较大。而且基于成像策略的定位算法不能很好解决模糊区域问题，因此算法定位精度仍有待提高。本文采用分层处理的方法进行投影定位以减少运算量，并结合泰勒级数展开的定位算法从而实现更高精度的定位。

3.1基于分层的双站距离空间投影定位算法

分层处理，从本质上来说是一种多分辨率逼近的方法。主要思想是先以低分辨率进行投影定位，得到目标可能存在的区域，在目标的可能区域以更高的分辨率进行下一次的投影定位，直到投影分辨率达到系统分辨率为止。这样就能以较低的运算量实现对目标的定位。BR空间投影定位算法的分层处理的示意图如图2所示。

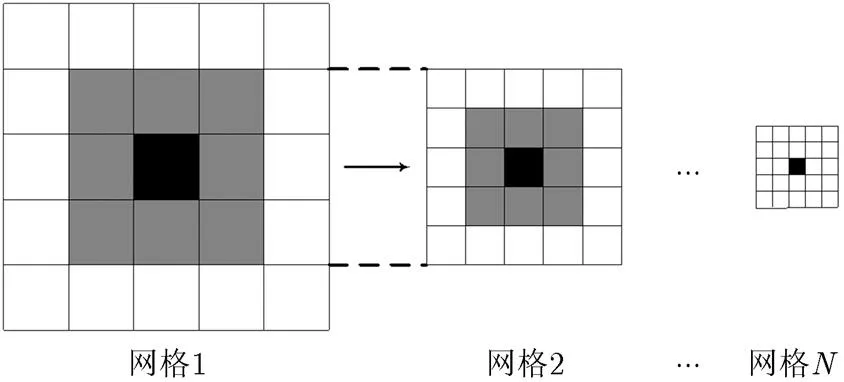
图2 分层处理示意图

首先，以较大的间隔划分栅格单元并进行投影成像，得到低分辨率的图像网格1。然后在该图像中找到目标可能存在的栅格单元，即网格1中的黑色单元，再以该栅格单元为中心，取出与其相邻的区域作为目标可能存在的区域进行下一层划分。再以更小的栅格单元划分利用从网格1中取出区域中的回波信息进行投影成像，得到网格2。以此类推，得到网格。作为最后一次网格划分，网格的栅格单元间隔应该与系统分辨率一致，黑色区域为目标的定位结果。

在分层处理中，每层分辨率按照2倍数扩张，即若总共划分层数为层，则第层分辨率为。对于一个在系统分辨率下有个栅格单元的场景来说目标在场景空间占据的栅格单元总数为

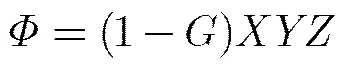
(9)

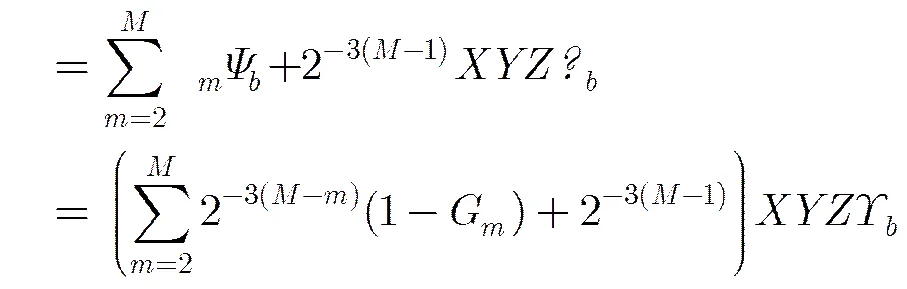
在进行低分辨率成像时，需要对每层的回波数据进行整合，以适应当前分辨率。每个传感器回波的采样间隔应当与距离分辨率一致。假设系统分辨率为，降分辨率为(是大于1的整数)，则为了保证采样间隔为，回波数据中每个相邻的回波单元要合并成一个单元，从而构建一个新的回波数据。由2.1节分析可知，对回波数据的积累采用了基于目标回波的统计概率处理方法，故相邻距离门整合后的回波可表示为

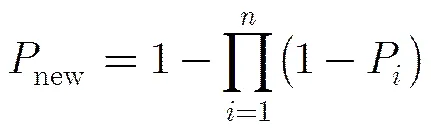
步骤 1 根据划分层次，确定第1次网格划分的栅格单元大小；

步骤 2 根据栅格单元的大小对回波进行降分辨率处理，得到新的回波数据；

步骤 3 以步骤2中栅格单元为基础进行BR空间投影定位，得到目标位置信息；

步骤 4 判断本次划分的分辨率是否等于系统分辨率。如果是则算法结束得到定位结果，否则选取目标及其相邻栅格单元的数据，以更高的分辨率转到步骤2。

3.2基于泰勒级数展开的定位算法

上节采用分层处理，以多分辨率逼近的方式减小了投影定位算法的运算量，但是仍然不能解决成像策略定位算法带来的模糊区域问题，定位精度仍有待提高。本节将3.1节所提出算法得到的定位结果与基于泰勒级数展开的定位算法相结合，以提高目标的定位精度。

基于泰勒级数展开的定位算法[15]是一种迭代方法，算法收敛性受初始值的影响，3.1节算法定位精度在10 m左右，因此以3.1节算法的定位结果作为泰勒级数展开定位算法的初始值能够确保算法的收敛性。算法思想如下：

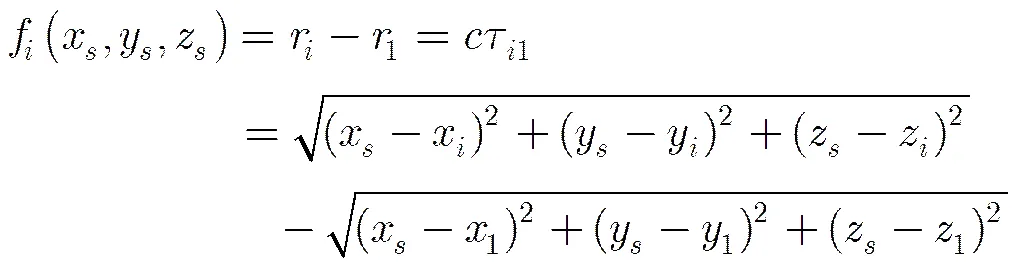
对式(12)进行一阶泰勒展开可得：

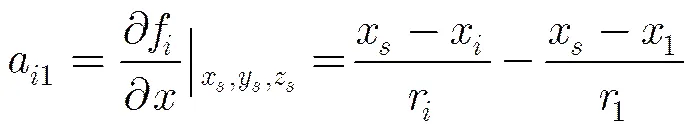
(14)

(15)

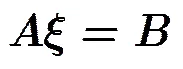
(17)

(18)

得到式(16)-式(18)后，利用最小二乘法[16]计算修正向量并对目标位置进行修正：,,。基于泰勒级数展开的定位算法步骤如下：

步骤 3 重复步骤1和步骤2，直到所有的传感器都进行了处理；

步骤 4 联合得到的方程，建立方程组。计算修正向量并对目标位置进行修正；

步骤 6 判断是否所有目标都进行处理，如果是则算法结束，否则选取新的目标位置转到步骤1。

综上所述，可得本文提出的快速高精度双站距离空间投影定位算法流程如图3所示。

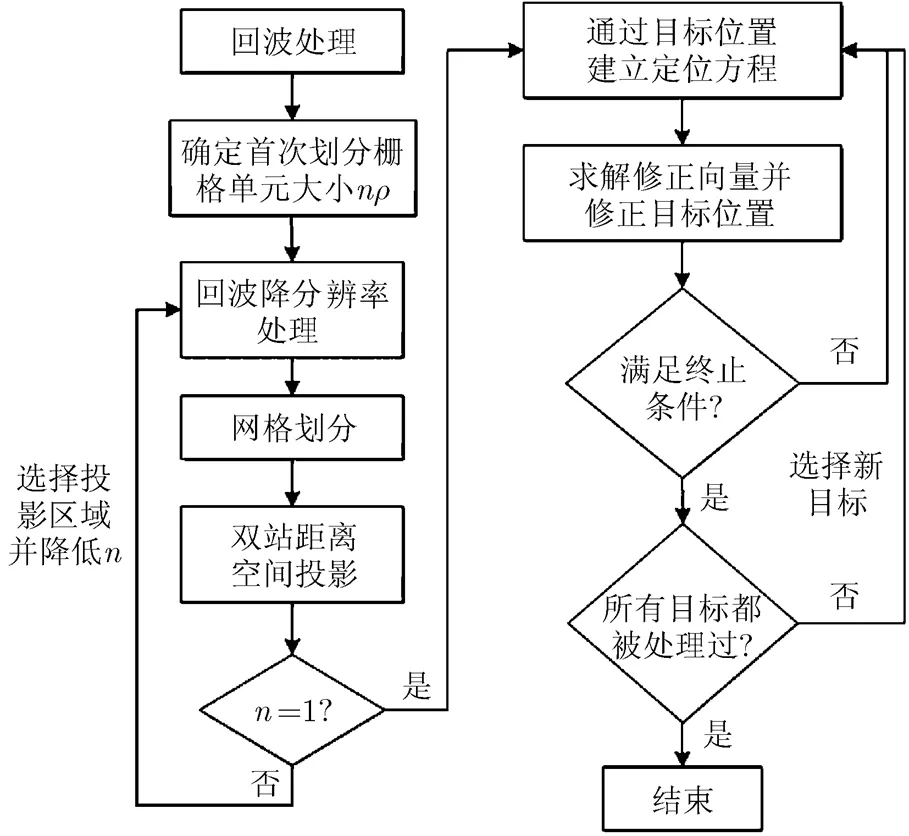
图3 快速高精度双站距离空间投影定位算法流程图

4 仿真分析

本文通过仿真，将BRSP定位算法与本文所提出的快速高精度双站距离空间投影定位算法作为比较，验证本文所提算法的有效性。仿真参数设置如下所示：

发射机放置在[0, 0, 0] km处，传感器有3个位于[25, 0, 0] km, [-25, 0, 0] km和[0, 43, 0] km，剩余传感器分布在以这3个传感器为顶点的三角形区域内。目标随机分布在以[5, 5, 10] km为中心的附近区域，为了验证对不同情况下目标定位的有效性，目标的散射系数在1到30之间随机取值。分层处理时总共分为了4层，栅格单元的划分间隔分别为80 m, 40 m, 20 m, 10 m。

BRSP定位算法与本文所提算法的定位结果分别如图4和图5所示。其中，符号“”表示定位结果，符号“＋”表示目标实际位置。

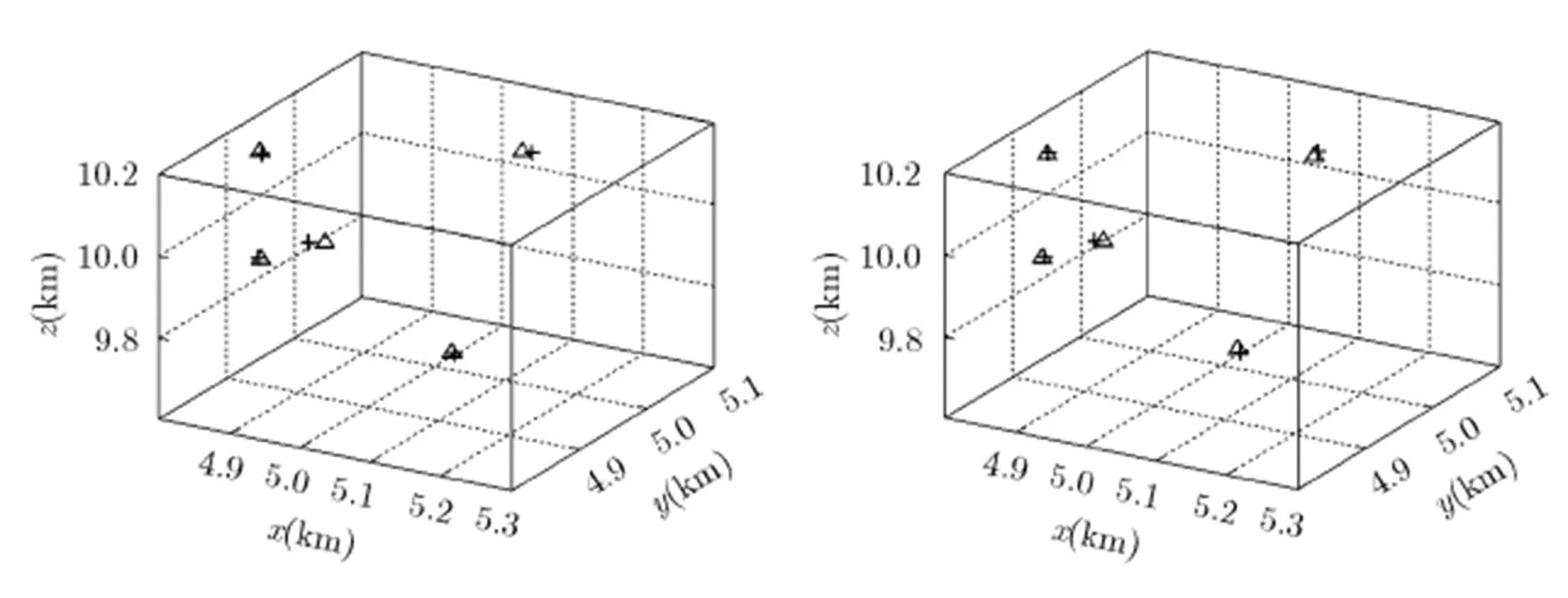
图4 BRSP定位算法定位结果图5 本文算法定位结果

表1列出了各目标在1000次蒙特卡洛仿真下的定位均方根误差，相同硬件条件下两个算法1000次蒙特卡洛仿真平均运行时间如表2所示。

表2 本文算法与BRSP定位算法的平均定位时间对比(s)

对比图4和图5，以及从表1和表2可以看出，与BRSP定位算法相比，本文提出算法首先通过分层处理在不损失定位精度的情况下减少了投影定位所需要的计算单元，大幅度缩短了算法定位时间；其次由于泰勒级数展开定位算法的引入，将投影定位得到的结果作为初值迭代修正了定位误差，从而提高了算法的定位精度。

考虑到实际定位中传感器自身位置信息存在一定误差，本文在以上仿真条件下加入了1~15 m的传感器位置误差进行仿真。不同传感器位置误差下分别进行了1000次蒙特卡洛仿真实验。两种方法的仿真结果对比如图6所示。其中，纵坐标为所有目标均方根误差的平均值。

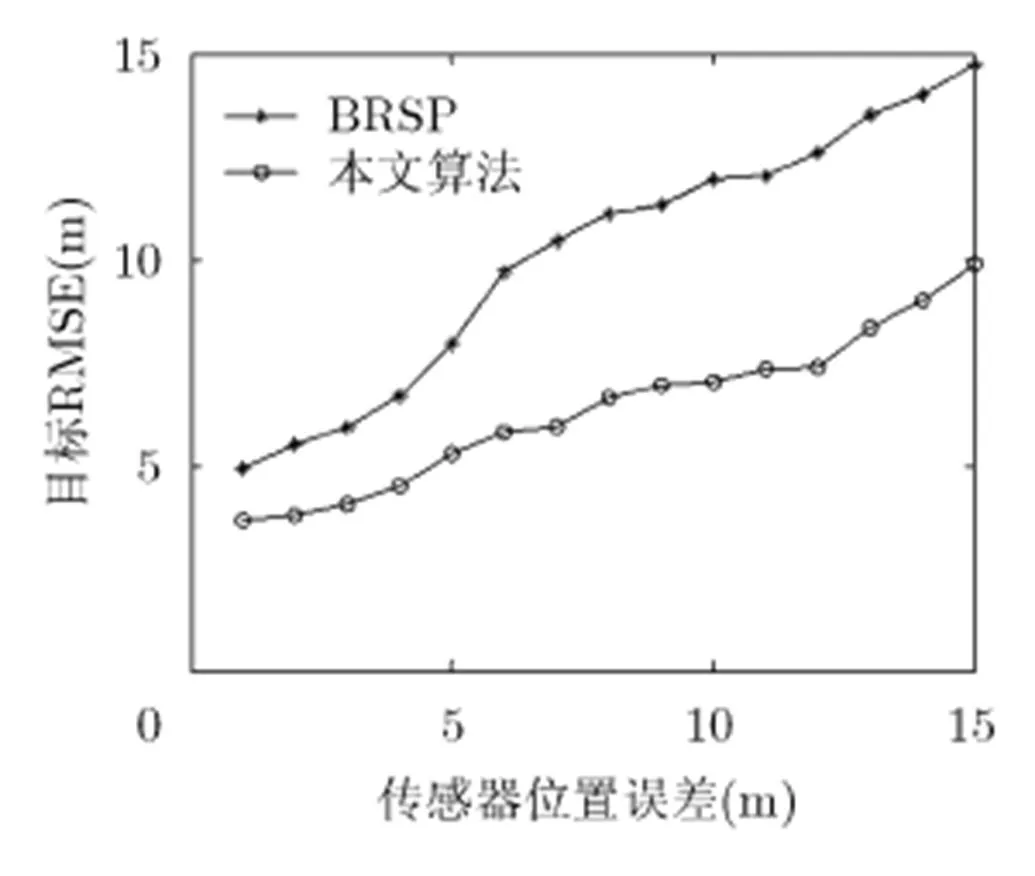
图6 不同传感器位置误差下两种方法定位精度对比

从图6可以看出，在传感器位置误差较大的情况下本文算法仍能保证较高的定位精度。

5 结束语

本文算法采用了分层策略，对目标位置进行多分辨率逼近，有效解决了基于成像的定位算法需要遍历整个成像空间而带来的运算量过大问题。将基于成像策略的定位算法与时差定位算法相结合，不仅解决了数据关联问题，而且提高了算法定位精度。相比已有基于成像策略的定位算法，本文所提的算法不但提高了算法定位精度还大幅度缩短了算法定位时间。并且在传感器位置误差较大的情况下仍能保证较高的定位精度。

[1] HONG Shen,ZHI Ding, SOURA D,. Multiple source localization in wireless sensor networks based on time of arrival measurement[J]., 2014, 62(8): 1938-1949. doi: 10.1109/TSP.2014. 2304433.

[2] CHAN Y T, HANG H, and CHING P C. Exact and approximate maximum likelihood localization algorithms[J]., 2006, 55(1): 10-16. doi: 10.1109/TVT.2005.861162.

[3] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280. doi: 10.1109/TAP. 1986.1143830.

[4] MENG Wei, XIE Linghua, and XIAO Wendong. Decentralized TDOA sensor pairing in multihop wireless sensor networks[J]., 2013, 20(2): 181-184.doi: 10.1109/LSP.2013.2237823.

[5] XIONG Hui, CHEN Zhiyuan, YANG Beiya,. TDOA localization algorithm with compensation of clock offset for wireless sensor networks[J].,2015, 12(10): 193-201.doi: 10.1109/CC.2015.7315070.

[6] NARESH V, STEVEN K, and QUAN Ding. TDOA based direct positioning maximum likelihood estimator and the cramer-rao bound[J]., 2014, 50(3): 1616-1635. doi: 10.1109/ TAES.2013.110499.

[7] ZHU Guohui and FENG Dazheng. Bi-iterative method for moving source localisation using TDOA and FDOA[J]., 2015, 55(1): 8-10. doi: 10.1049/el.2014. 2386.

[8] MOHAMMAD P and MARK L F. Distributed computation for direct position determination emitter location[J]., 2014, 50(4): 2878-2889.doi: 10.1109/TAES.2014.130005.

[9] YANG Kehu and LUO Zhiquan. Robust target localization with multiple sensors using time difference of arrivals[C]. IEEE Radar Conference, Rome, 2008: 1080-1085. doi: 10.1109/RADAR.2008.4720928.

[10] 房嘉奇, 冯大政, 李进. 稳健收敛的时差频差定位技术[J]. 电子与信息学报, 2015, 37(4): 798-803. doi: 10.11999/JEIT 140560.

FANG Jiaqi, FENG Dazheng, and LI Jin. A robustly convergent algorithm for source localization using time difference of arrival and frequency difference of arrival[J].&, 2015, 37(4): 798-803. doi: 10.11999/JEIT140560.

[11] SHI Tongyan, ZHANG Xiaoling, and SHI Jun. Multi-target positioning for sensor network based on imaging strategy[C]. International Conference on Computational Problem- Solving, Jiuzhai, 2013: 171-174. doi: 10.1109/ICCPS.2013. 6893549.

[12] SHI Jun, FAN Ling, ZHANG Xiao-ling,. Multi-target positioning for passive sensor network via bistatic range space projection[J]., 2016, 59(1): 1-3 doi: 10.1007/s11432-015-5464-x.

[13] HONG I K, CHUNG S T, KIM H K,. Fast forward and backward projection algorithm using SIMD[C]. Nuclear Science Symposium Conference Record, San Diego, 2006: 3361-3368. doi: 10.1109/NSSMIC.2006.353723.

[14] SHI Jun, ZHANG Xiaoling, YANG Jianyu,. APC trajectory design for “one-active” linear-array three- dimensional imaging SAR[J]., 2010, 48(3): 1470-1486. doi: 10.1109/TGRS.2009.2031430.

[15] WADE H F. Position-location solutions by Taylor series estimation[J]., 1976, 12(2): 187-194. doi: 10.1109/ TAES.1976.308294.

[16] CHAN Y T and HO K C. A simple and efficient estimator for hyperbolic location[J]., 1994, 42(8): 1905-1915. doi: 10.1109/78.301830.

Fast and High Precision Multi-target Positioning via Imaging Strategy

ZHANG Xiaoling YU Lei WU Xiliang HE Shufeng

(School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

The association between multiple targets and echo data is the main problem for multi-target location method, which causes huge calculation and the problem of extracting the targets accurately. The location method based on Bistatic Range Space Projection (BRSP) can be used for the sake of overcoming the data association problem. While there are two problems existing on the location method of BRSP, the huge calculation and the low resolution. In the face of vast calculation in projection imaging localization, this paper utilizes hierarchical strategy to decrease calculation. The possible targets areas are located with low resolution at first. After that, more precision probable areas are pinpointed via higher resolution from these possible areas. In this way, the calculation of areas without targets can be avoided. Furthermore, results of hierarchical processing are used to be the initial position guess for Taylor-series estimation. Positioning errors could be modified by the iterative correction of Taylor-series estimation. Simulation results indicate a significant improvement in the running time and positioning precision of the proposed method.

Sensor network; Data association; Imaging strategy; Hierarchical strategy; Taylor series expansion algorithm

TN971

1009-5896(2016)09-2330-06

10.11999/JEIT151315

2015-11-25；

2016-04-13；

2016-05-31

航空科学基金(20130180001, 20142080007)

Aeronautical Science Foundation of China (20130180001, 20142080007)

张晓玲 txlzhang@163.com

张晓玲：女，1964年生，教授，博士生导师，主要研究方向为雷达系统信号处理、雷达成像及目标识别.

余檑：男，1992年生，硕士生，研究方向为雷达系统信号处理.