利用两阶段遗传算法的机械手最优轨迹控制仿真

龚畅，王华君，李荣，徐平平



利用两阶段遗传算法的机械手最优轨迹控制仿真

龚畅，王华君，李荣，徐平平

针对大多数机器人最优轨迹规划控制算法成本较高的问题，提出了一种两阶段分析-进化算法，分析算法基于间接开环最优控制问题，进化算法基于遗传算法。首先，利用遗传算法产生最优控制；然后，新的次优轨迹通过最优控制生成，计算每个最优解的成本函数，并为下一个步骤选择最优解做准备；最后，遗传算法使用获得的轨迹产生新一代起始点，迭代直到实现最小成本值。算法的验证由两个仿真系统组成：具有完整约束的两关节机械手和具有非完整约束的移动机械手。运用本文算法后，第一个仿真系统的成本降低了92.3%，第二个仿真系统获得的最优成本明显低于只使用最优控制时的成本，表明其算法可应用于实际机器人轨迹规划控制系统。

机器人；移动机械手；最优轨迹控制；分析-进化；两阶段遗传算法

0 引言

机器人最优轨迹规划控制[1,2]在越来越发达的人工智能和制造业等领域占有重要地位，但通常需要花费较高的成本，因此，找到一种能够降低成本的轨迹规划算法显得非常重要[3,4]。

已经有很多学者对机器人最优规划控制进行了研究。文献[5]考虑机器人各关节速度、加速度和力矩约束，在末端执行器和任给轨迹下进行时间最优规划，采用遗传算法和动力学方程缩短了规划时间，然而，动力学方程和遗传算法简单的结合并不能保证结果大多数情况下正确。

文献[6]引入了一种方法，使用路径参数的三阶导数确定机械手的平滑和时间最优路径，通过在转矩率上施加限制得到轨迹所需的光滑度，使用可变容差法求解最优问题。虽然该方法可以返回一个局部最小值，但不适用于整个系统。

文献[7]为二阶欠驱动机械系统提出了一种利用运动学可控概念的轨迹规划，可以获得一个最佳的时间解，然而，却忽略了其他路径参数。

本文提出一种两阶段分析-进化算法，可分析动力学方程，采用最优控制，搜索所有可能的起始点，实现具有最小成本的轨迹。进化过程基于遗传算法[8]，定义新选择算子来为交叉运算选择合适的轨迹，实现了全局最优控制，具有非完整约束的系统适用性。

1 算法架构

根据导致两点边值问题的间接最优控制，提出两阶段迭代算法以获得全局最优轨迹，为了启动该算法，使用初始猜测有两个目的：（a）作为起始点求解最优控制，（b）作为GA的第一个种群。算法的整体架构如图1所示：

定义成本函数之后，得到最优控制的必要条件，采用这些必要条件来寻找最佳控制输入[9]。

2 算法详细设计

提出的轨迹规划控制算法的详细流程如图2所示：

第一阶段优化控制所用状态的起始点由GA生成，然后通过最优控制，完成优化的第二阶段，并产生具有低成本函数的新路径。由于最优控制可能会陷入局部最优解，产生的路径发送到GA，用于生成起始点，并开始迭代新步骤，这个过程一直持续到实现最低成本函数。本文算法包括4个主要步骤：（1）推导动力学方程；（2）求解最优控制，并开发TPBVP；（3）由GA生成最优控制起始点，反之亦然；（4）停止条件（最低成本并不随着迭代周期变化）。

2.1 最优控制

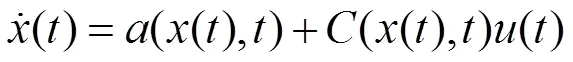
（2）

（4）

最优控制解(此处由*表示)必须满足必要条件如公式（6）-（9）：

（6）

（8）

（9）

因此，根据式（8），最优条件可通过相对于状态、合作状态和控制微分哈密顿函数得到，如公式（11）~（13）：

（11）

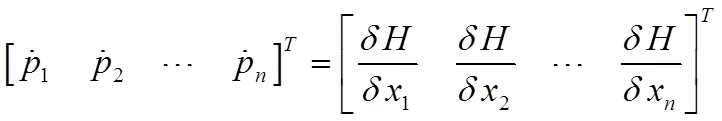
（13）

2.2 利用GA产生起点

为了满足上述问题，采用遗传算法来产生最优控制方法中合适的起点。边值问题（Boundary Value Problem，BVP）[10]可用不同软件包的有效命令求解，数据包用数值方法来解决这个问题，数值方法需要起始点（或初始解），但由于对起始点敏感，导致边值问题不可靠，它可能会陷于局部最小值[11]，GA提供起始点，检查起始点，并选择最佳起始点。起始点由下式给出公式（15）：

2.3 编码

即每行表示每个状态，正比于时间，如公式（17）、（18）

（17）

系数可以包含任意位数，这里系数由8位数字表示，第一组4位用作系数的整数部分，第二组用作系数的小数部分。为了操作这些数字，以位定位每个数字，第九位表示正或负，如果数字为正，该位将是“1”，如果数字为负，该位将是“0”。编码示例如图3所示：

2.4 选择算子

选择算子是用于交叉操作的适合染色体的选择，越合适的染色体，选择它的概率就越大。为了选择配对染色体，首先选择一些低成本染色体，假设选择了个染色体，每个染色体的重复数对应于式（19）。由于最低成本非常重要，新成本函数根据式（20）定义，如公式（19）、（20）：

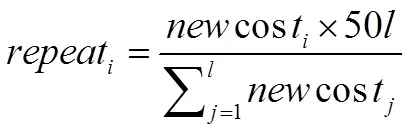
（20）

现在，虚拟空间有50l个房间，每个染色体复制自身重复数次，并占据房间。假设交叉数等于n，则随机选择2n个房间，从而，选择房间中的2n个染色体进行交叉操作。应当指出的是，因子“50”只是为了提高选择数，从而提高染色体选择的精确度，它可以为任意数。例如，假设n=2，l=4，每个染色体的成本和索引如表1所示：

表1 重复函数示例

根据图4所示：

考虑到每个染色体的重复函数的数目，从房间中选择4（或2）个，最后，如表2所示：

表2 选择的配对染色体

2.5 交叉

使用两点交叉，以便选择点的整数和小数部分，点随机选择。通过选择算子选择两个染色体后，一起替代选择的染色体的全部系数的位，从第一点到第二点。交叉运算的示例如图5所示：

2.6 突变

突变意味着33%的染色体应用于交叉，选择每个染色体33%的状态，然后，选择多项式的两个系数，从系数中选择一个数字，改变为另一个，所有选择随机进行。突变的示例如图6所示：

3仿真实验

3.1 仿真系统1：2关节机械手

第一个系统是2关节机械手如图7所示：

物理参数由文献[5]给出，如表3所示：

表3 两关节机械手的物理参数

这个例子中，不存在对控制输入的任何约束，文献[5]是能量最优轨迹规划，最终时间=1秒，初始条件是，最终条件是。权重为，（限制权重）=1，且=1。虽然该系统有完整约束，哈密顿定义为公式（31）：

关节扭矩如图8所示：

（a）关节扭矩

（b）末端执行器的轨迹

（c）每一次迭代中的最小成本

图8 关节机械手仿真结果

图8（a）所示为关节扭矩，扭矩比文献[5]算法少，表明了本文算法的有效性。图8（b）表示轨迹上机械手配置，图8（c）表示每一次迭代中的最小成本，如第一次迭代中最小成本约为1180，最后一次迭代为721，停止条件是50次迭代下最低成本不改变。

3.2 仿真系统2：非完整约束移动机械手

第二个仿真系统是3关节(PUMA)机械手[12]，环境中有障碍物，如图9所示：

表4 WMM参数和惯性特性

状态向量定义如公式(32)：

（a）中心轴线相对于平台的角位置

（b）机械手关节扭矩

（c）车轮扭矩

（d）轨迹内移动机械手

（e）每次迭代中的最低成本

图10 -关节移动机械手仿真结果

10（a），关节和车轮随时间的关节扭矩值如图10（b）和10（c）所示。最优控制模式中转矩值非常大，不能与组合最优控制模式相媲美。图10（d）是环境中机器人的轨迹，说明本文算法适用于有障碍的环境。图10（e）是每次迭代的最小成本。结果表明，由最优控制生成的轨迹不唯一收敛于全局最佳轨迹，但本文算法在86次迭代后得到全局最小值。

在仿真系统2中，本文算法获得的最优成本是5.5e-4，而仅最优控制获得的成本为1.8e-3。该算法可以用于包括障碍物的环境，还可用于具有完整和/或不完整约束的系统。

3.3 时间复杂度分析

GA搜索所有可能解以获得最优路径。本文使用进化和分析方法的优点，提出双阶迭代公式。引入遗传算法新算子，以减少所需要的时间。第一阶段优化控制所用状态的起始点由GA生成，然后通过最优控制，完成优化的第二阶段，并产生具有低成本函数的新路径。这个过程涉及迭代次数和GA算法的变量，其时间复杂度大约为，其中和分别为多项式阶次和状态数，k为达到要求的迭代次数或最高迭代次数，仿真实验中，对于两机械手k=50，对于三机械手，k=86。

4 总结

本文提出了寻找全局最优轨迹规划的新算法，即基于遗传算法和间接最优控制，同时考虑了动力学方程。最优控制的分析属性允许动力学方程具有适当接口，利用GA搜索所有可能解获得最优轨迹。本文使用进化和分析方法的优点，提出新的双阶迭代公式。此外，引入遗传算法新算子，以减少所需要的时间。仿真结果表明，本文算法明显降低了最低成本，即使在有障碍物的情况下依然表现良好，该算法可以应用于实际的机器人轨迹规划控制系统，因为两关节和三关节机械手是机器人的必要装置，而且处理有障碍物和较低的轨迹规划时间也是实际机器人轨迹控制系统的特点。

参考文献：

[1] 彭建盛, 李兴, 秦志强等. 智能机器人仿真系统设计[J]. 计算机仿真, 2013, 30(5): 358-361.

[2] 徐文福, 李成, 梁斌等. 空间机器人捕获运动目标的协调规划与控制方法[J]. 自动化学报, 2009, 35(9): 1216-1225.

[3] 张雨浓, 陈锦浩, 劳稳超等. 多类单输入多项式神经网络预测能力比较[J]. 系统仿真学报, 2014, 26(1): 1047-1053.

[4] Nayl T, Nikolakopoulos G, Gustafsson T. Real-Time Bug-Like Dynamic Path Planning for an Articulated Vehicle[C]//Informatics in Control, Automation and Robotics. Springer International Publishing, 2015: 201-215.

[5] Ulusoy A, Smith S L, Belta C. Optimal Multi-robot path planning with LTL constraints: guaranteeing correctness through synchronization[C]//Distributed Autonomous Robotic Systems. Springer Berlin Heidelberg, 2014: 337-351.

[6] Saijo H, Kuroki Y. Articulated robot and method of controlling the motion of the same[D]. US, 2001.

[7] Shiriaev A S, Freidovich L B, Spong M W. Controlled Invariants and Trajectory Planning for Underactuated Mechanical Systems[J]. IEEE Transactions on Automatic Control, 2014, 59(9):2555 - 2561.

[8] 于海璁, 陆锋. 一种基于遗传算法的多模式多标准轨迹规划方法[J]. 测绘学报, 2014, 27(1): 89-96.

[9] Zhou Z, Zhang Z, Luo X. A Fuzzy Path Preview Algorithm for the Rice Transplanting Robot Navigation System [J]. Journal of Software, 2014, 9(4): 881-888.

[10] 周文卷. 复杂环境下自主移动机器人轨迹规划方法的研究[D]. 吉林大学, 2014.

[11] 李国勇, 闫芳, 郭晓峰. 基于遗传算法的灰色神经网络优化算法[J]. 控制工程, 2013, 20(5): 934-937.

[12] Gregory J, Olivares A, Staffetti E. Energy-optimal trajectory planning for robot manipulators with holonomic constraints [J]. Systems & Control Letters, 2012, 61(2): 279-291.

Simulation of Optimal Trajectory Planning Controlling for Moving Manipulator Using Two-stage Analysis-evolutionary Algorithm

Gong Chang1, Wang Huajun1, Li Rong1, Xu Pingping2

(1. School of Engineering, Taihu University of Wuxi, Wuxi 214064, China;2. School of Information Science and Engineering, Southeast University, Nanjing 211189, China)

As the problem of high cost in optimal manipulator trajectory planning algorithm, a two-stage analysis-evolutionary algorithm is proposed. The analysis algorithm is based on indirect open-loop optimal control problem. The evolutionary algorithm is based on Genetic algorithm (GA). Firstly, the starting point of optimal control problems results from the optimal solution by GA. Then, a new sub-optimal path is generated by the optimal control, and the cost function of every optimal solution is calculated, preparing for the next step to choose the optimal solution. Finally, the new starting point is obtained by the new generation of the path using GA. The iteration is ended until the minimum cost value can be obtained. Verification algorithm simulation system consists of two components, a system is a two-joint mobile manipulator with a complete constraint, and the other is a mobile manipulator with a non-complete constraint. By using the proposed algorithm, the cost of the first simulation system reduces 92.3%, and the optimal cost of a second simulation system is clearly less than that of only using optimal controlling. Simulation results show that the algorithm can be applied to any robot path planning.

Robot; Moving Manipulator; Optimal Trajectory Control; Analysis-evolutionary; Two-stage Genetic Algorithm

1007-757X(2016)04-0018-05

TP242.2

A

（2015.09.11）

江苏省高校自然科学研究项目（14KJB520036）

龚 畅（1981-），女（汉），海门人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人、人工智能等，无锡，214064

王华君（1979-），男（汉），宜兴人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人、模式识别等，无锡，214064

李 荣（1978-），女（汉），江苏淮安人，无锡太湖学院，工学院，讲师，硕士，研究方向：机器人控制、人工智能等，无锡，214064

徐平平（1957-），女（汉），南京人，东南大学，信息科技与工程学院，教授，博导，博士，研究方向：机器人控制、物联网等，南京，211189