基于解析解和修正Newton-Raphson法的土层固结参数反分析研究
2016-10-14黄大中
黄大中
(铁道第三勘察设计院集团有限公司,天津 300251)
基于解析解和修正Newton-Raphson法的土层固结参数反分析研究
黄大中
(铁道第三勘察设计院集团有限公司,天津300251)
土体固结参数的准确性是影响土层沉降变形计算精度的重要因素,常规室内试验获得的土体固结参数受扰动较大,精度无法满足精确计算需求。基于土层固结解析解和修正Newton-Raphson方法,建立通过土层沉降变形监测值反分析土层固结参数的优化求解模型,实现了对土体固结参数(体积压缩系数、渗透系数)和初始固结时间的准确估计,可满足工程中准确预测土层沉降变形随时间发展变化的需求。
解析解Newton-Raphson法固结参数反分析
岩土工程中计算上部堆载、地下水位下降引发的土层沉降变形需要利用土体的固结参数,包括体积压缩系数mv和渗透系数k,土体固结参数值的准确性直接影响土层沉降变形计算的精度。目前,土体的固结参数主要通过室内压缩和渗透试验确定[1-2],由于土样在钻取、运输和试验操作过程中易受扰动,因此室内试验测定参数值与实际值往往存在较大的误差,无法准确反映实际工程状况[3-5]。
反分析是当前岩土工程研究的一个重点领域,提供了获取岩土参数的一条新途径[6-7]。针对土层固结问题,很多学者利用现场实测的沉降量对固结系数cv进行反演计算,包括图解法、最小二乘法、Asaoka法、遗传算法等[8-11]。固结系数是由体积压缩系数和渗透系数计算得出的综合性指标,只能反映土层固结发展趋势,无法用于土层沉降值计算。另外,由于沉降监测的初次记录时间与起始固结时间常常存在一定时间间隔,沉降监测记录时间点相比真实的固结时间点存在一定的误差。综上所述,目前尚未有根据土层沉降变形监测值对土层体积压缩系数、渗透系数和初始固结时间3个指标同时进行反分析的研究。
利用土层沉降变形监测值,建立能综合反映各时间点下沉降监测权重的目标函数,结合土层固结解析解,利用修正Newton-Raphson方法对体积压缩系数、渗透系数和初始固结时间进行优化反演。算例应用表明,建立的反演分析模型具有良好的收敛性,能够得出符合实际的土体固结参数值,可以进一步用于预测以后的土层沉降发展状况。
1 土层固结解析解
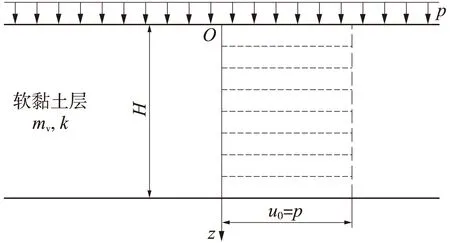
图1 大面积荷载引发的土层固结示意
由大面积荷载引发的土层固结如图1所示,土层上部受荷载p作用,上下表面透水,初始超静孔隙水压力均匀分布为p,土层厚度为H,体积压缩系数为mv,渗透系数为k。
土层在荷载作用下固结问题的控制方程为
(1)
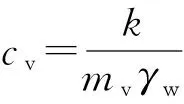
根据边界条件可求得土层表面沉降变形的解析解[12]
(2)
式中,M=(2n-1)π,n=1,2,3,…。
由区域地下水位下降引发的土层固结如图2所示,土层上部含水层(潜水层)水位恒定不变,初始时刻土层下部含水层(承压层)水位下降量为hc,土体厚度为H,体积压缩系数为mv,渗透系数为k。
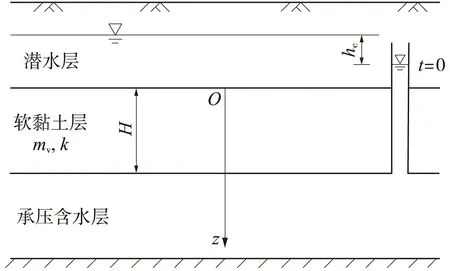
图2 水位下降引发的土层固结示意
土层由水位下降引发的固结问题控制方程与式(1)一致,根据边界条件可求得土层表面沉降变形的解析解为[13]
(3)
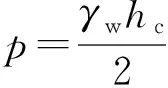
假定对土层沉降开始进行监测记录时,土层已发生固结的时间为t0,则土层的沉降表达式为
(4)
式中,t为监测记录时间。
2 固结参数反分析模型
根据沉降监测数据反演土体固结参数及初始固结时间时,需要设定合理的目标函数。为充分体现各个时间点下沉降值的权重,设定反分析的目标函数为
(5)
式中,s为按式(4)计算得出的沉降值;si为ti时刻土层的沉降量监测值;N为监测值记录数。
对土层固结参数进行反分析的目标为求解一组参数值mv,cv,t0,使得目标函数值最小,随着目标函数值接近于0,反分析结果与实际越趋于一致。求得参数值mv,cv后,可计算渗透系数k=cvγwmv。
由于目标函数为非线性函数,需要采用迭代方式对其进行求解,本模型中采用了效率较高的Newton-Raphson法[14],并在迭代过程中沿其迭代方向进行一维搜索,确定合理的迭代步长。
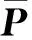
(6)
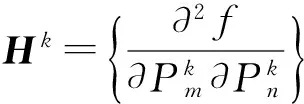
目标函数的一阶导数和二阶导数可表示为
(7)
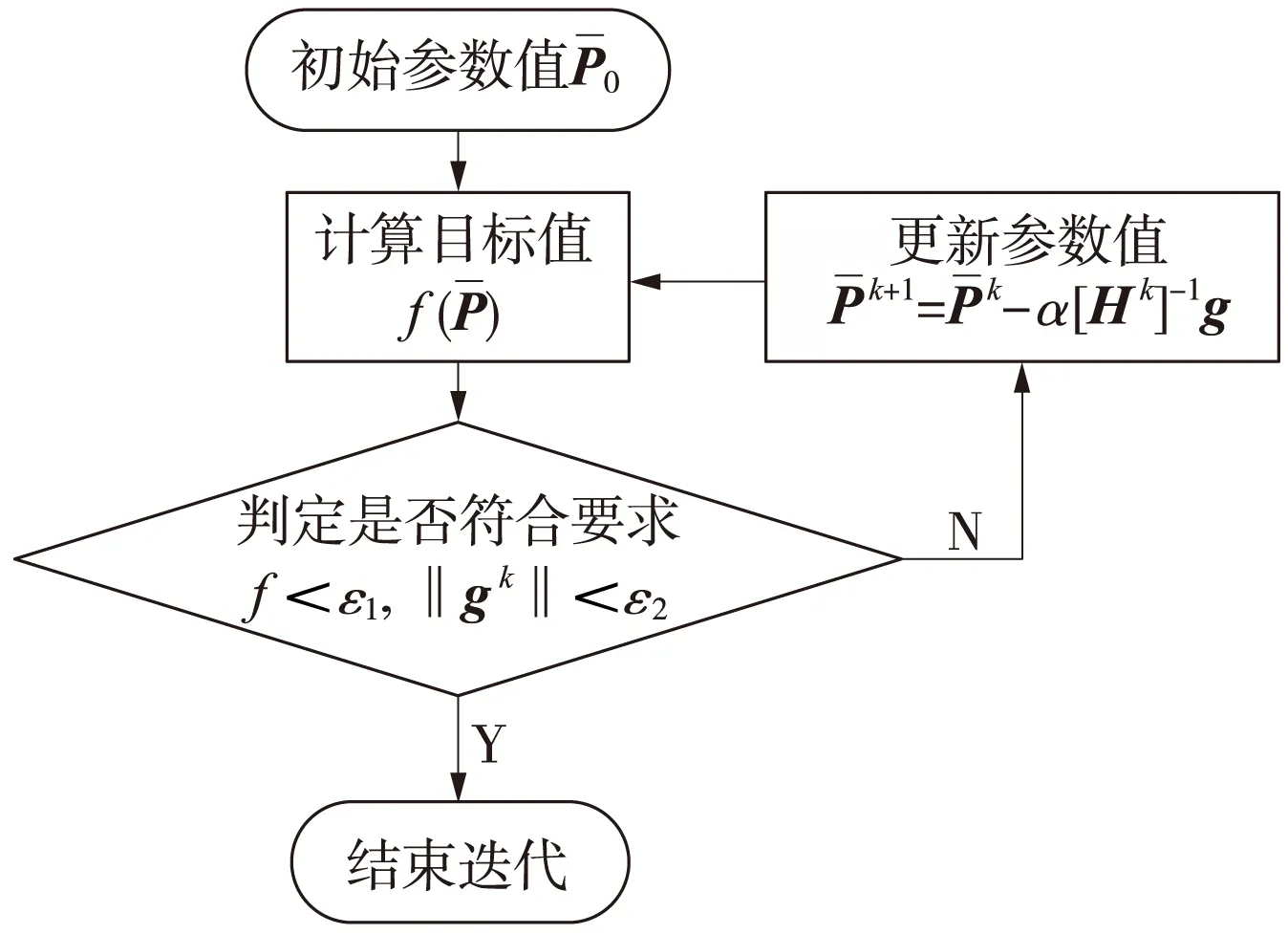
图3 固结参数优化求解流程
3 算例分析
某地区由于超采地下水,导致地下水位发生大面积下降,下降量为20m,软黏土层的厚度为15m,对软黏土层沉降变形的观测记录如表1所示。

表1 土层沉降量监测值
假定软黏土体积压缩系数mv为0.1MPa-1,渗透系数k为1×10-7m/s,初始记录时已固结时间t0为0.5d,则固结系数cv为10-4m2/s。根据沉降量监测数据对土层固结参数进行反演计算,图4所示为目标函数值在反演过程中的变化情况。可以发现,随着迭代过程,目标函数值迅速变小,最终接近于0,说明反分析过程是收敛的,各时间点下土层沉降计算结果与监测结果逐渐接近。
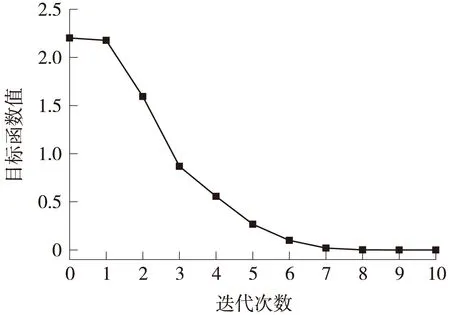
图4 目标函数值迭代变化情况
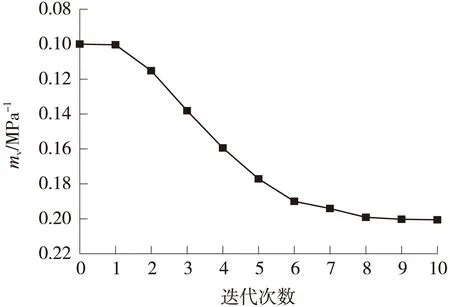
图5 体积压缩系数mv迭代过程
各参数反演过程中的变化情况如图5~图7所示,可以看出,随着迭代的增加,土层固结参数值逐渐趋于稳定,最终得出土层体积压缩系数mv为0.201MPa-1,固结系数cv为9.9×10-6m2/s,初始固结时间t0为0.818d,土层渗透系数k为1.99×10-8m/s。
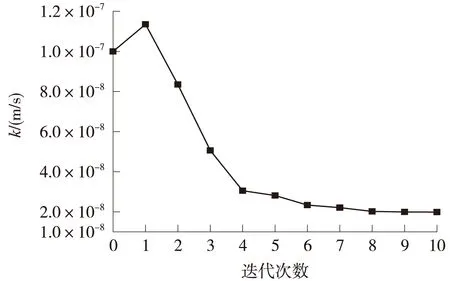
图6 渗透系数k迭代过程
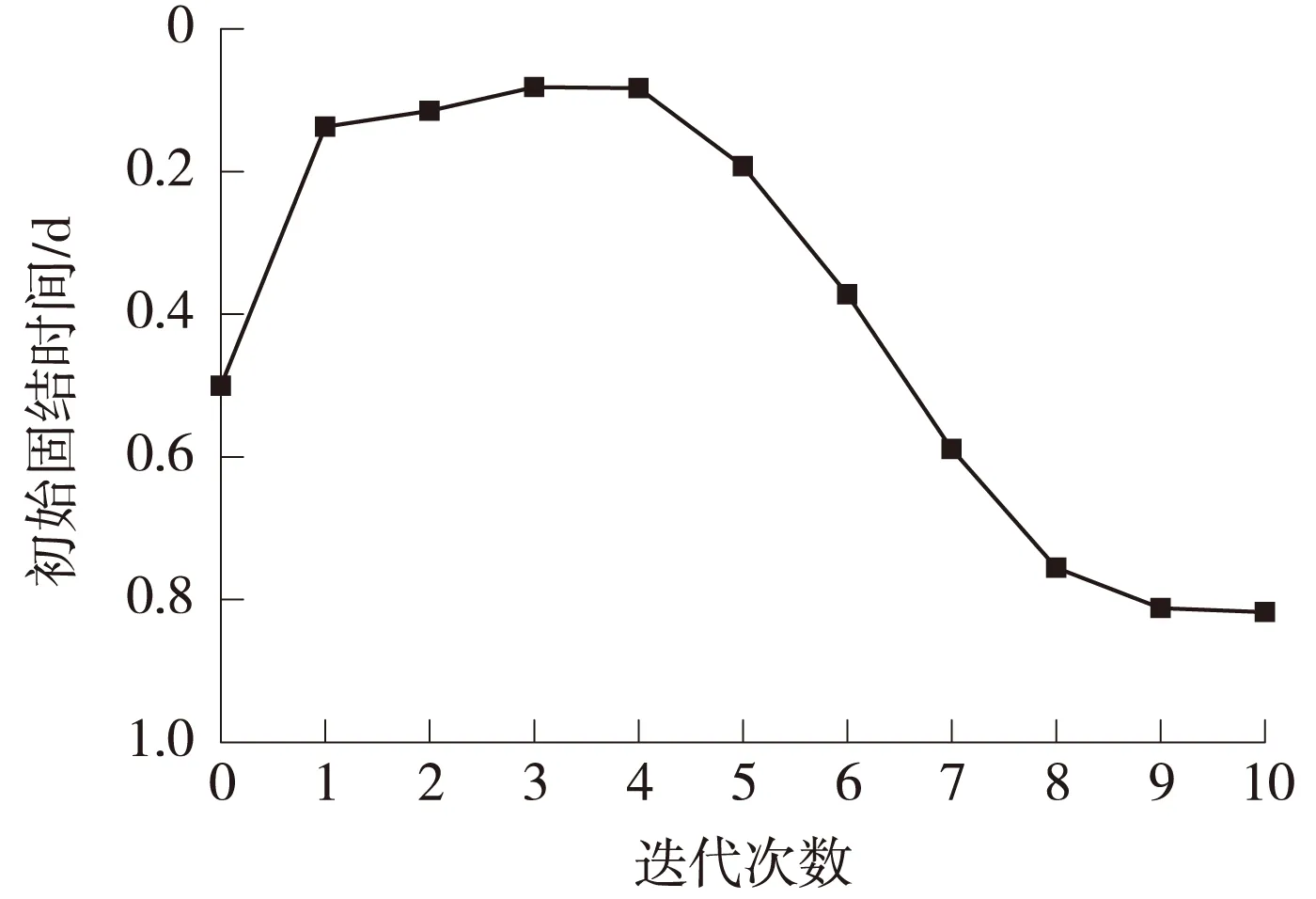
图7 初始固结时间t0迭代过程
分别根据初始估计参数和反分析得出的土层固结参数对土层沉降变化曲线进行预测,与监测结果进行对比,如图8所示。由图8可以看出,由初始估计参数计算的沉降变化曲线与实际监测值差别很大,而跟据反分析参数计算的沉降变化曲线与监测值十分接近,说明反分析得出的土层固结参数是符合实际的,可以进一步用于预测以后的土层沉降变化状况。
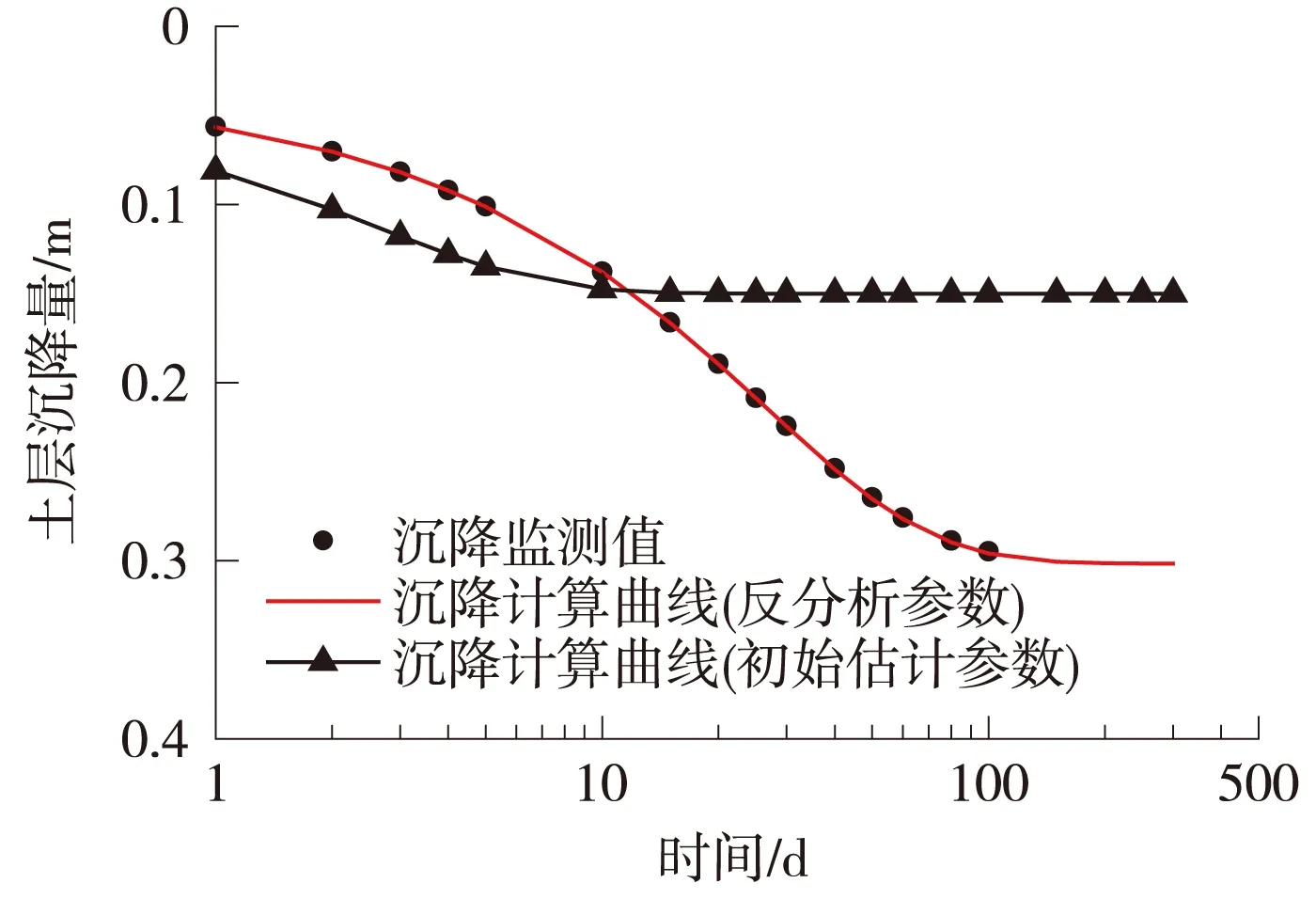
图8 土层沉降变形计算曲线与监测值对比
4 结论
(1)通过对比大面积加载和地下水位下降引发的土层固结问题解析解,得出形式一致可考虑初始固结时间的土层沉降解析表达式。
(2)利用土层沉降变形监测值,建立能综合反映各时间点下沉降监测权重的目标函数,结合土层固结解析解,利用修正Newton-Raphson方法建立固结参数反分析优化求解流程。
(3)针对具体算例对土层的固结参数进行反分析,经过10次迭代得出了符合精度要求的一组固结参数,说明反分析算法的有效性,利用该组参数值计算的土层沉降量与监测值十分接近,能够进一步用于预测土层以后的沉降变化状况。
[1]《工程地质手册》编委会.工程地质手册:第四版[M].北京:中国建筑工业出版社,2007:132-162
[2]中华人民共和国建设部.GB50021—2001岩土工程勘察规范[S].北京:中国建筑工业出版社,2009:117-119
[3]邓永锋,刘松玉,季署月.取样扰动对固结系数的影响研究[J].岩土力学,2007,28(12):2687-2690
[4]李晓萍.土工试验中常见问题探讨[J].铁道勘察,2015,41(1):78-80
[5]郗宁.三轴试件抽气饱和方法及其对固结不排水剪强度试验的影响分析[J].铁道勘察,2013,39(4):39-42
[6]杨志法.岩土工程反分析的发展与展望[C]∥全国岩土工程反分析学术研讨会论文集.台州:中国岩石力学与工程学会,2006:1-11
[7]王绪锋,解廷伟,陈炯钊,等.土体固结参数的反分析与工程应用[J].水运工程,2014(4):154-157
[8]胡荣华,余海忠,张明,等.确定软土固结系数方法的研究[J].铁道建筑,2010(2):74-81
[9]包太,刘新荣,朱凡,等.固结系数的最小二乘法计算[J].岩土工程学报,2005,27(10):1230-1232
[10]邓永锋,刘松玉,洪振舜.基于沉降资料反演固结系数的方法研究[J].岩土力学,2005,26(11):1807-1809
[11]江刚.遗传算法在固结系数计算中的应用[J].重庆建筑大学学报,2006,28(1):50-52
[12]陈仲颐,周景星,王洪瑾.土力学[M].北京:清华大学出版社,1994:143-155
[13]骆冠勇,潘泓,曹洪,等.承压水减压引起的沉降分析[J].岩土力学,2004,25(增):196-200
[14]陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005:287-315
Back Analysis of the Consolidation Parameters of Soil Layer Based on Analytical Solution and Modified Newton-Raphson Method
HUANG Dazhong
2016-03-24
黄大中(1987—),男,2014年毕业于浙江大学岩土工程专业,工程师。
1672-7479(2016)04-0034-03
TU413
A
