垂尾抖振控制中多重动力吸振器设计

牛文超，李　斌

垂尾抖振控制中多重动力吸振器设计

牛文超，李斌

（西北工业大学 飞行器结构力学与强度技术国防重点学科实验室，西安 710072）

针对飞机垂尾抖振抑制的需要，进行小型电涡流耗能动力吸振器设计，并推导多重动力吸振器最优参数设计方法。分别以悬臂梁系统和缩比垂尾为被控对象，并考虑动力吸振器与垂尾实际尺寸，选定合理安装位置，通过有限元仿真验证多重动力吸振器吸振性能，仿真结果表明多重动力吸振器具有良好的振动抑制效果，可满足设计预期要求。

振动与波；抖振抑制；电涡流阻尼力；多重动力吸振器；有限元；优化设计参数

当飞机进行高机动性飞行时，垂尾时常处于不稳定涡流中并产生抖振现象，激起结构的弯扭模态振动，使飞机结构出现振动疲劳问题。动力吸振器是结构振动控制最常见的手段之一，它一般分为主动型、被动型、半主动型、混合型四种形式。主动可调型动力吸振器系统复杂，受成本高、可靠性差、适航性等制约，目前应用范围有限。而被动式动力吸振器作为最常见的形式具有原理和结构简单、可靠性和稳定性高、不需要外界提供能量等特点，在实践中得到广泛的应用。

动力吸振器最早可追溯到1940年，在主结构上连接一个中等质量的振子后，主结构在共振频率附近的共振峰值明显降低。Clark最早研究应用多重动力吸振器在较宽的频带内控制结构振动，并且每个吸振器都在不同的频率上起作用［1］。此后，研究者陆续关注多重动力吸振器在单自由度主结构中的应用，并验证了多重动力吸振器的有效性［1］。目前多重动力吸振器在土木建筑或大型机械结构的应用研究较多，在航空结构的应用研究则较少。

飞机设计对重量限制非常严格，另外飞机垂尾内部空间极为有限，因此用于飞机垂尾抖振抑制的动力吸振器必须满足小型化和轻量化的设计要求。电涡流耗能动力吸振器具有良好的可设计性，阻尼、刚度、质量可以方便地灵活调节，为实现动力吸振器的小型化和轻量化设计提供了一个有效的手段。本文将在前期所研制小型化电涡流耗能动力吸振器的基础上，进一步研究多重小型电涡流耗能动力吸振器在垂尾抖振抑制中的可行性。

1　电涡流耗能动力吸振器简介

本文提出的电涡流耗能动力吸振器空间布局紧凑、基于非接触式电涡流耗能机理、阻尼可设计，并实现刚度和阻尼的完全分离，如图1所示。采用磁铁在铜管内运动的布局形式，通过导体切割磁感线，在导体内部产生电涡流，形成电涡流阻尼。实际尺寸为长90 mm左右，外径45 mm左右，吸振器运动质量可在350 g～600 g之间调节，该电涡流吸振器的阻尼调节范围为2 Ns/m～20 Ns/m。

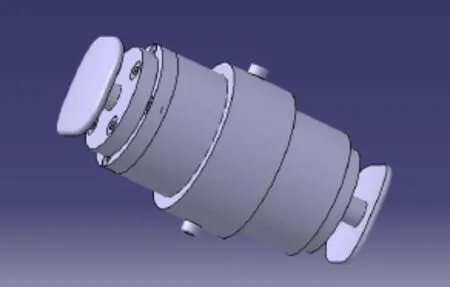
图1　电涡流耗能动力吸振器

2　多重动力吸振器设计方法

对于超过二重的多重动力吸振器很难应用定点理论，需要探索新的方法来进行最优调整［4］。如图2所示，在由质量M与刚度K构成的主振系统上，施加外激励f，并且在其上设置有n个动力吸振器，吸振器质量、刚度、阻尼分别为mi、ki、ci（i=1，2，…，n）。则力学模型的运动方程为

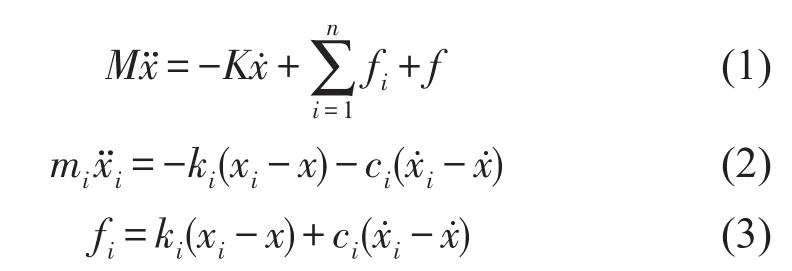
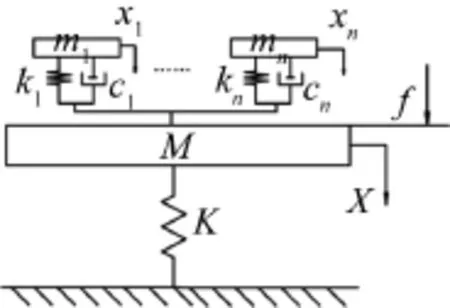
图2　多重动力吸振器的力学模型

在此定义

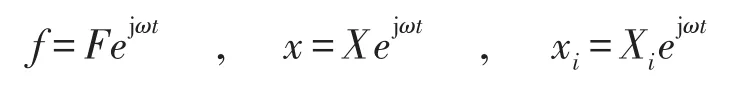
主振系统上的外激励力F与K的比值F/K定义为静变形Xst，并引入以下无量纲参数。

利用以上定义，位移振幅比可表示为

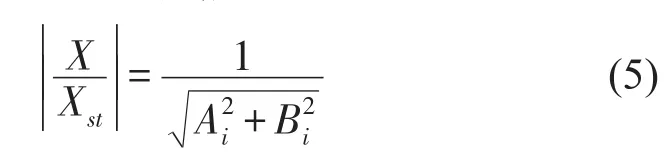
其中

n重动力吸振器主振动系统的位移振幅曲线上存在n+1个极值点。根据这些极值峰定义以下两个评价函数

式中k为峰值个数，J为峰值的最大值。本文采用遗传算法调节多重动力吸振器的最优参数γi（最优同调）、ζi（最优阻尼）使得上述评价函数为最小值。

3　等效悬臂梁的吸振设计分析

首先，以一个与飞机垂尾动力学模型等效的悬臂梁结构为对象，进行多重动力吸振器的性能研究。该等效悬臂梁模型的当量刚度、质量及阻尼取自文献［7］提供的F18飞机的参考数据，一弯等效质量、刚度、阻尼系数和固有频率分别为

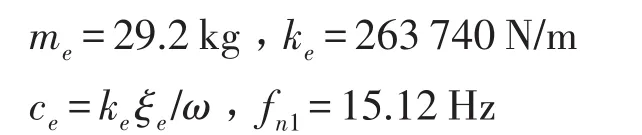
实际设计的等效悬臂梁模型如图3所示，悬臂端长为901.4 mm、宽为137.6 mm、厚为30 mm，端部配重质量为22.315 kg，材料为45号钢。通过模态分析得到该悬臂梁系统的1阶弯曲固有频率为15.201 Hz，与垂尾模型1阶弯曲固有频率的误差为0.54%，由此可见该悬臂梁系统的刚度和质量可以较好地模拟垂尾的1阶振动。

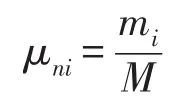
图3　等效悬臂梁模型

四重吸振器的优化设计参数

十重吸振器的优化设计参数

针对设计结果，进行有限元仿真，并与单重动力吸振器的吸振效果进行对比，如图4所示。由图可以看出，具有最优参数设计的多重动力吸振器吸振效果明显增强，吸振器作用频带宽度增加，重数越高吸振器效果越好，并不断趋近于一个最优值。另外需要指出的是，多重吸振器如果简单地处理为多个质量、刚度和阻尼相等的小吸振器，其效果与单一大吸振器的效果是相同的。因此进行多重吸振器的优化设计是非常必要的。对本例，与单一大动力吸振器方案的最大位移振幅比相比，四重动力吸振器共振峰减少16%，十重动力吸振器减少20%。

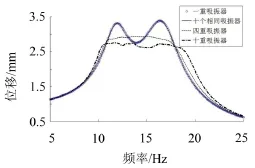
图4　多重动力吸振器吸振效果对比

4　垂尾吸振设计分析

为进一步分析多重动力吸振器对垂尾的吸振效果，以某战机的缩比垂尾模型为对象进行动力吸振器优化设计分析，垂尾模型如图5所示。参照垂尾内部安装空间尺寸与动力吸振器的实际尺寸，选定图5所示的吸振器安装点为参考点，可推导出对应1阶弯曲振型的垂尾等效模型的模态质量、模态刚度分别如表1所示。

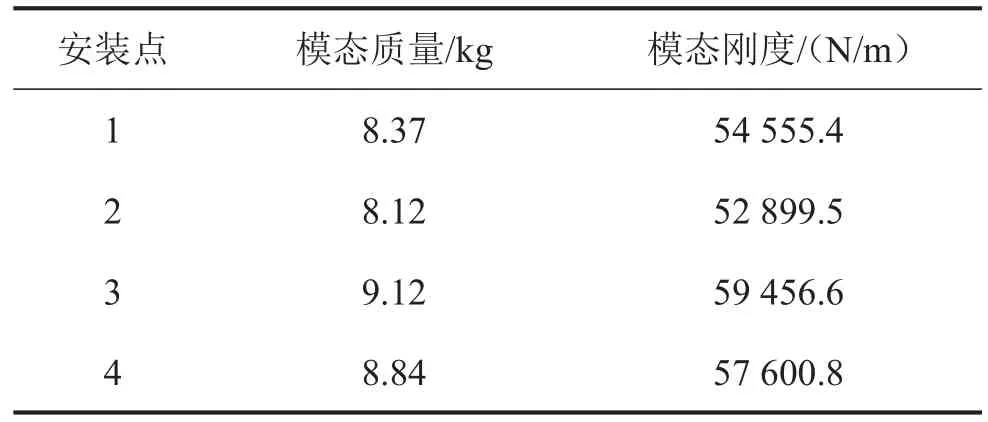
表1　垂尾等效单自由度动力学模型参数

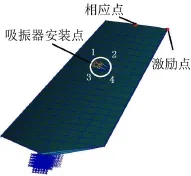
图5　垂尾模型

进一步确定动力吸振器参数，选取3号点为单一动力吸振器安装点，通过有限元分析可以得到垂尾最大位移响应与动力吸振器质量的关系，结果如图6所示。可以发现，垂尾的最大位移响应随动力吸振器质量增加而减少，且曲线斜率逐渐降低。当动力吸振器质量大于1.7 kg时，曲线斜率变为最小且保持不变。考虑到轻型化的设计要求，选定动力吸振器质量为1.7 kg。

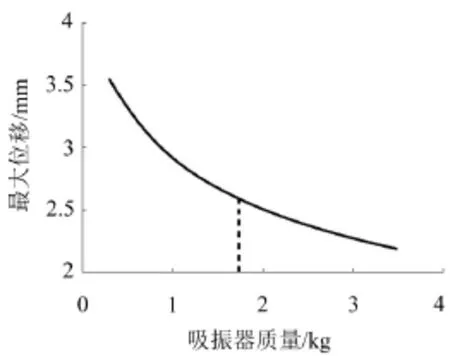
图6　垂尾最大位移响应与吸振器配重的关系

分别对垂尾安装单一动力吸振器、未安装动力吸振器和安装四个动力吸振器等工况进行了有限元仿真分析。计算过程中激励点的响应拾取点如图5所示，激励为单位激励。首先，对比未安装动力吸振器与安装单一动力吸振器两种工况下的垂尾端部的位移频率响曲线，结果如图7所示。未安装动力吸振器垂尾端部的最大位移为2.44 mm，安装单一动力吸振器的最大位移为0.197 mm，垂尾的最大减幅比为92%。

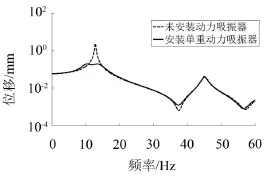
图7　单位激励激起的频率响应

下面进一步研究多重动力吸振器的吸振性能，上节中限定了吸振器的总质量元素为1.7 kg。参照电涡流动力吸振器的实际参数，本文采用四个动力吸振器进行分析，每个吸振器质量为0.425 kg。将四个动力吸振器分为三种不同的工况：

（1）以其中一点为参考点确定动力吸振器刚度阻尼参数，四个动力吸振器参数完全相同。

（2）四点分别作为参考点确定各自的动力吸振器参数。

（3）以其中一点为参考点，采用上节方法得到的多重动力吸振器的最优设计参数矩阵，确定吸振器刚度、阻尼参数。

对比上述三种工况下的垂尾端部的位移频率响应曲线，结果如图8所示。工况一的最大位移响应为0.334 mm、工况二的最大位移响应为0.285 mm、工况三的最大位移响应为0.165 mm。工况三的最大减幅比为93.24%。由此可见，若满足多重动力吸振器的最优设计参数时，吸振器的吸振效果明显增强，吸振频带增宽。

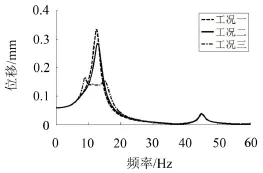
图8　多重方案的频率响应对比

如图9进一步给出了单一大动力吸振器与最优四重动力吸振器之间的结果对比，四重动力吸振器的响应峰值比单重方案降低16.2%，与等效悬臂梁算例效果相当。

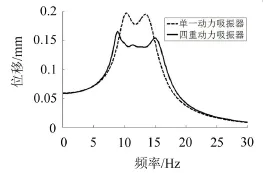
图9　单重与四重方案的对比

5　结语

针对垂尾抖振抑制的需要，提出利用电涡流耗能动力吸振的设计参数可分离设计，及便于小型化等特点，开展了多重动力吸振的优化设计方法研究。

分别以等效悬臂梁模型和垂尾模型为例，参照所设计的电涡流耗能动力吸振器的具体参数，通过有限元仿真分析验证了多重动力吸振器在等效悬臂梁模型和垂尾模型中的吸振效果。分析结果表明，符合最优参数设计的多重动力吸振器的吸振效果明显，并且吸振效果要高于单一大吸振器方案。相关研究结果可为进一步的工程实用设计提供有益参考。

［1］HOUSNER G W，BERGMAN LA，CAUGHEY T K，et al. Structural control：past，present，and future［J］.ASCE Journal of Engineering Mechanics，1997（123）：897-971.

［2］JANGID R S.Dynamic characteristics of structures with multiple tuned mass dampers［J］.Structural Engineering and Mechanics，1995（3）：497-509.

［3］JANGID R S，DATTA T K.Performance of multiple tuned massdampersfortorsionallycoupledsystem［J］. Earthquake Engineering and Structural Dynamics，1997（26）：307-17.

［4］张炳康，何立东，杨秀峰.颗粒碰撞环形调谐质量阻尼器的设计与实验［J］.噪声与振动控制，2014，34（4）：142-147.

［5］李斌，牛文超，徐兆懿.电涡流耗能动力吸振器设计与试验研究［J］.西北工业大学学报，2016，34（1）：18-24.

［6］背户一登.动力吸振器及其应用［M］.北京：机械工程出版社，2013：1-2.

［7］JOSEPHRMALY，KEVINL.NAPOLITANO.A magnetic tuned mass damper for buffet-induced airfoil vibration［EB］//http www.csaengineering.com，2010.

Design of Multiple Dynamic VibrationAbsorbers for Buffet Control of Vertical Tails

NIU Wen-chao，LIBin
（Fundamental Science onAircraft Structural Mechanics and Strength Laboratory，Northwestern Polytechnical University，Xi'an 710072，China）

Aiming at the need of vertical tail buffet suppression，the eddy current vibration absorber is designed and its parameters is introduced.The optimal design parameters method of the multiple dynamic vibration absorber is deduced to realize the vibration absorber miniaturization.Taking an equivalent cantilever beam system and a scaled vertical tail as the objects respectively for vibration control，considering the actual size of the vibration absorber and the vertical tail，and choosing the reasonable installation position，the vibration absorption effect of the multiple-dynamic-vibration-absorber is verified through the finite element simulation.Simulation results show that the vibration suppression property of the multiple-dynamic-vibration-absorber scheme is very good.Compared to the single large dynamic vibration absorber，the vibration attenuation rate of the quadruple dynamic vibration absorber scheme is increased by 16%，and will be raised by 20%for the ten-dynamic-vibration-absorber scheme.

vibration and wave；buffet suppression；eddy current damping force；multiple dynamic vibration absorber；finite element；optimal design parameters

V214

ADOI编码：10.3969/j.issn.1006-1335.2016.03.040

1006-1355（2016）03-0197-04

2015-10-20

国家自然科学基金资助项目（11172238）；中央高校基本科研业务费专项资金资助项目（3102014KYJD015）

李斌（1975-），男，湖北咸宁人，教授，博士生导师，主要研究方向为结构动力学与控制。E-mail：leebin@nwpu.edu.cn