土质边坡地震动力响应规律研究1
2016-10-14张江伟高晓莉李小军王世文王玉石
张江伟 高晓莉 李小军 王世文 王玉石
土质边坡地震动力响应规律研究1
张江伟1)高晓莉2)李小军3)王世文1)王玉石3)
1)河北地质大学,勘查技术与工程学院,石家庄 050031 2)山东外国语职业学院,信息工程学院,日照 276826 3)中国地震局地球物理研究所,北京100081
地震往往会触发大量的山体滑坡,给人类和社会带来巨大灾难。为研究探索土质边坡在地震作用下的动力响应规律,本文建立了二维均质边坡有限元模型,模拟计算了其在地震作用下的动力响应,对地震响应中学术界和工程界最为关心的加速度、位移和频谱特性响应进行了研究分析,并得到以下几点结论:①在坡顶和坡面处,与输入地震动加速度时程比较,输出加速度峰值出现的时刻有滞后现象;②坡体内部对输入地震动PGA存在垂直和临空面放大作用,同时垂直放大作用呈现出节律性变化的特点;③地震作用下坡体的最大变形在水平方向上出现在坡脚处,在竖直方向上出现在坡肩处;④边坡体内部对输入地震动的频谱成份产生滤波作用,滤掉了输入地震动中的高频成份,且随着高度的增加,这种滤波作用呈现增强的趋势。
地震 土质边坡 动力响应 模拟分析
引言
地震是触发滑坡灾害发生的重要因素之一,例如2008年05月12日发生在我国四川省汶川县的S8.0级大地震引发了多达35000处滑坡,据不完全统计,地震引发的次生地质灾害造成的人员死亡约占地震总死亡人数的1/3,其中致100人以上死亡的重大灾难性滑坡就达20余处(黄润秋,2009),给当地人们的生命财产安全造成了严重的损害。因此地震作用下边坡的动力稳定性问题一直是受国内外专家普遍关注和研究的一个课题,尤其在2008年汶川地震诱发了大量的滑坡灾害以后,边坡动力稳定性研究再一次引起了国内外学者的高度重视。
目前边坡地震动力分析方法有很多,如拟静力法、Newmark滑块分析法、模型试验法、数值模拟分析法等。其中数值模拟方法能够较好地考虑地震动的特性及复杂边坡岩土体的动力特性,反映地震过程中边坡安全系数随时间的动态变化过程,自动求解得到边坡滑移面。因此,数值模拟分析法在近年来被广泛地运用到边坡地震响应分析中。Lee(1974)和Serff(1976)早期提出了利用有限元法计算永久边坡位移的一种方法,即在计算应变趋势时对坡体的刚度进行了折减,地震作用下的边坡位移是利用初始剪切模量和折减的剪切模量两种静力有限元分析所得到的节点位移差。徐光兴等(2008)利用FLAC3D软件分析研究了地震动参数对土质边坡动力响应的影响规律。李果等(2011)针对2008年汶川地震诱发的典型反倾软弱基座的灌滩滑坡,建立了有无软弱基座两种结构斜坡的概化模型,揭示了斜坡在地震动力响应过程中的应力演化过程及其破裂的产生和延展趋势。言志信等(2011)通过FLAC3D软件对顺层岩质边坡的地震动力响应进行数值模拟,认为岩体材料的滤波作用与土体材料相比并不明显,仅仅是对某一频率的地震波存在显著的放大作用。李鹏等(2013)运用UDEC离散元软件研究了软弱层的特性对岩质边坡动力响应的影响,为动力荷载作用下边坡防灾减灾提供了指导依据。杨果林等(2015)以大理至瑞丽铁路沿线边坡支挡结构为研究对象,对基覆边坡的3种不同支挡结构在地震荷载下的动力特性进行数值模拟研究。白广斌等(2014)针对某核电取水隧洞工程,采用FLAC3D模拟分析了隧洞洞口处回填高边坡在地震作用下的响应规律,并进行了洞口边坡在地震动作用下的稳定性分析。
本文在前人的研究基础上建立二维土质边坡模型,选用实际地震动记录作为输入对边坡模型进行时程分析,充分考虑人工边界问题,并从坡面到坡体内部、沿水平方向与竖直方向等多方位来全面地探索分析土坡体在地震作用下的动力响应规律,从而得到有关结论。
1 动力计算原理
地震动力有限元方法采用如下平衡方程:
对于求解地震作用下的动力问题,动力荷载就是地震荷载,于是求解边坡地震动力稳定性问题的基本力学运动方程可写为:
地震是一种完全随时间变化的复杂荷载,边坡岩土体在地震作用下往往会进入弹塑性状态,这时便无法得到解析解,解析方法也不再适用,但通过数值计算可以得到结构动力反应的数值解。常用的方法有分段解析法、中心差分法、平均常加速度法、线性加速度法、Newmark-法和Wilson-法,这些方法的中心思想是假定结构在每一个微小时间步内呈现线弹性反应,然后通过在时域内逐步积分求解。在ABAQUS中分为隐式和显式两种算法,其中隐式算法是以Newmark-法为基础,而显式模块则采用中心差分法来解决动力学问题。本文中采用隐式算法。
2 模拟计算条件
2.1 本构模型
对于边坡土体材料,本文在模拟分析中选用理想弹塑性本构模型,屈服准则采用摩尔-库仑强度准则。摩尔-库仑强度准则适用于岩石和土体的力学行为,它的破坏包络线主要依据剪切屈服函数和拉应力屈服函数。
2.2 边界条件
在进行半无限空间体的地震动力模拟分析时,需要考虑边界条件的设置。与静力问题中的边界条件不同,由于边界存在对地震波的反射、折射问题,如果不对边界进行处理,势必会影响计算结果的准确性。目前通用的用于解决动力问题的边界条件设置方法主要有简单截断边界、粘弹性边界和透射边界,这些方法各有利弊。本文采用适合用于模拟边坡地震稳定性的粘弹性边界,其中二维粘弹性人工边界等效物理系统的弹簧系数和阻尼系数分别由下式求得:
(4)
(6)
(7)
2.3 边坡模型建立
为研究边坡在地震作用下的动力响应特性,建立如图1所示的概化边坡模型。模型参考徐光兴等(2008)的论文,并在其基础上,将模型尺寸扩大,以便进一步消除边界的影响。有限元模型如图1所示,长×高=170m×70m,边坡坡角为34°,坡高30m,边坡坡顶后缘长为80m。在模拟分析边坡等半无限体的动力问题时,为了防止地震波传播到模型边界处反射回模型,通常需要设置人工边界,允许必要的能量发散。因此本模型底部采用静态边界条件,侧面设置粘弹性边界。本构模型为理想弹塑性本构模型,采用摩尔-库仑强度准则作为屈服准则。边坡土体的力学参数见表1。为充分研究分析边坡在地震作用下的响应规律,模型材料设置为均质材料。

表1 边坡土体参数
阻尼的设置是模拟计算中关键的一个环节,工程中常常采用Rayleigh阻尼,即通过质量矩阵和刚度矩阵的线性组合来表述:,其中为质量阻尼系数,为刚度阻尼系数。当计算选用的两阶阻尼比与结构阻尼比相等时,和可由下式确定:
(9)
2.4 输入地震动
地震动输入选用实际地震动记录加速度时程,截取“Loma Prieta,10/18/1989,UCSC,90°”记录中时长19.98s的一段加速度时程,将幅值设置为1m/s2,输入到模型底部的水平方向上。图2和图3分别为地震动加速度时程曲线以及傅里叶谱。
3 模拟计算效果验证
成功合理地施加地震荷载以及人工边界是保证计算模拟正确性的前提。为了更全面地验证地震荷载和人工边界施加的效果,在程序完成计算后,提取图1中模型底部观测点A、B、C的加速度时程并做对比分析,如图4所示。由图4结果可知,输出与输入的加速度时程曲线吻合程度较高,从而较好地验证了地震动时程输入的正确性和人工边界施加的良好效果。本文模拟计算得到结果中,加速度响应与徐光兴等(2008)的结果较为接近,坡面变形位移的差别小于等于一个数量级,在合理范围内,这是由于输入地震动和模型参数的不同所造成的。
4 结果分析
4.1 加速度响应
模型观测点的布置如图5所示。提取观测点H21和V11的加速度时程,时程曲线如图6和图7,发现观测点对输入地震动均有不同的放大的作用,两点输出的加速度峰值分别出现在8.1s和7.6s左右,分别为1.68m/s2和1.59m/s2,与峰值出现在5.8s的输入加速度时程对比,峰值出现的时刻均有滞后现象,而且是随着高度的增加滞后时间越长,在坡顶处到达峰值的时刻比输入延迟了2.3s左右。
为了进一步分析坡体对输入地震动加速度的放大规律,规定坡体内部各点输出加速度时程的最大绝对峰值与输入加速度绝对峰值的比值为边坡PGA动力放大系数。下面分别分析不同高度上坡面各点以及同一高度上坡体内外部的加速度响应规律。
由竖直向各观测点PGA动力放大系数曲线(图8)可知,高程最低的两点V61和V26的PGA动力放大系数最小,分别为0.99和1.06;随着坡体高度增加到V51和V25,PGA动力放大系数也随之增大到1.06和1.13;当高度增加到V41和V24位置时,这两点对PGA的放大系数分别为1.01和1.10,较上两点出现减小现象;之后PGA放大系数则随着高度增加继续增大,在坡顶V11和V21两点处达到最大值,分别为1.65和1.45。总体上看,坡体的PGA放大系数呈现随高度增加先增大后减小又增大的变化规律,由于只有在点V41和V24所处的高度是减小的,所以整体呈现出节律性增长的规律。
为揭示坡体内、外部对输入地震动峰值放大效果的差异,考察坡面点和同一高度上坡体内部共8个观测点的输出加速度对峰值的放大效果,如图9所示。坡面上H11和H21两点对PGA动力放大系数最大,分别是1.41和1.58。在同一高度上,随着观测点的位置向坡体内部延伸,其PGA动力放大系数整体呈现逐渐减小的变化规律。由图可知,处于最内部的H14和H24点的PGA动力放大系数最小,分别为1.21和0.9。可见在同一高度上坡面对输入地震动的放大作用要大于坡体内部,出现了临空面放大作用,究其原因是临空面对地震波的反射叠加作用导致的。
纵观上述规律,印证了王存玉等(1987)通过边坡动力模型试验观测到的加速度垂直向放大效应和徐光兴等(2008)、何蕴龙等(1998)通过数值模拟得到的垂直、临空面放大作用,以及祁生文等(2003)经过模拟得到的PGA动力放大系数随边坡高度呈现出节律性增长的规律。
4.2 变形位移响应
由边坡最终变形位移云图(图10)可知,边坡坡面相对其他部位变形要显著得多。
提取图10中坡面6个观测点的水平向和竖直向变形位移响应时程,如图11、图12所示。
可以发现,随着地震动的持续作用,在刚刚发震时,由于边坡材料尚处于弹性阶段,因此变形在原点附近波动,并没有产生永久位移;随着地震动的持续作用和幅值的增大,坡面各点均发生明显的变形,在6—9s时间段内,位移增加显著,之后便趋于稳定,在地震动作用结束时产生永久变形位移。水平方向上,坡面最大变形发生在P5点,即坡脚处;竖直方向上,坡面最大变形发生在P1点,即坡肩处。
4.3 频谱响应
提取图13中的输入点V和输出点V11和V61三个观测点的输出加速度时程并进行傅里叶变换,得到三个观测点输出加速度响应的傅里叶谱值,如图14、15和16所示。对比输入加速度时程的傅里叶谱,输出的频谱均发生明显变化:输入的傅里叶谱中频率分布范围比较广,直到20Hz以上的频段成份占有才变小;而V61点输出的傅里叶谱中,11Hz以上的频段成份很少,几乎为零。随着高程的增加,位于坡顶处V11点输出的傅里叶谱中的高频成份继续减少,由图16可知,7.5Hz以上的频段成份占比几乎为零。
综合以上现象不难发现,坡体内部对输入地震动的频谱成份产生了滤波作用,滤掉了输入地震动中的高频成份,且随着高度的增加,坡体对高频段的滤波作用增强。
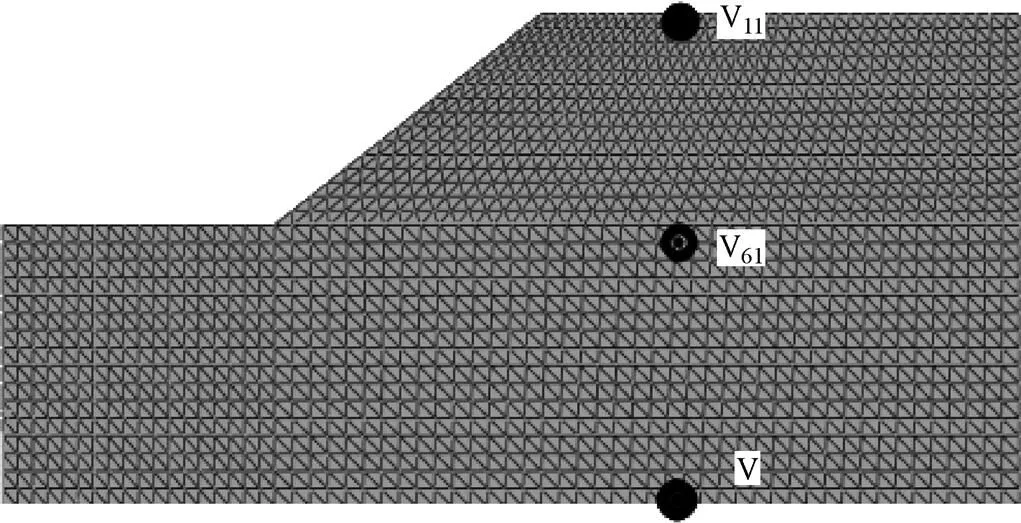
图13 边坡模型观测点位示意图
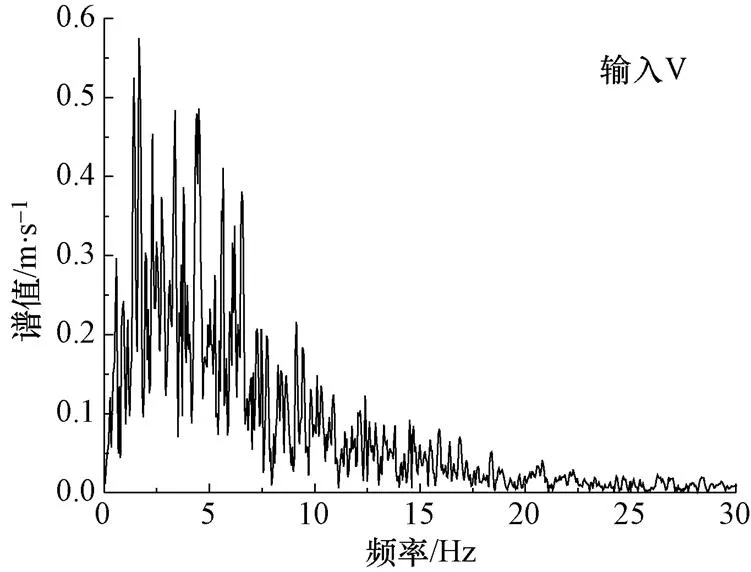
图14 输入地震动傅里叶谱
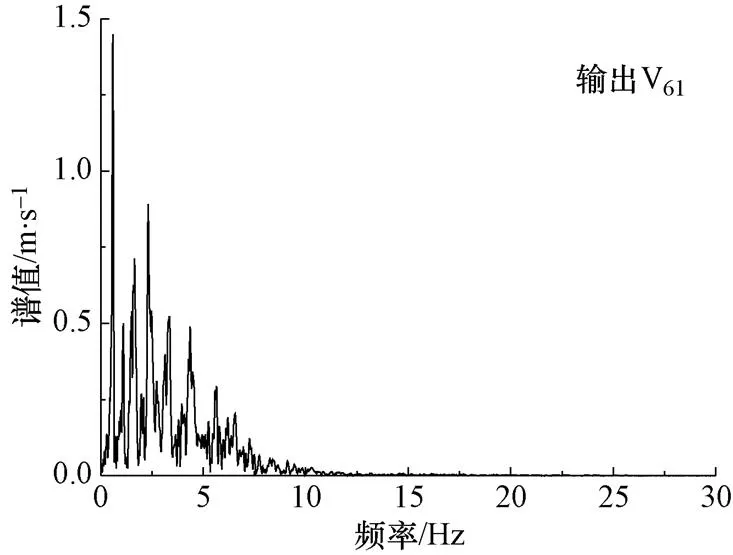
图15 输出点V61的傅里叶谱
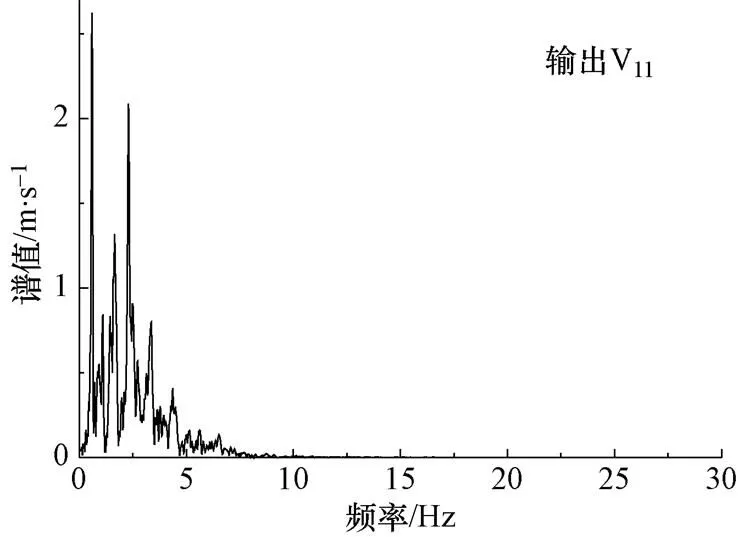
图16 输出点V11的傅里叶谱
5 结论与讨论
本文主要分析研究了边坡的地震动力响应规律。通过建立有限元边坡模型,并进行动力模拟计算,分析边坡加速度、位移和频谱响应的特性,从而得到了以下结论:
(1)在坡顶和坡面处,坡体对输入地震动均有不同程度的放大的作用,而且输出加速度峰值出现的时刻有滞后现象。文中选取的两个观测点输出的加速度峰值分别出现在8.1s和7.6s,与峰值出现在5.8s的输入加速度时程相比,在坡顶处峰值出现时刻比输入延迟了2.3s左右。
(2)坡体内部对输入地震动PGA存在垂直和临空面放大作用。垂直放大作用即是PGA放大系数随着高度的增加而变大,祁生文等(2003)曾指出PGA动力放大系数随高程呈现出节律性变化,在算例中接近边坡脚的位置也出现了这种节律性的变化;临空面放大作用,即是坡体同一高度上坡面对输入地震动的放大作用要大于坡体内部,这是由临空面对地震波的反射叠加作用导致的。
(3)随着地震动的持续作用和幅值的增大,坡面各点在地震动作用结束时产生永久位移。水平方向上,坡体最大变形出现在坡脚处;竖直方向上,坡体最大沉降变形出现在坡肩处。
(4)边坡体内部对输入地震动的频谱成份产生滤波作用,滤掉了输入地震动中的高频成份,且随着高度的增加,这种滤波作用有增强的趋势。
白广斌,赵杰,易剑等,2014.某核电取水隧洞洞口段及洞口高边坡抗震稳定分析.岩土力学,35(z2):488—494.
何蕴龙,陆述远,1998.岩石边坡地震作用近似计算方法.岩土工程学报,20(2):66—68.
黄润秋,2009.汶川8.0级地震触发崩滑灾害机制及其地质力学模式.岩石力学与工程学报,28(6):1239—1249.
李果,黄润秋,巨能攀等,2011.软弱基座型滑坡震裂机理研究.工程地质学报,19(5):712—718.
李鹏,苏生瑞,王闫超等,2011.含软弱层岩质边坡的动力响应研究.岩土力学,34(z1):365—370,378.
刘晶波,谷音,杜义欣,2006.一致粘弹性人工边界及粘弹性边界单元.岩土工程学报,28(9):1070—1075.
祁生文,伍法权,孙进忠,2003.边坡动力响应规律研究.中国科学E辑,33(z1):28—40.
王存玉,王思敬,1987.地震条件下二滩水库岸坡稳定性研究.//岩体工程地质力学问题(七).北京:科学出版社.
徐光兴,姚令侃,李朝红等,2008.边坡地震动力响应规律及地震动参数影响研究.岩土工程学报,30(6):918—923.
言志信,张森,张学东等,2011.顺层岩质边坡地震动力响应及地震动参数影响研究.岩石力学与工程学报,30(S2):3522—3528.
杨果林,申权,杨啸等,2015.基覆边坡支挡结构的加速度放大系数数值与试验研究.岩石力学与工程学报,(2):374—381.
Lee K. L., 1974. Seismic permanent deformations in earth dams. Los Angeles: School of Engineering and Applied Science, University of California, Report No. UCLA-ENG-7497.
Serff N., Seed H. B., Makdisi F. I., Chang C. K., 1976. Earthquake induced deformations of earth dams. California: Earthquake Engineering Research Center, University of California, Berkely, Report No. EERC/76-4.
Dynamic Response Analysis of Soil Slope under Seismic Wave
Zhang Jiangwei1), Gao Xiaoli2), Li Xiaojun3), Wang Shiwen1)and Wang Yushi3)
1) College of Prospecting Technology and Engineering, Hebei GEO University, Shijiazhuang 050031, China 2) Institute of Information Engineering,Shandong Foreign Languages Vocational College, Rizhao 276826, China 3) Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
Earthquakes often trigger a large number of landslides, which bring huge disaster to human and society. To explore the dynamic response rules of soil slope under seismic wave, we establish a two-dimensional finite element model of homogeneous slope, and simulates the dynamic response of the slope under seismic. Then we analyze the slope seismic response of the acceleration, displacement and spectrum characteristic which are mostly concerned about by the academic and engineering fields. Our conclusions of the study include: (1) In comparison with the input earthquake waves, the time of output acceleration peak in the top and surface of the slope presents hysteresis phenomenon. (2) The PGA amplification effect of the input seismic waves is existed in the slope’s free face, also along the vertical, which presents a rhythmic vertical amplification change. (3) After the seismic action, the maximum horizontal displacement of the slope are located in slope foot, and the maximum vertical displacement of the slope appeared at slope shoulder. (4) The slope has filtering effects on the high frequency spectrum component of the input earthquake waves. With the increase of height, such effect has the trend of aggrandizement.
Seismic; Soil slope; Dynamic response; Simulation analysis
10.11899/zzfy20160407
国家自然科学基金(51578514,51639006);博士科研启动项目(BQ201616)
2016-06-30
张江伟,男,生于1988年。博士,讲师。从事岩土地震工程研究。E-mail:zjwok1988@sina.com
