3次谐波电流注入对五相感应电机系统运行性能影响分析

朱 鹏 乔鸣忠 张晓锋 易 俊 魏永清



3次谐波电流注入对五相感应电机系统运行性能影响分析

朱 鹏1乔鸣忠1张晓锋1易 俊2魏永清1

（1. 海军工程大学电气工程学院 武汉 430033;2. 重庆邮电大学光电工程学院 重庆 400065）

五相感应电机系统采用集中整距绕组结构并由非正弦供电，可以通过注入谐波改善电机的气隙磁场，从而提高电机的输出功率。本文在3次谐波注入控制策略研究基础上，从母线电压利用率、系统功率因数、效率及输出转矩等性能指标出发，深入研究了3次谐波注入对系统的运行性能影响。最后，搭建了系统实验平台，对实验室一台5.5kW五相集中整距绕组感应电机进行了相关实验。结果表明，在五相集中整距绕组感应电机系统中，通过注入按照一定规律变化的3次谐波，可以有效改善电机系统的运行性能。

气隙磁通密度 电压利用率 功率因数 效率 转矩密度

0 引言

为了在低电压等级下实现高功率的交流传动系统，并提高系统可靠性，多相电机变频调速系统作为有效的解决方案之一应运而生。当前，对于多相系统的研究和应用已达到了前所未有的高度[1-4]。

国外学者于20世纪60年代开始，已涉足多相感应电机的研究，并逐渐成为研究的热点，取得了丰硕的成果，代表学者有H. A. Toliyat、T. A. Lipo及Y. F. Zhao等[5,6]；国内学者近年来对多相电机系统的研究作了大量工作，也取得了一定原创性成果[7-11]，主要体现在电机设计及参数计算、电磁场分析和电机控制等方面。

多相电机系统采用集中整距绕组结构并由非正弦供电，通过改善电机的气隙磁场，可提高电机的输出功率。已有研究表明，当气隙磁通密度基波与3次谐波分量幅值之比为6∶1，相位关系为“峰谷”相对时，其合成的波形最接近理想的方波。此时，对于电机铁心的利用较为充分，功率密度相对较高[8]。

在此研究结论基础上，一些文献对3次谐波注入的多相电机控制策略进行了研究[12,13]。文献[14]更是从系统稳定性的角度，采用分支法分析了3次谐波注入对于多相电机系统的影响，研究表明，通过注入按一定规律变化的3次谐波电流可以有效地提高系统的稳定性。但是，这些对于3次谐波注入可改善多相系统运行性能的论证尚不够，还有待更深入的研究。

文献[15]从电机气隙磁通密度为准方波的控制目标出发，研究了3次谐波电流注入的五相感应电机控制方法。本文将在此研究的基础上，从母线电压利用率、电机的电磁转矩、效率及功率因数等方面出发，深入分析3次谐波注入对五相感应电机运行性能的影响，进一步验证在五相感应电机系统中，3次谐波注入方法的可行性和有效性。

1 电流有效计算

分析3次谐波电流注入对系统的影响时，涉及到各轴稳态电流分量的计算，而这些量与电磁转矩密切相关。为此，首先要解决电磁转矩计算问题。

为了保证气隙磁通密度始终为准方波，必须注入按照一定规律变化的3次谐波电流。此时，电磁转矩表达式将相当复杂，为了后续相关问题分析方便，必须予以简化计算。

考虑3次谐波注入时，五相感应电机的输出电磁转矩可表示为

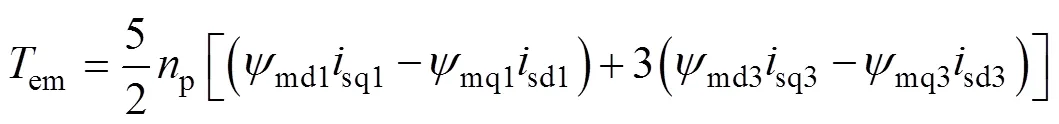
式中，p为电机极对数；md1、mq1分别为基波气隙磁链直轴、交轴分量；md3、mq3分别为3次谐波气隙磁链直轴、交轴分量；sd1、sq1分别为基波电流直轴、交轴分量；sd3、sq3分别为3次谐波电流直轴、交轴分量。

将气隙磁链各轴分量、基波电流与3次谐波电流各轴分量之间的关系代入式（1），电磁转矩表达式进一步表示为

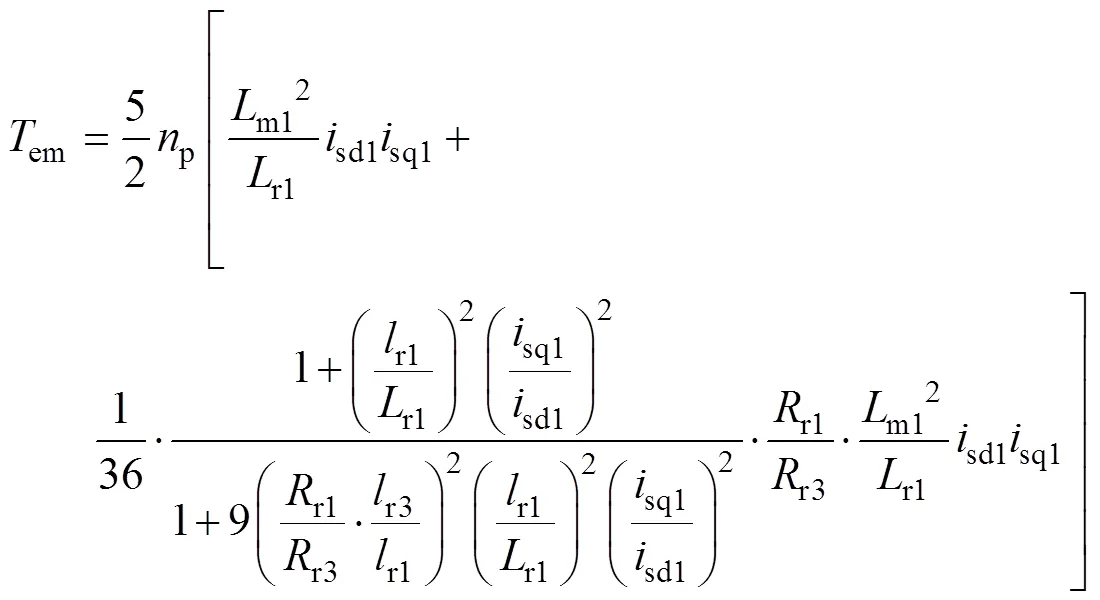
由于转子基波漏感相对转子基波自感来说很小（对于本文中的五相感应电机来说，），则电磁转矩表达式可简化为

由式（3），考虑3次谐波注入时，五相感应电机电磁转矩修正系数

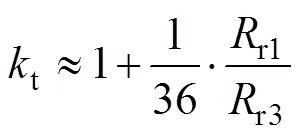
不考虑机械摩擦时，负载转矩等于电磁转矩，基波直轴电流分量sd1保持恒定，根据式（3），就可以很容易计算出sq1，进一步根据基波、3次谐波电流各轴分量之间的关系，可以求出sd3、sq3。

2 3次谐波电流注入对五相感应电机系统性能的影响

本节将在前面定子电流各轴分量计算的基础上，从母线电压利用率、功率因数、效率、转矩等性能指标出发，分析3次谐波电流注入对系统的 影响。

2.1 母线电压利用率变化

母线电压利用率是衡量变频器系统性能的一个重要指标。提高其利用率的意义在于，在相同的直流母线电压下，逆变器输出（基波）电压幅值大，意味着可驱动电压较高的电机负载。

将基波电流与3次谐波电流各轴分量之间的关系代入电机的定子电压方程，定子电压表达式可进一步表示为

其中

式中，sd1、sq1分别为基波电压直轴、交轴分量；sd3、sq3分别为3次谐波电压直轴、交轴分量；m1、m1分别为基波气隙磁链幅值和相位；s为定子绕组电阻，s1、s3分别为定子基波、3次谐波漏感；m3为定转子3次谐波互感；s1为基波空间转差角速度；e1为同步旋转角速度；r为转子旋转角速度。

由式（4），相电压基波分量、3次谐波分量有效值和初始相位可以表示为

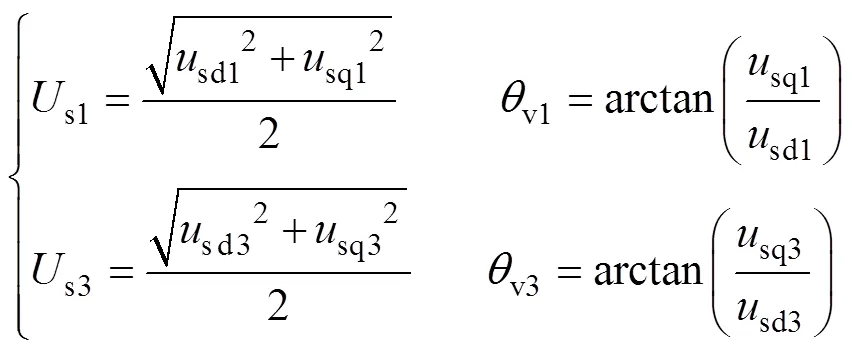
图1为v、Dqv随负载转矩不断变化过程中的曲线。从图1中可以看出，3次谐波与基波幅值比随负载的增加而增大，而两者初始相位差随负载的增加而减小，造成相电压波形中的两个“波峰”电压差值增大。这主要是由于3次谐波漏感压降随负载增大相对较快引起的。

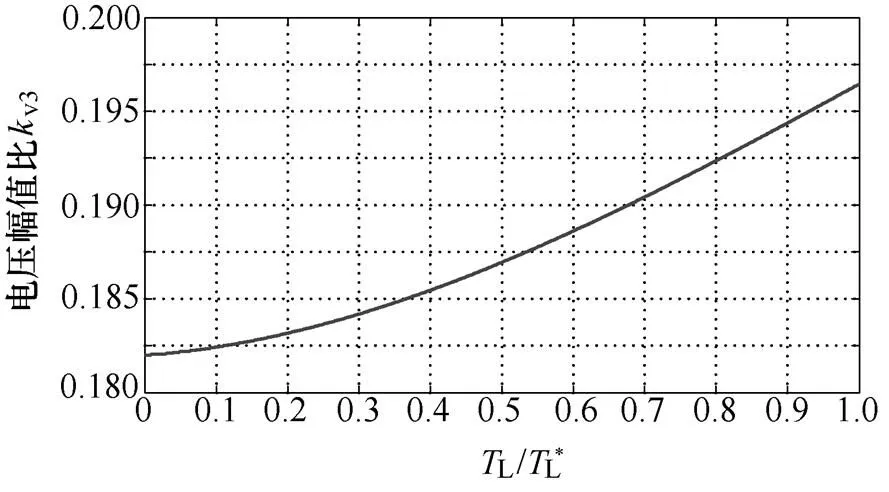
（a）kv随负载变化曲线

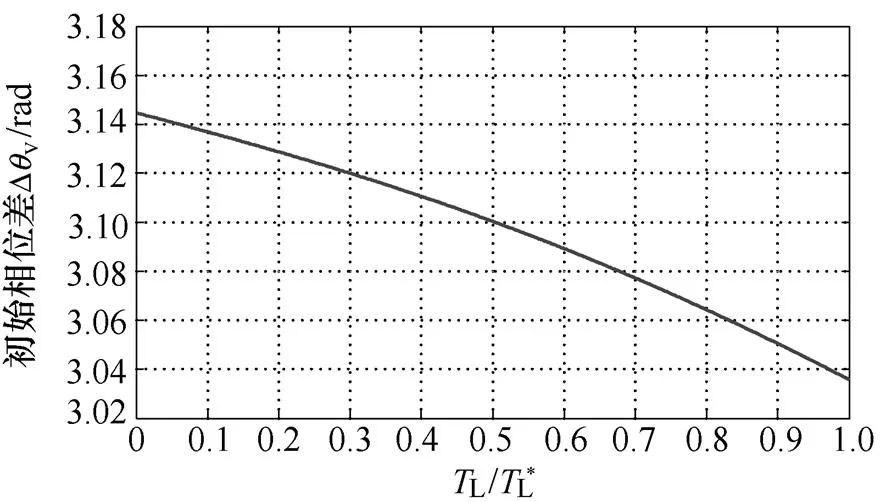
（b）v随负载变化曲线

图1 3次谐波、基波电压幅值比及初始相位差分别随负载变化的关系曲线

Fig.1 Relational curves of the magnitude ratio and initial phase difference between third harmonic and fundamental voltage with varied load

电机空载、注入3次谐波电流情形下，相电压3次谐波与基波分量相位关系为“峰谷”相对，此时电压利用率最大，与只含有基波作用（未注入3次谐波电流）相比，直流电压利用率提高了15.2%（理想情况下）。随着负载的增大，相电压3次谐波与基波之间初始相位差逐渐减小，造成相电压波形在半个周期内的对称性畸变，从而使得电压利用率提高与电机空载时相比减小了。与只含有基波电流作用相比，额定工况下，电压利用率依然提高了12.3%（理想情况下）。

2.2 电机功率因数变化

下面将通过对比不同情形（注入、未注入3次谐波），分析3次谐波电流注入对电机功率因素的影响。

（1）基波功率因数

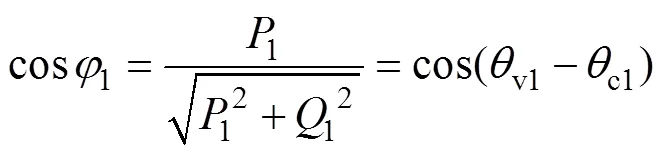
（2）3次谐波功率因数

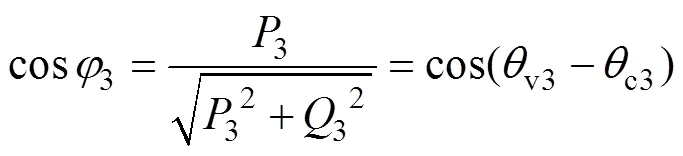
（3）总功率因数计算

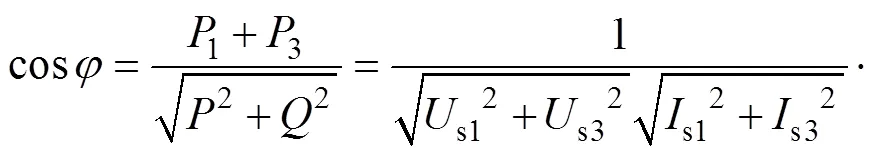
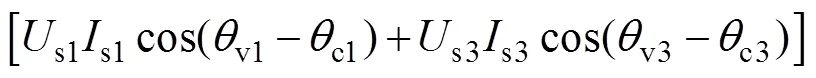
其中

s3=c3=

式中，1、3分别为基波、3次谐波有功功率；1、3分别为基波、3次谐波无功功率；分别为非正弦供电时总有功功率、无功功率；s1、s3分别为相电流基波、3次谐波分量有效值，c1、c3分别为相电流基波、3次谐波分量初始相位。

图2为注入、未注入3次谐波电流时电机总功率因数仿真结果。从图中可以看出，注入3次谐波电流后，使得电机的总功率因数略有降低（额定负载时，下降了约2%）。进一步分析可以发现，3次谐波电流注入对基波的功率因数影响不大，这从另一角度表明，注入的3次谐波电流产生的功率对电机的输出功率贡献很小。

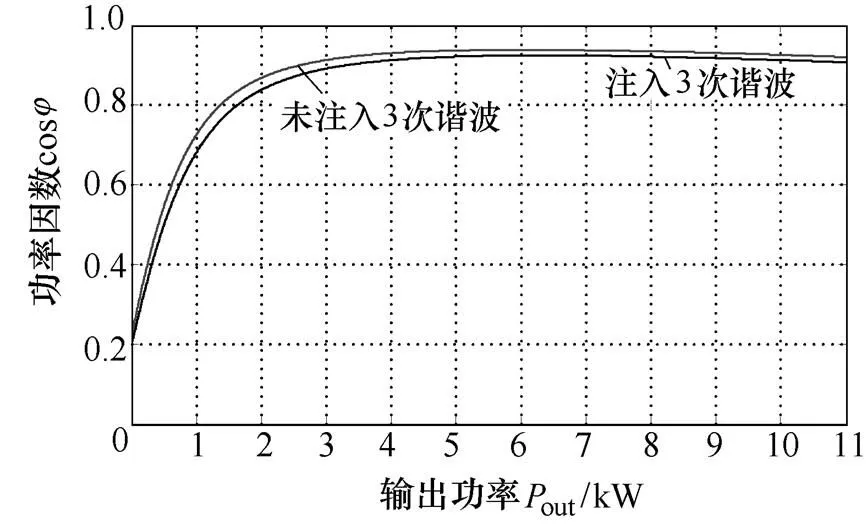
图2 注入、未注入3次谐波电流时电功率因数仿真曲线

图3为注入、未注入3次谐波电流时电机功率因数实验结果。对比图2中的仿真结果，两者基本一致。但由于仿真计算过程没有考虑电机的铁磁损耗、摩擦损耗等，故实验中电机功率因数比仿真计算小。另外，电机空载或者轻载时，铁磁损耗所占比例较高，特别是谐波分量产生的铁磁损耗较大。对比未注入谐波、注入谐波情形下，可以发现，电机空载或者轻载时，两者功率因数相差较大，随着负载的增大，铁磁损耗所占比例降低，两者功率因数相差越来越小。

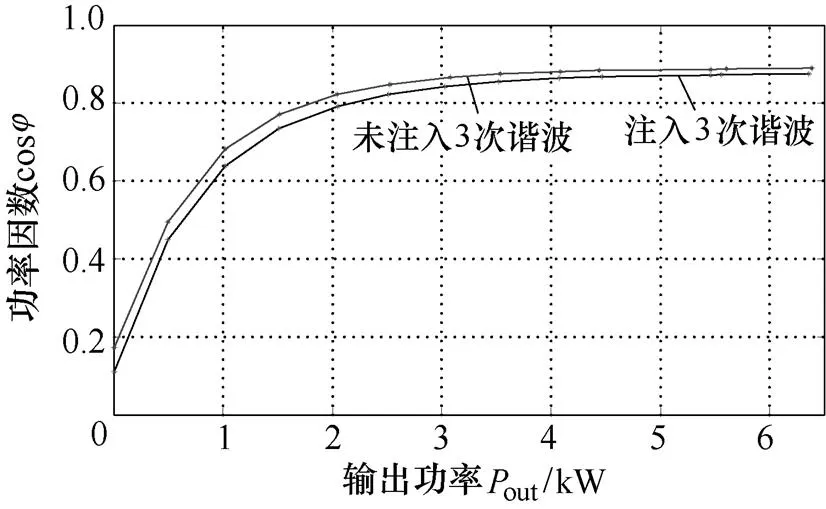
图3 注入、未注入3次谐波电流时电功率因数实验结果

2.3 电机效率变化

五相集中整距绕组感应电机T形等效电路如图4所示。

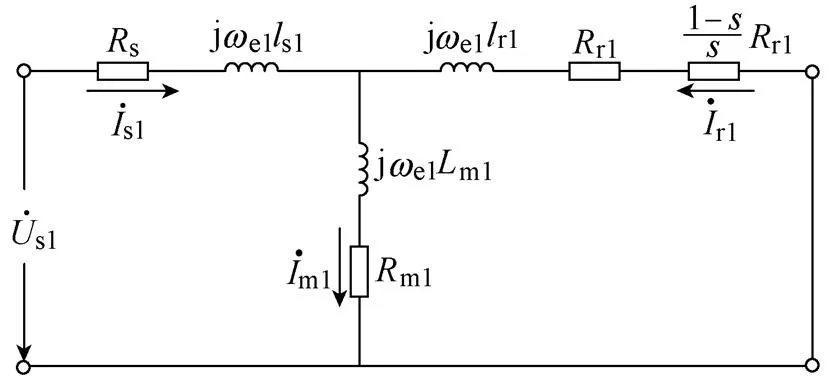
（a）基波空间

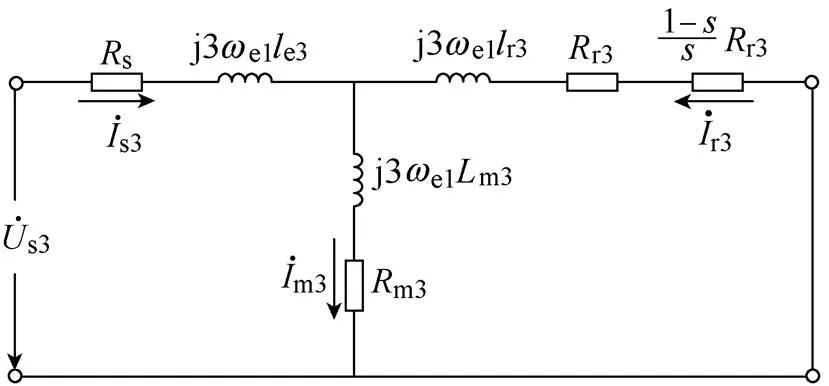
（b）3次谐波空间

图4 五相感应电机T形等效电路

Fig.4 T-form equivalent circuits of the five-phase induction motor

非正弦供电方式下，五相感应电机的效率表达式为

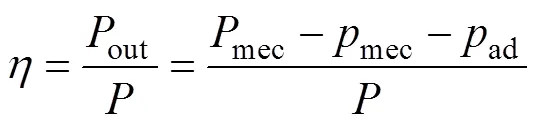
其中

式中，out为电机转轴输出机械功率；mec为电机总机械功率；em为总电磁功率；mec为机械损耗，ad为电机附加损耗；Cu_r1、Cu_r3分别为转子基波、3次谐波电流产生的铜耗；r1，r3为转子电流等效基波、3次谐波分量；表示电机的转差率。

式（9）中，r1、r3可通过上述电路的简化等效电路计算，表达式为

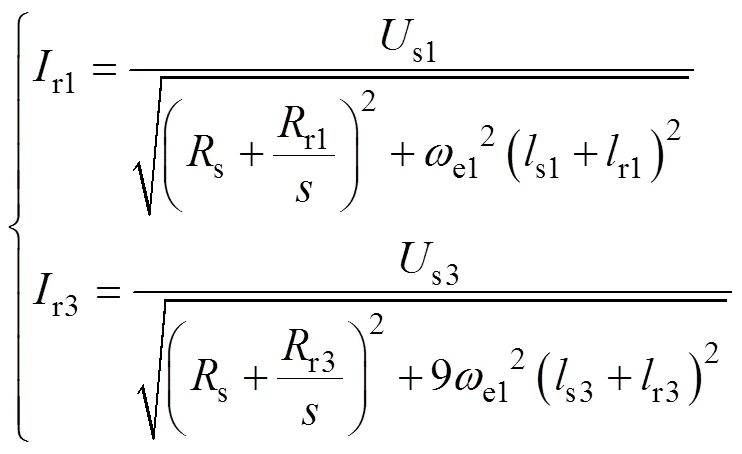
图5为注入、未注入3次谐波电流时电机效率随输出功率的变化曲线，从图中可以看出，与正弦电流供电方式相比，采用注入3次谐波电流的非正弦供电方式，使得电机效率略有降低（额定负载时，下降了约1%）。但是，随着电机负载的增大，两种供电方式的效率将变得很接近。

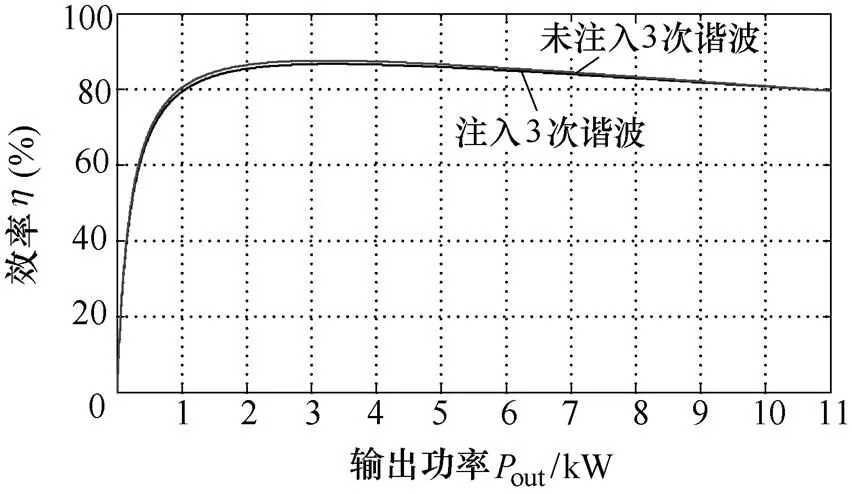
图5 注入、未注入3次谐波电流时电机效率仿真曲线

图6为注入、未注入3次谐波电流时电机效率实验结果。对比图5、图6仿真与实验结果，两者基本一致。同上一节分析，考虑铁磁损耗、摩擦损耗等影响，实验中电机效率比仿真计算小。对比未注入谐波、注入谐波情形下，可以发现，电机空载或者轻载时，两者效率相差较大，随着负载的增大，铁磁损耗所占比例降低，两者效率相差越来越小。

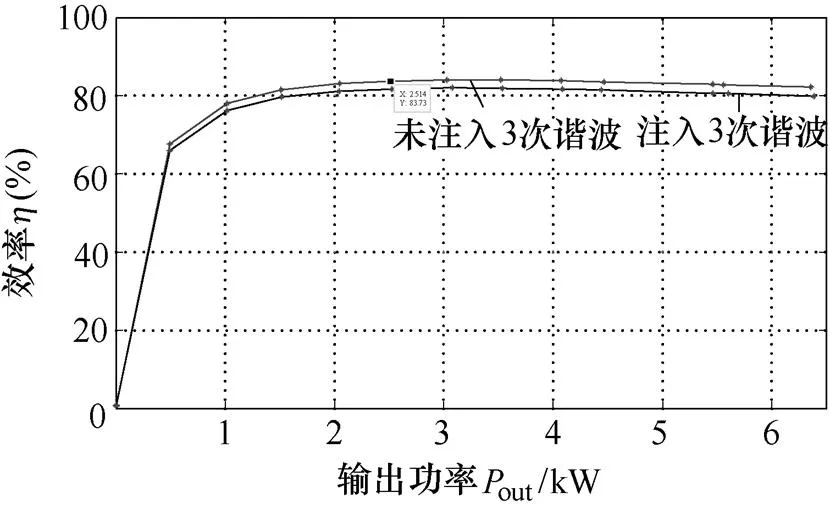
图6 注入、未注入3次谐波电流时电机效率实验结果

2.4 电磁转矩变化

采用3次谐波电流注入控制方法，可以增大电机的输出转矩。这主要表现在两个方面：一是3次谐波电流会产生电磁转矩，这部分转矩很小，大约是基波电流产生的电磁转矩1/36；二是注入3次谐波电流后，减小了气隙磁场幅值和电机局部饱和度，从保证气隙磁场幅值不变以充分利用铁心角度来看，则相当于可以增大基波电流幅值，从而提高基波产生的转矩，这是五相电机采用非正弦供电提高转矩密度的主要原因。下面将具体分析3次谐波电流注入对电机输出转矩能力的影响。

假设电机采用非正弦供电，使得气隙磁通密度为准方波（磁通密度基波与3次谐波相位关系为“峰谷”叠加），可令

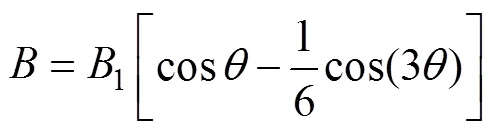
式中，1为气隙磁通密度基波分量幅值，为气隙磁通密度基波分量相位。

对式（11）求导，并令其为零。可以得到，气隙

由式（11），在保证气隙磁通密度峰值（最大值）不变的前提下，采用非正弦供电方式时，气隙磁通密度基波分量幅值是正弦供电方式时的倍。

由电机学理论，则此时反电动势、气隙磁链基波分量幅值也相应地为正弦供电方式时的倍（电流频率不变），定子电流各轴基波分量d1、q1也为正弦供电方式时的倍，故电机的输出电磁转矩将提高为原来的4/3倍（见式（3）），即与正弦供电方式相比，采用文中的非正弦供电可使得电机的最大输出电磁转矩提高了1/3。为了验证上面分析，对采用非正弦供电方式和正弦供电两种方式分别进行了仿真验证。

仿真条件：为了保证两种供电方式下气隙磁链（或气隙磁通密度）幅值是相等的，非正弦供电时的定子电流d1轴分量给定值为正弦供电时的倍，非正弦供电时的负载转矩为正弦供电时的4/3倍；电机转速从0起动到额定转速1 500r/min时间为1s；在=0～3s内，电机空载，在=3s突加额定负载。

仿真结果如图7所示。图7a～7d分别为正弦供电和非正弦供电方式下的反电动势、相电压、相电流和转速、转矩波形。图7a中，采用非正弦供电（注入3次谐波）下反电动势与正弦供电方式（注入3次谐波）下反电动势幅值是相等的，这表明两种供电方式下气隙磁通密度幅值也相等，同时，非正弦供电方式下，反电动势基波分量为正弦供电方式下反电动势幅值的倍；从图7b和7c可以看出，注入的3次谐波（电流或电压）所占比例较低，电机功率的提高主要是基波分量起作用；图7d中可以看出，3次谐波注入对电机的转速、转矩动态响应影响不大，但大幅提高了电机的电磁转矩（提高了约1/3）。

（a）反电动势

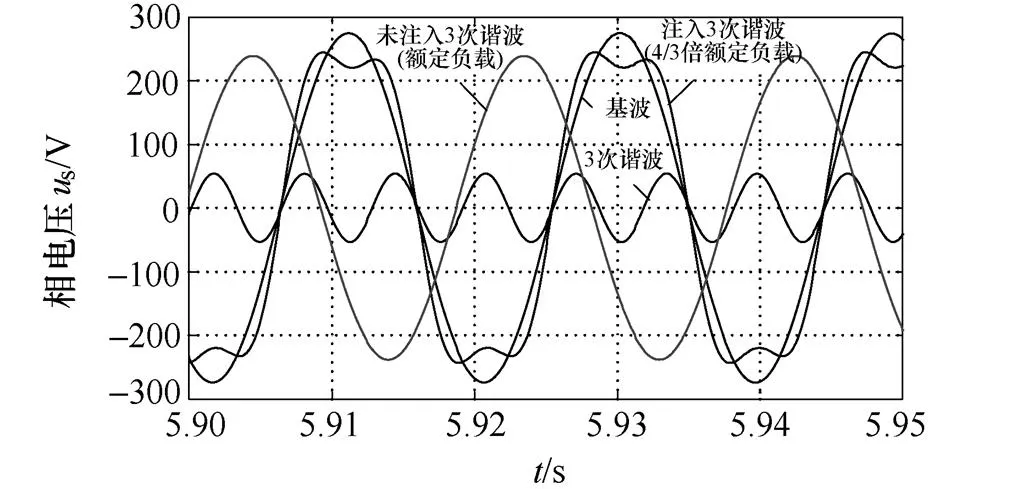
（b）相电压

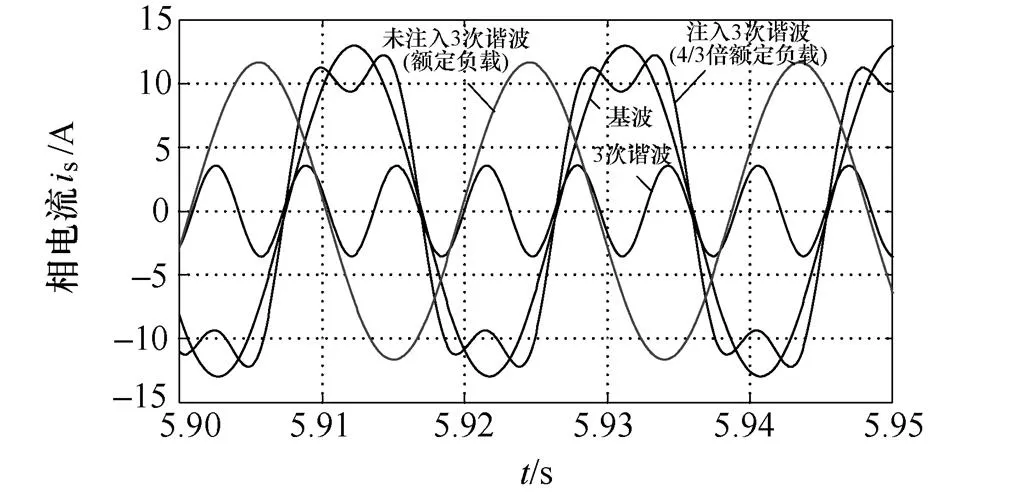
（c）相电流

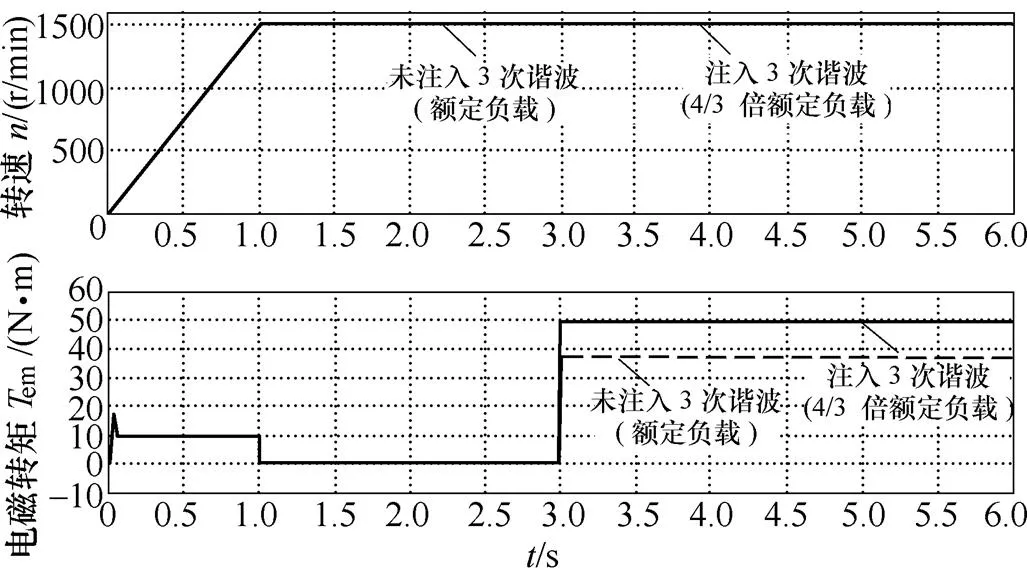
（d）起动过程中转速和转矩

图7 保持气隙磁通密度恒定、不同供电方式下仿真结果

Fig.7 Simulation results for constant air-gap magnetic density under different power supply modes

综上所述，通过注入3次谐波把合成的气隙磁通密度幅值提高到与正弦供电时气隙磁通密度相等，这将大大提高电机的铁磁材料利用率，从而提高电机的输出转矩。

3 实验验证

为了验证本文中理论，完成相关实验验证工作，搭建了系统实验平台，对实验室一台5.5kW五相集中感应电机进行了实验，电机参数见表1，实验平台如图8所示。系统平台主要有变压器、五相两电平H桥型变频器、五相感应电机、直流发电机及电阻柜等组成。其中，变频器控制器采用F2812+ FPGA的框架结构。

表1 五相感应电机参数

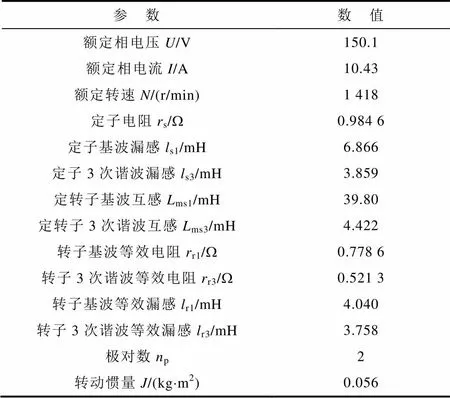
Tab.1 Parameters of five-phase induction motor

（a）H桥型变频器

（b）五相感应电机及直流发电机电阻负载

图8 五相感应电机调速系统实验平台

Fig.8 Five-phase induction motor speed-adjusting system experimental platform

图9和图10分别为未注入、注入3次谐波电流时滤波后相电压与相电流实验波形，对比两种不同情形下的实验结果，可以看出，在相同负载情况下，通过注入3次谐波，可以减小输出相电压幅值（峰值），换句话说，提高直流母线电压利用率。同时，通过3次谐波电流注入改善电机的气隙磁通密度，可以有效地提高电机的输出功率。

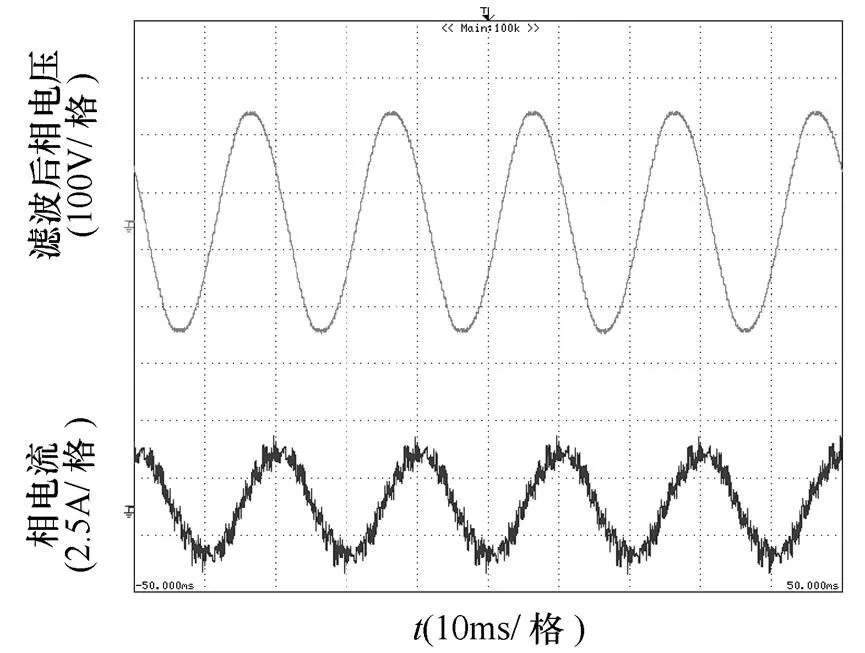
（a）空载

（b）额定负载

图9 未注入3次谐波时定子相电压、电流实验波形

Fig.9 Experimental waveforms of the stator phase voltage and current without third harmonic injected

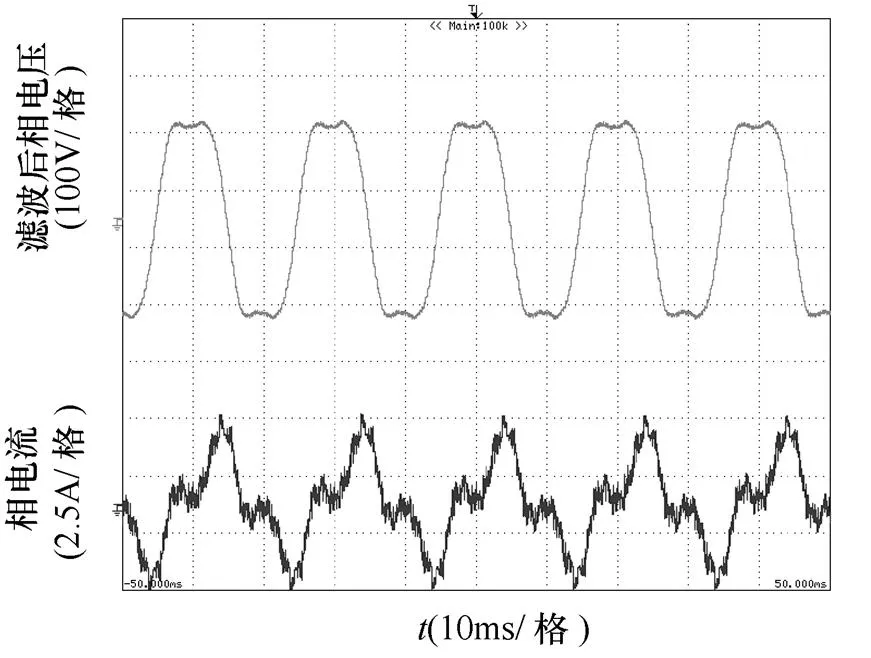
（a）空载

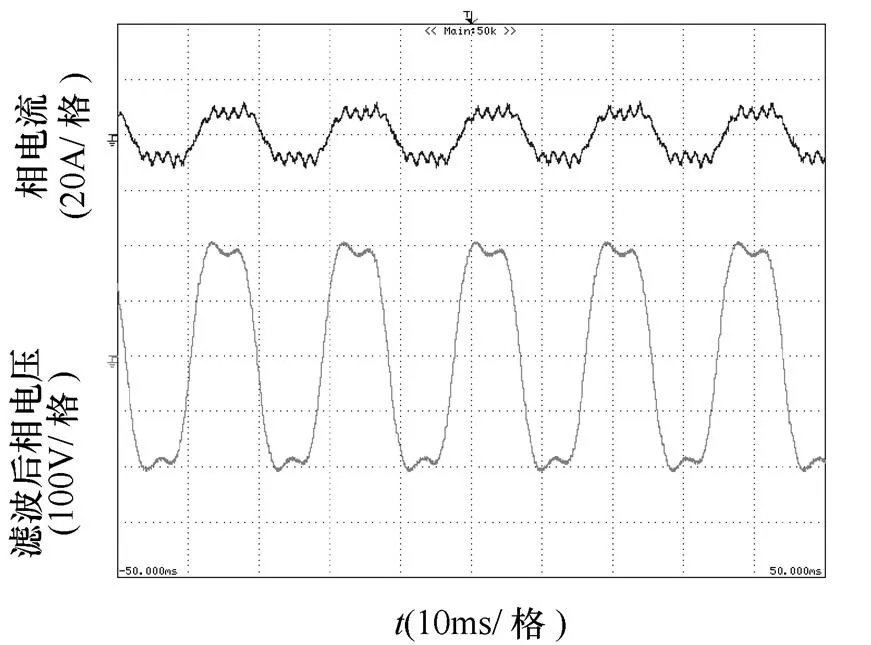
（b）额定负载

图10 注入3次谐波时定子相电压、电流实验波形

Fig.10 Experimental waveforms of the stator phase voltage and current with third harmonic injected

实际上，电机齿部和轭部均存在磁饱和效应，由电机设计理论，齿部磁通密度与气隙磁通密度呈正比关系，而轭部磁通密度与气隙磁通密度波形是积分的关系，采用文中提出的注入3次谐波电流方式，可以减小齿部磁通密度饱和度，却导致轭部饱和度增加。所以不可能将合成气隙磁通密度幅值提高到正弦供电时情形，即使得气隙磁通密度3次谐波分量幅值为基波的1/6，而是应选择小于1/6的值。因此，实际过程中，电磁转矩提高幅度不可能达到1/3，具体与电机设计及所选铁磁材料特性有关。

图11为注入三次谐波、电机过载约1.15倍额定负载时，定子相电压及电流波形。若再提高电机所带负载，电机气隙磁通密度会发生畸变，电流谐波增大，电机损耗将大幅增大，从而会导致电机效率等性能降低。

图11 带1.15倍额定负载时定子相电压、电流实验波形

4 结论

本文在3次谐波注入控制策略研究基础上，从母线利用率、功率因数、效率、转矩等性能指标出发，分析3次谐波电流注入对系统的影响。可以得到以下结论。

1）可以大幅度地提高直流母线利用率，空载时提高了约15.2%，额定负载时提高了12.3%。

2）系统的功率因数和电机效率略有下降，额定负载时分别为2%、1%。

3）电机输出电磁转矩大幅提高，在保持气隙磁通密度幅值前提下，理论上电磁转矩提高可达33.3%。

综合考虑以上分析结果，有效证明了3次电流注入对于改善系统运行性能是切实可行的。

参考文献：

[1] 刘自程, 郑泽东, 彭凌, 等. 船舶电力推进中十五相感应电机同轴运行及容错控制策略[J]. 电工技术学报, 2014, 29(3): 65-74.

Liu Zicheng, Zheng Zedong, Peng Ling, et al. Fixed ioint double fifteen-phase induction motor control and fault-tolerant control in ship propulsion system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 65-74.

[2] 方程, 许海平, 薛劭申, 等. 直驱型多相永磁同步电机转矩脉动及损耗特性[J]. 电工技术学报, 2014, 29(5): 149-159.

Fang Cheng, Xu Haiping, Xue Shaoshen, et al. Torque ripple and losses of direct-drive multi-phase permanent magnet synchronous machines[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(5): 149-159.

[3] 胡维昊, 王跃, 李明烜, 等. 基于MRAS的多相永磁直驱型风力发电系统无速度传感器控制策略研究[J]. 电力系统保护与控制, 2014, 42(23): 118-124.

Hu Weihao, Wang Yue, Li Mingxuan, et al. Research on sensorless control strategy of direct drive multi- phase PMSG wind power generation system based on MRAS[J]. Power System Protection and Control, 2014, 42(23): 118-124.

[4] 姜杰, 许宏, 陈贵文, 等. 电压跌落时感应电动机反馈电流计算及转速影响研究[J]. 电力系统保护与控制, 2014, 42(23): 31-37.

Jiang Jie, Xu Hong, Chen Guiwen, et al. Induction motor feedback current calculation and speed factor analysis[J]. Power System Protection and Control, 2014, 42(23): 31-37.

[5] Zhao Y F, Lipo T A. Modeling and control of a multi- phase induction machine with structural unbalance, part I: machine modeling and multi-dimensional current regulation[J]. IEEE Transactions on Energy Conversion, 1996, 11(3): 570-577.

[6] Zhao Y F, Lipo T A. Modeling and control of a multi-phase induction machine with structural unbalance part II: field-oriented control and experimental veri- fication[J]. IEEE Transactions on Energy Conversion, 1996, 11(3): 578-584.

[7] 吴新振, 王祥珩, 罗成. 多相异步电机谐波电流与谐波磁动势的对应关系[J]. 清华大学学报(自然科学版), 2005, 45(7): 865-868.

Wu Xinzhen, Wang Xiangheng, Luo Cheng. Relation-ship between harmonic currents and harmonic magneto- motive forces in multi-phase induction machines[J]. Journal of Tsinghua University (Science and Tech- nology), 2005, 45(7): 865-868.

[8] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机气隙磁势分析[J]. 中国电机工程学报, 2009, 29(15): 88-94.

Wang Dong, Wu Xinzhen, Ma Weiming, et al. Air- gap MMF analysis of fifteen-phase induction motor with non-sinusoidal supply[J]. Proceedings of the CSEE, 2009, 29(15): 88-94.

[9] 王东, 马伟明, 郭云珺, 等. 基于非正弦供电方式的多相感应电动机建模[J]. 电工技术学报, 2010, 25(2): 6-14.

Wang Dong, Ma Weiming, Guo Yunjun, et al. Modelling of multiphase induction motor with non— sinusoidal supply[J]. Transactions of China Electro- technical Society, 2010, 25(2): 6-14.

[10] 杨家强, 高健, 金玉龙, 等. 基于矢量控制的多相感应电机电子变极调速技术[J]. 电工技术学报, 2014, 29(3): 96-102.

Yang Jiaqiang, Gao Jian, Jin Yulong, et al. Electronic pole-changing speed adjusting technology of multi- phase induction motors based on vector control[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 96-102.

[11] 张杰, 柴建云, 孙旭东, 等. 双三相异步电机电流预测控制算法[J]. 电工技术学报, 2015, 30(9): 12-21.

Zhang Jie, Chai Jianyun, Sun Xudong, et al. Predictive current control methods for dual three phase induction machine[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 12-21.

[12] Zheng L B, Fletcher J E, Williams B W, et al. Dual-plane vector control of a five-phase induction machine for an improved flux pattern[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1996-2005.

[13] Abdel-Khalik A S, Masoud M, Williams B. Improved flux pattern with third harmonic injection for multiphase induction machines[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1563-1578.

[14] Mario J D, Francisco S, Manuel R A. Bifurcation analysis of five-phase induction motor drives with third harmonic injection[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 2006-2014.

[15] 朱鹏, 张晓锋, 乔鸣忠, 等. 基于双平面同步旋转变换五相感应电机气隙磁场间接矢量控制[J]. 中国电机工程学报, 2013, 33(27): 112-119.

Zhu Peng, Zhang Xiaofeng, Qiao Mingzhong, et al. Indirect vector control for air-gap magnetic field of five-phase induction motor through dual-plane synch- ronized rotation transformation[J]. Proceedings of the CSEE, 2013, 33(27): 112-119.

The Effects of Third Harmonic Current Injection on Operation Performance of Five-Phase Induction Motor

11121

（1. College of Electric Engineering Naval University of Engineering Wuhan 430033 China;2. College of Optoelectronics Engineering Chongqing University of Posts and Telecommunications Chongqing 400065 China）

The air-gap magnetic density of five-phase induction motor with concentrated full-pitch windings structure can be improved by harmonic injection, and accordingly the power density of five-phase induction motor will increase. Based on the third-harmonic injected control strategy of five-phase induction motor, the effects of third harmonic injection on some important evaluating indexes of the system were analyzed, such as the DC-bus voltage utilization ratio, power ratio, efficiency, torque density, and so on. Finally, the experimental platform of five-phase induction motor system was built. The experiments were carried out on a 5.5kW, five-phase concentrated full-pitch windings induction motor. The results verify that the operation performance of five-phase induction motor system can be improved effectively by third harmonic injection with special varied regulation.

Air-gap magnetic flux density, voltage utilization ratio, power ratio, efficiency, torque density

TM304.1

朱 鹏 男，1984年生，博士，讲师，研究方向为电力电子与电力传动等。

E-mail: zhupeng840608@163.com（通信作者）

乔鸣忠 男，1971年生，教授，博士生导师，研究方向为电力系统自动化、船舶电力推进电机及其控制。

E-mail: qiaomingzhong@126.com

2016-02-24 改稿日期 2016-05-08

国家自然科学基金资助项目（51407188、51277177、51307180）。