基于Schweizer-Sklar三角范数簇的反向三I算法的鲁棒性

罗敏霞，王雅萍

（中国计量学院理学院，浙江杭州310018）

基于Schweizer-Sklar三角范数簇的反向三I算法的鲁棒性

罗敏霞，王雅萍

（中国计量学院理学院，浙江杭州310018）

Schweizer-Sklar三角范数具有很好的柔性，使得基于柔性化算子的模糊推理算法有良好的属性.本文基于Minkowski距离标准研究Schweizer-Sklar算子簇的性质及模糊推理算法的鲁棒性.证明了Schweizer-Sklar三角范数簇关于参数m是单调递减的；Schweizer-Sklar三角余范簇关于参数m是单调递增的；并且给出了Schweizer-Sklar三角余范簇、三角范数簇及其诱导的剩余蕴涵簇的扰动；证明了m∈（0，∞）时，Schweizer-Sklar剩余蕴涵簇（包含Lukasiewizc蕴涵）均适合用于模糊推理.进一步证明了：当m∈（0，∞）时，基于Schweizer-Sklar剩余蕴涵簇的FMP-反向三I算法具有鲁棒性；当m∈（0，∞）时，基于Schweizer-Sklar剩余蕴涵簇的FMT-反向三I算法具有鲁棒性.

Schweizer-Sklar三角范数；反向三I算法；Minkowski距离；鲁棒性

1 引言

自从Zadeh于1965年提出模糊集的概念［1］，将原来对命题的非此即彼的判断方法推广到用整个［0，1］区间上的值来表示真值度，模糊理论就被广泛的应用于数学和其他应用领域，在实践中越来越多的人使用具有优势的模糊理论方法［2，3］.许多学者从不同的角度研究了命题逻辑系统［4］进而研究模糊推理的应用.模糊推理中的最基本推理模型是模糊假言推理（FMP）问题和模糊反驳推理（FMT）问题［5］：

FMP：给定规则A→B并输入A*，输出B*；

FMT：给定规则A→B并输入B*，输出A*；

其中：A，A*∈F（X），B，B*∈F（Y），F（U）表示论域U的全体模糊子集构成的集合.

针对这一问题，Zadeh提出了CRI（Compositional Rule of Inference）模糊推理方法［6］，而CRI方法中合成运算带有随意性，缺少严格的逻辑依据.1999年王国俊教授首先提出了基于R0算子的全蕴涵三I算法［5］，该算法避免了CRI方法中合成运算的随意性，并给出此模糊推理算法的严格的逻辑基础.裴道武教授研究了基于左连续三角范数诱导的剩余蕴涵的三I算法，并且建立了基于MTL逻辑系统的三I算法的可靠逻辑基础［7，8］.罗敏霞教授选取一类更具柔性，更贴合实际应用的三角范数簇，讨论了基于Schweizer-Sklar剩余蕴涵簇的全蕴涵三I算法以及其连续性［9］.

宋士吉等首次提出了反向三I算法［10］，其基本思想是：已知A∈F（X）和B∈F（Y），并且A*∈F（X）（或者B*∈F（Y）），对一切x∈X，y∈Y，寻找最优的B*∈F（Y）（或者A*∈F（X）），使得A*→B*最大程度的支持A→B，即使得（A*（x）→B*（y））→（A（x）→B（y））达到最大可能值.

罗敏霞等进一步给出基于Schweizer-Sklar剩余蕴涵簇反向三I算法［11］，为实际应用提供更具柔性的模糊推理算法.

在模糊控制中，实际的模糊推理模型很容易被不同的噪声扰动.在模糊理论下分析鲁棒性问题是非常有意义的［12］，模糊推理的鲁棒性是为了测量在模糊推理中一定的输入误差可以引起多大的输出误差.度量误差的测量标准有相似度、Hamming距离、Euclidean距离、Chebyshev距离、平均扰动、δ-扰动和（T，δ）-扰动等等［13～16］，王国俊和段景瑶在文献［15］提出正则度量的概念，给出估算模糊推理鲁棒性另一种度量标准.这些方法各有利弊，因为往往两个模糊集在一种距离的定义下有较小的扰动，而在另一种距离的定义下有较大的扰动，针对该问题，戴松松等人在文献［17］中应用更具有普遍意义的规范化Minkowski距离研究模糊连接词及CRI模糊推理算法的扰动，得到较理想的结论.本文利用规范化Minkowski距离标准研究Schweizer-Sklar算子簇的扰动及基于Schweizer-Sklar剩余蕴涵簇的反向三I算法的鲁棒性.

2 预备知识

定义 1［18］设T是［0，1］上的二元运算，T：［0，1］2→［0，1］，任意x，y，z∈［0，1］，如果满足下列条件：

（T1）T（x，y）=T（y，x）；

（T2）T（x，T（y，z））=T（T（x，y）z）；

（T3）当y≤z时，T（x，y）≤T（x，z）；

（T4）T（x，1）=x.

则称T是一个三角范数.

设S是［0，1］上的二元运算，S：［0，1］2→［0，1］，任意x，y，z∈［0，1］，如果满足（T1），（T2），（T3），且满足（S4）S（x，0）=x，则称S是一个三角余范.

定义2［18］Schweizer-Sklar三角范数簇Tm（x，y）：［0，1］2→［0，1］，且对任意x，y∈［0，1］，m∈R，

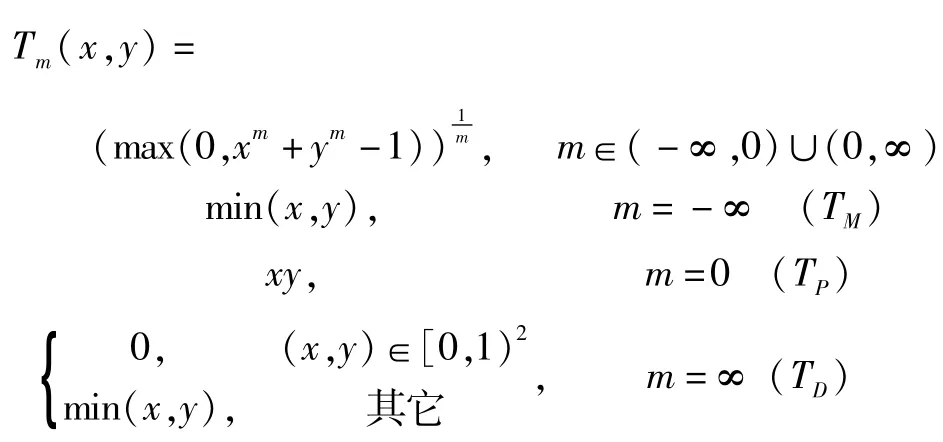
特别地，当m=1时，TL（x，y）=max（0，x+y-1）是Lukasiewizc三角范数.

定义3［18］Schweizer-Sklar三角余范簇Sm（x，y）：［0，1］2→［0，1］，且对任意x，y∈［0，1］，m∈R，

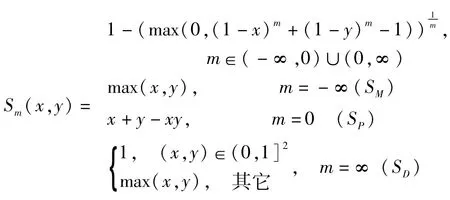
特别地，当m=1时，SL（x，y）=min（x+y，1）是Lukasiewizc三角余范.

定义4［19，20］Schweizer-Sklar三角范数簇诱导的剩余蕴涵簇Im（x，y）；［0，1］2→［0，1］，且对任意x，y∈［0，1］，m∈R，

特别地，当m=1时，IL（x，y）=min（1，1-x+y）是Lukasiweize蕴涵.

定义 5［17］假设A和B是论域X=｛x1，…，xn｝上的模糊集，则称dp（A，B）=为模糊集A和B的规范化Minkowski距离，其中p∈［1，∞］为参数.

定义6 设f：［0，1］2→［0，1］，ε∈［0，1］，设X=是论域上的模糊集与是论域上的模糊集

称为函数f在（X，Y）的（ε1，ε2）-灵敏度.其中

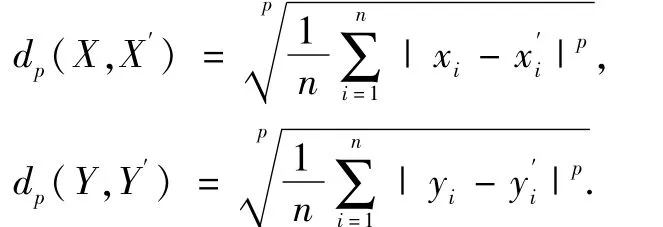
p

定义7

定义8 设

如果

称函数f由（ε1，ε2）输入引起的≤ε的输出扰动.引理1［21］假设x，y＞0且x≠y，那么

rxr-1（x-y）＞xr-yr＞ryr-1（x-y）（r＜0或r＞1）

rxr-1（x-y）＜xr-yr＜ryr-1（x-y）（0＜r＜1）

rxr-1（x-y）=xr-yr=ryr-1（x-y）（r=0或1，x=y）引理2［22］令I是一个有限指标集，那么

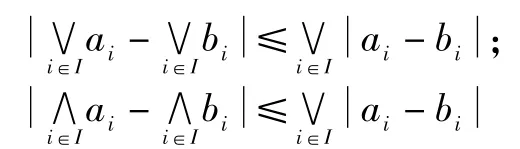
引理3 假设x，y∈［0，1］且r＞1，那么|xr-yr|≤r|x-y|.由引理1可得该结论.

证明：由于f（x）是［c，b］上的可导函数，故

因为f（x）在［c，b］连续，由Lagrange中值定理，至少存在一点ξ∈（c，b）使得

类似的，如果f（c）-f（b）≥0，应用Lagrange中值定理，至少存在一点ξ∈（c，b）使得

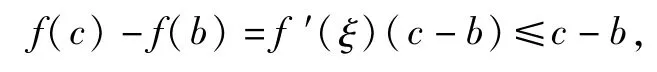
引理 6（Minkowski不等式） 令（a1，a2，…，an），（b1，b2，…，bn）∈Rn，且1≤p＜∞.那么

引理7［23］设A，B∈（0，1）或 A，B∈（1，+∞），如果A+B＞1，则（A+B-1）Ln（A+B-1）≥ALnA +BLnB.

命题1［11］假设FMP问题中蕴涵算子是Schweizer-Sklar三角范数簇诱导的剩余蕴涵簇，那么FMP-反向三I解的表达式为：对x∈X，y∈Y，

命题2［11］假设 FMT问题中的蕴涵算子是 Schweizer-Sklar三角范数簇诱导的剩余蕴涵Im（x，y）（m＞0），FMT-反向三 I解A*的表达式为：对x∈X，y∈Y，

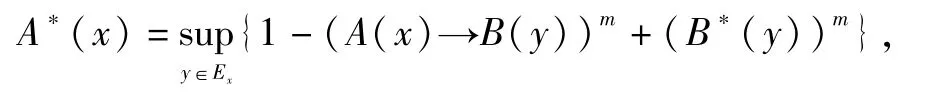
其中，Ex=｛y∈Y|m＞0，B*（y）∨（A（x）→B（y））＜1，B*（y）＜（A（x）→B（y））｝

3 Schweizer-Sklar模糊连结词的性质及其扰动

命题3 Schweizer-Sklar三角范数簇Tm（x，y）关于m是单调递减的，且

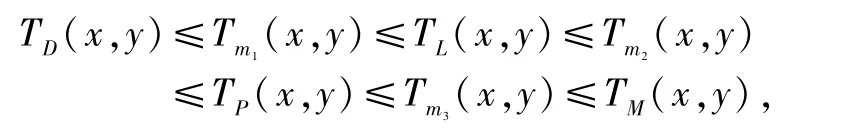
其中，m1∈（1，+∞），m2∈（0，1），m3∈（-∞，0）.

证明：

（1）当m∈（1，+∞）时，TD（x，y）≤Tm（x，y）≤TL（x，y），且Tm（x，y）关于m是单调递减的.

先证明TD（x，y）≤Tm（x，y）.当max（x，y）=1时，不妨假设y=1，则 TD（x，y）=x=Tm（x，y）；其他情形TD（x，y）=0≤Tm（x，y）.

下证 Tm（x，y）≤TL（x，y）（m∈（1，+∞）），且Tm（x，y）（m∈［1，+∞））关于m是单调递减的.

当m∈（1，+∞）时，∀x，y∈（0，1），xm+ym-1≤x +y-1.当xm+ym≤1时，Tm（x，y）=0≤TL（x，y）；当 xm+ym＞1时，则Tm（x，y）=xm+ym-1.

设 Tm（x，y）：［1，+∞）→R+，Tm（x，y）= （xm+ym-1）1/m是关于x，y，m的一个多元函数，则

从而，

（2）当（m∈（0，1）时，TL（x，y）≤Tm（x，y）≤TP（x，y），且Tm（x，y）关于m是单调递减的.

（3）当m∈（-∞，0）时，TP（x，y）≤Tm（x，y）≤TM（x，y），且Tm（x，y）关于m是单调递减的.

类似（1）的证明，可证（2）与（3）的结论.

注1 由命题3我们得到含有参数的三角范数簇与参数m之间的关系，且四种常用的三角范数包含在其中，从而得到它们之间的关系［24］：

TD（x，y）≤TL（x，y）≤TP（x，y）≤TM（x，y）.

命题4 Schweizer-Sklar三角余范数簇关于m单调递增，即

其中，m1∈（-∞，0），m2∈（0，1），m3∈（1，∞）.

命题4可类似于命题3证明.

注2 由命题4我们得到含有参数的三角余范簇与参数m之间的关系，且四种常用的三角余范包含在其中，从而得到它们之间的关系［24］：

命题5 假设 dp（A，A′）≤ε1，dp（B，B′）≤ε2，那么dp（Tm（A，B），Tm（A′，B′））≤

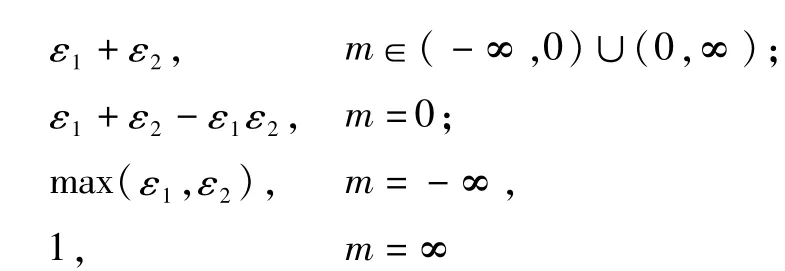
证明：假设

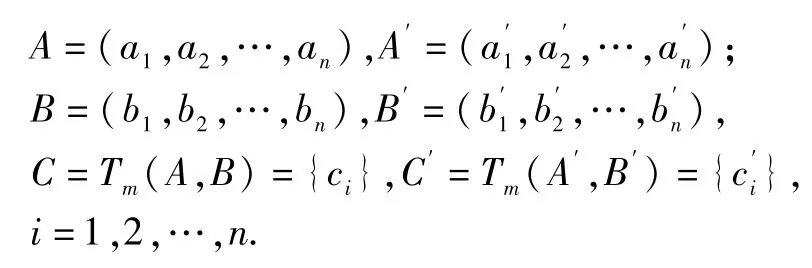
当m≥1时，

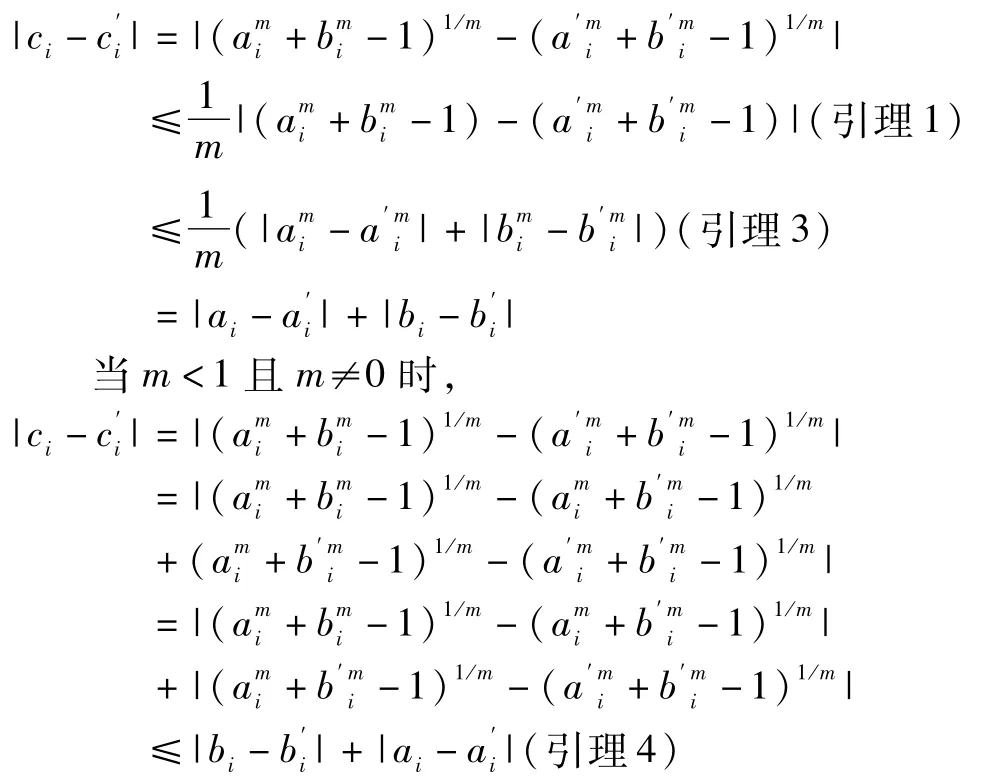
则可得到，

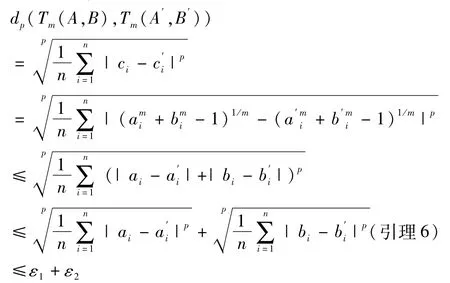
当m=0时，

其它情形类似可证明.

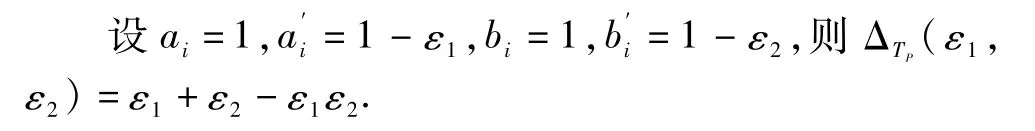
当m=-∞时，

注3 本命题给出一簇含参数的三角范数的扰动.特别当m=0时，乘积三角范数的最大灵敏度是ε1+ε2-ε1ε2；当 m=1时，Lukasiewicz三角范数的最大灵敏度是ε1+ε2；当m=-∞时，极小三角范数的最大灵敏度是max（ε1，ε2）；当m=∞时，突变三角范数的最大灵敏度是1，这种情形不具有鲁棒性.

命题6 假设 dp（A，A′）≤ε1，dp（B，B′）≤ε2，那么

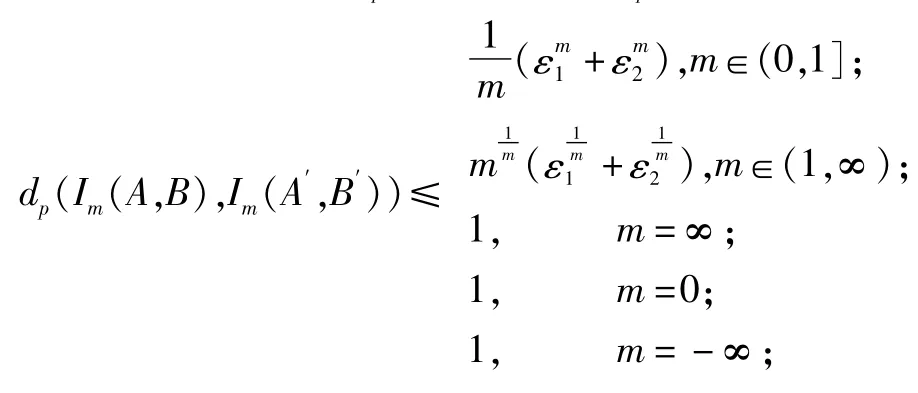
命题6可类似于命题5证明.

注4 当m∈（0，∞），含参数的蕴涵算子簇具有鲁棒性，适合用于模糊推理；特别当m=1时，Lukasiewicz蕴涵算子的最大灵敏度是ε1+ε2.另外，当m=0时，Goguen蕴涵算子的最大灵敏度是1；当m=-∞时，Godel蕴涵的最大灵敏度都是1；当m=∞时，突变蕴涵的最大灵敏度是1，这三种情形都不具有鲁棒性，从而均不适合用于模糊推理.

命题7 假设 dp（A，A′）≤ε1，dp（B，B′）≤ε2，那么dp（Sm（A，B），Sm（A′，B′））

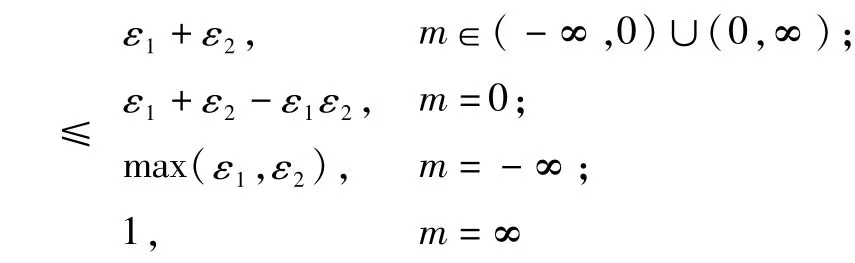
证明：假设

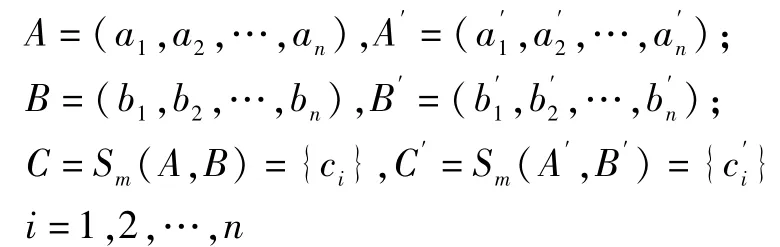
当m≥1，

当m≤1且m≠0，

则可得到，

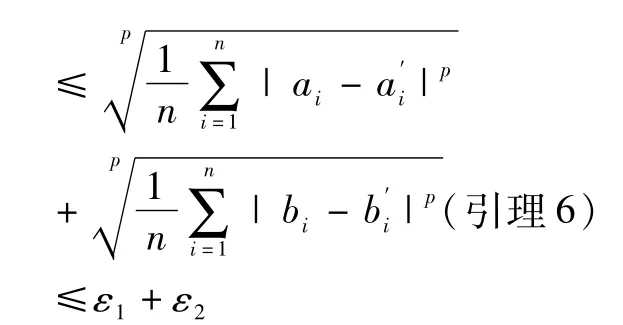
当m=0时，

其它情形类似可证明.

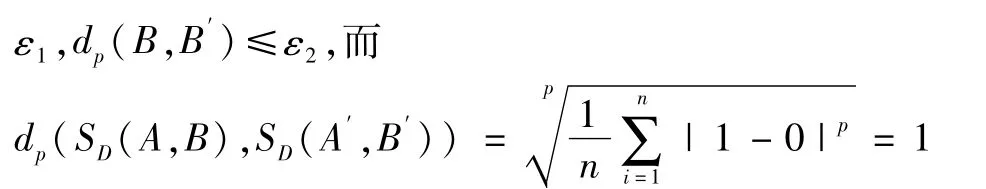
注5 本命题给出一簇含参数的三角余范的扰动.特别当m=0时，概率和三角余范的最大灵敏度是ε1+ ε2-ε1ε2；当m=1时，Lukasiewicz三角余范的最大灵敏度是ε1+ε2；当m=-∞时，极大三角余范的最大灵敏度是max（ε1，ε2）；当m=∞时，突变和三角余范的最大灵敏度是1，这种情形不具有鲁棒性.

4 基于Schweizer-Sklar剩余蕴涵簇的反向三I算法的鲁棒性

定理1 假设 dp（A，A′）≤ε1，dp（B，B′）≤ε2，dp（A*，A′*）≤ε3，B*和B′*是FMP-反向三I解（m∈（0，∞）），则

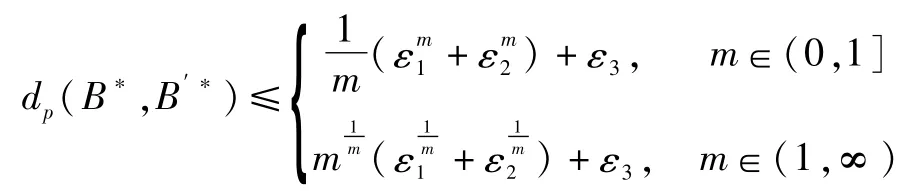
证明：当m∈（0，∞）时，令

则由命题6，

再由命题1和命题5，

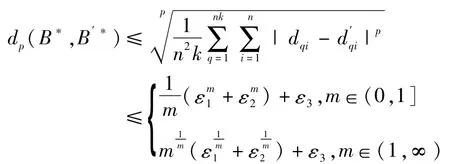
注6 本定理给出基于一簇含参数的蕴涵算子的FMP-反向三I算法的鲁棒性，特别当m=1时，基于Lukasiewicz蕴涵算子的FMP-反向三I解的最大灵敏度是ε1+ε2+ε3.由命题6可知，其它三种常用的蕴涵运算均不适合做模糊推理连接词.

定理2 假设 dp（A，A′）≤ε1，dp（B，B′）≤ε2，dp（B*，B′*）≤ε3，A*和 A′*是FMT-反向三I解（m∈（0，∞）），则

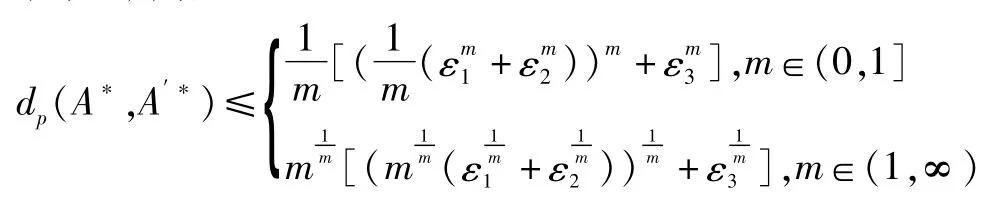
证明：当m＞0时，令

由命题6，

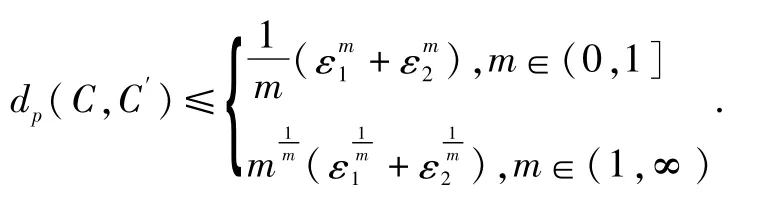
再由命题2与命题6，

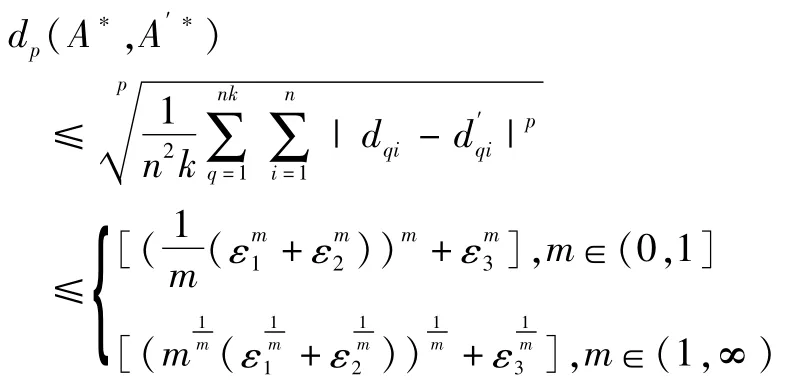
5 结论

本文以Minkowski距离为度量标准，研究Schweizer-Sklar三角范数簇、三角余范簇及其诱导的剩余蕴涵簇的单调性及其扰动.证明了Schweizer-Sklar三角范数簇关于参数m是单调递减的；Schweizer-Sklar三角余范簇关于参数m是单调递增的；并且给出四种著名的三角范数及三角余范的序.给出了Schweizer-Sklar三角余范簇、三角范数簇及其诱导的剩余蕴涵簇的扰动；证明了m∈（0，∞）时，Schweizer-Sklar剩余蕴涵算子簇具有很好的鲁棒性，均适合用于模糊推理.文献［11］给出了的基于Schweizer-Sklar剩余蕴涵簇反向三I算法解的一般表达式，在此基础上，结合Schweizer-Sklar三角范数簇及其诱导的剩余蕴涵簇的扰动研究得到，当m∈（0，∞）时，基于Schweizer-Sklar剩余蕴涵簇的 FMP-反向三I算法具有鲁棒性；当m∈（0，∞）时，基于Schweizer-Sklar剩余蕴涵簇的FMT-反向三I算法具有鲁棒性.因其为模糊控制等应用提供了可靠的理论依据，使得基于柔性Schweizer-Sklar三角范数簇的模糊推理算法具有更广泛、更实际的应用前景.

［1］Zadeh L A.Fuzzy sets［J］.Information and Control，1965，8（3）：338-353.

［2］陈卫东，朱奇光.基于模糊算法的移动机器人路径规划［J］.电子学报，2011，39（4）：971-974. CHEN Wei-dong，ZHU Qi-guang.Mobile robot path planning based on fuzzy algorithms［J］.Acta Electronica Sinica，2011，39（4）：971-974.（in Chinese）

［3］袁学海，李洪兴，杨雪.基于模糊变换的模糊系统和模糊推理建模法［J］.电子学报，2013，41（4）：674-680. YUAN Xue-hai，LI Hong-xing，YANG Xue.Fuzzy system and fuzzy inference modeling method based on fuzzy transformation［J］.Acta Electronica Sinica，2013，41（4）：674-680.（in Chinese）

［4］罗敏霞，姚宁.L*系统中公式的语构程度化方法［J］.电子学报，2011，39（2）：424-428. LUO Min-xia，YAO Ning.Syntactic graded method of formulas in the system L*［J］.Acta Electronica Sinica，2011，39（2）：424-428.（in Chinese）

［5］王国俊.模糊推理的全蕴涵三I算法［J］.中国科学（E辑），1999，29（1）：43-53.

［6］Zadeh L A.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems，Man，and Cybernetics，1973，3（1）：28 -44.

［7］Pei D W.Unified full implication algorithms of fuzzy reasoning［J］.Information Sciences，2008，178（2）：520-530.

［8］Pei D W.Formalization of implication based fuzzy reasoning method［J］.International Journal of Approximate Reasoning，2012，53（5）：837-846.

［9］Luo M X，Yao N.Triple I algorithms based on Schweizersklar operators in fuzzy reasoning［J］.International Journal of Approximate Reasoning，2013，54（5）：640-652.

［10］宋士吉，吴澄.模糊推理的反向三I算法［J］.中国科学（E辑），2002，32（2）：230-246.

［11］罗敏霞，桑倪.基于Schweizer-Sklar三角范数簇诱导的剩余蕴涵簇的反向三I算法［J］.智能系统学报，2012，7 （6）：494-499. LUO Minxia，SANG Ni.The reverse triple I algorithms based on a class of residual implications induced by the family of Schweizer-Sklar t-norms［J］.CAAI Transactions on Intelligent Systems，2012，7（6）：494-499.（in Chinese）

［12］陈明，陈武凡，冯前进，杨丰.基于互信息量和模糊梯度相似性的医学图像配准［J］.电子学报，2003，31（12）：1835-1838. CHEN Ming，CHEN Wu-fan，FENG Qian-jin，YANG Feng.Medical image registration based on mutual information and fuzzy gradient similarity［J］.Acta Electronica Sinica，2003，31（12）：1835-1838.（in Chinese）

［13］Dai S S，Pei D W，Guo D H.Robustness analysis of full implication inference method［J］.Approximate Reasoning，2013，54（5）：653-666.

［14］Li Y F，Qin K Y，He X X.Robustness of fuzzy connectives and fuzzy reasoning［J］.Fuzzy Sets and Systems，2013，225（8）：93-105.

［15］Wang G J，Duan J Y.On robustness of the full implication triple I inference method with respect to finer measurements［J］.Approximate Reasoning，2014，55（3）：787 -796.

［16］Hung W L，Yang M S.Similarity measures of intuitionistic fuzzy sets based on LPmetric［J］.International Journal of Approximate Reasoning，2007，46（1）：120-136.

［17］Dai S S，Pei D W，Wang S M.Perturbation of fuzzy sets and fuzzy reasoning based on normalized Minkowski distance［J］.Fuzzy Sets and Systems，2012，189（1）：63 -73.

［18］Klement E P，Mesiar R，Pap E.Triangular Norms［M］. Dordrecht：Kluwer Academic，2000.

［19］Whalen T.Parameterized R-implications［J］.Fuzzy Sets and Systems，2003，134（2）：231-281.

［20］He H C，Wang H，Liu Y H.Principle of Universal Logics ［M］.Beijing：Science Press，2006.

［21］Hardy G H，Littlewood J E，Polya G.Inequalities（2nd edition）［M］.Cambrige：Cambridge University Press，1952.

［22］徐蔚鸿，谢中科，杨静宇，叶有培.两类模糊推理算法的连续性和逼近性［J］.软件学报，2004，15（10）：1485 -1492. XU Wei-Hong，XIE Zhong-Ke，YANG Jing-Yu，YE You-Pei.Continuity and approximation properties of two classes of algorithms for fuzzy inference［J］.Journal of Software，2004，15（10）：1485-1492.（in Chinese）

［23］罗敏霞，何华灿.泛逻辑学语构理论［M］.北京：科学出版社，2010.

［24］Wang X Z，Ruan D，Kerre E E.Mathematics of Fuzziness—Basic Issues［C］.Heidelberg：Springer，2009.

罗敏霞 女，1964年生于山西运城，教授、博士、硕士生导师.中国人工智能学会人工智能基础专业委员会常务委员；中国计算机学会多值逻辑与模糊逻辑专业委员会委员.主要研究方向为计算机科学中的非经典逻辑、模糊推理算法与图像处理等，先后在国际国内专业领域的期刊上发表论文90余篇，出版专著2部，教材1部.E-mail：mxluo@cjlu.edu.cn

王雅萍 女，1990年生于甘肃兰州.硕士研究生，研究方向为非经典逻辑与模糊推理算法.

Robustness of the Reverse Triple I Algorithms Based on Schweizer-Sklar T-norms

LUO Min-xia，WANG Ya-ping

（College of Science，China JiLiang University，Hangzhou，Zhejiang 310018，China）

Since the family of Schweizer-Sklar t-norm is flexible，they have good characteristics for fuzzy reasoning based on these flexible operators.In this paper，the properties of the Schweizer-Sklar operators family and the robustness of fuzzy reasoning algorithms are studied.The family of Schweizer-Sklar t-norms are decreasing for the variable m.The family of Schweizer-Sklar t-conorms are increasing for the variable m.These perturbations of Schweizer-Sklar t-conorms，Schweizer-Sklar t-norms and its residual implications are given.We proved that Schweizer-Sklar residual implication operators（include Lukasiewizc implication operator）are more suitable in fuzzy reasoning for m∈（0，∞）.Moreover，we showed that the FMP reverse triple I algorithms based on the Schweizer-Sklar residual implications are robust for m∈（0，∞），and the FMT reverse triple I algorithms based on the Schweizer-Sklar residual implications are robust for m∈（0，∞）.

Schweizer-Sklar t-norms；reverse triple I algorithms；Minkowski distance；robustness

O142

A

0372-2112（2016）04-0959-08

电子学报URL：http：//www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.029

2014-08-25；

2015-04-05；责任编辑：孙瑶

国家自然科学基金（No.61273018）