基于深度置信网络和双谱对角切片的低截获概率雷达信号识别

2016-10-13周一鹏周东青陈忠辉田元荣

电子与信息学报 2016年11期

王星周一鹏周东青陈忠辉田元荣

王星*①周一鹏①周东青①陈忠辉②田元荣①

①(空军工程大学航空航天工程学院西安 710038)②(解放军95357部队佛山 528227)

基于深度置信网络(DBN)对信号双谱对角切片(BDS)结构特征进行学习，实现低截获概率(LPI)雷达信号识别。该方法首先建立基于受限玻尔兹曼机(RBM)的DBN模型，对LPI雷达信号的BDS数据进行逐层无监督贪心学习，然后运用后向传播(BP)机制在有监督学习方式下根据学习误差对DBN模型参数进行微调，最后基于该BDS-DBN模型实现未知信号的分类和识别。理论分析和仿真结果表明，信噪比高于8 dB时，基于BDS和DBN的识别方法对调频连续波(FMCW), Frank, Costas, FSK/PSK 4类LPI信号的综合识别率保持在93.4%以上，高于传统的主成分分析加支持向量机法(PCA-SVM)和主成分分析加线性判别分析法(PCA-LDA)。

低截获概率雷达；深度学习；深度置信网络；双谱对角切片；受限玻尔兹曼机

1 引言

低截获概率[1,2](Low Probability of Intercept, LPI)雷达信号具有时宽带宽积大、抗干扰能力强、高分辨和低截获等特性[3]，逐渐在机载火控雷达、舰载防空雷达、超视距雷达等领域广泛应用。雷达信号识别是电子对抗中的关键环节，然而传统的非合作截获接收机难以对LPI信号进行有效识别，因此LPI雷达信号的有效识别方法成为非合作雷达信号处理的研究重点。

实现雷达信号识别的关键在于选取有效的信号特征和识别算法。在信号特征选择方面，传统的脉冲描述字难以描述LPI信号等复杂的新体制雷达信号，因此模糊函数特征、熵特征、双谱特征等一系列新特征逐渐提出。其中双谱特征不仅包含了信号的振幅和相位信息，而且还具有时移不变性、尺度变化性、相位保持性以及抑制高斯噪声的特点[4]，在信号识别中具有重要优势。文献[5]通过B分离度准则提取双谱二次特征，然后基于支持向量机分类器实现雷达辐射源识别，但二次特征的提取导致部分信息丢失，影响了识别正确率的提高。文献[6]运用主成分分析方法对矩形积分双谱特征矢量降维后通过支持向量机实现对通信辐射源的识别，正确率达到90%，然而这种基于矩形积分双谱特征和通信辐射源信号特征的特征集维度较大且不完全适用于雷达信号。在识别算法方面，随着机器学习理论的发展，深度学习由于具有强大的特征学习能力，逐渐成为模式识别领域的研究热点。深度学习方法通过卷积神经网络、受限玻尔兹曼机、自编码器及其变型[7,8]等基础模块搭建深层神经网络。这类深层网络相比于神经网络算法和支持向量机等“浅层学习”方法而言，可以自动地学习得到层次化的特征表示，从而更有利于分类或特征的可视化[9]，目前已经在语音识别、信息检索和计算机视觉等领域取得了突破性进展。

在前人的研究基础上，本文提出一种基于双谱对角切片(Bispectra Diagonal Slice, BDS)和深度置信网络(Deep Belief Network, DBN)的LPI雷达信号识别方法。在信号特征方面，基于双谱的对称性提取对角切片，不仅能有效体现信号双谱特征，还可以极大地减小特征的维数；在识别算法方面，利用深度学习的强大学习和表达能力实现对BDS特征的深层次学习，进而实现LPI信号的准确识别。

2 LPI信号双谱分析

2.1双谱特征分析

双谱是信号高阶谱中三阶累量的简称，是信号三阶自相关的2维傅里叶变换。对于某LPI雷达信号()，其双谱表达式为

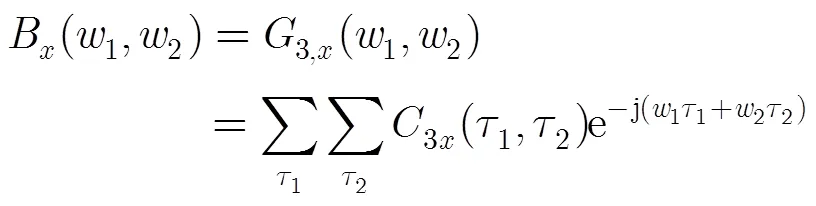
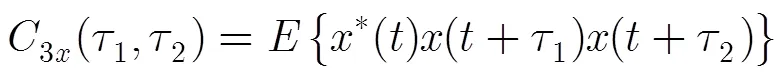
2.2 双谱对角切片(BDS)的提取

直接应用双谱进行雷达信号识别需要进行复杂的2维计算。而由于三阶自相关函数在()平面有6种对称关系，因此只要知道信号在平面内12个区域中任意一个的分布，即可根据对称性得到全平面的分布。

因此，考虑到双谱的对称特性，可选取双谱矩阵的BDS作为信号的特征，对角切片由双谱矩阵的反对角线元素组成。图2为图1中4个LPI信号样本双谱图的对角切片，4种LPI雷达信号的对角切片均关于中心对称，但切面形状区分明显，因此可以作为信号识别依据。

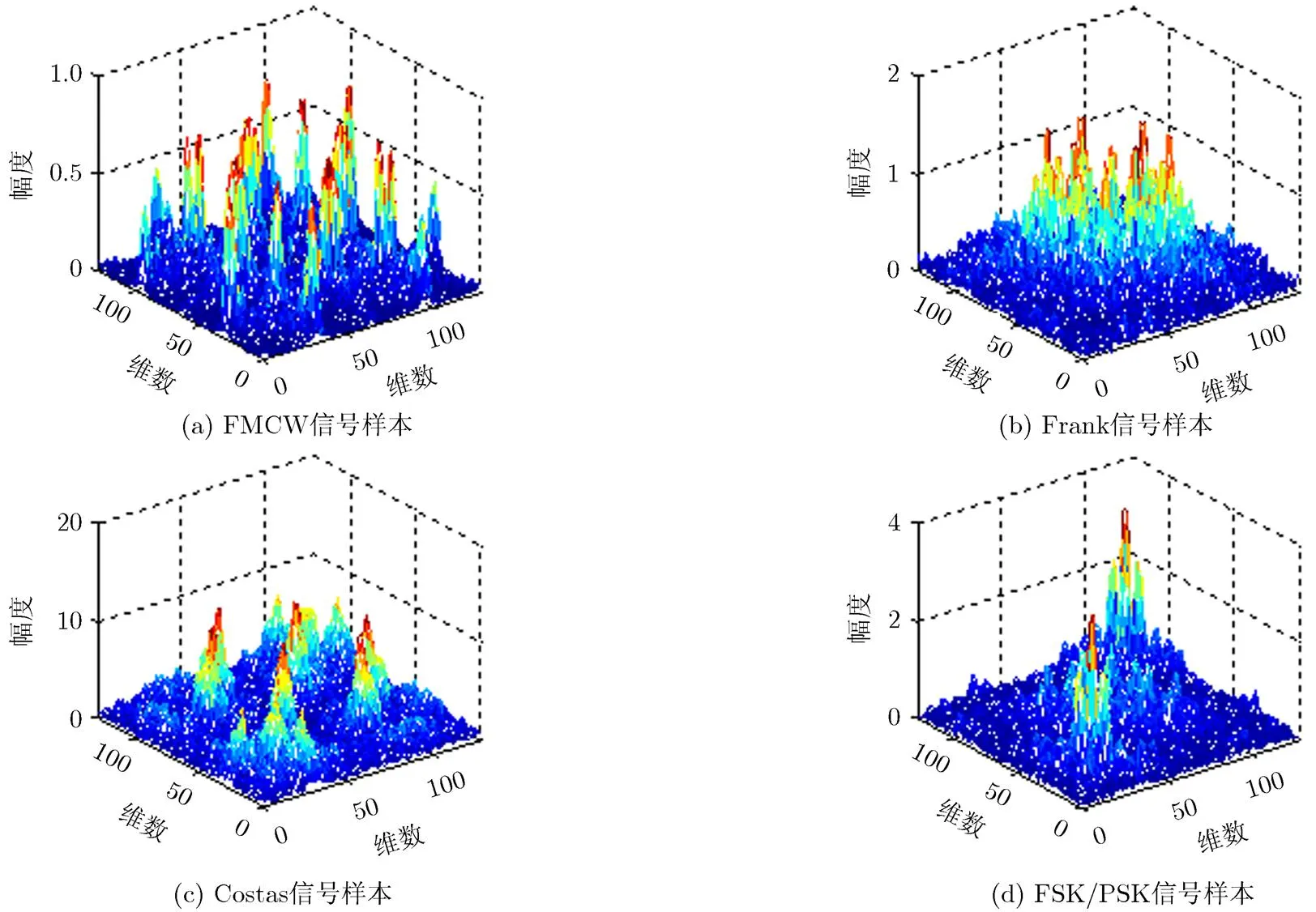
图1 4种雷达信号的双谱示例

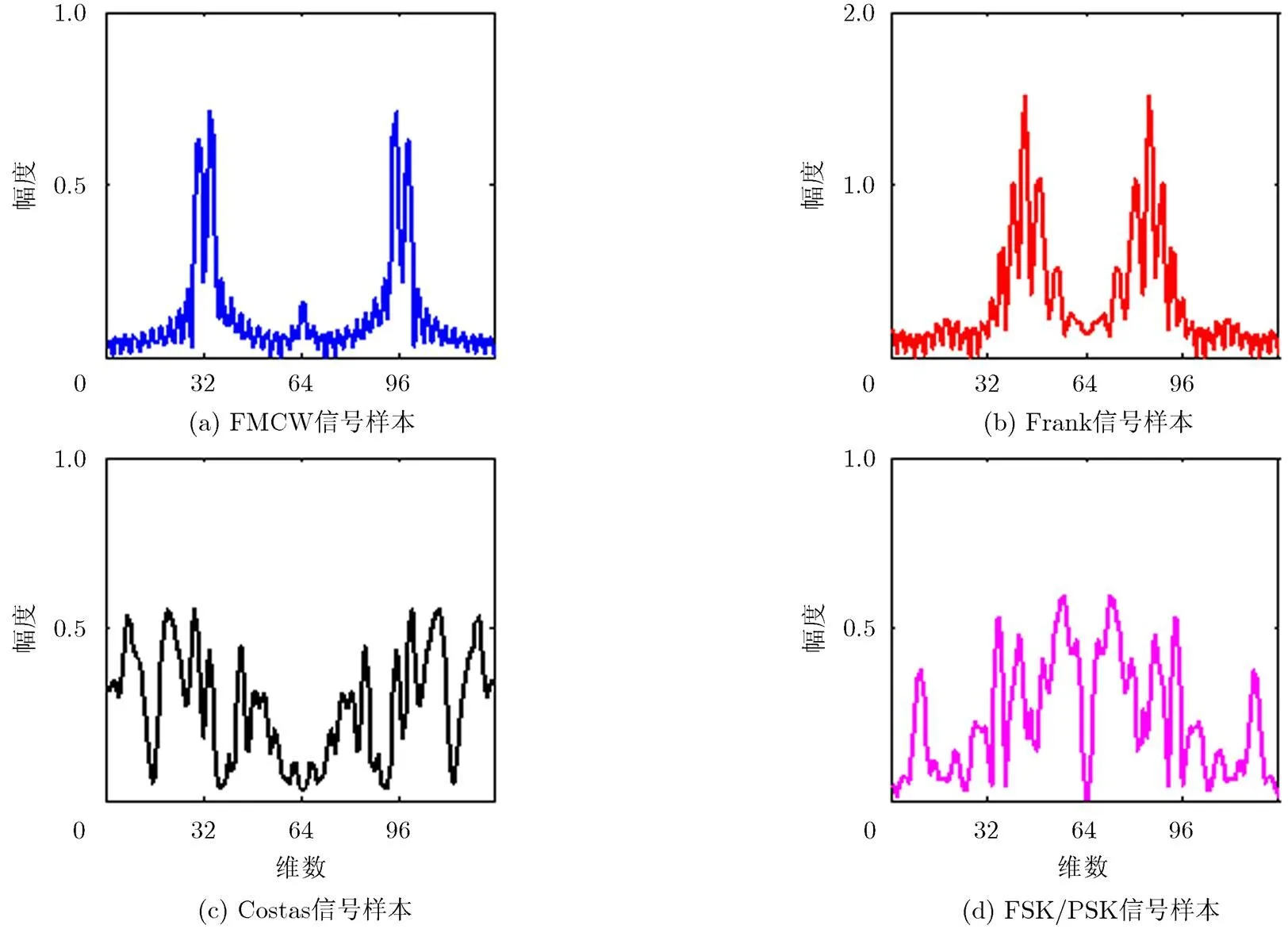
图2 4种信号BDS示例

3 基于BDS-DBN的LPI雷达信号识别

3.1受限玻尔兹曼机(RBM)预训练

DBN作为一种深层神经网络最初由Hinton等人[10]提出，这种模型可以看作是由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)前后叠加形成，是有着多层解释因子的神经网络[11,12]。RBM是DBN的基本结构单元，其网络单元分为可视层和隐含层，结构如图3所示。其中v和h取值为二值状态(取0或1)，a和b分别为对应单元的偏置值，w为单元v和h之间的权重。

图3 RBM结构示意图

单层RBM训练时，将已知的可视层数据作为输入，通过条件概率(|)得到隐含层，然后根据隐含层和条件概率(|)重构可视层。训练过程中需要调整网络参数使重构的可视层与输入的可视层之间的残差最小。当重构效果较好时可认为隐含层是可视层的一种较优的特征提取。由于提取的特征不是事先定义的，而是根据输入数字自身特点进行提取得到，因此更能体现数据内在结构特点。

3.2 基于多层RBM的DBN构建

本文算法由多个RBM构成DBN模型，以BDS作为底层RBM的输入。前一个RBM训练得到的隐含层输出作为后一个RBM的可视层输入，多个RBM逐层进行无监督贪心预训练，优化得到网络的权值组合。然后运用BP算法针对训练结果与期望结果的误差对整个网络参数进行微调。由2层RBM构成的DBN模型如图4所示，图中圆点为各层单元。

3.3 基于BDS-DBN的LPI雷达信号识别算法

在信号双谱特征和深度学习理论的基础上，本文提出一种基于BDS-DBN的LPI雷达信号识别方法。算法的具体步骤为：

步骤1 BDS提取。首先计算各类信号的双谱，然后提取其对角切片BDS，并进行归一化处理；

图4 2层RBM构成的DBN模型

步骤2 无监督的RBM训练。RBM逐层连接组成DBN模型，将训练集信号的BDS作为底层RBM的可视层输入，对各个RBM进行单独的逐层无监督贪心预训练；

步骤3 有监督的BP微调。在最后一个RBM的输出后加上一个后向传播(Back Propagation, BP)机制用于有监督的学习。即将带类别标签的BDS数据作为输入，运用BP算法将实际分类结果和样本标签的误差向后逐层传递，对整个DBN网络进行参数微调以降低误差，并将DBN模型参数传递给分类层；

步骤4 信号识别。将测试集样本的BDS作为模型输入，进行信号识别。

4 实验结果及分析

4.1实验设置

实验所使用的LPI信号均通过Low Probability of Intercept Toolbox[13]产生，包括4种LPI信号：调频连续波(Frequency Modulation Continuous Wave, FMCW)信号，Frank信号，Costas信号和FSK/PSK信号。

FMCW信号：采用三角波FMCW波形，载频0范围为1~2 kHz，采样频率f1为7 kHz，调制带宽范围为250~350 Hz; Frank信号：采用8个步进频率，载频0范围为1~2 kHz，采样频率f2为7 kHz; Costas信号：频率序列为[3 2 6 4 5 1] kHz和[2 4 8 5 10 9 7 3 6 1] kHz，频率波动范围为500 Hz，采样频率f3为15 kHz; FSK/PSK信号：基于Costas序列跳频的FSK信号和PSK信号组合，跳频序列为[5 4 6 2 3 1] kHz, 频率波动范围为500 Hz，采样频率f4为15 kHz。4种信号的幅度均为1，长度为500，各产生信号样本的BDS共500组，有监督预训练时随机选择每类信号的250组作为训练集，将剩下的250组作为测试集。

双谱运算采用非参数化直接双谱估计法[14]，获得的双谱矩阵为128128维，BDS为1128维。DBN网络的深度为2层，为了保证对原始数据的全信息输入，底层RBM的可视层单元数设为128，隐含层单元数为80，第2层RBM的隐含层单元数为60。

4.2结果及分析

4.2.1算法识别效果为了验证BDS在雷达信号识别中的有效性，将BDS-DBN算法与直接利用DBN识别原始信号的算法进行比较，识别效果如表1所示。

由表1可知，采用BDS作为DBN输入比采用原始信号直接作为输入的识别率有显著提高，说明BDS能够作为区分不同LPI雷达信号的有效特征。

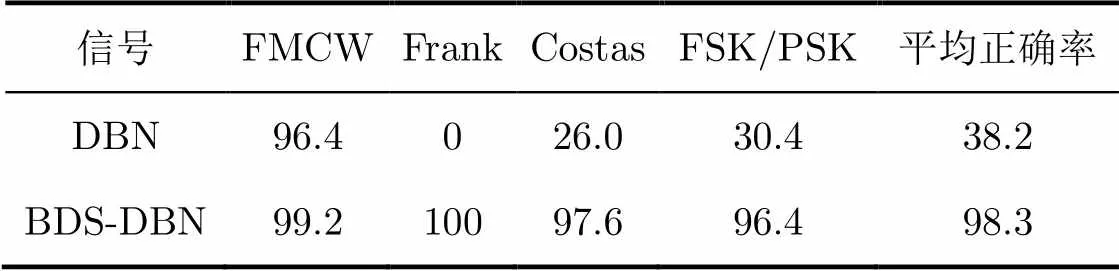
表1 DBN与BDS-DBN识别正确率对比(%)

进一步分析BDS-DBN算法中各层的输出特性。通过LDA方法将4种信号在各层的输出降维到1,2和3组成的3维空间。图5(a)-图5(c)分别为原始信号、底层RBM输出以及第2层RBM的降维输出。从图5(a)中可知4种信号的原始数据在降维空间中严重混叠。随着RBM个数的增加，从底层RBM输出和第2层RBM输出可以看出4种信号样本逐渐分离。上述现象说明本文采用的DBN模型能够对4种信号进行逐层有效分离。

4.2.2不同算法识别效果比较将本文提出的BDS- DBN算法与PCA-LDA算法以及PCA-SVM算法进行比较，在不同加性高斯白噪声条件下对4类LPI信号进行识别，识别结果如表2所示。

表2不同信噪比下的识别正确率(%)

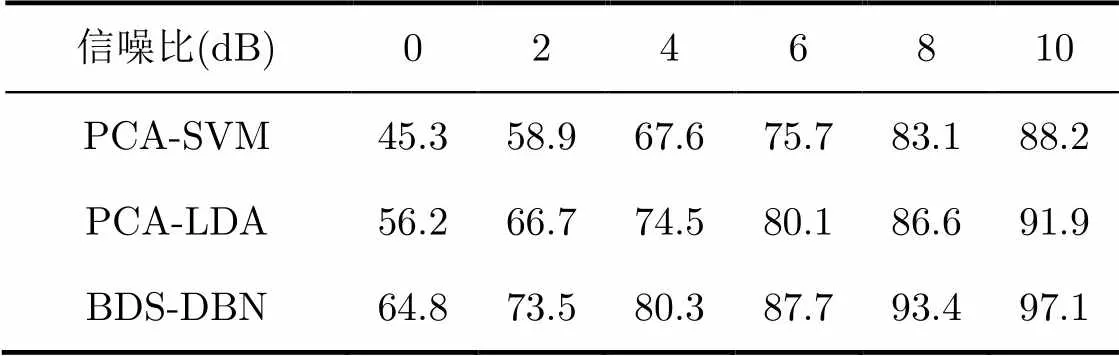
信噪比(dB)0246810 PCA-SVM45.358.967.675.783.188.2 PCA-LDA56.266.774.580.186.691.9 BDS-DBN64.873.580.387.793.497.1

表2中可以看出，在不同信噪比条件下本文算法的识别正确率均高于PCA-LDA算法和PCA- SVM算法。由于PCA-LDA算法基于线性降维后最大化类间距离并最小化类内距离的思想，因此对于数据样本的特征学习不充分；而SVM算法作为一种浅层学习方法，对于信号双谱特征这类高度非线性数据学习能力较差；相比之下BDS-DBN算法通过RBM单元对数据内在特征进行降维和特征提取，对BDS数据的内在结构学习更充分，因而对于4类LPI雷达信号的识别更有效。

5 结束语

本文提出一种基于信号双谱对角切片特征和深度置信网络的LPI雷达信号识别算法。在信号特征提取方面，基于信号双谱特性提出的BDS特征拓展了雷达对抗侦察中的信息维度，可以有效地表征雷达信号特征；在识别方法方面，基于BDS和DBN的LPI雷达信号识别方法可以获得良好的识别正确率。仿真结果表明，在不同信噪比条件下，该算法可以有效识别典型的LPI雷达信号，识别性能优于传统的PCA-SVM和PCA-LDA算法。

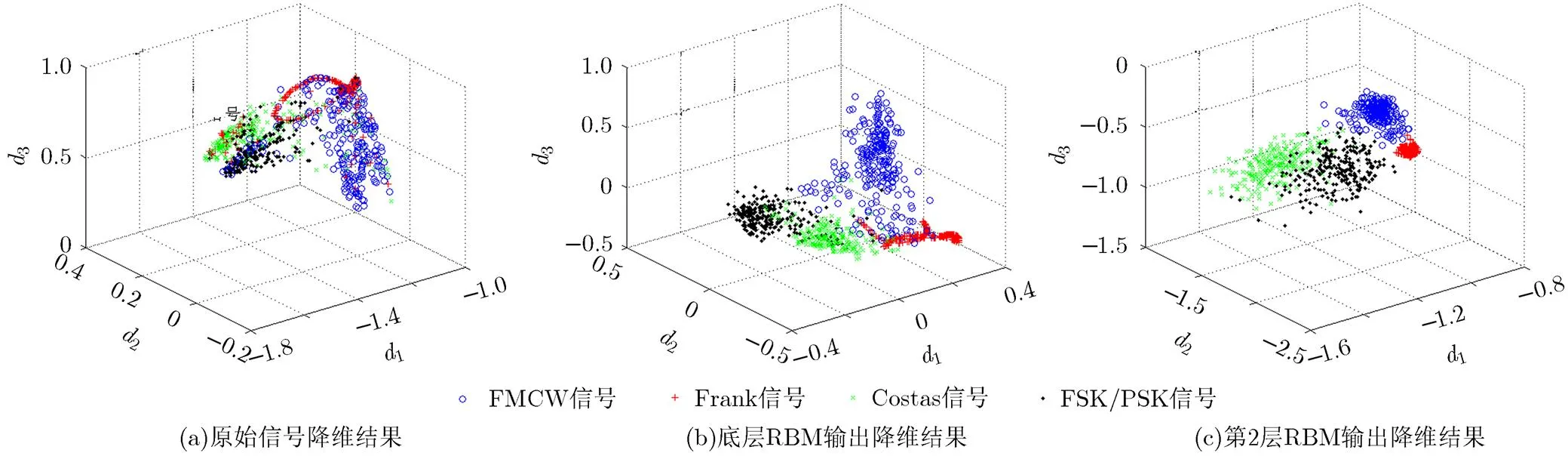
图5 DBN模型中各层输出的降维结果

[1] PHILLIP E P. Detecting and Classing Low Probability of Intercept Radar (Second Edition)[M]. Norwood, MA, USA, Artech House, 2009: 1-15.

[2] LIU Y J, XIAO P, WU H C,. LPI radar signal detection based on radial integration of Choi-Williams time-frequency image[J]., 2015, 26(5): 973-981. doi: 10.1109/JSEE.2015.00106.

[3] 李娜, 王珂, 李保珠. 低截获概率雷达信号检测方法的优化及应用[J]. 光学精密工程, 2014, 22(11): 3122-3128. doi: 10. 3788/OPE. 20142211.3122.

LI Na, WANG Ke, and LI Baozhu. Optimization and application of LPI radar signal detection method[J]., 2014, 22(11): 3122-3128. doi: 10.3788/OPE. 20142211.3122.

[4] 蔡忠伟, 李建东. 基于双谱的通信辐射源个体识别[J]. 通信学报, 2006, 28(2): 75-79. doi: 10.3321/j.issn:1000-436x.2007.02. 012.

CAI Zhongwei and LI Jiandong. Study of transmitter individual identification based on bispectra[J]., 2006, 28(2): 75-79. doi: 10.3321/j.issn: 1000-436x.2007.02.012.

[5] 王世强, 张登福, 毕笃彦, 等. 双谱二次特征在雷达信号识别中的应用[J]. 西安电子科技大学学报(自然科学版), 2012, 39(2): 127-132. doi: 10.3969/j.issn.1001-2400.2012.02.021.

WANG Shiqiang, ZHANG Dengfu, BI Duyan,. Research on recognizing the radar signal using the bispectrum cascade feature[J]., 2012, 39(2): 127-132. doi: 10.3969/j.issn.1001-2400.2012.02.021.

[6] 徐书华, 黄本雄, 徐丽娜. 基于SIB/PCA的通信辐射源个体识别[J]. 华中科技大学学报(自然科学版), 2008, 36(7): 14-17. doi: 10.3321/j.issn:1671-4512.2008.07.004.

XU Shuhua, HUANG Benxiong, and XU Lina. Identification of individual radio transmitters using SIB/PCA[J].(), 2008, 36(7): 14-17. doi: 10.3321/j.issn:1671- 4512.2008.07.004.

[7] 胡振, 傅昆, 张长水. 基于深度学习的作曲家分类问题[J] . 计算机研究与发展, 2014, 51(9): 1945-1954. doi: 10.7544/issn. 1000-1239.2014.20140189.

HU Zhen, FU Kun, and ZHANG Changshui. Audio classical composer identification by deep neural network[J]., 2014, 51(9): 1945-1954. doi: 10.7544/issn.1000-1239.2014.20140189.

[8] SCHMIDHUBER J. Deep learning in neural networks: An overview[J]., 2014, 61: 85-117. doi: 10.1016/ j.neunet.2014.09.003.

[9] 尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015, 41(1): 48-59. doi: 10.11936/bjutxb2014100026.

YIN Baocai, WANG Wentong, and WANG Lichun. Review of deep learning[J]., 2015, 41(1): 48-59. doi: 10.11936/bjutxb2014100026.

[10] HINTON G E, OSINDERO S, and TEH Y W. A fast learning algorithm for deep belief nets[J]., 2006, 18(7): 1527-1554.doi: 10.1162/neco.2006.18.7.1527.

[11] SARIKAYA R, HINTON G E, and DEORAS A. Application of deep belief networks for natural language understanding[J].,,, 2014, 22(4): 778-784. doi: 10.1109/TASLP. 2014.2303296.

[12] HINTON G, LI D, DONG Y,. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups[J]., 2012, 29(6): 82-97. doi: 10.1109/MSP.2012.2205597.

[13] TABOADA and FERNANDO L. Detection and classification of low probability of intercept radar signals using parallel filter arrays and higher order statistics[D]. [Ph.D. dissertation], Naval Postgraduate School, 2002.

[14] 张旭. 基于信号分析的无线设备“指纹”特征提取[D]. [硕士论文], 北京邮电大学, 2014: 13-14.

ZHANG Xu. Wireless devices “fingerprint” feature extraction based on signal analysis[D]. [Master dissertation], Beijing University of Posts and Telecommunications, 2014: 13-14.

Research on Low Probability of Intercept Radar Signal Recognition Using Deep Belief Network and Bispectra Diagonal Slice

WANG Xing①ZHOU Yipeng①ZHOU Dongqing①CHEN Zhonghui②TIAN Yuanrong①

①(,,’710038,)②(95357,528227,)

A novel recognition algorithm for Low Probability of Intercept (LPI) radar signal based on deep learning of radar signals’ Bispectra Diagonal Slice (BDS) is proposed in this paper. Firstly, a Deep Belief Network (DBN) model is established on stacked Restricted Boltzmann Machines (RBM), then the model is used for layer-by-layer unsupervised greedy learning of radar signals’ BDS. Secondly, a Back Propagation (BP) algorithm is applied to fine tune parameters of DBN model with a supervised way according to learning error. Finally, the BDS-DBN model is constructed to classify and recognize unknown LPI signals. The theoretical analysis and the simulation results show that, the average recognition accuracy of the proposed algorithm for Frequency Modulation Continuous Wave (FMCW), Frank, Costas and FSK/PSK signals can reach 93.4% or ever higher while the SNR is better than 8 dB, which is better than that of Principal Component Analysis-Support Vector Machine (PCA-SVM) algorithm and Principal Component Analysis-Linear Discriminant Analysis (PCA-LDA) algorithm.

Low Probability of Intercept (LPI) radar; Deep learning; Deep Belief Network (DBN); Bispectra Diagonal Slice (BDS); Restricted Boltzmann Machine (RBM)

TN97

1009-5896(2016)11-2972-05

10.11999/JEIT160031

2016-01-16；改回日期：2016-07-14；

2016-09-30

王星 wang_xing1965@163.com

国家自然科学基金(61372167)，航空科学基金(20152096019)

The National Natural Science Foundation of China (61372167), The Aeronautical Science Foundation of China (20152096019)

王星：男，1965年生，教授，博士生导师，研究方向为电子对抗理论与技术.

周一鹏：男，1992年生，硕士生，研究方向为电子战信号处理.

周东青：男，1988年生，博士生，研究方向为组网电子对抗.

陈忠辉：男，1969年生，高级工程师，研究方向为电子对抗理论与技术.